Linex损失函数下Laplace分布尺度参数的Bayes估计

王瑞鸿, 徐 宝

(吉林师范大学 数学学院, 吉林 四平 136000)

Laplace分布是常见的连续型概率分布，也叫作双指数分布，具有重尾特征。该分布在证劵金融经济领域、语音辨识、图像压缩过程、工程测绘数据的处理等实际问题中有着重要的应用[1]。

Laplace分布定义：若随机变量X的密度函数为

(1)

则称随机变量X服从Laplace(μ,σ)分布，μ为位置参数，σ为尺度参数，σ>0，且记作X～La(μ,σ)。由Laplace密度函数能够得到其分布函数为

(2)

在位置参数μ已知时，从Laplace分布中抽取容量为n的简单样本X1,X2,X3,…Xn，记X=(X1,X2,X3,…Xn),x=(x1,x2,x3…xn)为X的观察值。

Linex损失函数也称为线性指数损失函数，其损失是非对称的。该损失函数自提出以来，学者们将它应用于参数的统计研究。

Linex损失函数其形式为：

L(δ,h(θ))=b{ec[h(θ)-δ]-c[h(θ)-δ]-1},(c≠0,b>0)

式中：h(θ)是δ的估计;c、b分别为尺度参数和形状参数，简写为

(3)

本文仅考虑c>0的情形。

文献[2]研究了以倒伽马分布为共轭先验分布的Laplace分布参数θ的估计和风险函数，并进行了实例分析。文献[3]研究了构造一类损失函数，具有较好的去躁效果，导出多元Laplace分布的方差、协方差等。文献[4]研究Laplace分布的主要性质和各个分布相互之间的联系以及拟合优度检验。文献[5]讨论了2种不同先验信息分布下，二项分布参数θ的3种类别的贝叶斯估计。王学敏等[6，7]探讨了Linex损失的发展，在Gamma分布为共轭先验分布时，对Poisson分布和Burr分布求出参数的Bayes估计的可容许性和多层Bayes估计。其他学者也对不同的损失函数针对不同分布函数进行研究，并对其中参数进行相关的Bayes估计等[8-11]。

参数估计的优劣水平大部分取决于损失函数的抉择。选取不同的损失函数，估计量的不同，优良性也会产生差别。本文在Linex损失函数下，当Laplace分布中位置参数已知时，在不同的先验分布下，研究尺度参数的Bayes估计形式与性质。

1 尺度参数的Bayes估计

在Linex损失函数下，研究Laplace分布尺度参数的Bayes估计的形式。

定理1 在Linex损失函数下，对任意先验分布，Laplace分布尺度参数θ的Bayes估计为

证明：设Linex损失函数为

则决策函数的Bayes风险为

(4)

要使Bayes估计最小，则需要使Bayes风险最小，即E(P)取最小值，通过求导等于零，推出参数θ的Bayes估计为

(5)

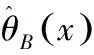
当该分布处于无先验信息时，设样本来自Laplace分布，在Linex损失下，以定理的方式给出关于参数的Bayes估计。

定理2 在Linex损失函数下，设样本来自Laplace分布，取参数θ=(μ,σ)的无信息先验分布，则参数θ的Bayes估计为

证明：参数θ=(μ,σ)的对数似然函数为

(6)

其Fisher信息阵为

I(θ)=(Iij(θ))2×2

(7)

(8)

(9)

(10)

(11)

(12)

θ的无信息先验密度为

(13)

则在Linex损失函数下，参数θ=(μ,σ)的Bayes的估计为

(14)

当分布的共轭先验分布为倒伽马分布时，设样本来自Laplace分布，在Linex损失下，以定理的方式给出关于参数的Bayes估计。

2 尺度参数的Bayes估计的性质

定理3 在Linex损失函数下，设X1,X2,X3,…Xn是来自Laplace分布的一个简单随机变量，取参数σ的共轭先验分布为ΙΓ(α,β)，则

(1)参数σ的唯一Bayes估计为

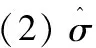
给定来自Laplace分布的样本X=(X1,X2,X3,…Xn)，则σ后验概率密度为

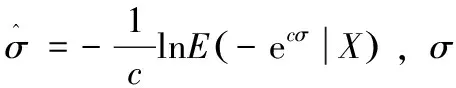
从而

(15)

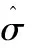
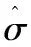
3 结 语

利用Linex损失函数质，研讨了Laplace分布中的尺度参数基于不同先验分布下的Bayes估计的形式。当Laplace分布处于无信息分布时，通过求Fisher信息阵和它的后验密度，推出其Bayes估计；当Laplace分布取共轭先验分布为ΙΓ(α,β)时，推测其Bayes估计的唯一性及其可容许性。在现有信息的基础上丰富了Laplace分布的参数估计，将Linex损失函数应用更加宽泛。