铠装热电偶动态响应校准过程数值研究

刘 波，郑 伟，王志远，李雪菁

(1. 上海市计量测试技术研究院，上海 201203；2.上海理工大学 能源与动力工程学院，上海 200093)

1 引 言

温度传感器的热响应时间描述其对阶跃温度的响应，对于可近似为一阶系统的温度传感器，其输出温度变化达到阶跃量的63.2%所需要的时间称为时间常数。时间常数是影响动态温度测量准确性的重要参数，也是衡量温度传感器动态响应性能的重要指标。由于影响时间常数的因素较多且复杂，通常需要实验来测量[1,2]。

温度传感器动态响应校准装置包括：产生稳定温度场、速度场的恒温恒速系统，使温度传感器接受激励的温度阶跃系统，采集被校传感器响应信号的测试系统。时间常数是一个多影响量参数，与传感器的密度、比热容、导热、体积、表面积以及传感器与温场介质间的换热系数等参数有关。传感器动态响应校准应尽量与传感器工作条件一致。贾超等[3]研究了传热方式对温度传感器动态特性的影响，采用油浴法和激光法对热电偶时间常数进行测试；杨兆欣等[4]在气体温度动态校准装置中实验验证了一种热电偶级联系统动态性能评估方法；刘波等[5,6]针对核电快响应温度计，研制了水流环境温度传感器动态响应校准装置，并开展了不确定度评估；白鸽[7]对航空发动机进气总温传感器开展了热风洞试验，形成了某型传感器的气流马赫数与响应时间的关系曲线。温度传感器动态响应校准的方法和装置也用于动态温度测量误差分析和不确定度评定[8,9]。

温度传感器动态响应实验室校准装置通常难以实现与传感器实际使用一致的条件，基于有限元或有限体积法的数值仿真技术逐步应用在温度传感器动态响应校准中，可模拟更宽的实验条件，节省大量实验时间和成本。Coote等[10]使用Ansys Mechanical软件模拟了光纤温度传感器在光脉冲加热和温度阶跃输入两种情况下的时间常数，结果均为ms级；Luo等[11]采用有限元法分析了不同封装材料(空气、油脂、铜)光纤温度传感器在正、负温度阶跃激励下的时间常数；张磊等[12]使用FloEFD软件仿真分析了不同设计方案下镍电阻温度传感器的动态响应，优选了填充材料、骨架材料、骨架形状等参数。

回路电流阶跃响应(loop current step response，LCSR)法用于在役运行条件下温度计响应时间的原位测量。宋延勇[13]建立了LCSR法电阻温度计响应时间原位测量装置，在装置上验证了阶跃电流和换热条件对响应时间的影响。

热电偶因响应快速而得到广泛应用，本文采用数值仿真技术研究了铠装热电偶的动态响应校准过程。首先建立了铠装热电偶的三维结构模型，进行了网格划分和网格无关解验证；其次分析了绝缘层MgO不同填充密实度下插入法和回路电流阶跃法获得的热电偶动态响应曲线，对LCSR法响应数据进行拟合、变换分析，比较了2种校准方法获得时间常数的偏差。

2 热电偶结构与网格划分

图1为铠装热电偶的剖面结构图，热电偶的直径设为D，铠装套管的壁厚设为0.1D。为方便计算，设置正负极偶丝的直径相同，均为0.2D。

图2为铠装热电偶三维网格划分示意图，由于测量端的结构复杂，采用适应性良好的四面体网格划分；电缆延伸段为规则的柱体，采用规则六面体网格划分，以减少网格数量、节省计算时间。取D=6 mm进行计算。

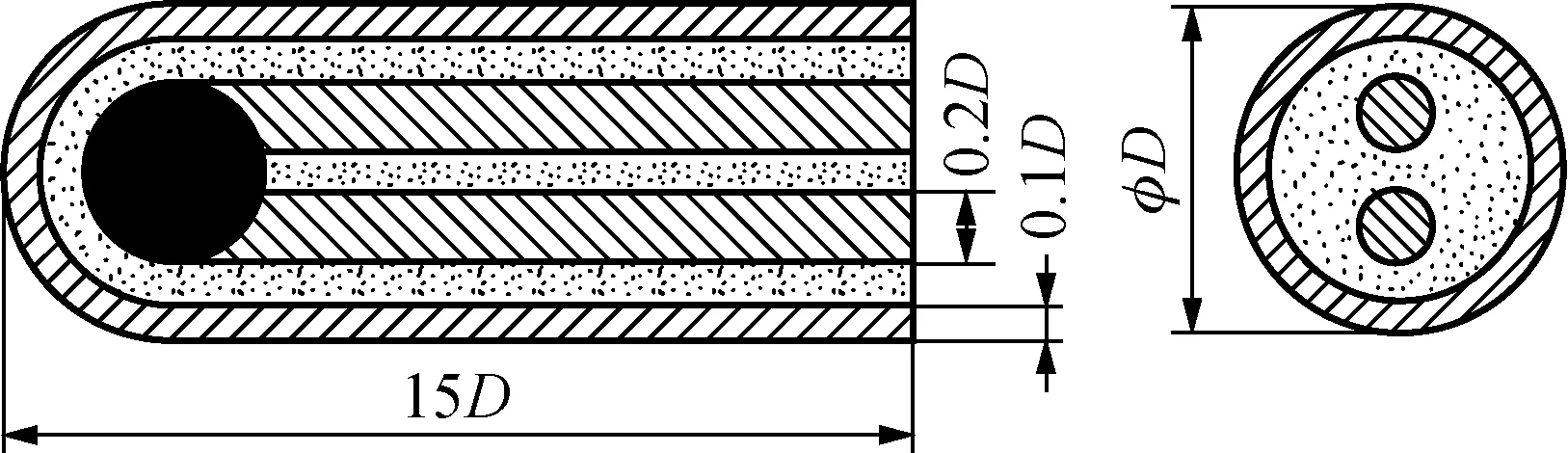
图1 铠装热电偶剖面结构示意图Fig.1 Cross section of the sheathed thermocouple

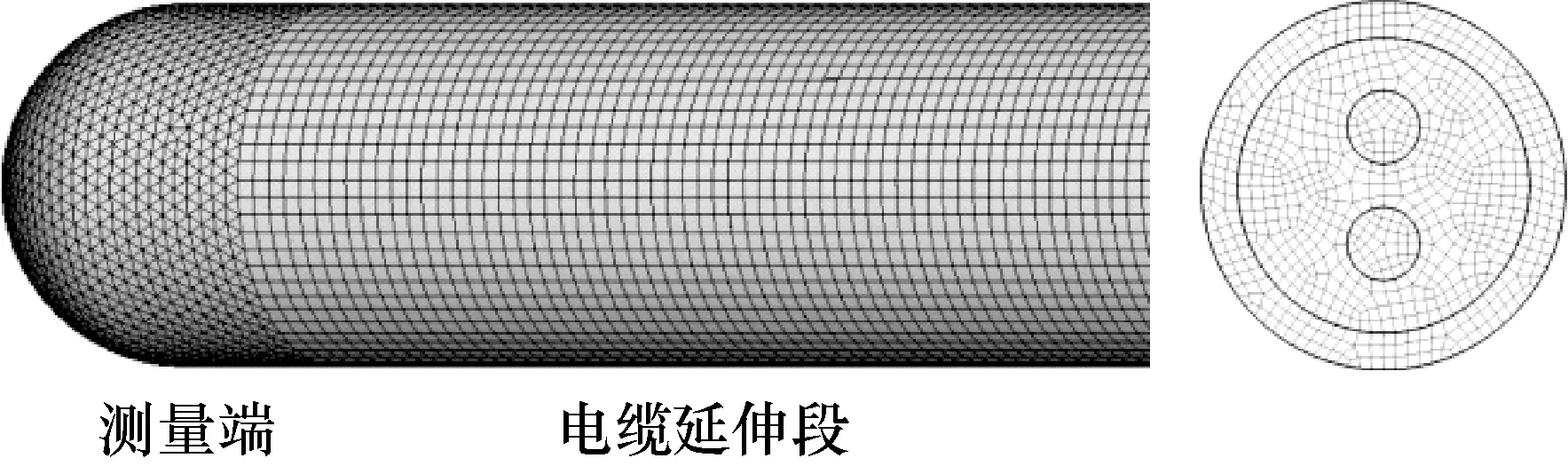
图2 铠装热电偶三维网格划分示意图Fig.2 Three-dimensional mesh of the sheathed thermocouple

3 实验设计

以K型铠装热电偶为例，保护管为SUS304不锈钢，绝缘层填充MgO粉，热电极为镍铬/镍硅合金， 300 K时材料的热物性参数见表1[14]。热电偶丝焊接点近似为正极Ni-Cr10材料，以焊接点的平均温度作为热电偶输出温度。

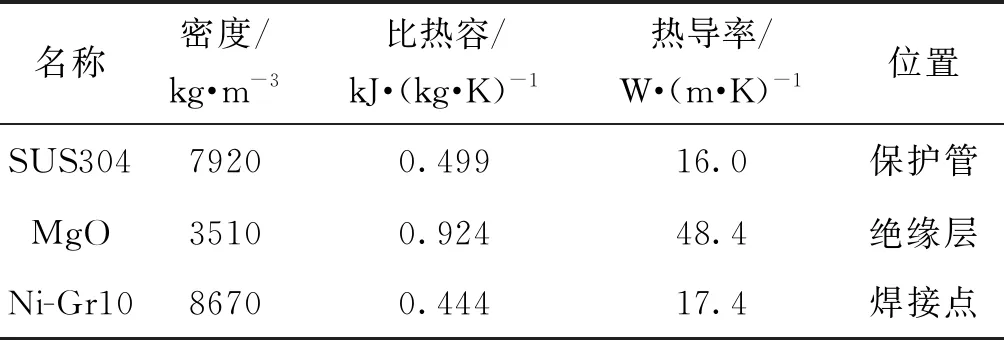
表1 铠装热电偶材料热物性参数Tab.1 Thermophysical parameters of the sheathed thermocouple materials

换热系数是影响温度传感器热响应时间的重要参数。在掷入法温度传感器动态响应校准过程中，模拟环境温度为300 K，阶跃温度为50 K，该过程可认为是横向流动中圆柱体的强制对流换热，根据Zukauskas关系式[15]，以阶跃过程的中间温度325 K作为热电偶的等效温度，计算得到水流速1 m/s下的对流换热系数为11 851 W/(m2·K)。在LCSR法中，电流通过热电偶丝产生焦耳热，热电偶焊接点温度升高，通过对测得的温度响应数据拟合、变换以计算时间常数。对热电偶焊接点施加热功率0.09 W，能量密度为7.0×106W/m3，焊接点产生的温升小于0.5 K，模拟LCSR法温度传感器动态响应校准过程，计算得到水流速1 m/s时对流换热系数为13 101 W/(m2·K)。

绝缘层MgO粉填充的密实程度对绝缘层的密度、比热容和热导率产生影响，进而影响热电偶的时间常数。绝缘层的密度为MgO粉和空气密度的加权算数平均值，加权系数为MgO粉和空气的体积百分数，MgO粉的体积百分数定义为填充密实度r。MgO粉的比热容值0.924 kJ/(kg·K)与空气101.325 kPa下的定压比热容值1.006 6 kJ/(kg·K)较接近，绝缘层的比热容值按照MgO粉和空气的体积百分数加权算数平均的方法计算。绝缘层属于固相和气相混合而成的两相材料，其热导率不仅与组成相的热导率、相对体积分数，还与每相的分布、排列、取向有关。对于固相颗粒分散在流体中的情形，复合热导率可用Maxwell公式[14]近似计算。不同填充密实度r下绝缘层的热物性参数如表2所示。

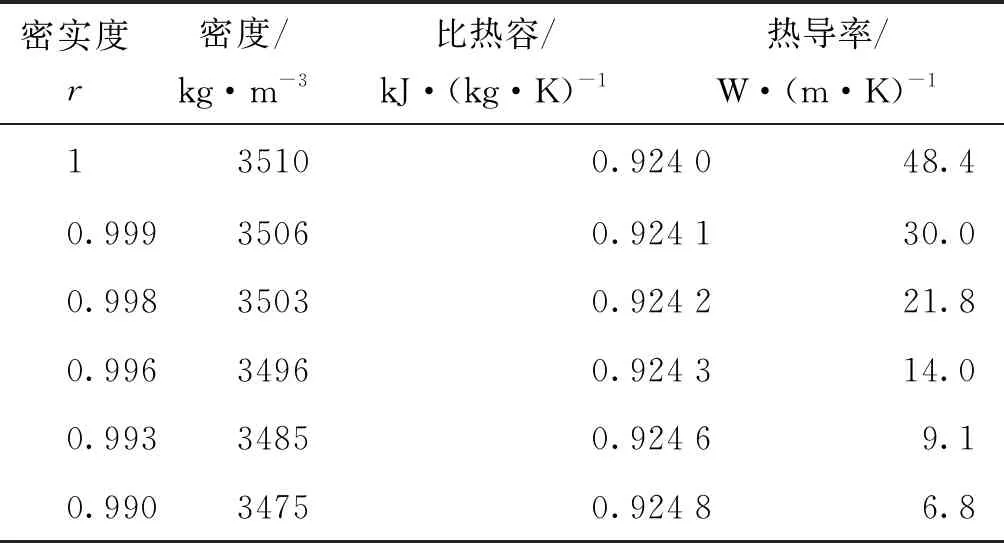
表2 不同MgO填充密实度下绝缘层的热物性参数Tab.2 Thermophysical parameters of the insulating layer with MgO filling ratio

4 数学模型和网格、浸没深度验证

基于有限体积法进行铠装热电偶区域离散化，采用二阶迎风格式对能量方程进行离散，采用基于单元格的最小二乘法差值对梯度方程进行离散。控制方程的离散和求解为通用设置，本文不再赘述。数值仿真在计算流体力学软件Fluent中进行。

本文模型的能量方程不涉及对流和辐射传热，仅求解导热形式：

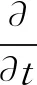
(1)

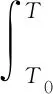
(2)

式中:h为离散单元体物质的焓;λ为热导率;c为比热容;T0为参考温度取298.15 K;Sh表示热源，在插入法中，Sh为0,在LCSR法中，Sh为向热电偶施加的热功率。

基于三维瞬态算法求解模型，每时间步计算的能量方程残差小于10-8，总测试时间不少于20倍时间常数。采用可变时间步长，在阶跃初期热电偶焊接点温度变化速率大，时间步长为0.001 s；在阶跃后期热电偶焊接点温度变化速率小，逐渐接近水流温度，时间步长为0.05 s。

为选取合适的网格大小，在保证计算精度的条件下节省计算时间，在水流速v=1 m/s条件下，对掷入法温度传感器动态响应校准过程进行数值仿真。分别以0.2、0.25、0.3和0.35 mm为主要尺寸对图1所示的铠装热电偶进行网格划分，分别获得444 946、258 867、142 484和96 845个网格单元体。

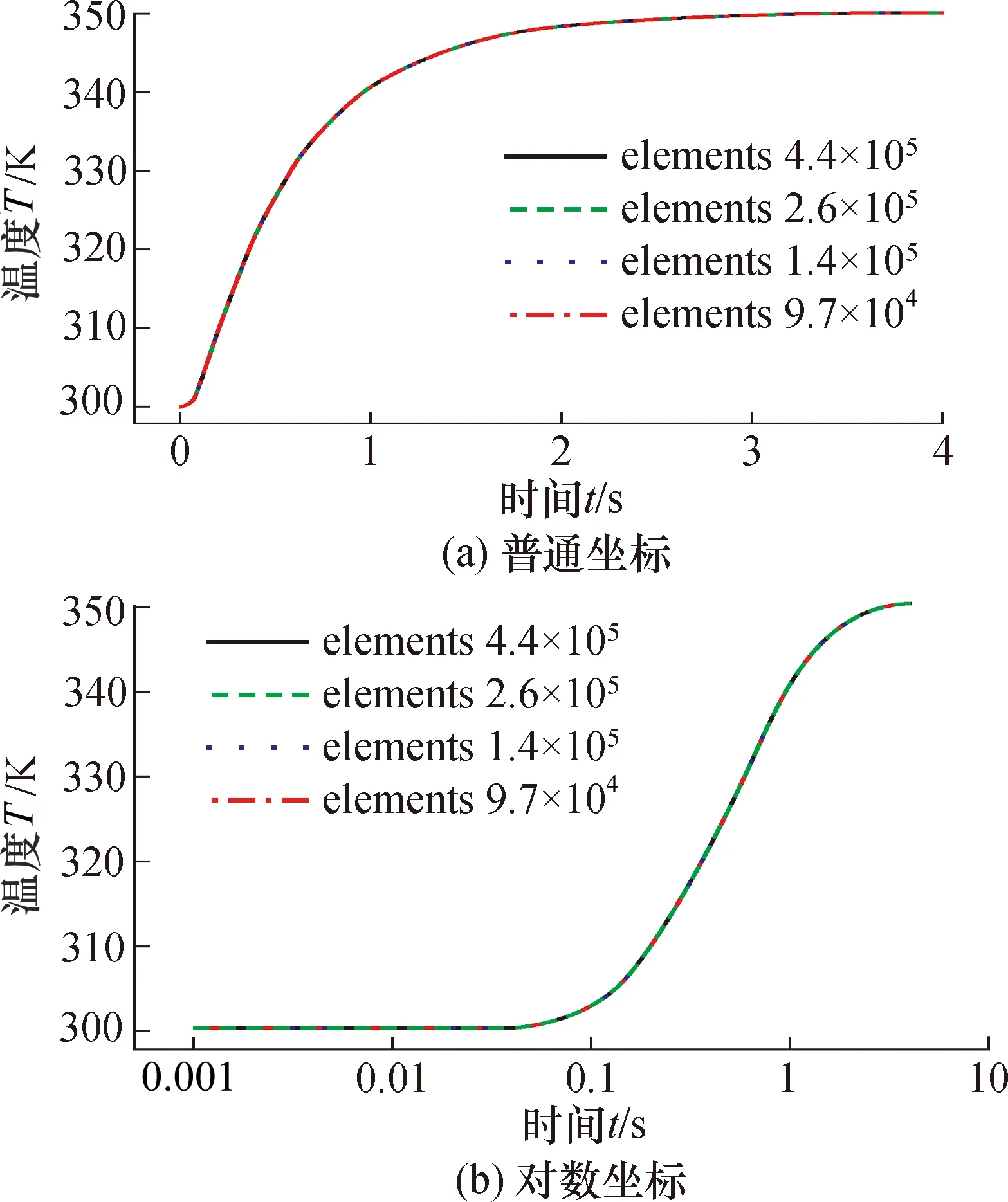
图3 网格数量对铠装热电偶动态响应的影响Fig.3 Effect of elements on the dynamic response of the sheathed thermocouple

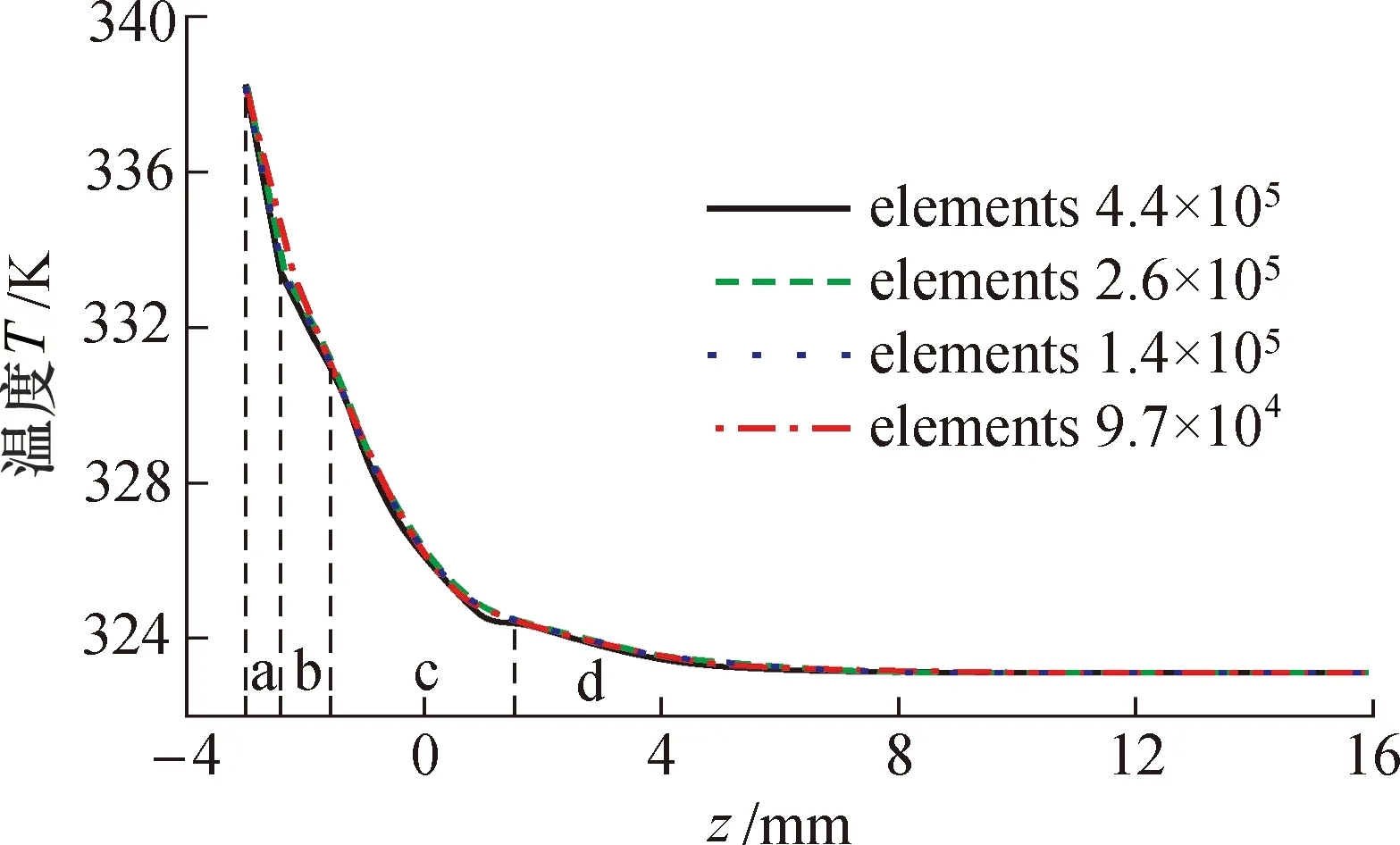
图4 网格数量对铠装热电偶轴向温度分布的影响(时间t=0.5 s)Fig.4 Effect of elements on the z axis temperature distribution of the sheathed thermocouple (time t=0.5 s)

不同网格数量对热电偶动态响应仿真结果的影响如图3所示，图3(a)和图3(b)分别为普通坐标和对数坐标下显示的结果。由图可知，4种网格数量下的温度动态响应曲线几乎完全重合，说明4种网格数量对热电偶动态响应计算结果的影响不明显。为进一步分析网格数量对数值仿真过程的影响，在时间0.5 s时对比了z轴的温度分布，如图4所示，4种网格数量下的温度分布曲线基本重合。图4中a、b、c、d 4个区域分别对应铠装热电偶z轴上的不锈钢保护管层、绝缘MgO层、焊接点和绝缘MgO层，由图可知，在每层交界附近，由于材料热物性的突变，导致温度曲线斜率存在明显的变化。基于图3和图4结果的分析，本文数值研究选用0.3 mm为主要尺寸的网格划分方式，既能保证计算精度，又能节省计算时间。

为消除热电偶电缆延伸段轴向漏热对测量结果的影响，其末端横截面设为绝热壁面；并参照温度传感器允差校准时对浸没深度的要求，设置热电偶的浸没深度为15D。本文开展了浸没深度分别为5D、10D、15D和20D条件下的数值仿真，结果显示4种浸没深度下温度动态响应曲线几乎完全重合，求得热电偶的时间常数为0.627～0.630 s，相对变化小于0.5%，说明边界条件和浸没深度设置合理。

5 结果分析与讨论

插入法获得的不同填充密实度r对热电偶动态响应曲线的影响如图5所示，图中热响应曲线具有相似的形状，随着填充密实度的减小，热电偶绝缘层的热导率降低，导致温度响应曲线变缓，时间常数增大。图6所示为r=0.996时，插入法和LCSR法获得的热电偶动态响应曲线。为便于比较响应曲线的变化，对温度响应数据进行了归一化处理。在局部放大图中，由于热电偶保护管和绝缘层的热惯性，插入法获得的温度动态响应曲线在起始时刻后的一段时间内变化不明显，该段时间称为“延迟时间”(deadtime)。由于LCSR法直接使焊接点感温层产生热量，因而在起始阶段不存在延迟时间。

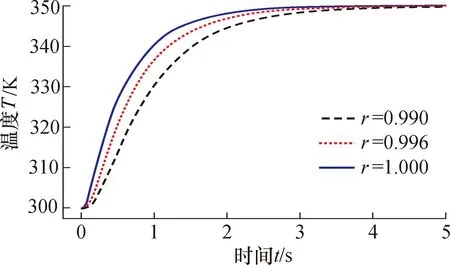
图5 填充密实度r对热电偶动态响应的影响(插入法)Fig.5 Effect of MgO ratio on the dynamic response of the thermocouple (by plunge test)

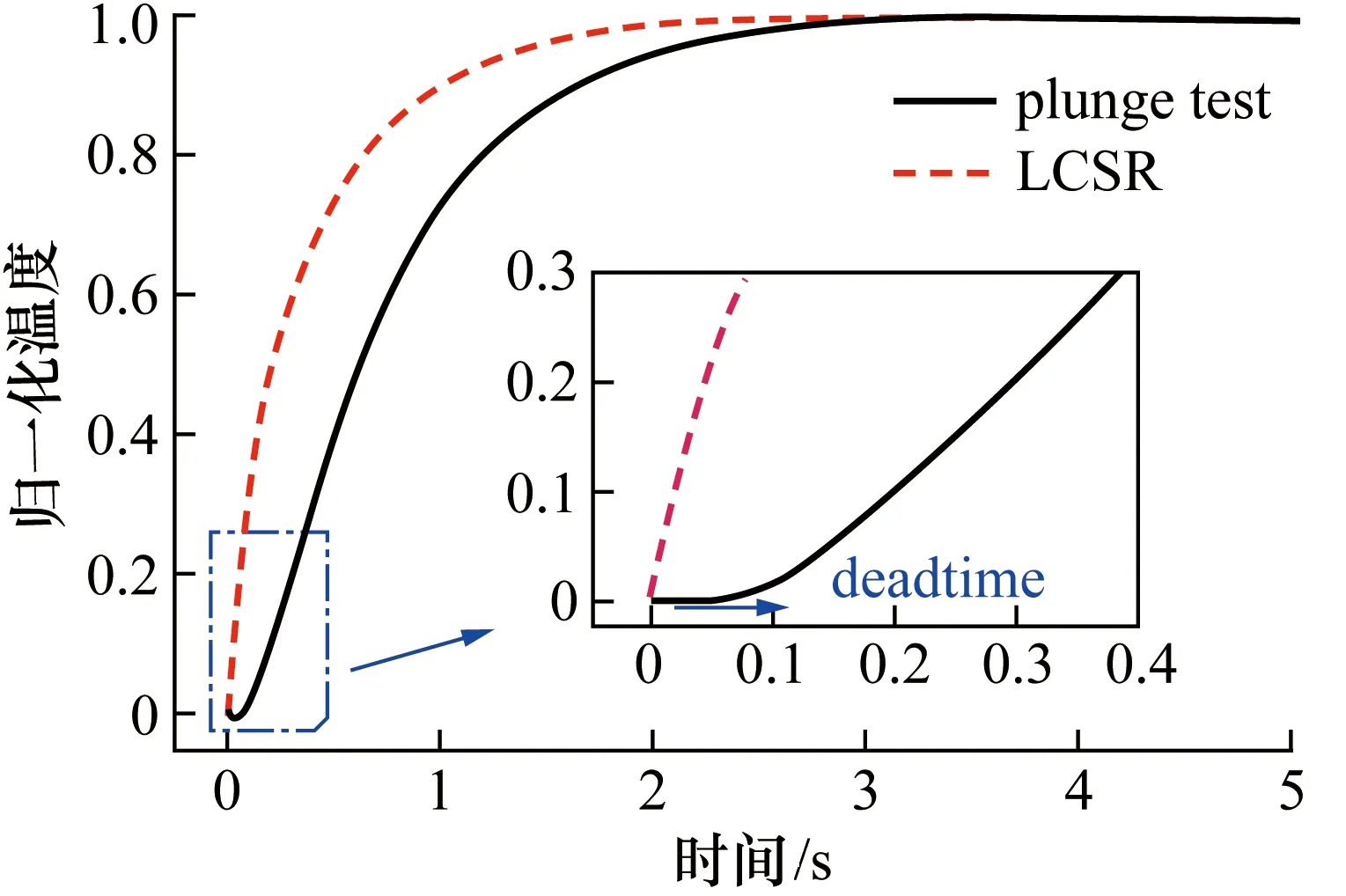
图6 插入法和LCSR法获得的热电偶动态响应曲线(r=0.996)Fig.6 The dynamic response of the thermocouple under plunge test and LCSR test (r=0.996)

将LCSR温度响应数据拟合到节点模型方程，然后对其作拉氏变换的反变换，可得出热电偶对应的模态响应方程:

R2(t)=B0+∑iBiexp(-Pit)

(3)

式中：t为时间；Pi为方程式的极点；B0、Bi为常数。

由于LCSR响应方程的极点与插入试验响应方程的极点一致，因而可计算出热电偶插入试验的响应方程:

R1(t)=A0+∑iAiexp(-Pit)

(4)

式中：A0、Ai为常数。

图7所示为r=0.996时，插入法和LCSR拟合、变换(i=2，3，4)获得的热电偶动态响应曲线。i=3时，LCSR拟合、变换得到的热电偶对周围流体温度阶跃变化的响应曲线与插入法得到的响应曲线最接近，局部放大图上显示时间常数也与插入法得到的时间常数最接近。这是由于当i=2时，拟合公式的项数较少，导致拟合、变换的误差较大；当i=4时，原始数据的噪声被放大，导致拟合、变换的误差增大，这与Rupnik等[16]的研究结论一致。

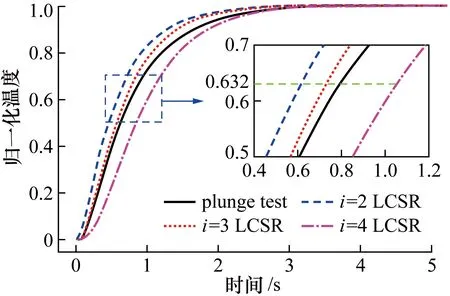
图7 插入法和LCSR拟合、变换获得的热电偶动态响应曲线(r=0.996)Fig.7 The dynamic response of the thermocouple by plungetest and fitted & transformed LCSR data (r=0.996)

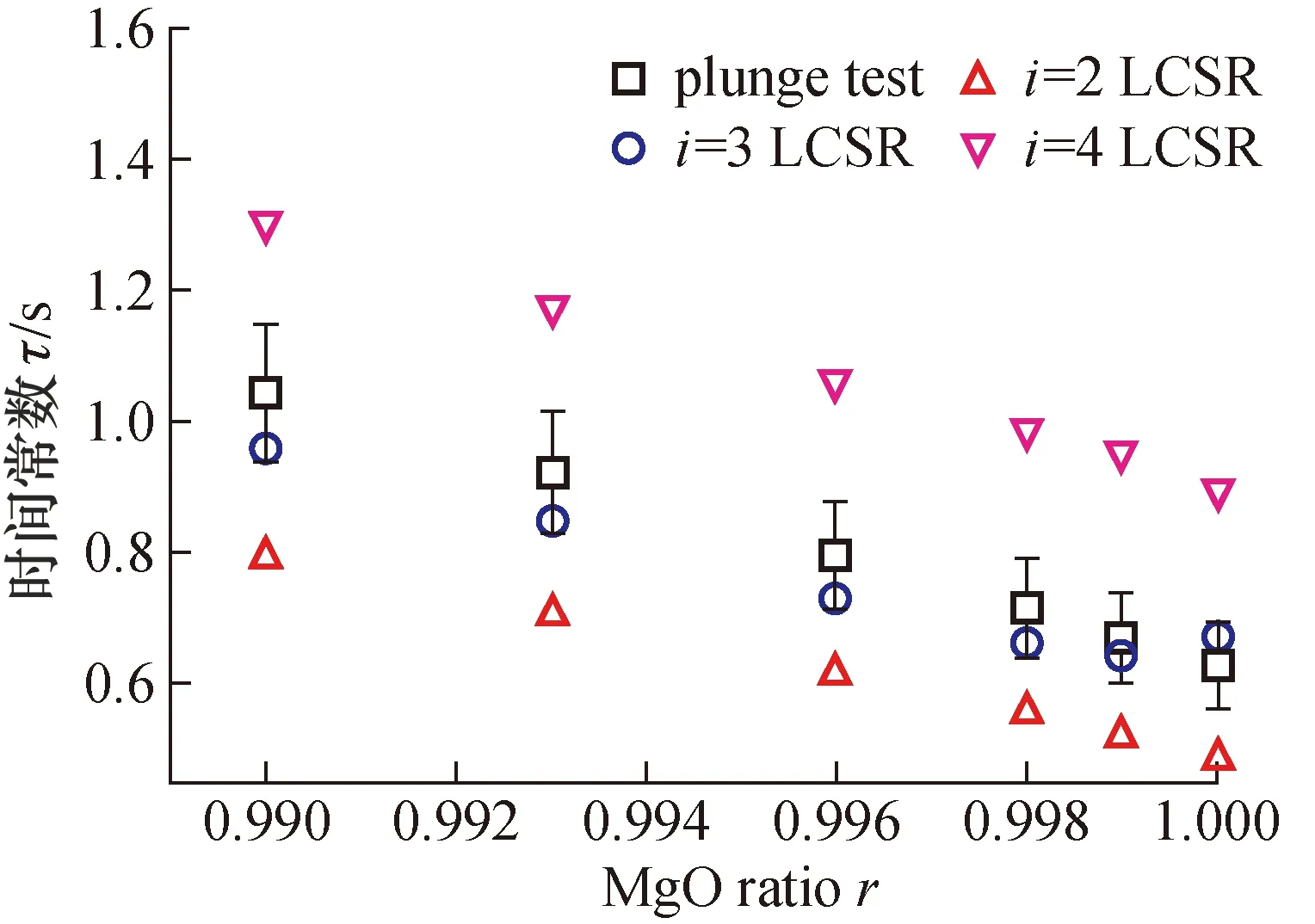
图8 插入法和LCSR拟合、变换获得的填充密实度对热电偶时间常数的影响Fig.8 Effect of MgO ratio on the time constant of the thermocouple by plunge test and LCSR

绝缘层MgO填充密实度r对热电偶时间常数τ的影响如图8所示。随着r增大，绝缘层的热导率增大，导致热电偶的响应速度加快、时间常数减小。不同r时，用式(3)和式(4)在i=2，3，4下拟合、变换LCSR响应方程，获得对应插入法的响应方程，求取时间常数。在i=3时求得的时间常数与插入法获得的时间常数最接近，且偏差小于10%。结果说明可以通过数值仿真的方法对热电偶的动态响应过程进行研究，结果偏差满足应用要求[16]。

6 结 论

采用有限体积法对铠装热电偶的动态响应过程进行了数值仿真，建立了热电偶保护管、绝缘层、感温层的三维模型，分析了网格划分尺寸对仿真结果的影响。在不同绝缘层MgO填充密实度下，研究了插入法和LCSR法获得的热电偶动态响应曲线，对LCSR响应数据进行拟合、变换，结果表明，随着填充密实度增大，绝缘层的热导率增大，热电偶的响应速度加快，时间常数减小。采用3个极点的响应方程对LCSR响应数据进行拟合、变换求得的时间常数与插入法获得的时间常数偏差小于10%，说明可以通过数值仿真的方法对铠装热电偶的动态响应过程进行研究，为快响应热电偶动态特性的设计、校准提供了一种新方法。