立式加工中心空间误差验证及补偿
2022-02-02王调品李峰
王调品,李峰
(1.成都工业职业技术学院装备制造学院,四川成都 610218;2.成都优拓优联万江科技有限公司,四川成都 611731)
0 前言
工业制造行业快速发展,如何提高数控机床加工精度一直是研究热点[1]。一般机床误差补偿[2]是提高加工精度的重要途径,通过人为提供一个新误差消去原来的误差,保证机床加工空间中任意实际点尽可能靠近理想位置。在误差补偿过程中,空间误差模型是研究基础,因此误差建模始终是广大学者研究的重要内容之一。基于多体系统理论及其齐次坐标转换的建模[3]技术因通用性较好被广泛采用。柏衡和沈建新[4]采用基于多体系统理论的建模方法,通过充分分析拓扑结构、机床几何误差与坐标系之间的转换矩阵,建立机床综合误差模型,为后期开展实时误差补偿提供了计算依据。陈康等人[5]根据多体系统理论建立了机床空间坐标系,描述了加工中心拓扑关系与相对运动方式,分析了机床结构中的几何误差,阐述了D-H描述运动体间坐标变换的矩阵,最终得到了机床空间综合误差模型,为机床仿真实验与误差补偿提供了数学模型依据。XIANG等[6]基于旋量理论计算了机床运动学通用模型,有效实现了机床空间误差预测与补偿实验。
综合以上分析,依据多体系统理论的数控机床空间误差建模及其补偿已经较为成熟,但是机床结构错综复杂,由于齐次坐标变换涉及多个局部坐标系,较为冗余、复杂,同时会出现丢失几何误差的情况并可能出现奇异性的问题。因此,本文作者基于旋量理论建立机床运动学正解,同时输出该立式加工中心完备空间误差模型,在分析21项几何误差的基础上进行某立式加工中心的空间误差建模,进一步借助运动学逆解补偿策略开展空间误差补偿实验,最终借助体对角线实验验证该方法的正确性和有效性。
1 立式加工中心空间误差建模
1.1 机床运动学正解模型
三轴立式加工中心结构简图如图1所示。机床旋量运动学[7]正解:将3根轴运动量(x,y,z)转换为机床刀具刀尖点相对于工件的位置偏差。机床运动链可以分为两部分:刀具运动链和工件运动链。刀具链为刀尖点到床身的运动链,而工件链是从工件切削点到床身的运动链。

图1 机床机构简图
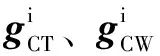
(1)
(2)
机床未进给时,gCT(0)、gCW(0)分别为机床刀具点和工件切削点在机床坐标系下的初始位置,分别如式(3)(4)所示:
gCT(0)=[xtytzt1]T
(3)
gCW(0)=[xwywzw1]T
(4)
综合以上分析,当前所建2条机床运动链正解本质上为理论运动轨迹,并未有几何误差参与,但实际上机床空间误差为刀尖点与切削点实际位姿之间的偏差。因此,应首先进行几何误差分析,然后进行机床运动链实际运动学正解推导,最后建立基于旋量理论运动学分析的机床空间误差模型。
1.2 几何误差定义
三坐标立式加工中心,一般只有x、y、z3个运动轴。当x轴单轴进给时,共计存在6项几何误差:δx(x)、δy(x)、δz(x)、εx(x)、εy(x)、εz(x),同理y轴、z轴同样分别存在6项几何误差,三轴共计18项几何误差。此外,x、y、z轴之间还有 3 项不直度误差εxy、εyz、εzx,因此三轴立式加工中心共有 21 项几何误差[8],如表1所示。因后续运动学建模过程中设定x轴为参考,因此x轴不存在不直度误差。图2所示为x轴几何误差示意。

表1 21项几何误差

图2 x轴几何误差示意
1.3 空间误差建模
机床空间误差建模的基础即是建立2条运动链实际运动学正解。依据旋量理论,结合第1.2节中21项几何误差分析结果,每一项几何误差均可看做微小旋量运动描述,因此以x轴为例,将各项几何误差以旋量指数积形式表示为
(5)
同理y轴、z轴分别表示为
(6)
(7)
机床运动链实际运动学:机床理想运动附加微小误差旋量运动。因此,通过结合21项几何误差分析,得出该立式加工中心刀具链、工件链实际运动学正解分别为
(8)
gCW(0)
(9)
结合机床运动链分析基础,建立该立式加工中心空间误差模型为

(10)
其中:ex、ey、ez分别为空间误差各轴向投影。
该立式加工中心空间误差模型包含了21项几何误差,实现了立式加工中心空间误差完备建模,不仅避免了主流建模方法奇异性问题,同时规避了可能出现的几何误差丢失问题。
2 几何误差测量与辨识
利用九线法[9]对21项几何误差辨识时,一般将几何误差称为辨识结果,而九线法实验测量数据实际上为误差综合结果,称作几何偏差。运用九线法辨识几何误差时,各轴各有3条测量路线。以x轴进给为例,当机床沿x轴轴向进行3条测量线进给时,线1选取测点A1(x1,y1,z1),测定x轴定位偏差Δδx1(x),继续测量x轴沿y向和z向的直线度偏差Δδy1(x)、Δδz1(x);线2选取测点B2(x2,y2,z2),测定x轴轴向定位偏差Δδx2(x),继续测量y向直线度偏差Δδy2(x);线3选取测点C3(x3,y3,z3),测得x轴向定位偏差为Δδx3(x)如图3所示。依据九线法测量原理可得式(11):

图3 九线法测试轨迹 图4 不直度偏差
(11)
进一步,如图4所示,根据相邻两方向上的直线度偏差数据即可计算剩余3项不直度误差εxy、εyz、εxz,如式(12)所示:
(12)
式中:D1、D2分别为x、y轴进给行程。同理,εyz、εxz亦可辨识。
同上所述,亦可辨识y轴、z轴各项几何误差。值得注意的是,机床进给轴一般不符合笛卡尔坐标系原则。因此,实验开始之前,应提前进行相关设置,保证机床进给轴与G代码实际运行轨迹相符,避免出现与预设进给方向相反的情况。
3 空间误差补偿及实验验证
3.1 机床运动学逆解
根据第1.1节中机床运动学正解定义,计算出三轴实际运动的过程如式(13)所示:
(13)
结合式(13)分析,基于式(1)(2)推导,展开机床运动学正解为
(14)
根据式(14)反推机床运动逆解为
[xyz0]T=gCW(0)·ΔgWT·gCT(0)-1
(15)
3.2 补偿方法
基于旋量理论的机床空间误差补偿路线[10]规划如图5所示。

图5 补偿策略流程

(3)计算预测轨迹与名义轨迹之间的偏差Δ;
(4)将偏差Δ作为补偿量附加到名义运动轨迹上;
(5)基于旋量运动学逆解,逆向求解误差补偿后的机床运动行程为(xc,yc,zc),即机床实际进给坐标。
3.3 实验验证
为验证基于旋量运动学分析的机床空间误差补偿方法的正确性,基于国际标准ISO230-6[11],采用第3.2节中的补偿路线,选用双频激光干涉仪为测量仪器,利用机床加工空间内4条体对角线定位偏差测量结果,通过比较体对角线补偿前后效果,验证补偿方法的准确性。体对角线测量轨迹及补偿结果如图6、图7及表2所示。
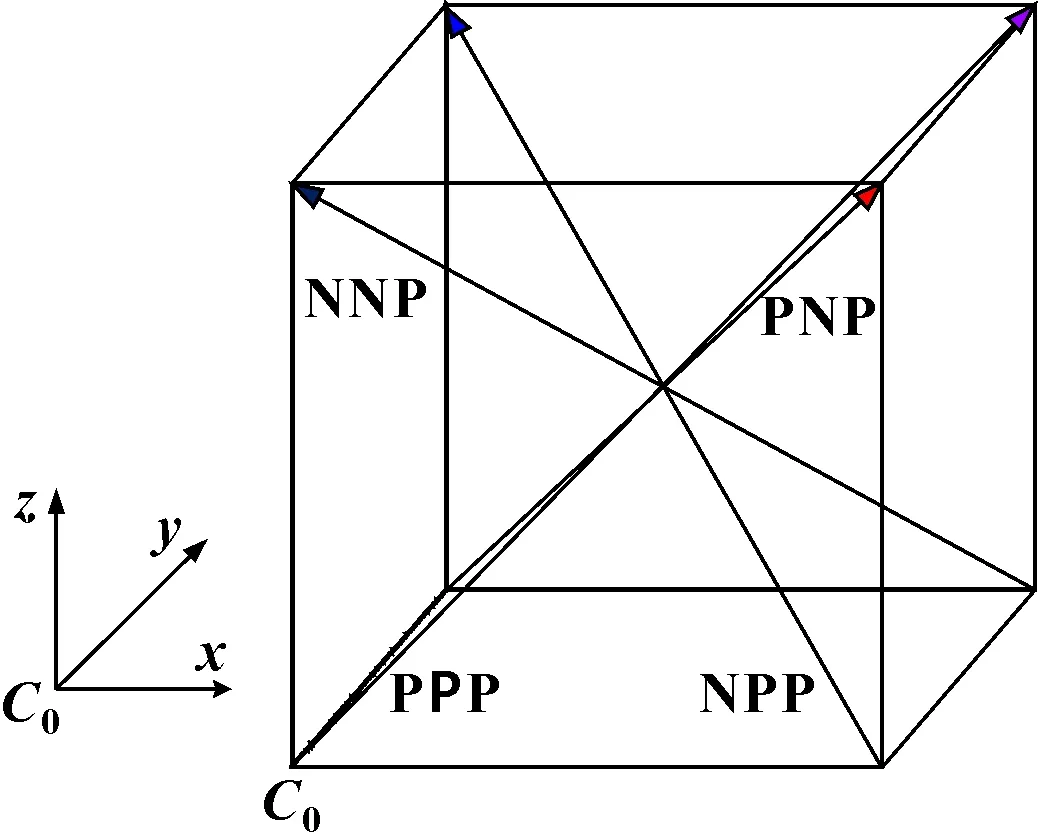
图6 体对角线测量轨迹
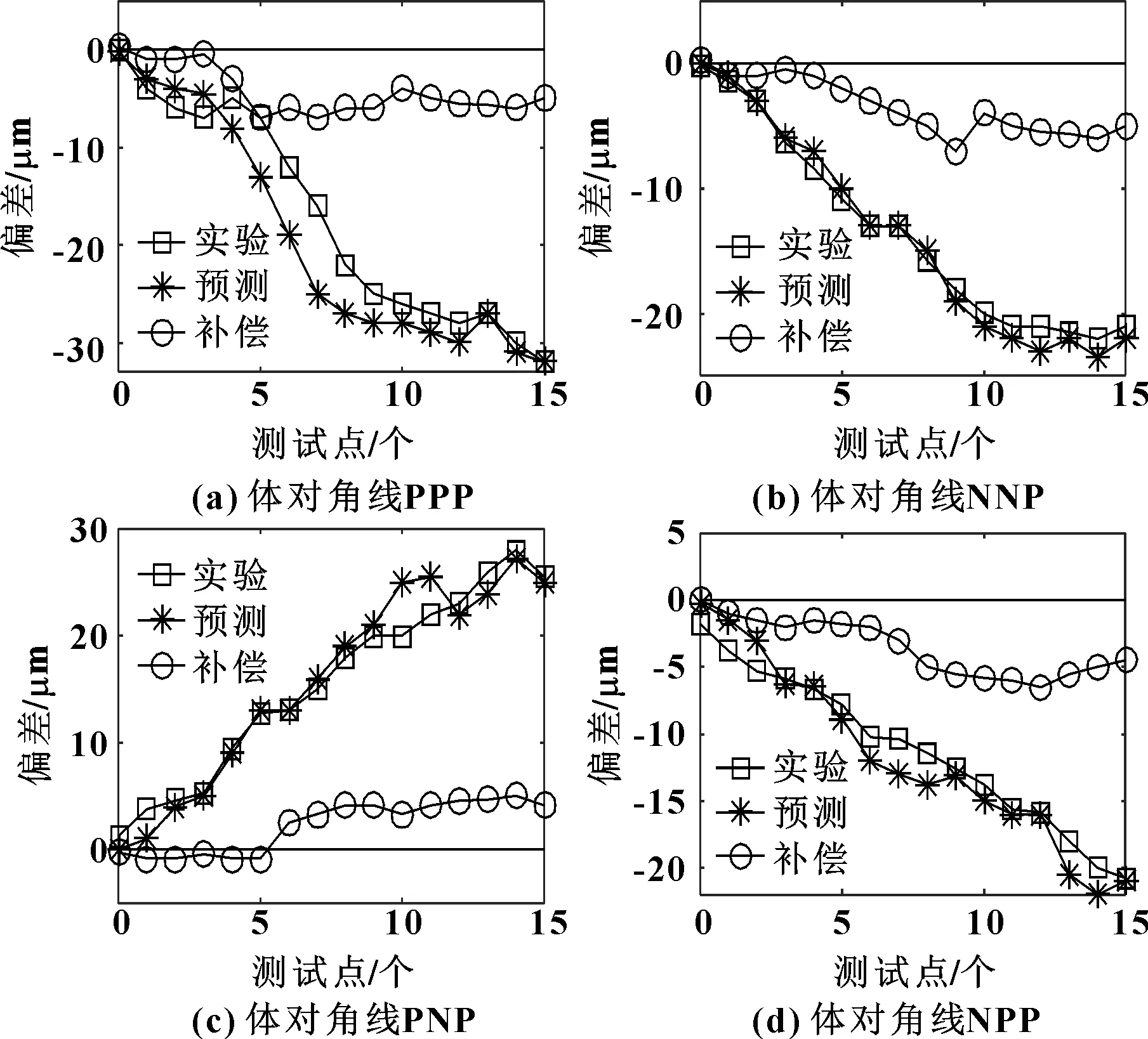
图7 体对角线补偿

表2 预测补偿结果
实验结果表明:4条体对角线实验与预测补偿结果符合预期,且体对角线正极限位置点最大补偿率达82.9%。补偿实验结果验证了基于旋量运动学分析的机床空间误差补偿方法的正确性,为提高机床整机加工精度提供了参考。
4 结论
(1)以提高某立式加工中心整机加工精度为研究目的,基于旋量理论推导机床运动链运动学正解,推导并构建了包含21项几何误差的立式加工中心完备空间误差模型。
(2)利用传统九线法辨识18项几何误差,同时借助直线度偏差计算3项不直度误差,为后续补偿提供数据基础。
(3)基于旋量理论的运动学逆解补偿策略和国际标准ISO230-6,通过对比4条体对角线补偿前后的结果,验证该补偿方法的可行性。结果表明:4条体对角线补偿结果均符合预期,最高补偿率达82.9%。实验结果不仅验证了补偿方法的可行性,同时为提高机床整机加工精度奠定了数据基础。
