应变对Mo2C(001)表面电子结构及光学性质的影响
2022-02-01吴星彤熊启杭岑伟富杨吟野
吴星彤,熊启杭,岑伟富,杨吟野
(1.贵州民族大学化学工程学院,贵阳 550025;2.贵州民族大学新能源与纳米材料重点实验室,贵阳 550025;3.贵州民族大学材料科学与工程学院,贵阳 550025)
0 引 言
随着社会的发展,资源、能源、环境与社会发展的矛盾日益凸显。研究人员提出有效利用太阳能解决人类发展面临的资源枯竭、能源危机和环境污染问题。因此太阳能利用效率、光吸收效率、电荷转移分离效率等的提高成为当今研究的热点问题。半导体因具备光的吸收、载流子的产生、光电输运的可控性等优点备受研究者关注,有望应用于太阳能领域,推动实际应用,带动社会经济效益[1-3]。
碳化钼是一种典型的渗碳体,主要有α-MoC1-x、β-Mo2C、η-MoC、γ-MoC四种晶相[4-6]。由于碳原子进入钼原子间的间隙,形成独特的电子结构,Mo原子表现出优异的活性,为其在半导体光电子领域的应用奠定基础。其中β-Mo2C作为一种新的二维类石墨烯结构材料MXenes,形成Mo-C-Mo顺序堆叠结构,Mo原子处于最外层,C原子处于Mo原子层之间的八面体间隙中,展现出独特的电子和光学性质,在储能、吸附、光电传感器、催化[7-8]、超导性[9-11]、钠离子电池[12]等领域展现出巨大的潜力,吸引了科研工作者的关注和研究[13-19]。
2009年,Liu等[20]利用基于密度泛函理论的第一性原理平面波赝势法,对Ortho-Mo2C和Hexa-Mo2C的生成焓和电子结构进行研究,发现Ortho-Mo2C比Hexa-Mo2C更容易生成,并且在两种结构的Mo2C电子体系中形成共价键,能带结构呈现金属特性。2012年,Vrubel等[21]首次报道β-Mo2C是具备良好活性的电催化剂。2017年,Mortazavi等[22]使用第一性原理密度泛函理论计算模拟了单层和独立式Mo2C的力学和光学响应,研究结果发现在不同加载方向上弹性特性相近的情况下,应力-应变曲线的非线性状态有很大的不同。模拟还表明,Mo2C薄膜在单轴加载时仍保留其金属电子特性,Mo2C纳米膜的介电函数沿平面内和平面外方向呈各向异性。2022年,Khalil等使用密度泛函理论(density functional theory, DFT)的第一性原理计算Mo2C的电子结构、弹性常数、声子色散、光学性质和各种热物理性质。研究结果表明:Mo2C是各向异性的硬质金属材料,可加工性和延展性良好,热导率低[23]。Du等利用广义梯度近似(generalized gradient approximation, GGA)中的Perdew-Burke-Emzerhof (PBE)方法计算得到Mo2C晶格参数为0.3 nm。Wu等利用广义梯度中PBE+U方法研究了一系列单壁纳米结构的Mo2C,发现卷为纳米管结构后Mo2C表现出磁性金属特性[24]。综述理论和实验发现,在β-Mo2C晶体中Mo原子和C原子之间以强的共价键和金属键结合,Mo原子之间以较弱的共价键结合,这使得Mo2C容易沿着(001)面滑移,从而造成微尺度的塑性变形。在变形过程中,平行于受力方向的基面容易通过位错滑移使晶粒变形。但是Mo2C的滑移系少,位错的滑移只局限于基面,这为剥离Mo2C提供理论支撑。
最近,本课题组在理论上研究发现,由于β-Mo2C层与层之间的结合力是范德瓦耳斯力[25],易剥离,且剥离后处于表面的Mo原子具有更高的活性。结合电子轨道分析可知,表面Mo原子的d轨道容易被C原子的核外电子填充,形成d轨道与碳原子轨道上的杂化能级,导致Mo原子的d轨道宽度变小,呈现出金属特性,有效地调控β-Mo2C的性能。鉴于此,为了拓宽β-Mo2C在半导体光电子领域的应用,课题组尝试通过调节β-Mo2C晶体的变形实现对表面Mo原子活性的调节,采用能带工程理论技术调制β-Mo2C的带隙实现对β-Mo2C体系光电子跃迁的调制,提高光的吸收率、载流子迁移率、光电输运量等。本文采用第一性原理方法,研究不同应变下Mo2C(001)表面的电子结构和光学性质,为改善和优化Mo2C的光电子性能,提高光能利用率提供理论基础。
1 计算模型与理论基础
1.1 计算模型
Mo2C属于六方晶系结构,其空间群为P63/mmc,晶格常数a=b=0.3 nm,c=0.54 nm。从Mo2C的晶体结构分析发现,原子在(001)面呈现层状分布,并且原子层处于c轴方向的1/4、1/2、3/4处。因此在建立表面模型时,为了保证原子结构的完整性,选择[001]方向建立表面结构模型,表面原子层厚度是晶格常数c的整数倍,得到完整的表面,结构模型如图1所示。

图1 Mo2C(001)表面结构模型Fig.1 Structure model of Mo2C(001) surface
采用基于第一性原理的赝势平面波方法计算Mo2C的能带结构、电子态密度和光学性质。所有的计算由CASTEP (Cambridge serial total energy package)软件包完成[26-28]。采用BFGS (Broy-den, Fletcher, Goldfarb and Shannon)方法对Mo2C几何结构进行优化[29]。为了获得能量最低的计算方法,论文采用GGA-PBE近似方法对Mo2C的几何结构进行优化,几何结构优化时施加(110)面的应变,在应变的基础上继续进行几何结构优化,得到弛豫的结构,下文所有的计算均在此结构基础上进行。采用超软赝势(ultra soft pseudo-potential, USPP)处理离子实与电子之间的相互作用[26]。原子间作用力的收敛阈值为0.02 eV/nm,内应力不大于0.1 GPa,原子位移的收敛阈值为0.02 pm,两次迭代之间的能量收敛标准为1.0×10-5eV/atom,自洽场收敛标准为5.0×10-6eV/atom,平面波截断能为360 eV,Monkors-Pack布里渊区的k点选取为4×4×2,参与计算的价态电子选取Mo 4d55s1。
1.2 应变理论
应变是用来度量物体变形程度的量,假设Mo2C(001)面是连续、均匀、正交各向异性的材料,并且应变在线弹性与小变形的范围内,则Mo2C(001)面的应变为线性的正应变:
(1)
(2)
式中:x0是[100]方向的原长;y0是[010]方向的原长;x是[100]方向变形后的长度;y是[010]方向变形后的长度。当x>x0时,εx>0;x
2 结果与讨论
2.1 能带结构与态密度
能带结构是分析光电子半导体材料的重要依据,计算得到应变作用下Mo2C沿布里渊区高对称点方向的能带结构,如图2所示。图2(a)~(i)为Mo2C在应变作用下的能带结构图,费米能级在Ef=0 eV处,图2(e)为平衡状态(未施加应变)下的能带结构,Mo2C呈现带隙值为0.696 eV的间接带隙半导体,当应变为5%、10%、15%和20%时,Mo2C还是呈现为间接带隙半导体,带隙值分别为0.708 eV、0.604 eV、0.437 eV和0.309 eV,可以看出随着应变的逐渐增大,Mo2C的带隙值先增大后减小。当应变在0%~5%时,价带顶在布里渊区A点,导带底在布里渊区K~G之间,当应变为5%时带隙最大;当应变在10%~15%时,价带顶在布里渊区M~L之间,导带底在布里渊区A~H之间并且导带底随着应变增加向费米能级方向移动,导致带隙减少。
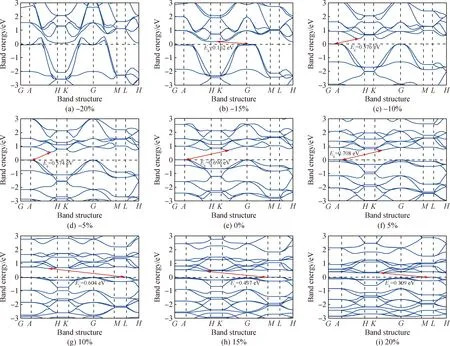
图2 不同应变下的能带结构图Fig.2 Band structure under different strains
当应变为-15%、-10%、-5%时,Mo2C的能带结构呈现出间接带隙,带隙值分别为0.574 eV、0.376 eV和0.162 eV,带隙值的变化主要是由导带底向费米能级移动所致;当应变为-20%时,Mo2C的能带结构没有带隙,呈现出金属特性。其原因是当Mo2C受到应变时,原子间隙和电子轨道耦合程度发生变化,部分电子轨道的能级也发生变化,使得价带电子迁移到导带所需能量也跟着变化,即晶体中原子的相对位置发生变化迫使原子发生重组,因此晶格常数相应发生变化使得其能带结构发生变化。结果表明,无论施加拉应变还是压应变均能改变Mo2C的能带结构,其主要改变的是费米能级附近的势场,导致价带底和导带顶的有效质量发生变化。通过调节应变可以观察到带隙值在-20%~20%的应变范围内呈现准线性变化的规律。
图3为态密度图。态密度分布是判断导电性能的一个重要因素,为了研究应变调制对体系亚电子结构的影响,计算了Mo2C体系中各原子对应电子的分态密度随应变的变化情况。图3(a)~(f)分别为Mo2C(001)表面在-20%~20%应变下的分波态密度图,费米能级Ef选择在0 eV。由图3可知,应变对Mo2C态密度的影响主要体现在Mo 4p、4d和C 3p态电子的变化上。在价带区域,随着应变从-20%变化到20%,Mo 5s、Mo 4p、Mo 4d和C 3s、C 3p电子在费米能级(E=0 eV)处的贡献逐渐减小,尤其是Mo 4d和C 3p电子在费米能级附近受影响最显著;在导带区域,随着应变从-20%变化到20%,Mo 5s、4p电子在费米能级(E=0 eV)附近的贡献逐渐减小。根据布局分析可知其变化的原因主要是应变导致Mo2C(00)表面的势场发生变化,Mo原子和C原子上的电荷分布受应变的影响重新分布,费米能级附近的电荷态密度发生变化。

图3 不同应变下的态密度图Fig.3 Density of states under different strains
2.2 光学性质
2.2.1 介电函数
图4是Mo2C(001)表面在不同应变作用下的介电函数图。介电函数是沟通带间跃迁微观物理过程与固体电子结构的桥梁,通过介电函数可以得到其他各种光谱信息。图4(a)是应变作用下Mo2C(001)表面的介电函数实部图,介电函数实部数值代表位移电流对磁场的贡献率,介电函数实部数值越大,束缚电荷的能力越强。光子能量为0(无入射光)时对应的是静态介电常数。从图4(a)可知,平衡状态下Mo2C(001)表面的静态介电常数为16.64。当应变为-10%、-5%时,静态介电常数对压应变不是很敏感,继续增大压应变时,静态介电常数才有了显著的变化。当应变为5%、10%、15%和20%时,静态介电常数分别为6.267、17.443、33.964、57.424。由此可知静态介电常数随着应变的增大逐渐增大。随着光电子能量的增加,介电函数逐渐减小,在光电子能量为2.5 eV附近取得最小值。与未施加应变的Mo2C(001)表面相比,拉应变能显著影响Mo2C(001)表面的光学性质。随着光电子能量增加,介电函数在4~6 eV的能量范围波动随着应变的变化逐渐削弱,说明应变从-20%变化到20%的过程中,Mo2C的极化能力削弱,电子云与原子核的电荷中心的距离发生相对位移进而减小。在光电子能量为0~4 eV时,应变为-20%的介电函数明显偏离其他介电函数,为了明晰其原因,需结合介电函数虚部作进一步解释。
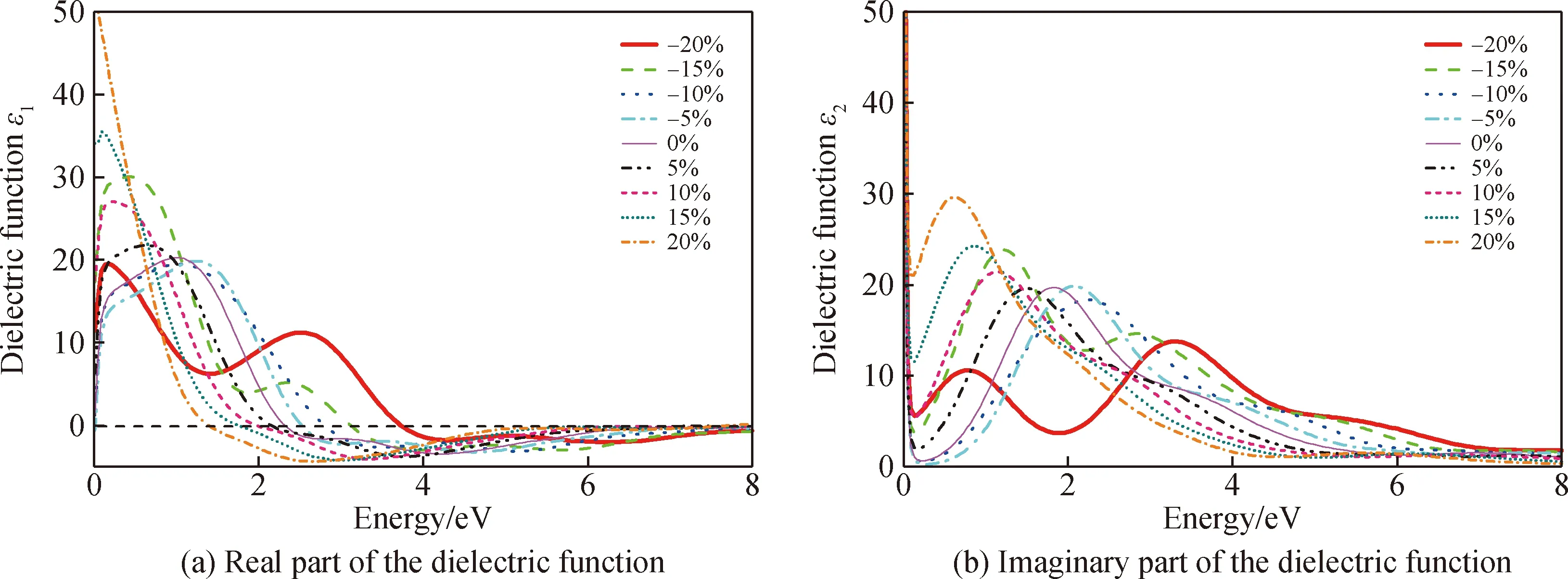
图4 不同应变下的介电函数图Fig.4 Dielectric function under different strains
介电函数虚部表征的是形成电偶极子消耗的能量,是传导电流对磁场的贡献率,取决于导带和价带的电子跃迁能。虚部数值越大,表明电子吸收光子的概率越大,处于激发态的电子数目越多,进行下一步跃迁的概率也越大。图4(b)是介电函数虚部图,由图可知,介电函数第一峰随着应变的增加逐渐增加,表明拉应变的施加有利于电子的跃迁。随着光电子能量的增加,介电函数虚部先增大后减小,最后趋于一个稳定值。当光电子能量约为0.6 eV时,出现了一个最强吸收峰,表明在低能区Mo2C(001)表面有较强的光吸收能力。当应变增加到-20%时,出现了两个吸收峰且峰值明显低于其他峰,这是因为当应变增加到-20%时,Mo2C原子之间的原子距离及键合方式发生变化,导致Mo2C对光的吸收降低。结合电子态密度(见图3)分析可知介电函数的变化规律与Mo 4d、C 3p电子态密度的变化相似,即介电函数虚部电子的跃迁主要来源于Mo 4d和C 3p态电子。
2.2.2 反射率和吸收率
图5是Mo2C(001)表面在不同应变作用下的反射率图和吸收率图。图5(a)是Mo2C的反射率图,由图可知,当施加拉应变时,随着应变的增加,Mo2C的反射特性逐渐增加。在0~10 eV的能量范围内,Mo2C的反射谱存在3个明显的反射峰,在4 eV处达到最大值。随着光电子能量的逐渐增加,反射特性逐渐减小。当施加压应变时,在0~5 eV的能量范围内,随着光电子能量的增加,反射特性先增大再减小,在2 eV附近达到最小值,之后随着光电子能量的增加再次增加,在4 eV附近达到最大值,反射特性走势与介电函数虚部走势一致。由吸收系数和介电函数的关系:
(3)
可以得到Mo2C的吸收系数如图5(b)所示。式中α为介质的吸收系数,ε2为介电函数虚部,n为折射率,ω为角频率,C为真空中的光速。吸收峰主要来源于激发态电子在价带顶和导带底之间的跃迁。从图5(b)可知, Mo2C的光吸收带边随着应变从-20%变化到20%,其吸收带边向高能方向偏移,第一吸收峰峰值随着压应变的增加逐渐增加,随着拉应变的增大而逐渐减小。但当光电子能量大于5 eV,在-20%~0%的应变作用下吸收峰比0%~20%应变的高,这表明在此条件下受激发的电子比0%~20%应变下的多。因此-20%~0%的应变有助于光生载流子在晶体内的扩散、跃迁,对Mo2C(001)表面Mo 4d和C 3p 电子-空穴对的激发、跃迁有利。

图5 不同应变下Mo2C (001)表面的反射率和吸收率Fig.5 Reflectivity and absorptivity of Mo2C (001) surface under different strains
2.2.3 折射率和消光系数
折射率是吸收性介质最主要的光学参数,由复折射率与介电函数的关系得到。图6为Mo2C(001)表面在不同应变作用下的折射率图和消光系数图。折射率本质上反映了材料的电磁结构在光波作用下的极化性质或光电特性。图6(a)为Mo2C(001)表面在不同应变作用下的折射率图,平衡状态下Mo2C(001)表面的静态折射率为4.04。当施加应变后折射率发生显著的变化,随着应变从-20%变化到20%,折射率逐渐减小,第一峰的峰值也减小,第一峰对应的能量增加,但应变大于10%,折射率增加不显著。随着光电子能量的增加,折射率逐渐减小。当光电子能量大于2.5 eV时,-20%应变的折射率明显高于其他应变下的折射率,变化趋势与介电函数实部走势一致,表明折射率的变化主要取决于Mo 4d电子跃迁。

图6 不同应变下Mo2C(001)表面的折射率和消光系数Fig.6 Refractive index and extinction coefficient of Mo2C(001) surface under different strains
消光系数描述了介质对光的吸收。图6(b)为Mo2C(001)表面在不同应变作用下的消光系数图。当应变为0%,消光系数第一峰对应的能量值出现在2 eV处;当施加应变时,消光系数第一峰对应的能量值向低能方向移动。在4~6 eV能量范围内,随着光电子能量的增加,消光系数呈递减趋势,光学性质减弱,表明在这个能量范围内,Mo2C(001)表面对光的吸收较少。
3 结 论
本文采用第一性原理方法研究Mo2C(001)表面的电子结构与光学性质,通过调节应变研究其表面的电子结构和光学性质,得到如下结论:
(1)当应变为0%、5%、10%、15%和20%时,Mo2C(001)表面的能带带隙值分别为0.696 eV、0.708 eV、0.604 eV、0.437 eV和0.309 eV,可以看出Mo2C(001)表面的能带随着应变的增加带隙先增大后减小,当应变为-15%、-10%、-5%时,Mo2C(001)表面的能带带隙值分别为0.574 eV、0.376 eV和0.162 eV。但是在整个变化过程中Mo2C(001)仍然是间接带隙半导体,当应变为5%时带隙达到最大值,表明应变能够有效地调节Mo2C(001)表面的能带结构和电子特性。
(2)在应变的作用下,Mo2C(001)的介电常数和介电函数第一峰峰值随着应变增加而增大,介电函数虚部随着应变的增加均向低能方向移动;吸收率计算结果表明,在0~20 eV的能量,随着压应变的增加吸收增强,随着拉应变的增加吸收减弱,消光系数表现出相似的变化规律。表明压应变有益于光的吸收,拉应变抑制光的吸收,即通过应变可有效调节光学的利用率。
