近岸沙坝海滩裂流数值模拟与动力学分析

衣骊安，张希彬

（1.西北大学，陕西 西安 710127；2.天津科技大学，天津 300457）

裂流又称离岸流，是在海浪辐射应力及压力差的作用下，经波浪破碎后高于岸边的水体通过破浪带，回流入海的条带状表面流，具有持续时间短、流速快、尺度小、流向几乎与海岸线垂直的特点。裂流灾害严重影响海滨休闲活动，是滨海旅游区的“隐形杀手”。全球范围内有80%～90%的海滩救援事件与裂流有关，每年有数千人死于裂流[1-2]。许多发达国家都已经把裂流预报作为日常预报之一。如美国国家天气服务中心把全美所有海滩的裂流预报作为冲浪区预报的一部分，澳大利亚政府在重要海滩发布裂流预报信息，以保障游客的人身安全。我国滨海存在裂流多发区，特别是在青岛、厦门等旅游海域。但是我国目前对裂流灾害的相关调查评估、精细化预警报和公众科普警示等都很少[3]，需要进行精细化的裂流数值模拟研究，有效预防和降低裂流灾害风险。

1936年，SHEPARD F P[4]首次提出裂流的概念，认为裂流是一股强而窄的离岸水流，从破碎区一直延伸到破碎带以外，指出裂流的强度和延伸的距离与入射波的波高有关，是近岸环流的一部分。BOWEN A J等[5]提出，产生裂流的常见地形是被裂流槽间断的沿岸沙坝，流场和海滩的侧面边界的相互作用也能产生裂流[6-8]。随后，各国学者对裂流表面流场、流速结构和悬沙通量等特征进行了观测实验[9-12]。2018年7月，我国国家海洋局海洋减灾中心首次对广东粤西重点海滨旅游区进行了裂流风险联合调研[3]。裂流理论研究需要以高精度的现场观测、实验和模拟数据为基础。由于裂流的不稳定性和瞬变性等特点，现场观测实验的时空覆盖率具有局限性，利用数值模拟方法研究和预测裂流，是裂流研究的未来发展趋势。

目前适用于数值模拟裂流的波浪模型主要分为两类，波浪平均模型和波浪分辨模型[13-14]。波浪平均模型只能计算亚稳态平均裂流流速，无法精确计算由于短波峰产生的瞬时裂流。波浪分辨模型可以充分考虑波浪和流的耦合效应，从而能够更加精确地得到裂流变化的时间过程。FUNWAVE（Fully Nonlinear Boussinesq Wave Model）模型是由美国特拉华大学海岸工程研究中心开发的完全非线性的Boussinesq模型，是目前模拟裂流最为代表性模型之一，模型采用WEI G等[15]提出的完全非线性弱频散方程，包含了波浪引起的动量通量和近似涡流校正，并引入造波、摩擦阻尼、边界吸收和波破碎等附加项来模拟这些效应。在随机波与波相互作用条件下能够模拟裂流的演变，FUNWAVE模型能够计算从中等深水区到冲浪带的波浪传播、折射和破碎过程，计算瞬时流场和水面的变化，目前广泛用于近岸波生流场的数值模拟，可以用来模拟近岸波浪和环流等[16]。

SHIN C H等[17]利用FUNWAVE波浪分辨模型，模拟了韩国海云台海滩的裂流灾害，并利用遥感影像对模拟结果进行了验证，研究了蜂巢型波浪条件下裂流发生的动力机制。CHOI J等[18]利用FUNWAVE模型模拟了韩国大川海滩的裂流，并分析了在耗散型海滩由巨尖海滩产生的裂流形态特征。WANG H等[19]利用FUNWAVE模型对弧线形近岸海滩裂流的特征进行了研究。裂流的产生涉及近岸波浪的破碎和强烈的近岸海滩沉积物的输运，由于裂流强度较大，泥沙等沉积物被向海方向输运，容易形成裂流沟槽。本文针对常见沙坝沟槽型海滩的裂流过程进行数值模拟研究，研究沙坝沟槽海滩的裂流影响因素，并对FUNWAVE波浪分辨模型和传统波浪平均模型进行比较，说明使用FUNWAVE波浪分辨模型，能够更精确地模拟裂流，便于对裂流灾害进行风险评估。

1 模型设置与验证

基于FUNWAVE模型，对裂流进行数值模拟。首先利用HALLER M C等[20]的沙坝海岸裂流物理模型实验数据，对FUNWAVE模型模拟裂流的有效性进行了验证。HALLER M C等开展的裂流物理实验具有开创性，其研究了规则波在双沟槽沙坝海岸地形上产生的裂流。实验对裂流沟槽附近的流场进行了测量，研究了裂流与平均水面变化的关系，指出裂流的构成形态，该组实验数据也被广泛应用于各种近岸波生流数学模型的验证。Haller裂流物理实验设置的地形三维数据中，裂流沟槽宽度是1.8 m，两端沙坝各长3.65 m，关于沟槽中心线对称，沙坝顶端水深是0.048 m，造波板处水深是0.363 m。实验过程中水池地形不是严格对称的，在沿岸方向也不是很均匀。但是由于地形的沿岸非均匀性对测量结果影响较小，因此，很多学者都利用Haller物理实验的数据来验证裂流[21]。

利用FUNWAVE进行裂流数值模拟，图1是本文根据Haller物理实验的地形数据，设置的地形及水深图。由于地形的对称性，本文采用Haller物理实验中地形宽度为实际宽度的一半进行数值模拟计算[21]。初始条件使用规则入射波，波周期为1.0 s，波高为0.048 m，造波源位于x=2 m处。其中数值实验中计算区域的网格分辨率是△x=0.05 m，△y=0.1 m，时间步长和空间步长的选取满足Courant稳定条件，模拟时间为200 s，选取20～200 s的数值模拟数据进行统计分析。将模拟数据与实验数据进行对比验证，主要比较波浪增减水的分布特征、各断面的均方根波高、波浪破碎点位置和波浪破碎后波高的衰减现象，研究裂流平均流速U和V分量，验证模型模拟结果的有效性。

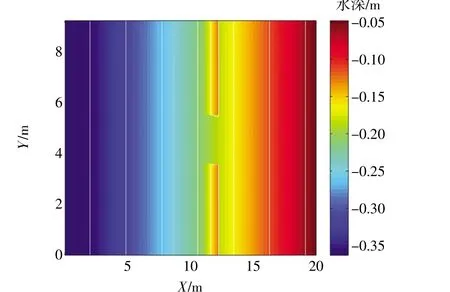
图1 Haller实验数值模拟采用的地形和水深数据

根据Haller物理实验中的测量数据，我们进行了模拟数据的对比分析，详见图2至图5。图2显示数值模拟的均方根波高的分布，由于沙坝的存在使波浪提前破碎，波高急剧衰减，裂流沟槽水深较大，波浪破碎较晚，波高较大。沙坝存在处增水变化较大，中间沟槽处增减水较小。波高的不均匀分布，意味着辐射应力的分布不均匀，存在明显的梯度，进而导致波浪增水存在差别。模型较好地模拟了波浪破碎点位置和波浪破碎后波高的衰减现象。图3显示截面处平均海平面水位的变化。破波带外由于波浪爬高导致平均水面下降，破波带内辐射应力减小，动量平衡使得平均水面上升。沙坝存在处的增水变化明显。图4和图5模拟了离岸方向流速分量和沿岸方向流速分量的分布特征。从图4显示出，在x=12.3 m处的裂流沟槽内，出现明显的负向水流，即离岸裂流。从图5显示出，在x=10 m处的向海侧，流速几乎衰减为零。与Haller实验数据相比，模拟数据的波高和水位的变化，都较好刻画了波浪的波动性质，变化趋势与测量数据基本吻合，模拟的流场主要是流速的变化过程从数值到变化趋势都与实验数据相一致。此外，模拟的数据与实验数据存在误差，这可能是由于模拟时采用沿岸均匀地形所致[22]。总之，利用FUNWAVE模型，能够较好地模拟裂流特征。

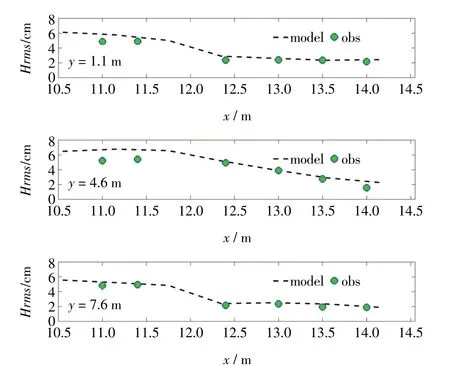
图2 均方根波高实测与模拟比较

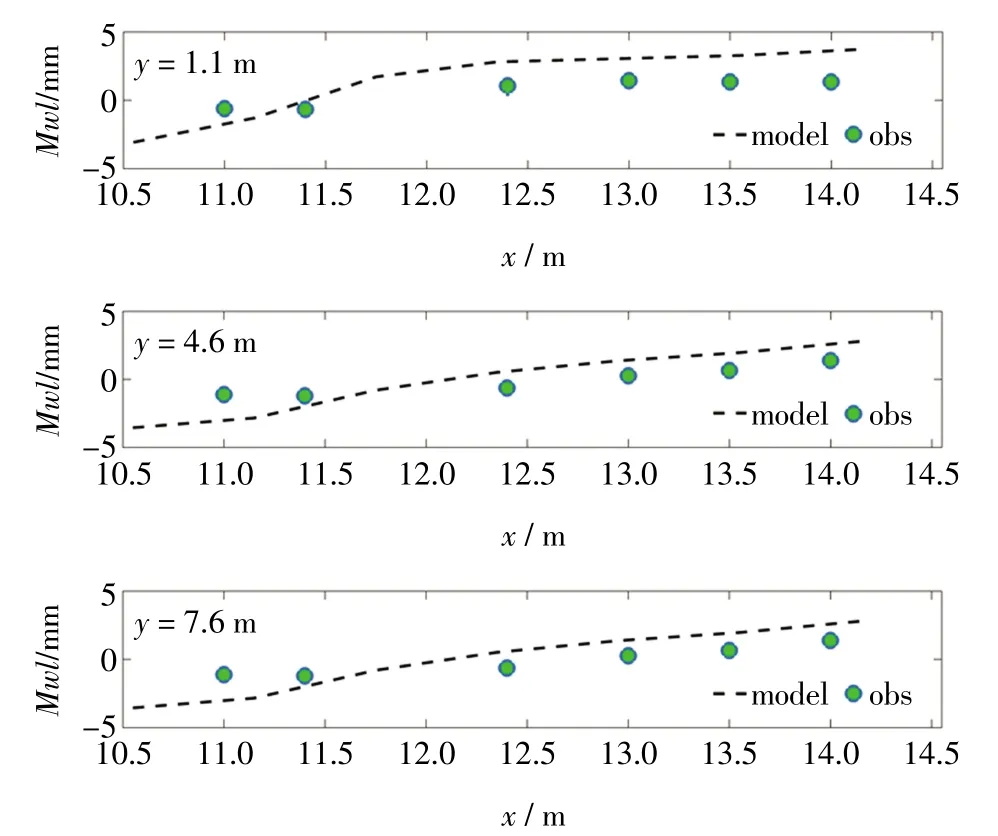
图3 平均海平面实测与模拟比较

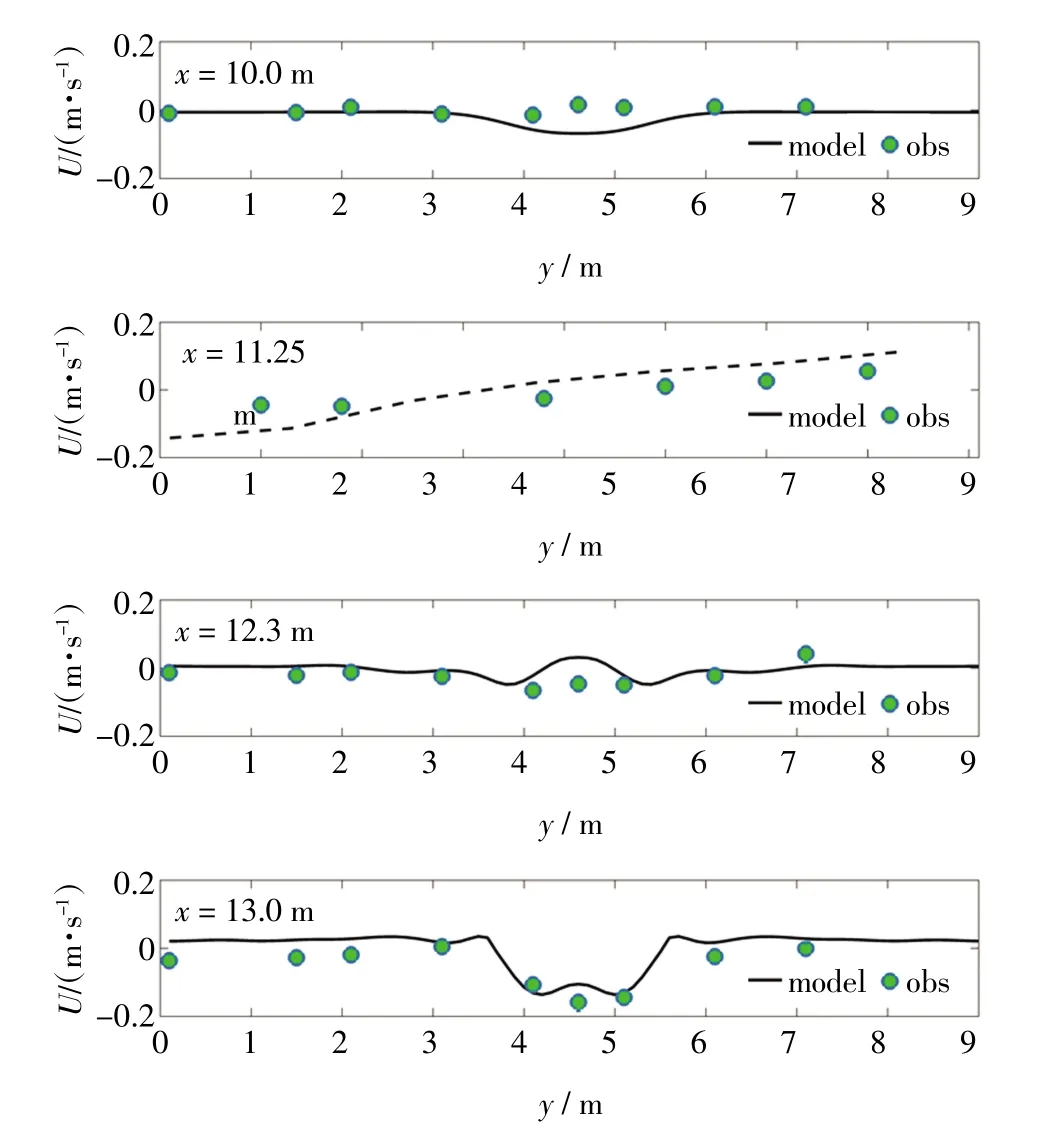
图4 离岸方向流速实测与模拟比较

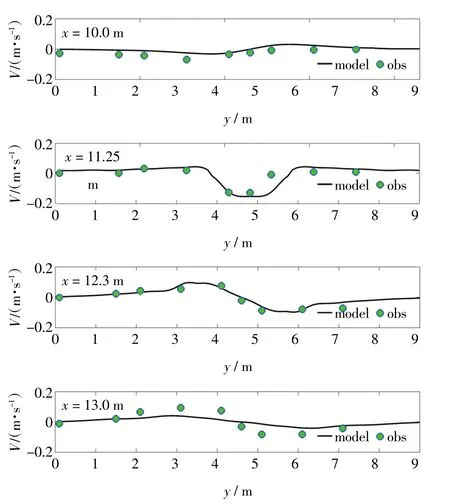
图5 沿岸方向流速实测与模拟比较

2 裂流数值模拟及结果分析

为了研究裂流的动力学特征及其影响因素，本文设置如图6所示的常见沙坝沟槽海滩地形，并利用FUNWAVE模型进行裂流数值模拟。模型的计算区域设置为500 m2×1 000 m2，其中的网格分辨率是：△x=1 m，△y=2 m。设置规则入射波条件，波向垂直于岸线方向，波高H=0.6 m，波周期T=6 s，模型的模拟时间是1 200 s，选取100～1 200 s模拟数据进行统计分析。

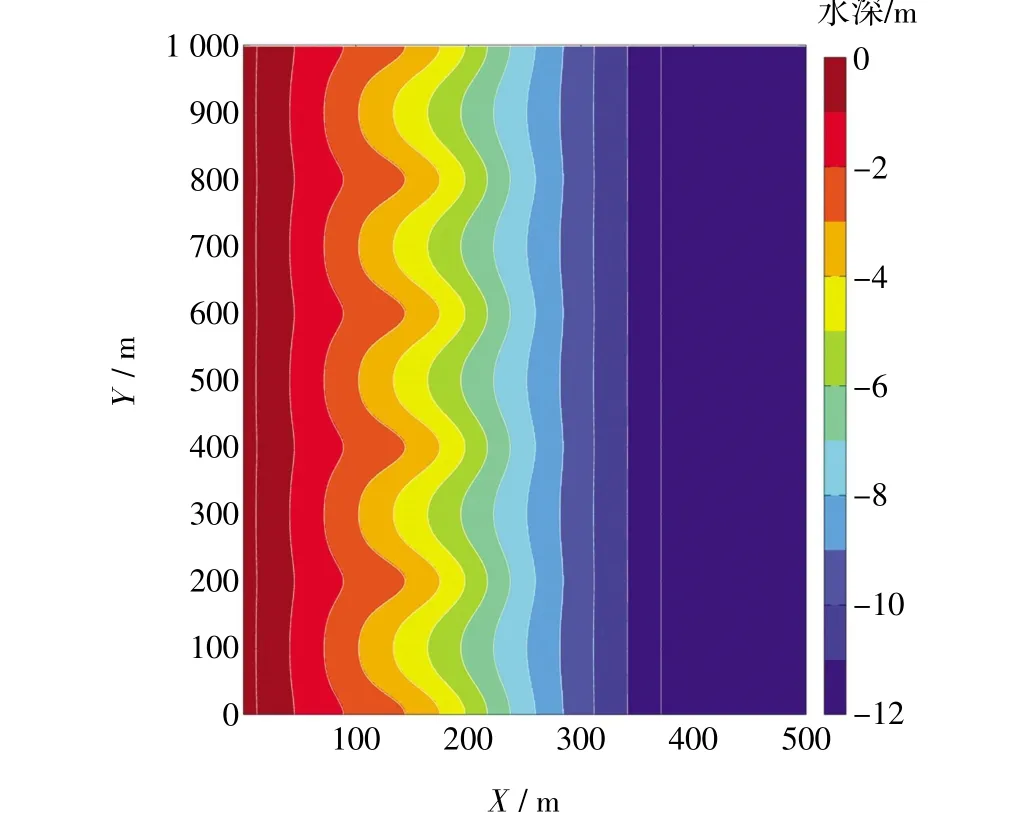
图6 模拟的沙坝海滩地形和水深

2.1 裂流动力学分析

裂流产生于波浪折射引起的辐射应力梯度的增加，裂流一般由波能较高处，流向向海方向的波能较低的裂流沟槽处，因此裂流会从波高较高的近岸海域流向向海方向波高较低的裂流沟槽海域。通过模拟计算不同时刻的瞬时海平面水位、均方根波高、涡流场和流场的运动形态（图7），对裂流过程的动力学特征进行了分析。

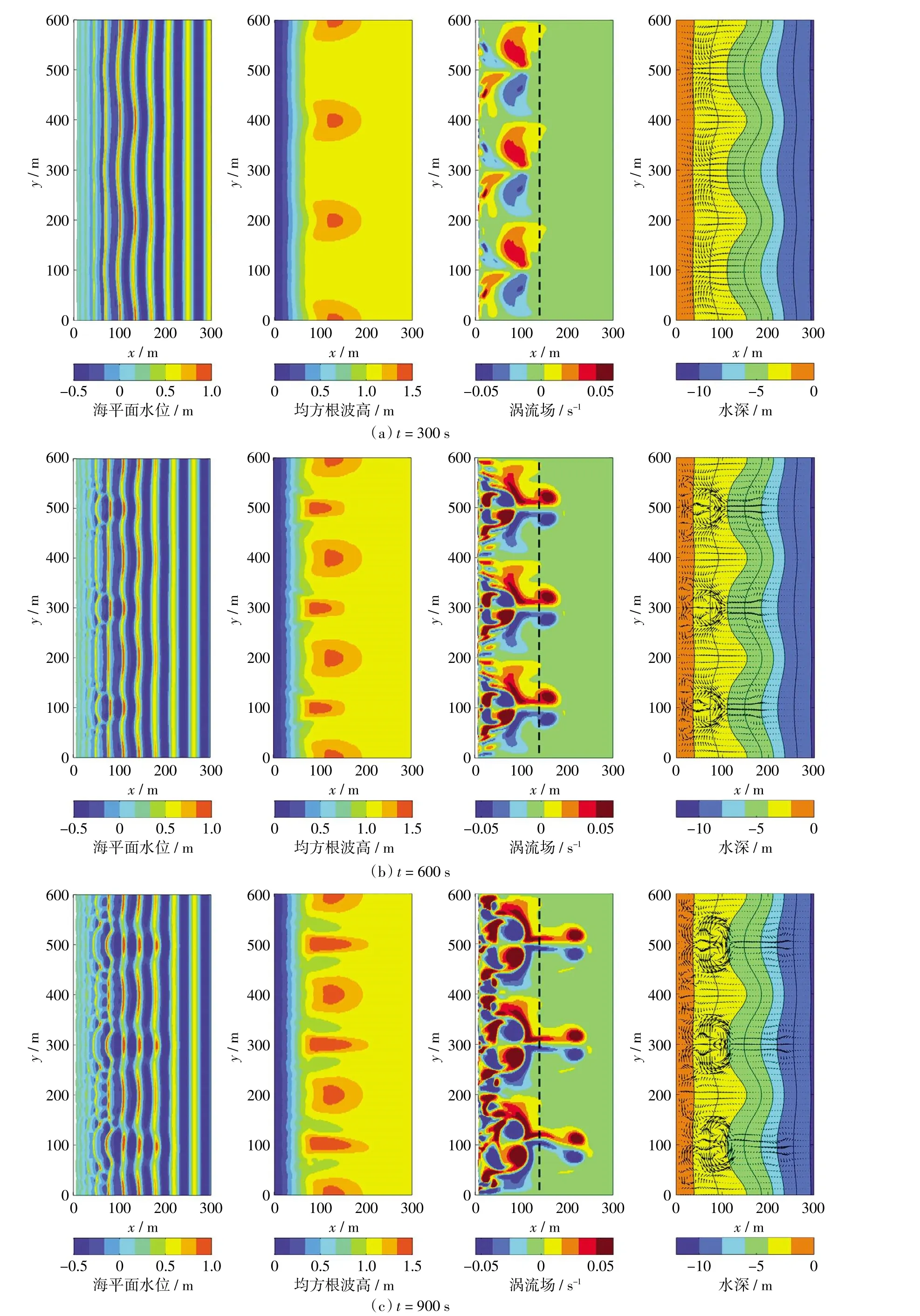
图7 裂流期间瞬时海平面水位、均方根波高、涡流场和流场分布

在裂流初期，平均海平面水位幅值较弱，全场波峰线基本平行。随着时间的增加，裂流逐渐增大，由于向岸传播的波浪的相互作用，波峰线发生向海侧弯曲，并促使波浪在离岸方向产生汇聚现象。随着涡流场和流场继续发展，波面沿着沙坝沟槽向海侧移动，波面最大值出现在沟槽内向海侧。

随着裂流的发展，沙坝上波浪发生破碎，波高变小，沟槽内水深较大，波浪破碎位置更靠近岸线。沟槽两侧沙坝顶端出现涡对。当波浪从深水区越过沙坝，到达浅水区，波高增加，两个沙坝部分是高能量区，波高较高，接着波浪破碎并迅速衰减，沿岸波高最低。沙坝中间的沟槽，波高较高，是高能量集中区，并且有两个基本对称的弱的低能量区在两边，波高也较低。

当t=300 s时，波浪由波高较高的沙坝浅滩高能量区域，流向向海方向波高较低的低能量沟槽海域。并且在沙坝浅滩，出现了较弱的成对涡流场。当t=600 s时，在向海侧，三组强的离岸流在高能量区汇集。流速达到了0.35 m/s，与裂流特征一致，同时在沙坝浅滩和沟槽区域，每个裂流伴随对称的涡旋，上述流动共同构成了裂流系统。t=900 s时，裂流和涡对继续向深水区运动，并且幅值衰减，由于波浪和裂流的共同作用，沟槽内出现波高拥堵现象，出现全场波高的极值，裂流出现不稳定性。

2.2 裂流影响因素分析

设计敏感裂流实验，研究了入射波高、波角和潮汐水位对裂流强度的影响。图8（a）显示，当入射波周期T=10 s时，随着入射波高从0.4 m到1.0 m逐渐增大，裂流最大平均流速在增加，裂流危险程度增大。裂流强度与潮汐水位有关，取低潮位100 cm、中等潮位200 cm和高潮位300 cm，对裂流过程进行数值模拟。图8（b）显示，低潮位时对裂流的影响较大，使裂流最大平均流速增加，对应的裂流强度增大。图8（c）显示，在入射波垂直岸线入射时，裂流离岸方向的U分量流速最大，裂流流速分量随着入射波角的增加而减少，随着时间的增加，裂流最大离岸方向U分量平均流速达到了一个渐近的程度。图8（d）显示，不同的入射波角的变化，都使波浪平均最大流速较大，这也说明入射波角度的不规则性，能够产生较大强度的沿岸流。分析原因，主要是波浪入射角度的增加，增加了沿岸方向V流速分量，因此总流速是增加的趋势，相对来讲，对应的离岸裂流流速相对是减弱的。

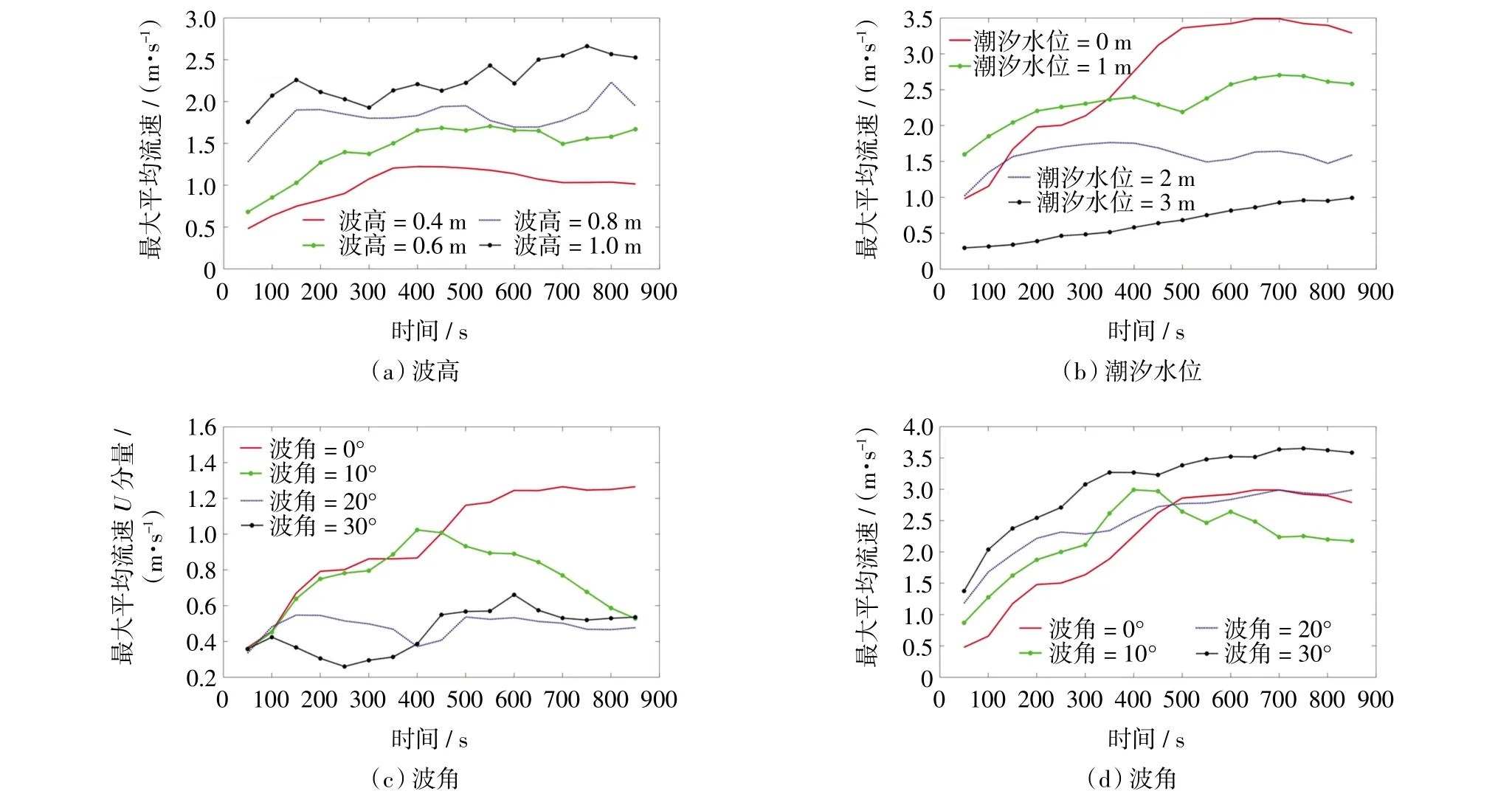
图8 波高、潮汐水位和波角对裂流最大平均流速的影响

2.3 不同时间平均裂流时均流速的比较

利用数值模拟结果，研究不同时间间隔的裂流平均流速，对裂流灾害风险的影响。

图9显示在研究区域x=100 m截面，t=800 s时刻流速的变化特征。计算得到该时刻平均流速的变化，波平均的时间间隔分别是50 s、100 s和200 s。图9（a）显示裂流流速离岸方向U分量的变化，可以发现进行流速平均的时间间隔越大，时均流速越小，特别是在流速高峰值和流速低峰值的时刻，比如在高峰值y=32 m处，进行50 s平均的时均流速是0.9 m/s，进行200 s平均的时均流速是0.6 m/s，流速分量减小了33%。而在低峰值y=44 m处，时均流速分量减少了57%，并且流速的方向也发生了改变。图9（b）显示的是沿岸方向V流速分量的变化，沿岸流时均流速在较大时间间隔下的平均流速显示减少的趋势，特别是在流速变化较大的最高和最低峰值附近，相比在零流速附近，由于流速变化不大，因此时均流速的变化不明显。图9（c）显示裂流总流速的变化，时间间隔较大，计算的平均流速值改变较大，相对有减少的趋势，因此能够低估裂流流速。由此可以看出，利用传统的波浪平均模型，计算的时均流速会减少裂流流速分量，并使流向发生改变，低估裂流流速，使裂流风险预测不够准确。而利用波浪分辨模型，才能精确计算出瞬时裂流流速和流速阈值。图10显示时间间隔分别为50 s、100 s和200 s，计算得到的裂流最大时均流速的分布。可以看出，不同波平均的裂流时均流速大小改变较大。时间平均的间隔为50 s时，计算的最大平均流速是1.4 m/s，时间间隔为100 s时，计算的最大平均流速是1.36 m/s，流速值减少了2.9%，而时间间隔为200 s时，计算的最大平均流速是1.27 m/s，流速值减少了9.2%。因此，在进行了裂流数值模拟时，时均流速的时间间隔较小，计算的平均流速越精确，能够较好地反映出裂流流速的阈值和裂流灾害的危险程度。

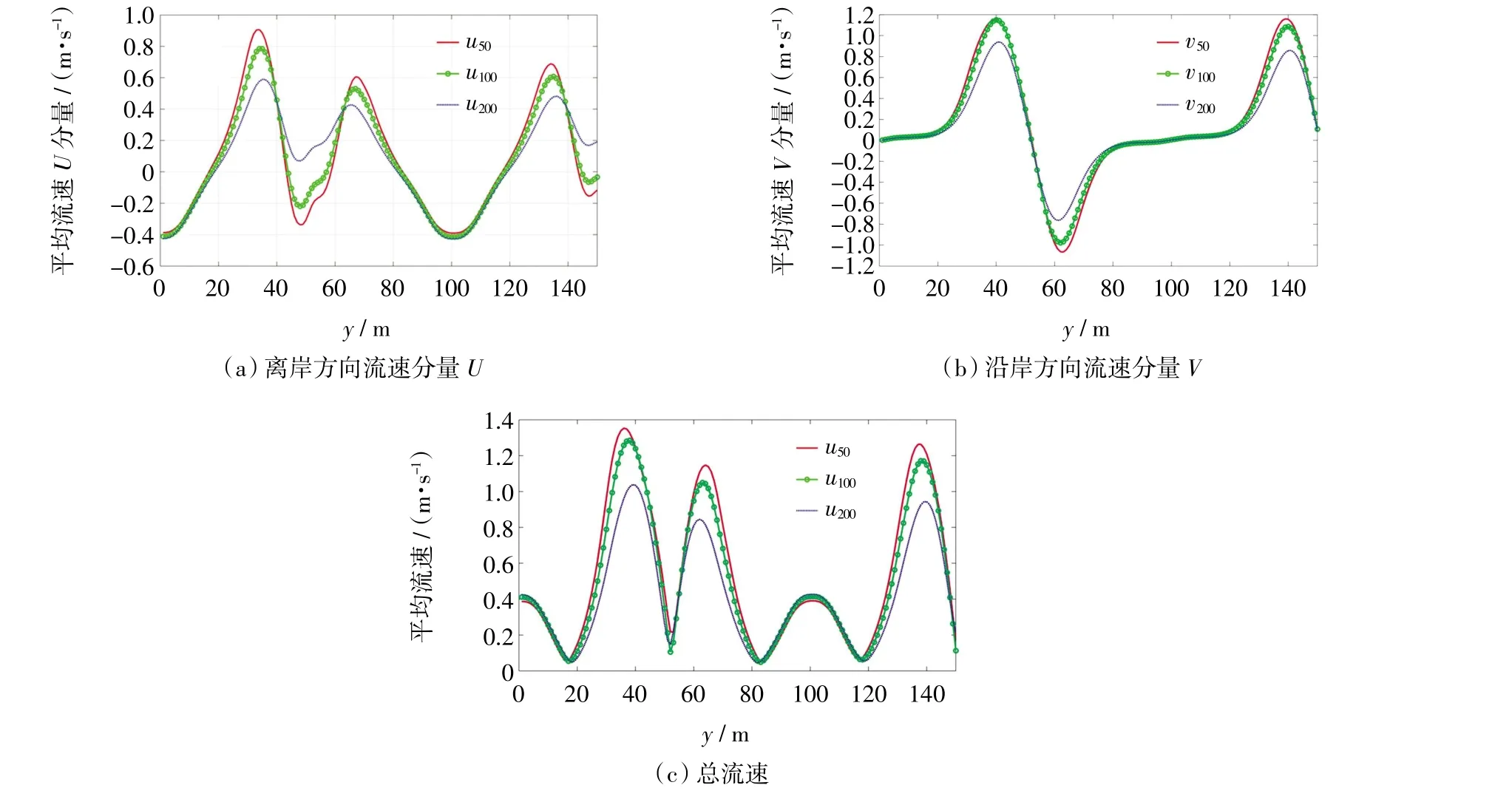
图9 不同时间平均的流速的比较

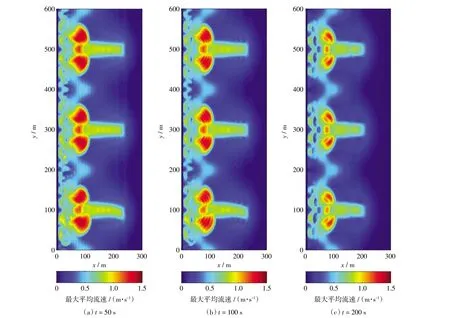
图10 不同时间平均的裂流最大平均流速的分布

3 结 论

本文利用FUNWAVE波浪分辨模型，对典型沙坝沟槽海滩的裂流灾害进行了数值模拟。利用Haller裂流物理实验数据对模型进行验证，说明模型对裂流数值模拟的有效性。利用数值模拟结果，研究了裂流发生过程中，平均海平面水位、均方根波高、涡流场和裂流流场的分布特征。通过设计裂流敏感实验，研究了沙坝沟槽海滩的裂流影响因素，指出裂流强度随着入射波高的增大而逐渐增加，入射角度的增加，会降低裂流的强度。研究了潮汐水位大小对裂流灾害的影响，低潮位时，裂流强度明显增大。最后，计算了不同时间平均的裂流时均流速的改变，研究表明，利用传统的波浪平均模型只能计算亚稳态平均裂流流速，模拟的裂流平均流速较小，容易低估裂流灾害风险，只有利用波浪分辨模型才能给出瞬时裂流流速和流速阈值，对裂流灾害进行合理评估。