基于等效因子的Q 学习燃料电池汽车能量管理策略

尹燕莉，张鑫新，潘小亮，詹 森，黄学江，王福振

（1.重庆交通大学 机电与车辆工程学院，重庆400074，中国；2.重庆长安汽车股份有限公司，重庆401120,中国；3.包头北奔重型汽车有限公司，包头014000,中国）

燃料电池混合动力汽车由于能够实现零排放，并且效率高，瞬时响应快，被认为是新能源汽车的理想车型。研究燃料电池混合动力汽车的能量管理问题，对于燃料电池汽车的发展具有重要意义。

近年来，能量管理系统作为混合动力汽车的核心，已在油-电混合动力汽车上得到了广泛的研究和应用，呈现出由基于规则[1-3]向基于全局优化[4-7]和基于瞬时优化[8]的发展趋势。研究中学者们也将能量管理应用到燃料电池汽车上，比如WANG Yujie[9]等提出了基于规则的控制策略，虽然该策略减少了燃料电池的功率波动，但基于规则的控制策略通常依靠经验值获得，优化效果有待进一步提高。SUN Haochen[8]等针对3 个动力源的燃料电池汽车，提出了改进的等效燃料消耗最小算法，提高了算法的计算效率，但是基于瞬时优化的控制策略不能保证在整个运行工况内的最优。XU Liangfei[10]等通过改进动态规则（dynamic programming,DP）算法，虽然能够在已知工况下获得真正意义上的全局最优解，但是计算量大，计算时间长，使得全局优化的实用性降低，通常只作为评价其他策略的标准。与此同时，也有学者通过智能算法对燃料电池汽车的能量管理问题进行研究，WU Xiaohua[11]等采用凸优化方法对插电式燃料电池汽车(plug-in fuel-cell electric vehicles,PFCEV)的动力源进行优化 ;林歆悠[12]等提出了行驶里程自适应的的控制策略，通过自适应的等效系数来维持PFCEV 的动力电池荷电状态(state of charge,SOC)平衡；但上述研究大多数都是针对插电式燃料电池汽车，对于以燃料电池为主要动力源、蓄电池为辅助动力源的功率混合型燃料电池汽车研究较少。

等效因子作为影响整车燃油经济性和维持蓄电池SOC 平衡的重要因素，决定着不同能量源的使用倾向,不少学者对等效因子的确定和优化开展了深入研究。S.Barsali[13]等将发动机的油耗和蓄电池耗费电能的等效油耗统一起来，作为解决实时优化问题的目标函数，提出了恒等效因子的控制策略，并指出等效因子是研究等效燃油消耗最小控制策略的关键；ZHENG Qing[14]等考虑到实时优化控制的局限性，通过动态规划算法在不同工况下对等效因子进行优化求解，与基于规则的控制策略进行对比，表明所提出的等效因子具有良好的控制效果。上述基于等效因子的能量管理策略大多是针对油电式混合动力汽车，而对于燃料电池汽车以经济性为目标的控制策略，早期的研究多是只考虑燃料电池的耗氢量，没有引入等效耗氢量的概念，对经济性的评价并不全面。随着研究的不断深入，目前大多数针对燃料电池汽车的能量管理策略都将等效耗氢量考虑在目标函数中，但并没有对燃料电池消耗的氢量与蓄电池电量消耗和补偿的能量等效转化平衡机理进行深入研究。

因此，本文将以燃料电池为主要动力源、蓄电池为辅助动力源的燃料电池混合动力汽车作为研究对象，基于FCHEV 动力源能量流动平衡机理，构建蓄电池电能转换为等效耗氢量的等效因子模型，提出基于能量流动平衡机理等效因子的Q 学习算法的能量管理策略，将离线优化和实时应用相结合，离线获得最优动力源输出功率，再根据实际工况信息对燃料电池和蓄电池的输出功率进行实时分配，获得较好的优化效果，减少等效氢消耗量，提高燃料经济性，同时维持SOC 平衡。

1 燃料电池汽车的建模

1.1 结构与动力总成模型

燃料电池汽车的动力系统结构如图1 所示，整车主要参数如表1 所示。

表1 整车主要参数

图1 燃料电池汽车动力系统结构

FCHEV 的能量管理问题，动力系统的功率平衡关系表示为

其中：Pm为电动机需求功率；Pfc为燃料电池输出功率；ηDC为DC/DC 转换器效率；Pbat为蓄电池输出功率。

整车驱动时，驾驶循环只考虑车辆的空气阻力、加速阻力、滚动阻力，未考虑坡度的影响，因此需求功率Preq、车轮处的转矩Tw可表示为：

其中：A为迎风面积；v为车速；m为整车质量；g为重力加速度；CD、f、δ分别为空气阻力因数、滚动阻力因数、旋转质量换算系数；Fa为加速阻力；Fw为空气阻力；Ff为滚动阻力；r为车轮半径。

1.2 电动机模型

电动机转矩Tm和转速nm为：

其中：ηi为传动系机械效率；i为主减速比；nw为车轮处的转速。

电动机功率为

其中：ηm电动机效率，ηm是关于nm和Tm的函数，用实验数据获得的电动机效率MAP 图如图2 所示。

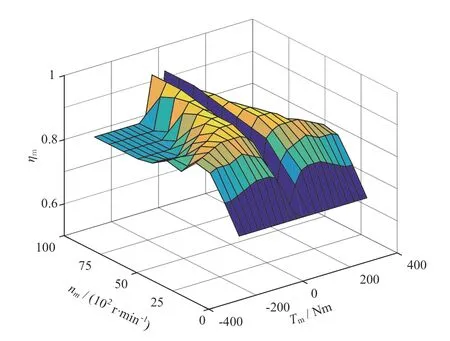
图2 电动机效率MAP 图

1.3 燃料电池模型

研究中选用的燃料电池是Advisor 汽车仿真软件中的FC_ANL50H2 准静态氢消耗模型[15-16]，耗氢率和效率-输出功率的关系曲线如图3 所示。

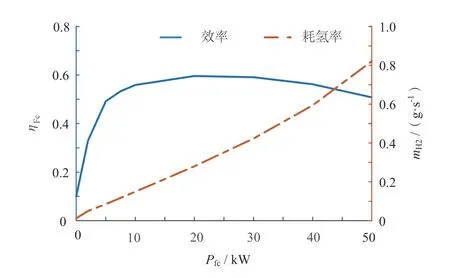
图3 燃料电池效率和耗氢率曲线

由图3 可见，燃料电池的输出功率在10～40 kW 时，燃料电池处在高效率区内，可获得更高的工作效率，进而可减少氢的消耗。研究中认为燃料电池运行稳定，燃料电池的氢耗量mfc由燃料电池的功率和对应的效率确定，表示为

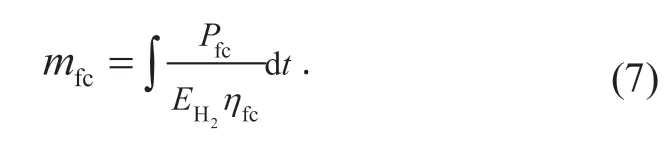
其中：Pfc为燃料电池的输出功率；EH2为氢气低热值，EH2=120 kJ/g；ηfc为燃料电池的效率。

1.4 蓄电池模型

采用12Ah 的锂电池，通过开路电压与内阻串联的方式，建立Rint 的等效电路，如图4 所示。忽略温度对电池组的影响，蓄电池的充放电内阻，开路电压只与SOC 有关。

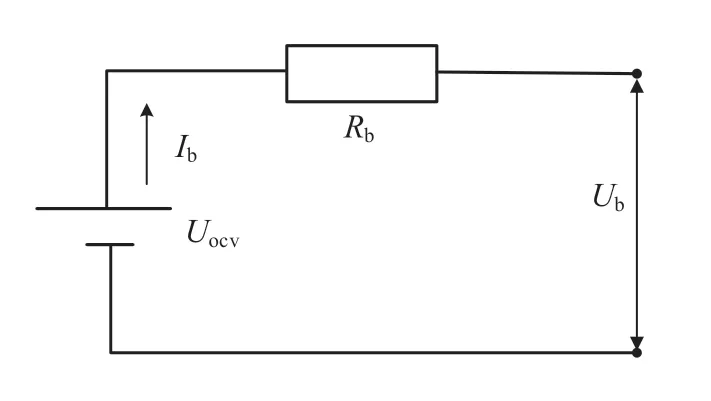
图4 Rint 等效电路

总线电压Ub根据Rint 等效电路计算得到，Ub可表示为

其中：Ub为总线电压；Uocv为蓄电池组开路电压；Ib为蓄电池电流；Rb为蓄电池内阻。

在蓄电池输出功率Pbat、内阻Rb、开路电压Uocv已知的情况下，蓄电池组电流Ib按式（9）计算。

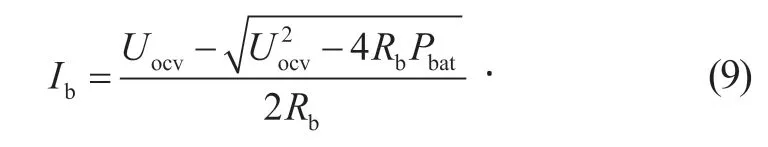
蓄电池的荷电状态SOC 可表示为

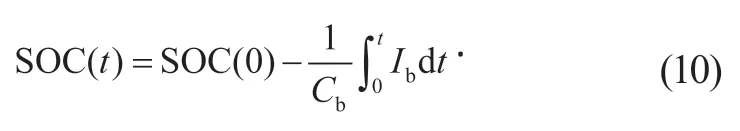
其中，Cb为蓄电池的容量。

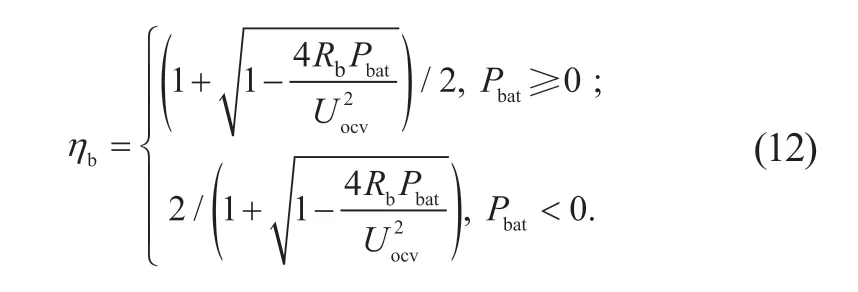
蓄电池的瞬时充放电效率ηb可表示为：

将式(9)带入式(11)得到：

2 基于Q 学习的燃料电池汽车能量管理策略

由于车辆实际行驶过程中行驶工况的随机性，需求功率难以准确预测。Q 学习算法不依赖于已知模型，在处理复杂的系统优化问题时有明显的优势。因此，本文基于Q 学习算法，对FCHEV 动力系统动力源的输出功率进行优化分配，以寻求整个行驶过程中能量消耗最小化。

2.1 状态、动作及回报值的设定

以车速v、需求功率Preq、SOC 作为状态变量，燃料电池的输出功率Pfc、蓄电池的输出功率Pbat作为动作。由于单纯地将燃料电池系统消耗的氢气或者直接将蓄电池消耗的电能与耗氢量简单相加作为衡量燃料电池汽车经济性的标准，都不能真实地反映FCHEV能量的来源和使用的本质，因此,综合考虑FCHEV 的燃料经济性和维持SOC 的平衡，选定每一时刻氢气的实际消耗量mfc和蓄电池等效耗氢量mbat之和，以及引入SOC 惩罚函数作为回报函数，将需求功率转移概率作为状态转移概率。上述各变量表示为：

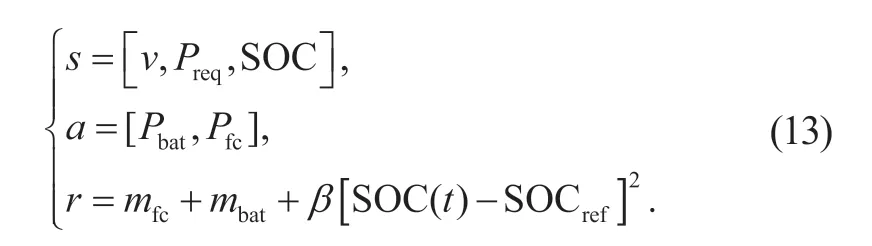
其中，s为状态变量；v为车速；Preq为整车需求功率；a为动作变量；Pbat蓄电池输出功率；Pfc为燃料电池输出功率；r为回报函数，为关于状态和动作的函数；mfc为氢气的消耗量；mbat为蓄电池的等效耗氢量；β为权重系数；SOC(t)为某一时刻蓄电池的荷电状态值；SOCref为蓄电池荷电状态的参考值。

为保证燃料电池汽车各部件能够正常工作，需要对以下参数进行约束:

其中：vmin、vmax分别为最低车速和最高车速；Pbat,min、Pbat,max分别为蓄电池的最小功率和最大功率；Pfc,min、Pfc,max分别为燃料电池的最小功率和最大功率；ΔPfc,min、ΔPfc,max分别为燃料电池输出功率的变化率下限值和上限值；SOCmin、SOCmax分别为蓄电池荷电状态的最小值和最大值。

2.2 构建目标函数模型

2.2.1 目标函数的建立

Q 学习算法是将状态-动作的累计回报的最小值作为优化的目标函数，可表示为

其中：π为策略，即在每个状态s下，指定动作a的概率。即根据已知的状态，由策略就能得到下一时刻的动作。γ为折扣因子，γ∈[0,1]。

将目标函数转化为Bellman 方程的形式

其中：Q*为最优Q值；P(s,a,s’)为转移概率矩阵，s′和a′为下一时刻的状态和动作。

由公式(16)可知，求解目标函数的关键在于对回报函数和状态转移概率的获得。

2.2.2 耗氢量及等效因子的求解

为了综合反映FCHEV 动力源的瞬时能量消耗水平，需要将燃料电池消耗的氢量与蓄电池耗电量归为统一的能耗指标。等效因子就是将蓄电池消耗的电能转化为耗氢量的转换系数，通过引入等效因子，将蓄电池提供给燃料电池汽车的能量转换为等效氢量，使得蓄电池的能量与燃料电池系统与氢气消耗量统一起来度量总的能量消耗。根据蓄电池放电和充电过程中能量转换的本质来构建充放电时等效因子模型。

当蓄电池处于放电状态时，SOC 值减小，为了维持SOC 的平衡，需要燃料电池对能量进行补充。图5为蓄电池放电时能量流动的等效模型图。其中，Pwh为传动车轮的功率；Pdc为转换器的输出功率；虚线部分表示未来时刻的能量流动路线，在未来某一时刻，燃料电池对蓄电池进行充电，增大燃料电池系统输出功率，通过DC/DC 转换器将电能传递给蓄电池，对蓄电池的电量进行补偿，使得SOC 值增大，来维持SOC 平衡。

图5 蓄电池放电时能量流等效模型

蓄电池放电时，由于补偿充电过程在未来状态下进行，燃料电池的工作效率、DC/DC 转换器效率和蓄电池的充电效率未知，因此，上述3 种效率都取均值。蓄电池放电能量与燃料电池补充的能量满足式（17）所示关系：

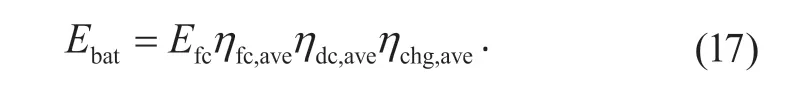
其中：Ebat为蓄电池提供的电能；Efc为燃料电池系统内部发生化学反应产生的电能；ηfc,ave为燃料电池的平均工作效率；ηdc,ave为DC/DC 转换器的平均效率；ηchg,ave为蓄电池的平均充电效率。

根据式(17)的能量守恒关系，单位时间内蓄电池放电时的等效耗氢量mbat可表示为

其中：Pbat为蓄电池的输出功率；ηdis为蓄电池的放电效率。

同理，蓄电池充电时能量流如图6 所示。蓄电池处于充电状态时，为了保持整个能量传递过程中的SOC 平衡，在未来时刻，蓄电池将会放电，为燃料电池汽车提供能量，即等同于未来将减少燃料电池的耗氢。其中，虚线部分表示未来时刻蓄电池消耗电能的能量流动路线。

图6 蓄电池充电时能量流等效模型

蓄电池充电时，由于电能消耗和减少燃料电池耗氢的过程在未来状态下进行，燃料电池的工作效率、DC/DC 转换器效率和蓄电池的放电效率未知，因此，上述3 种效率都取均值。蓄电池能量与燃料电池消耗的能量满足式（19）所示关系。

其中，ηdis,ave为蓄电池的平均工作效率。

根据式(19)的能量关系，单位时间内蓄电池充电过程中的等效耗氢量可表示为

其中，ηchg为蓄电池的充电效率。

将式(18)、(20)合并为

其中，λ为基于动力源能量流动平衡机理的等效因子，表示为：

2.2.3 需求功率转移概率的求解

车辆行驶过程中，由于实际工况存在着各种不确定性，会导致整车的需求功率Preq存在着随机性的变化，并且下一时刻的需求功率只与当前时刻的需求功率有关，而与之前的状态无关，因此可将车辆的需求功率视为Markov 过程，基于Markov 决策过程可以得到需求功率的转移概率矩阵。

选取城市循环+全球轻型汽车测试循环（urban dynamometer driving schedule+world light vehicle test cycle，UDDS+WLTC）工况作为求解需求功率转移概率矩阵的历史工况数据，将车速和需求功率进行离散化处理，得到整车需求功率时间序列如式（23）所示。

当车速为v时，由当前时刻的需求功率Pireq转移到下一时刻需求功率Pjreq时的状态转移概率Pij可表示为

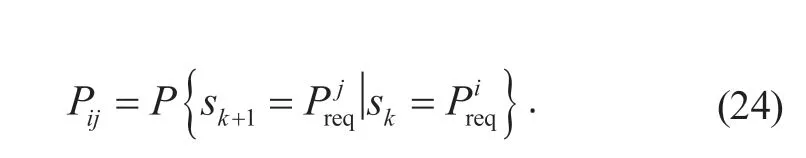
需求功率的转移概率可通过最邻近法和最大似然估计法进行求解。

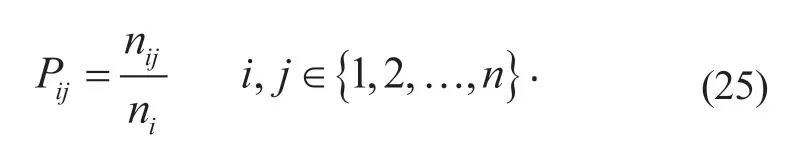
其中，nij为在已知的车速v下，需求功率由Pireq转移到的转移次数；ni为在车速v情况下，需求功率Pireq转移的全部次数。车速为15、35 km/h 时的需求功率转移概率分布如图7 所示。

图7 不同车速的需求功率转移概率矩阵

2.3 Q 学习算法能量管理策略的实现

基于Q 学习算法的燃料电池汽车能量管理策略主要分为离线优化和Simulink 在线仿真2 大部分，逻辑框图如图8 所示。

图8 基于Q 学习算法的燃料电池汽车能量管理策略逻辑框图

2.3.1 离线优化

变量设定及状态转移概率矩阵的建立。在Markov决策过程中确定状态v、动作a、回报函数r；通过利用典型行驶工况，求解需求功率的状态转移概率Pij，为离线优化过程做准备。

Q 学习算法迭代求解最优动作。Q 学习算法是将状态、动作对应的Q值储存在Q 表中，根据Q值的大小选择回报值最小的动作，通过不断地迭代学习，最终得到所有状态的最优动作。Q 学习算法流程图如图9 所示。

图9 Q 学习算法流程图

该算法的关键步骤可分为以下4 步，分别为：

第1 步，对状态-动作值函数Q(s,a)进行初始化处理，将Q 表中的数值全部设定为0。

第2 步，选择动作。在探索环境的过程中，为了避免在动作的选择过程中陷入局部最优，尽可能遍历所有动作，使得在利用和探索过程中得到平衡。采用ε-greedy 策略作为动作策略，使得在动作的选择过程中更倾向于选择状态-动作的累计回报趋向于最小值的动作。

第3 步，对策略进行改进。采用贪婪策略选择对应最小的状态-动作值函数Q(s′,a′)的动作a′。

第4 步，更新Q值。Q 学习算法采用一步预测的方法，对状态-值函数进行估计，状态-值函数的更新公式为

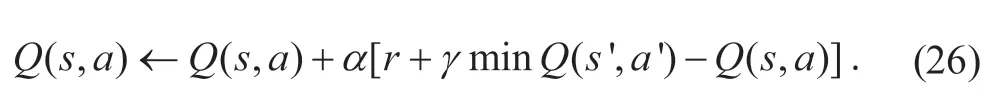
对上述过程进行循环迭代，将阈值设置为0.01来判断相邻迭代次数的Q值是否收敛，根据收敛后的Q(s,a)表，将最小的Q(s,a)值对应的动作确定为每个状态的最优策略。通过MATLAB/Simulink 仿真平台，建立基于Q 学习的能量管理策略仿真模型，在UDDS+WLTC 工况下进行离线仿真，对不同车速、需求功率和SOC 情况下的蓄电池、燃料电池输出功率进行最优解的求取，图10 为车速在15、25 km/h 时的蓄电池和燃料电池功率离线优化MAP 图。

由图10 可见，车速在15、25 km/h 时的蓄电池和燃料电池功率分配的趋势相同，并且SOC 对输出功率的分配影响不大，原因是当SOC 处于优化范围内时，功率的分配主要受到需求功率的影响。Q学习算法在优化动作时，将时域状态转化为空间域，功率的分配将会影响到燃料电池汽车的工作模式。当车速低，需求功率小时，一般由蓄电池提供动力；当需求功率增大时，由燃料电池提供能量。同时，在不同车速下的需求功率范围不同，车速越高，对应的需求功率范围就越大。

图10 不同车速下蓄电池和燃料电池功率优化结果

2.3.2 在线仿真

基于MATLAB/Simulink 平台建立了FCHEV 的前向仿真模型。分别将WLTC 循环工况和西宁市某路段实际工况数据作为输入，通过驾驶员模型获得加速或制动踏板开度信息，根据目标车速获得需求转矩，由电机及其控制器得到电动机的需求功率；通过将基于Q学习算法离线优化后的燃料电池、蓄电池的输出功率的Q 表嵌套到Simulink 在线仿真模型中，在线仿真验证本文所提出的能量管理策略的有效性和适应性。综合考虑当前车速、需求功率以及结合当前时刻SOC，采用在线查表的方式，得到每一时刻的蓄电池和燃料电池的输出功率，实时的获得最优的功率分配，将动力源的输出功率通过电动机转化为FCHEV 实际转矩、转速，通过主减速器模块、整车动力学模块获得当前实际车速，并反馈给驾驶员模型，实现FCHEV 在线仿真。

3 仿真结果分析

选取WLTC 工况和西宁市某实际路段工况分别对本文所提出能量管理策略的有效性和适应性进行在线仿真验证。

3.1 有效性验证

动态规划 (DP)算法通过逆向求解、正向寻优2 个过程获得全局最优的决策序列。在设计能量管理策略时，基于DP 算法的控制策略通常作为评价其他优化算法优劣性的基准[17-18]，因此本文选用基于DP 的控制策略和目前应用最广泛的基于规则的控制策略 (rule based,RB)与本文提出的基于Q 学习算法的控制策略(Q-Learning,QL)进行仿真对比，验证本文所提方法的有效性。

图11 为WLTC 循环工况，图12 是WLTC 工况下不同控制策略的燃料电池和蓄电池输出功率曲线。由图12 可知，在相同工况下，与RB 策略相比，QL 和DP策略能够更好地使燃料电池输出功率维持在高效率区域，有利于提高整车的经济性。由表2 给出了不同控制策略的百千米等效耗氢量对比结果。可以看出，本文所提QL 控制策略的等效耗氢量为0.730 kg/(100 km)，与RB 策略相比，耗氢量减少了8.57%，同时能够实现DP 策略93.59%的燃料经济性，说明了QL 策略具有较好的经济性，能够实现近似全局最优的效果。

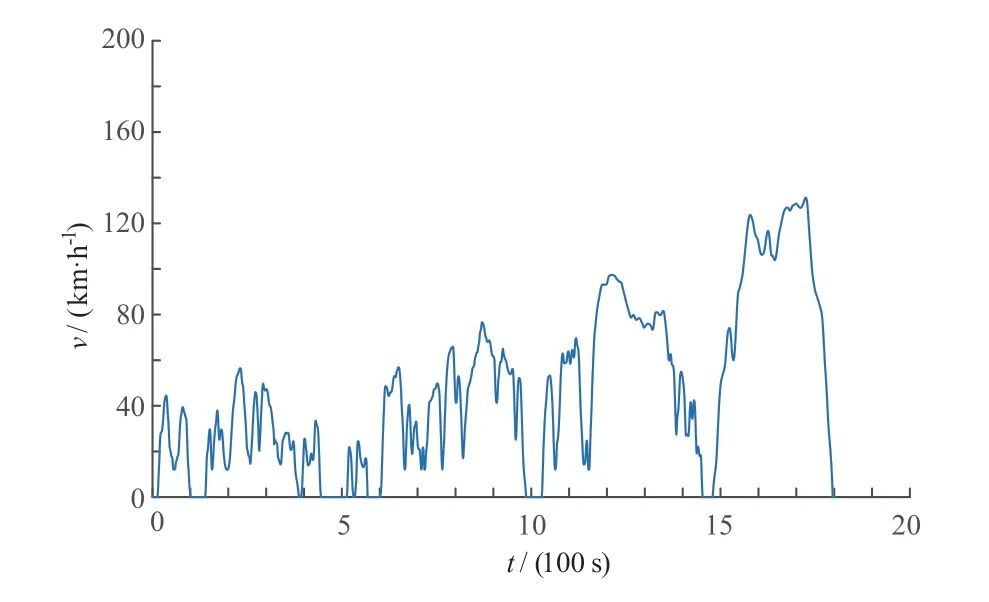
图11 WLTC 循环工况

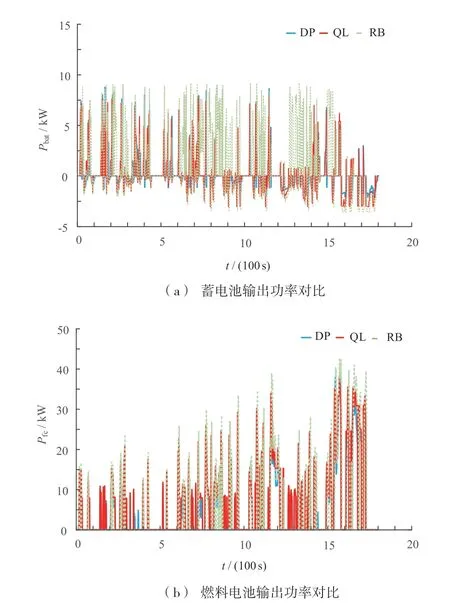
图12 WLTC 工况下燃料电池和蓄电池不同控制策略的输出功率对比

表2 WLTP 工况下燃料经济性对比

从图13 可以看出，基于RB 的策略下的电池SOC变化曲线下降比较明显，终端SOC 为0.578，没有很好的维持电池SOC 均衡。这是由于基于RB 的控制策略是通过专家经验来设置不同模式之间的切换规则，所设置的规则只是单一的将动力部件的工作点处于经济性较好的范围内，只追求经济性，对于SOC 的变化范围并未考虑。基于QL 的策略终端SOC 为0.594，十分接近初始值，表明SOC 在合理范围内波动，能够维持SOC 均衡，防止过充过放，延长电池使用寿命。究其原因在于基于QL 策略的回报函数中综合考虑了耗氢量和维持SOC 均衡，利用Q 学习算法来计算得到最优累计回报值对应的动作，该最优动作能在保证SOC 波动不致过大的情况下，最大限度的提高燃油经济性。以上对比结果证明了基于QL 的策略在维持SOC 平衡和提高燃料经济性方面具有较好的控制效果，验证了本文所提控制策略的有效性。

图13 WLTC 工况下的SOC 变化轨迹图

3.2 适应性验证

在UDDS+WLTC 工况下离线优化后，选取西宁市某路段作为实际工况，根据离线Q 表进行在线仿真，对比3 种算法（即基于动力源能量流动平衡机理的等效因子的动态规划算法(λvar-DP)、基于平衡机理的等效因子的Q 学习算法的控制策略(λvar-Q)、基于恒等效因子的Q 学习算法控制策略(λcv-Q)）的仿真结果，以验证本文所提λvar-Q 控制策略的工况适应性。

图14a 为西宁市某段实际工况，其主要包括城市工况和郊区工况2 部分,图14b、图14c 为基于3 种控制策略的蓄电池与燃料电池的功率分配曲线。表3 中列出了在西宁某路段实际工况下不同控制策略的燃料经济性对比数据。

图14 实际工况下不同控制策略蓄电池和燃料电池输出功率对比

表3 西宁某路段实际工况下燃料经济性对比

基于λvar-DP 策略与基于λvar-Q 策略进行对比,蓄电池的功率分配存在差异，燃料电池输出功率基本相同。主要是因为在城市工况，由于车速较低且存在频繁启停，蓄电池提供能量的次数增多，不同控制策略在动作的选择上存在差异，导致蓄电池的输出功率不同；在郊区工况下，车速较高且需求功率大，此时燃料电池处于高效率区域，由燃料电池单独驱动可获得更好地经济性，因此2 种策略都倾向于燃料电池单独驱动。由表3可知基于λvar-Q 策略的100 km 等效耗氢量为0.953 kg，能够获得较好的经济性，与离线优化工况下的耗氢量相近，验证了本文所提基于λvar-Q 策略的适应性。

基于λvar-Q 策略与基于λcv-Q 策略进行对比，由表3 可知基于λcv-Q 策略100 km 耗氢量为0.971 kg，本文所提基于λvar-Q 策略的100 km 耗氢量为0.952 kg，耗氢量降低2.02%。耗氢量存在差异的原因主要是不同等效因子对蓄电池的功率分配做出了调节。蓄电池的充放电效率会远远大于燃料电池的效率，在恒等效因子控制策略中对于能量的分配会更倾向于蓄电池提供能量，因此，从图15 可见，在蓄电池单独驱动或者混合驱动时，恒等效因子控制策略SOC下降趋势更明显，但燃料电池汽车蓄电池只是作为辅助动力源，对于能量的分配应该更多的倾向于燃料电池，由此可见本文所提出的基于λvar-Q 策略随着动力电池的充放电效率进行了实时调整，不断的对2 个动力源的能量分配进行权衡，从而更好地维持SOC 平衡，降低燃料的消耗，获得更好地经济性。

图15 不同控制策略SOC 变化曲线

4 结论

本文建立了燃料电池混合动力电动汽车能量管理的控制模型，构建了等效耗氢量最小及荷电状态（SOC）平衡的目标函数，并详细阐述了燃料电池耗氢量与蓄电池电量消耗和补偿的能量转化平衡机理并由此构建了等效因子模型。提出了一种基于Q 学习算法的能量管理策略，在UDDS 和WLTC 工况下，得到不同车速下的需求功率转移概率矩阵，通过离线优化的方式获得燃料电池和蓄电池的最优功率分配。最后在WLTC工况下进行仿真验证，结果表明，本文所提出的控制策略能够维持SOC 平衡，且与基于规则的控制策略相比经济性提高了8.57%，并能够达到DP 控制策略的93.59%的经济性，验证了本文控制策略的有效性。在西宁市某实际工况与动态规则（DP）和基于恒等效因子的控制策略进行对比仿真，所提的控制策略100 km 耗氢量为0.971 2 kg，与恒等效因子策略相比耗氢量减少2.02%，说明所提策略对经济性有所提高；与基于DP控制策略的耗氢量接近，验证了提出的基于等效因子的Q 学习算法的适应性。