考虑因素交互作用的车—车事故严重程度分析
2022-02-01张道文王朝健黎华惠
张道文 ,王朝健,蒋 骏,黎华惠
(1.西华大学 汽车与交通学院,成都 610039,中国;2.汽车测控与安全四川省重点实验室,成都 610039,中国;3.四川省新能源汽车智能控制与仿真测试技术工程研究中心,成都 610039,中国;4.成都工业职业技术学院,成都 610218,中国)
2020 年,中国大陆机动车导致的交通事故数达21.1 万起,造成5.6 万人死亡、21.4 万人受伤和12.28亿元直接财产损失[1]。交通事故可以分为车与人事故、车与二轮车或三轮车事故以及单车事故(即本车事故)、车对车(V2V)事故(以下又称双车事故)、多车事故。V2V 事故严重程度不仅取决于己方驾驶员和车辆的特征,还取决于对方驾驶员和车辆的特征[2],且V2V 事故的占比高于其他事故类型[3]。因此研究双车事故严重程度的关键因素,以及因素的交互作用对致死事故率的影响,对预防V2V 事故和降低驾乘人员的伤亡具有重要意义。
对V2V 事故的研究主要基于Logit 模型(Logit model)、Probit 模型(Probit model)等线性模型而限制了逻辑相关变量的引入。C.Duncan 等[4]采用有序Probit 模型(ordered Probit model),研究了V2V 事故中乘用车驾驶员损伤严重程度的影响因素。G.A.Torrão 等[5]采用Logit 模型发现了V2V 事故中,对方汽车的发动机排量是重要影响因素。贾雄文[3]利用二项有序Probit 模型(bivariate ordered Probit,BOP),研究了国内V2V 事故受伤严重程度的关键影响因素。随后贾雄文等[6]利用BOP 模型,研究了道路环境因素对V2V 事故严重程度的影响,发现道路等级的提升会降低驾驶员的受伤程度。蒋欣国等[7]利用广义有序Logit模型(generalized ordered Logit),研究了双方驾驶员的危险行为对V2V 事故的影响,发现超速和其他行为同时存在时对事故后果有显著影响。王健宇等[8]基于多项Logistic 回归模型(multinomial Logistic regression,MNL),研究了V2V 事故严重程度的影响因素及机理,探索了在不同严重程度的交通事故中影响因素存在的差异性。一些学者研究V2V 事故时,驾驶员因素一般仅考虑了受伤更严重的一方驾驶员;主要基于单因素分析,没有考虑因素的交互作用,而交通事故是多风险因素对事故伤亡的综合效应。
针对因素交互作用对事故严重程度的研究,有学者利用Shapley 加和解释(Shapley additive explanations,SHAP)结合XGBoost[9]、LightGBM[10]等模型,但这种方法只能分析2 个因素的交互效应对事故后果的影响趋势,不能量化分析[9]。有学者提出利用N-K 模型量化多种因素的交互作用对事故后果的影响[11],但N-K模型只能解决因素之间的整体交互效应,不能分析因素具体状态值的交互效应。有学者利用故障树[12]、关联规则[16]提取具有强耦合度的规则,但这些方法也不能具体量化规则对事故后果的影响程度。
Bayes 网络(Bayesian networks,BN)模型具有高解释度的优势,已应用于交通安全的研究[14]。它能量化单因素以及多因素的交互作用对事故后果的影响,但多因素分析时,会面临因素组合过多、主观定义的组合耦合度低甚至为不可能事件等问题,而关联规则刚好能弥补这一缺陷。
本文运用Bayes 网建立考虑风险因素交互作用的V2V 事故严重程度模型。定量分析关键影响因素、双因素的交互作用对致死事故率的影响,结合关联规则方法挖掘高频率和强耦合度的规则,探究多因素交互作用下对致死事故率的影响,以期明确V2V 事故的预防重点,从而实施精准的防控策略。
1 方 法
1.1 Bayes 网络
Bayes 网络(BN)是一种描述变量间不确定因果关系的网络模型,能很好地捕捉变量之间的潜在影响关系,有结构学习和参数学习2 个部分。当随机变量有n个时,变量之间的关系可以由一个联合概率分布表示:
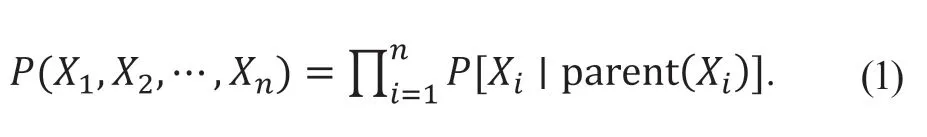
式中:X1、X2、…、Xn为随机变量;parent(Xi)为随机变 量Xi的全部父节点集合。当(parent(Xi)=ø 时,parent[Xi|parent(Xi)]是边缘分布P(Xi)。
结构学习中,增强朴素Bayes(augmented naive Bayes,ANB)算法克服了传统朴素Bayes 算法中因素局部独立性的限制、应用广泛[15]。完整数据的参数学习通常利用最大似然估计,定义如下:
P(|θ=θ0)表示参数θ的某个取值θ0与数据的拟合程度,取值越大说明θ0与数据的拟合程度越高。给定θ,数据的条件概率P(|θ)称为θ的似然度:
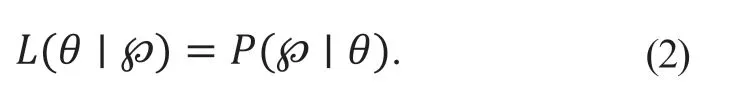
令L(|θ)达到最大值时的取值θ*为参数θ的最大似然估计(maximum likelihood estimation,MLE):
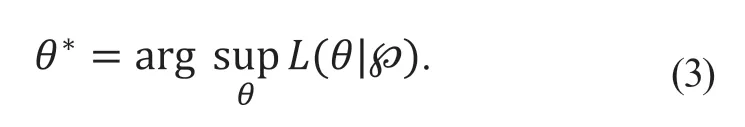
1.2 关联规则
关联规则算法可以挖掘要素之间的内在联系,用X≥Y表示,X为前项,Y为后项。一般有支持度和置信度2 个衡量指标。
支持度指X和Y的同时出现的概率,用support(X≥Y)表示,置信度指出现后,出现的概率,用confidence(X≥Y)=P(Y|X)表示。支持度越高表示前项出现的概率越高,置信度越高代表前项发生,后项出现的概率越高[16]。
1.3 验证
常用的验证方法有K折交叉验证、接受者操作特性曲线(receiver operator characteristic,ROC 曲线)和ROC 曲线下的面积(area under curve,AUC)。K折交叉验证将数据集划分为K个大小相等的部分,K-1 部分用于训练,最后K个部分用于测试,这个过程重复K次[15]。留一法(leave one out,LOO)是K折交叉验证的极端情况,它将数据集的n-1 条数据用于训练,最后一条数据用于测试,这个过程重复n次,验证过程没有随机因素的影响,结果稳定[17]。
2 数据处理及模型建立
2.1 数据处理
(中国)国家车辆事故深度调查体系(national automobile accident in-depth investigation system,NAIS)由(中国)国家市场监督管理总局缺陷产品管理中心联合中国8 所高校、多家交通司法鉴定中心共同建立[18]。事故数据覆盖了中国大陆7 个地域,已有学者利用该数据库进行了相关研究并取得了成果[19-21]。
对样本进行以下初步筛选:
1)剔除由于研究对象为V2V 事故,需涉及行人、机动二三轮车、非机动二三轮车、V2V 和多车的事故;
2)剔除与研究无关的字段,同时剔除剩余字段中不完整的数据;
3)由于高速公路为封闭式道路管理,有别与其他道路,因此剔除涉及高速公路的案例[22];
4)删除剩余事故中的特殊案例,例如静止车辆由于制动失效导致的事故、车辆自燃导致的事故。最终剩下583 例事故。
2.2 变量选取
交通事故的影响因素众多,总体可分为人、车、路和环境4 个方面。人的方面主要包括驾驶人的心理因素和生理因素,例如驾驶人的年龄、性别和状态等因素会影响驾驶员的感知能力和反应能力;车是人的载体,车辆的类型和安全技术状况会间接影响事故后果,而驾驶人对车辆的控制会直接影响车辆的运动状态;道路是交通的载体,主要包括发生地点、行政等级和路面状况等因素;环境通过影响人、车和路方面而间接影响事故的发生,一般指自然环境的因素,例如天气状况、事故发生的时段。
考虑以往研究的变量选取并结合NAIS 数据库的字段特征,从人、车、路和环境4 个方面选取17 个变量(包括影响因素和事故严重程度)[3,6,11,27],分为过失方因素(L1-L5)、受害方因素(I1-I5)、道路因素(R1-R4)、环境因素(E1-E2)和事故严重程度(Sev),各变量取值及离散情况见表1。
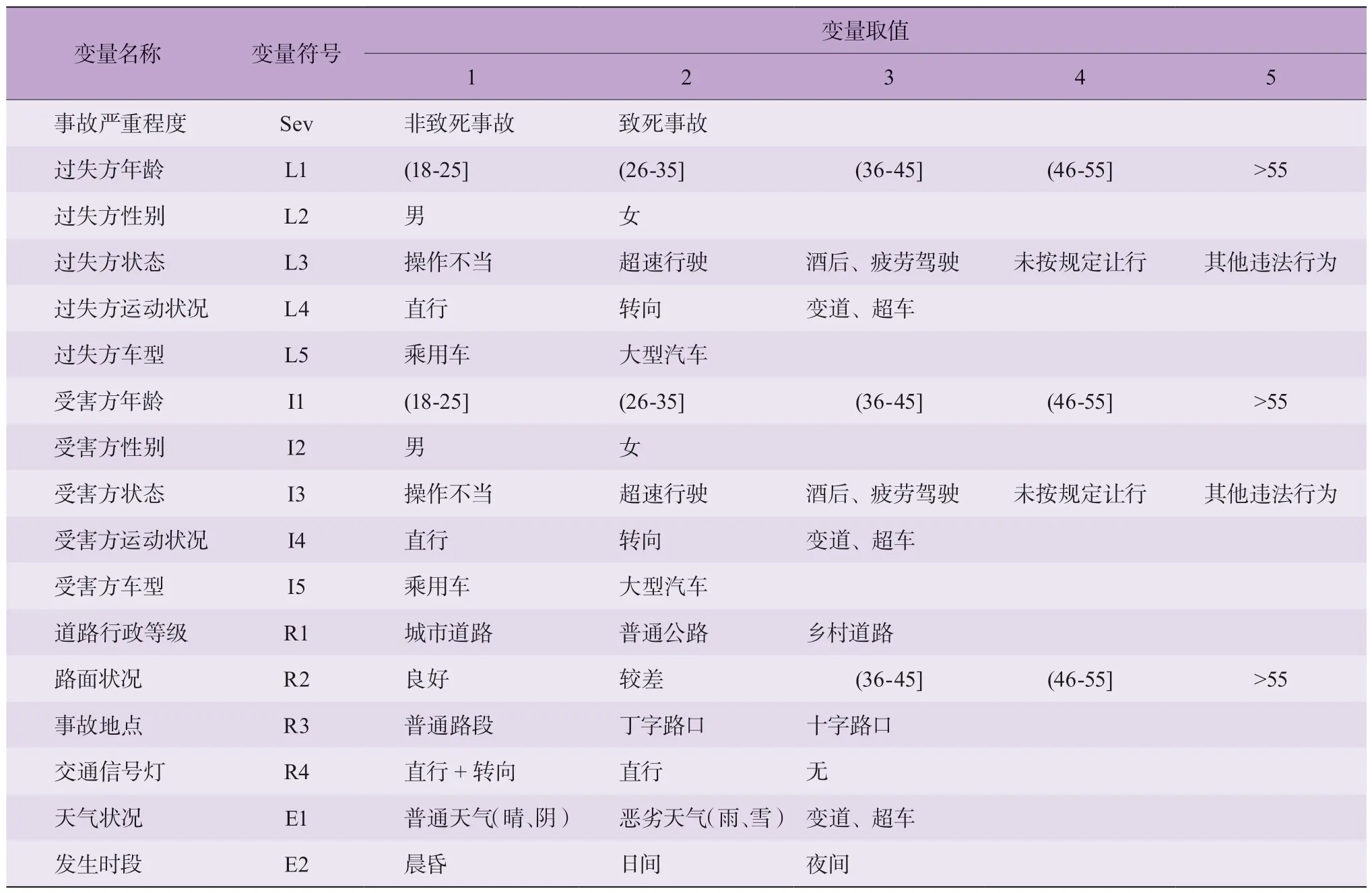
表1 变量取值及离散情况
2.3 结构建立
运用GeNIe3.0 软件进行结构学习和参数学习,得到V2V 事故严重程度分析模型的Bayes 网络结构图,一共包括17 个节点和29 条边,如图1 所示。其中:每一个节点代表一个变量,节点之间的连线代表变量之间具有直接依赖关系,如天气状况(E1)与路面状况(R2)有直接依赖关系。
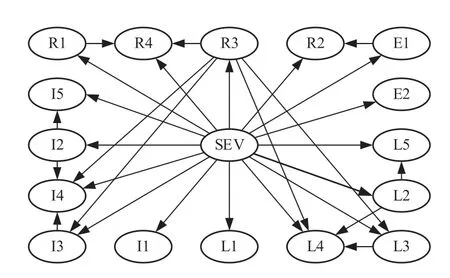
图1 Bayes 网络结构图
2.4 模型验证
利用留一法进行模型验证,模型的准确率为81.3%,若准确率达80%,代表预测效果较好[24]。ROC 曲线下的面积(AUC)为0.81,表明算法的鲁棒性较好,因此V2V 事故严重程度分析模型较合理。接受者操作特性曲线(ROC 曲线)和AUC 如图2 所示。
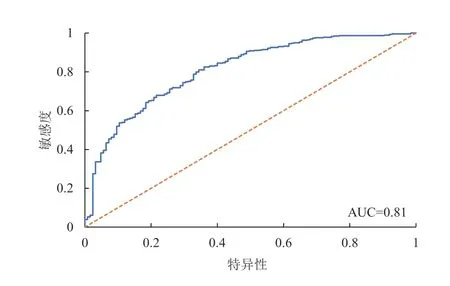
图2 ROC 曲线和AUC
3 推理分析
3.1 关键因素分析
为探究事故严重程度的关键影响因素,基于Bayes网络构建的分析模型,输入每个变量的各个取值状态(对于每一个变量,其中一个取值的概率被设置为100%,同一变量的其他取值被设置为0%,例如过失方性别为男性,则女性的概率为0%),然后更新整个模型,观察该变量的不同取值下致死事故率的变化。其中每个变量的不同取值状态对致死事故率的最大影响幅度见表2。
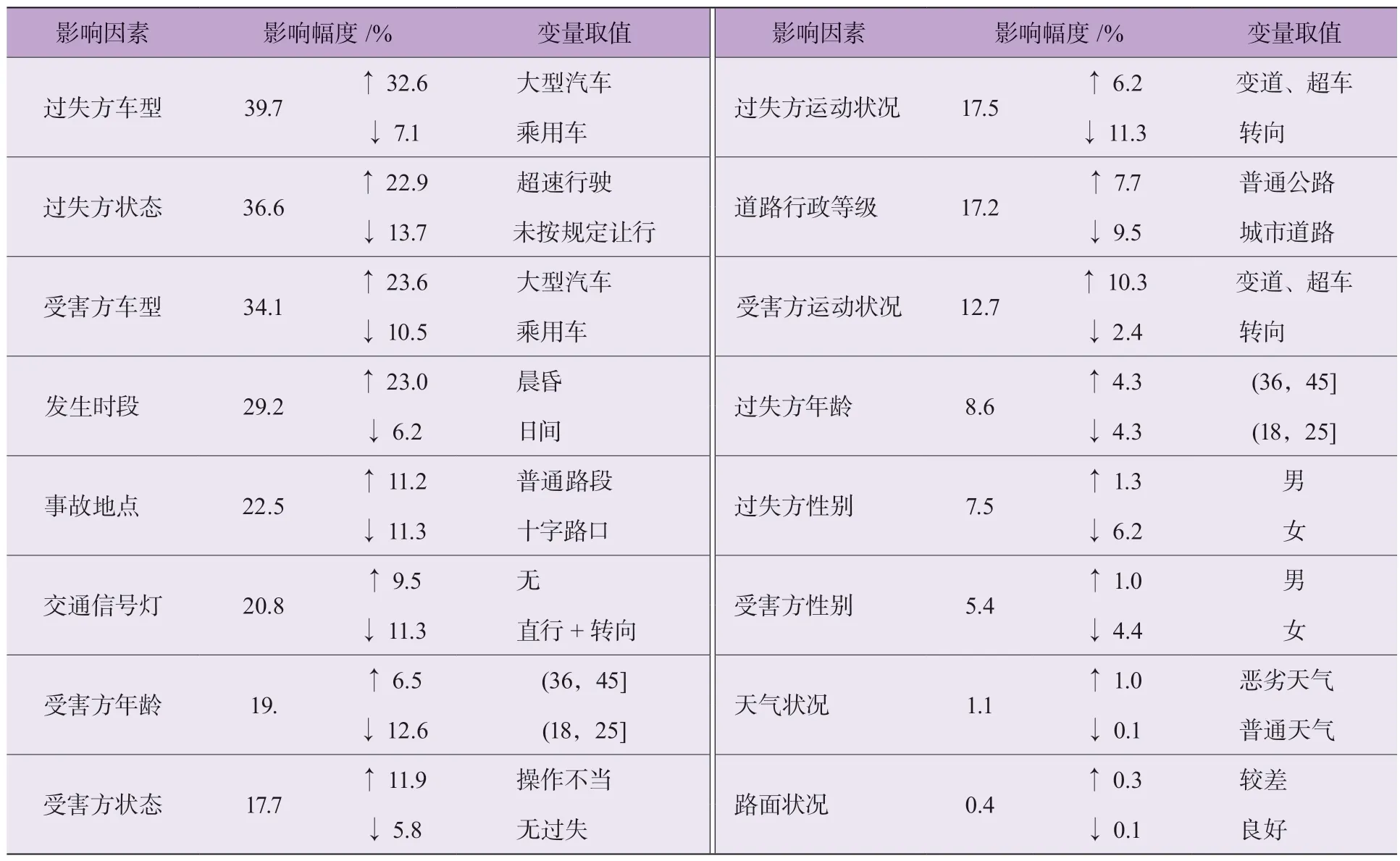
表2 各因素对致死事故率的影响幅度
“↑”代表取值对致死事故率的最大增幅;“↓”代表取值对致死事故率的最大降幅。例如过失方车型(因素L5)对致死事故率的影响幅度为39.7%,其中大型汽车因素会提高32.6%致死事故率(后文涉及的提高与降低均是相较于致死事故率的先验概率),乘用车因素会降低7.1%致死事故率。
由表2 可知,L5、L3、I5、E2、R3、R4 等因素对致死事故率的影响幅度均超过20%,是引发致死事故的关键因素。过失方或受害方为大型汽车、过失方超速行驶会显著提高致死事故率[7];调整模型发现夜间(4.5%)的致死事故率高于日间[25]。发生在晨昏的事故占比仅6%,但该时段一旦发生事故,致死事故率会提高23%,相反发生在日间的事故占比最高,但致死事故率会降低6.2%。可能是晨昏车流量小,驾驶员警惕较低,导致行驶速度较快,而日间车流量大且行车视距较好,驾驶员更加谨慎[3];普通路段和十字路口的事故占比较高,但十字路口比普通路段的致死事故率低22.5%[23];设立信号灯能降低致死事故率,设立直行+转向交通信号灯路段比无交通信号灯路段的致死事故率低20.8%,这是因为交通信号灯对驾驶员有警示作用,能降低交通冲突程度[23]。
(36,45]岁的驾驶员会略微提高致死事故率,而(18,25]岁的驾驶员会降低致死事故率。Lee C[25]指出30 岁以下的年轻司机在碰撞中受伤程度会降低,并且(18,25]岁的青年驾驶员由于驾驶经验不丰富,警惕性反而更高;过失方或受害方的转向行为均会降低致死事故率,但过失方的转向行为降低幅度更大,可能是因为过失方处于转向时,能更好的提前发现碰撞目标,实施主动避险行为;普通公路比城市路段的致死事故率高17.2%。男性驾驶员、恶劣天气和较差的路面状况等因素都会提升致死事故率,但影响程度较小。
3.2 二维推理分析
为考察双因素的联合效应对致死事故率的影响,以致死事故率的影响幅度中最大的因素L5 与其余关键因素进行组合分析,观察2 个变量的不同取值组合的致死事故率,各组合的联合效应见图3。其中纵坐标底部为过失方车型的变量取值,纵坐标中部为其余关键因素的变量取值,横坐标为该组合的致死事故率。
由图3 可知:因素交互作用下,因素的联合效应显著。例如相较于过失方为乘用车,过失方为大型汽车与其余关键因素的交互作用更容易引发致死事故,尤其是驾驶员处于超速行驶或处于晨昏时段,因此建议大型汽车强制装配超速报警装置,并且驾驶员在晨昏等光线不好的环境要提高驾驶警惕;因素的联合效应影响高于各自边际效应之和。例如过失方为大型汽车且发生于普通路段时,致死事故率提高的边际效应之和为42.1%,而联合效应之和为44.4%。
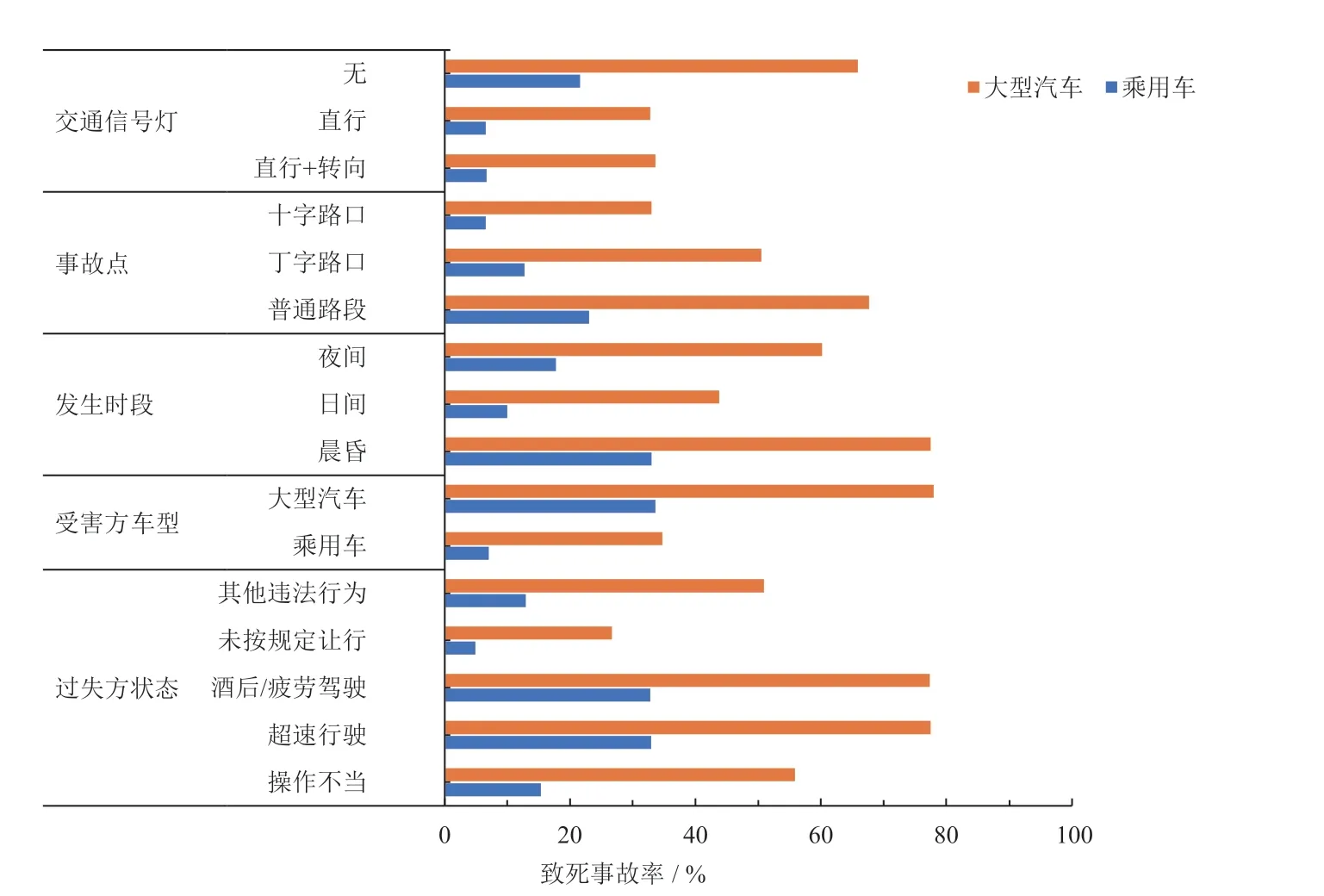
图3 过失方车型和其余关键因素的联合效应
3.3 多维推理分析
交通事故是多风险因素对事故伤亡的综合效应,但面临因素取值的组合过多、主观定义的组合耦合度低甚至为不可能事件等问题。因此利用SPSS Modeler软件的关联规则挖掘关键因素中高频率与强耦合度的规则,将关联规则输出的规则中各个变量的取值,作为Bayes 网络分析模型中每个变量的输入,计算各个规则的致死事故率的变化。为了挖掘高频率和强耦合度的规则,设定最低支持度为20%和最低置信度为80%,剔除前后项内容相同的规则后,最终得到10 条规则见表3。
表3 可知:规则1 的支持度最高,说明该组合出现的频率较高,但此时致死事故率会下降18.3%。这和C.Lee[25]结论类似,小型车之间的碰撞增加了非致死事故率,并且车辆在通过交叉口时的车速较低,因此降低了致死事故率[26];规则2 出现的频率较高,会小幅度提升致死事故率;与规则2 类似的是规则5,但规则5 发生时会增加42.6%的致死事故率,这是由于受害方为大型汽车时,尽管会降低受害方驾驶员的致死率,但会显著提高过失方驾驶员的致死率[23];规则7是唯一含夜间的高耦合规则,这种事故容易发生在无交通信号灯的普通路段,并会提高21.7%的致死事故率。这极大可能是因为夜间车流量低、无交通信号灯的警示,并且普通路段的干扰小,此时汽车的行驶速度较快,加上夜间视野差,导致发生紧急情况时驾驶员的避撞时间不足。
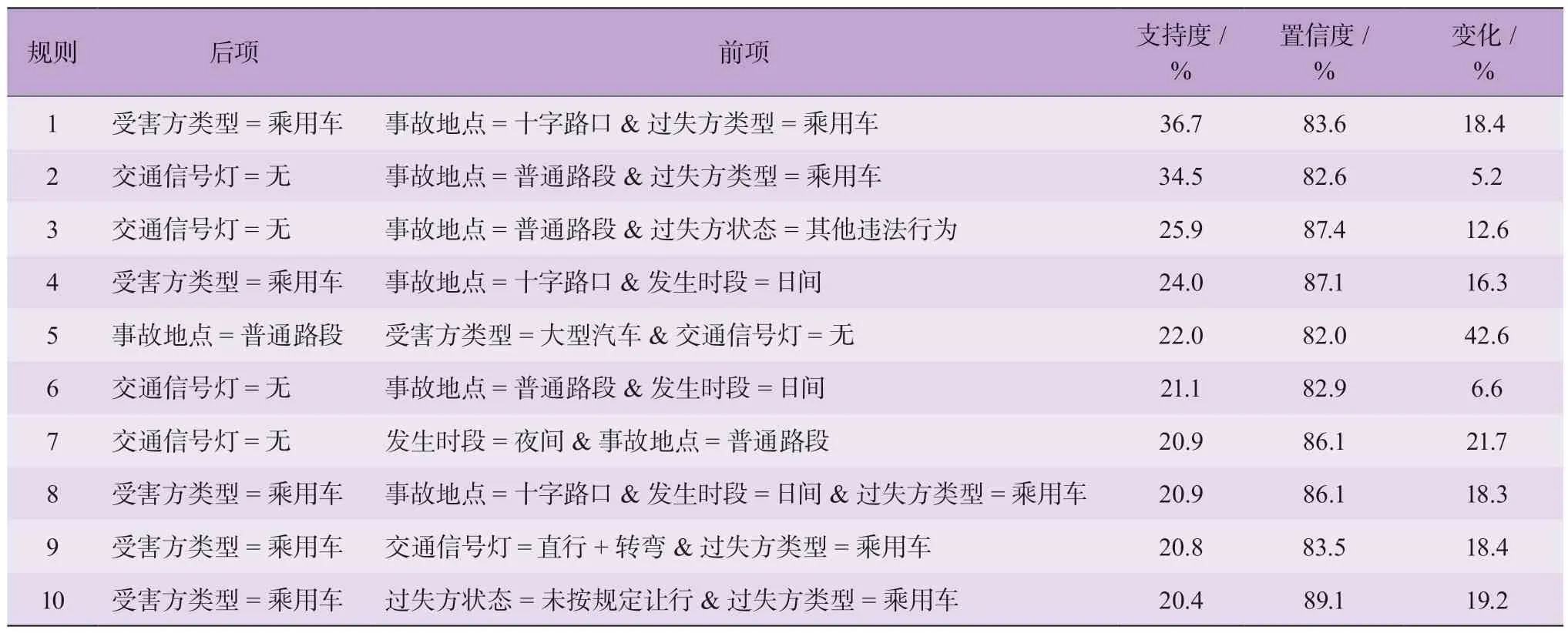
表3 高频率与高耦合规则集对致死事故率的影响
4 结论
本文以NAIS 数据库的双车事故为样本,利用Bayes 网络和关联规则方法,研究了V2V 事故严重程度的关键影响因素,以及关键因素的交互作用对致死事故率的影响。主要结论如下:
1)过失方车型、过失方状态、受害方车型、发生时段、事故地点、交通信号灯等因素,是致死事故率的关键影响因素。
2)因素交互作用下,因素的联合效应显著,并且影响高于各自边际效应和。过失方为大型汽车且处于超速行驶会提升55%的致死事故发生率,因此建议大型汽车强制装配超速报警装置;驾驶员在晨昏时段,要提高驾驶警惕。
3)在十字路口两辆乘用车发生事故的频率较高,但致死事故率相较于致死事故率的先验概率会降低18.4%;大型汽车在无交通信号灯的普通路段发生事故,会提高42.6%的致死事故率。
4)数据采集的困难导致数据和字段有限,没有充分考虑到车流量、汽车安全状况和管理方面等因素,可能会对研究结果产生一定影响,有待进一步研究。
