UHPC中PBL剪力键力学性能试验研究

2022-02-01肖林，廖轩，卫星，陈飞

铁道学报 2022年12期

肖林，廖轩，卫星，陈飞

(西南交通大学土木工程学院，四川成都 610031)

PBL剪力键是钢-混组合桥梁中使用的主要剪力连接件形式之一，因弹性受力阶段刚度大，塑性受力阶段延性好的特点被广泛应用于大跨度混合桥梁的钢-混结合段中[1-3]。影响PBL剪力键力学性能的因素较多，其中混凝土的材料特性是关键因素之一[4-5]。近年来，UHPC因其高抗压强度、高韧性、高耐久性等特点在钢-混组合桥梁中的应用方兴未艾，将PBL剪力键与UPHC配合使用有望进一步提高其力学性能。

目前学术界开展了HPC中PBL剪力键的力学性能研究[6-8]，通过推出试验探索了现浇HPC桥面板中PBL剪力键的力学性能和破坏形态，分析了钢板开孔直径、贯穿钢筋直径等构造参数对剪力键性能的影响。关于UHPC中PBL剪力键的少量研究也集中在UHPC桥面板中PBL剪力键的力学行为上[9-10]，通过一定数量的推出试验研究了剪力键构造参数、钢混界面黏结、钢纤维含量以及横向钢筋对剪力键力学行为的影响。既有研究成果加强了对于桥面板中浅埋PBL剪力键力学性能的认识，但尚不足以用于指导UHPC桥面板中PBL剪力键的设计。而PBL剪力键良好的抗剪刚度与承载力使得其更适用于混合桥梁中的钢-混结合段中，在钢-混结合段中的PBL剪力键的力学行为可能与桥面板中浅埋剪力键存在差异[11]，但目前对深埋UHPC中PBL剪力键的相关研究尚处于空白。

本文通过两组推出试验研究了UHPC中PBL剪力键的破坏模式、荷载-滑移曲线、应变发展等行为，并分析了其承载力、抗剪刚度等力学性能，评估了既有PBL剪力键的承载力计算公式的适用性。

1 推出试验方案

1.1 试验模型设计

考虑到钢-混结合段中PBL剪力键的受力特征与标准推出试验不完全一致[12-13]，且为便于与以往研究结果对比[10-12]，本文推出试验采用“三明治”构造，见图1。

图1 UHPC-PBL剪力键推出试验构造

两组试件中，UPT1试件包含1个PBL剪力键，UPT6试件包含6个PBL剪力键。试件构造参数见表1，模型尺寸见图2。

表1 推出试件规格表

图2 试验模型

模型中开孔钢板材质为Q345qB，普通钢筋、贯穿钢筋材质采用HRB335。混凝土为商用UHPC-120，通过试验测得其立方体抗压强度为127.2 MPa，抗拉强度为6.5 MPa，弹性模量为42 319 MPa。

1.2 加载、测试方案

对每个试件分别进行设计承载力、极限承载力两种工况的加载试验。

加载前需要确定试件的理论承载力值，以便设置合理的加载等级。文献[14]在总结国内外试验研究成果的基础上给出了开孔板连接件的承载力设计值计算式，较全面地考虑了剪力键承载力的影响因素，并且留有一定的安全储备。本文采用该公式计算试件设计承载力F。

每个试件在加载前均以0.2F进行3次预加载，每次持荷5 min，以消除开孔钢板与UHPC间的界面黏结力。

设计承载力加载工况中，采用荷载控制分级加载，每级荷载增量20 kN，持荷5 min，加载至设计承载力F后按50 kN分级卸载。

极限承载力加载工况中，先以20 kN荷载增量分级加载至设计承载力F，然后采用位移控制加载至试件破坏。各级位移增量为0.2 mm，加载速率为0.2 mm/min，每级持荷载5 min或直至结构响应稳定。

测点布置见图3。试验测试内容主要包括试件承载力、钢-UHPC相对滑移、贯穿钢筋应力以及UHPC的应力。试件承载力由压力机自带压力传感器获取；采用千分表测量焊接在开孔钢板两侧的相对变形钢筋与混凝土块的竖向位移，获得剪力键的相对滑移；贯穿钢筋与UHPC应力采用应变片测试，其中贯穿钢筋应力测点位于其中心点左右两侧各32 mm处，在每根贯穿钢筋上左右、上下对称布置4个测点。

图3 应力与相对滑移测点布置

2 推出试验结果

2.1 试件破坏过程与破坏形态

试件表面破坏形态见图4。由图4(a)可见，加载时裂缝首先出现在UHPC块外侧中部；随着荷载增加，裂缝以不同发展速率分别向上、下延伸，裂纹宽度逐渐扩大，钢纤维从UHPC中被拔出或拉断，但未出现新的裂缝，期间钢与UHPC相对滑移持续稳定增长。试件加载后期，相对滑移快速增加，试件表现出良好的延性。最终破坏形态为贯穿钢筋剪断，而UHPC除外侧竖向裂缝外，其余部分完好，能对剪力键形成有效的包裹作用。

由图4(b)可见，对于多剪力键的UPT6试件，UHPC表面裂缝宽度更小，裂缝发展更为缓慢。在加载后期，第1排剪力键首先被剪断，此时第2、3排剪力键仍能继续承载。

图4 试件表面破坏形态

加载完成后沿垂直方向切开已破坏的试件，观察其内部破坏形态，发现孔内贯穿钢筋上部的UHPC榫被压碎成白色粉末，下部有少量UHPC榫从界面剥落，但贯穿钢筋基本位于钢板孔洞中间，孔内UHPC未发生塑性流动。孔洞内混凝土的破坏情况见图5。

图5 开孔钢板孔洞内混凝土榫破坏形态

试件破坏后开孔钢板的两组试件的开孔钢板均保持完好，孔壁均未发生变形。

贯穿钢筋被剪断后的变形形态见图6。由图6可知，UPT1中贯穿钢筋的弯曲变形很小，在钢板与UHPC界面处有较大的剪切变形，其破坏模式以剪切破坏为主；UPT6中贯穿钢筋发生一定程度的弯曲变形，且断口附近出现明显颈缩现象，破坏模式为拉剪破坏。

图6 试件破坏后的贯穿钢筋形态

PBL剪力键的传力与破坏机理见图7。由图7可知，混凝土榫受到钢板，贯穿钢筋以及周围混凝土的约束限制，所形成的三轴压缩区将开孔钢板上的荷载扩散至贯穿钢筋的弯曲区域。

图7 PBL剪力键的传力与破坏机理

普通混凝土中的PBL剪力键失效时，由于混凝土强度相对钢材低，混凝土榫易被压碎并在剪力键核心受力区发生塑性流动，导致贯穿钢筋被挤到开孔钢板边缘与钢板接触，若贯穿钢筋直径较小则可能被开孔钢板剪断，若开孔钢板较薄则有可能被贯穿钢筋撕裂[11]。当发生贯穿钢筋被剪断时，钢筋往往会产生明显的弯曲变形。

UHPC强度高、弹性模量大，在剪力键破坏时，UHPC榫压碎区域相对较小，钢筋受弯曲域变小，荷载更加集中，从而导致贯穿钢筋弯曲变形较小。由于钢纤维的桥接作用，被压碎的UHPC仍能有效包裹贯穿钢筋，将开孔钢板上的荷载分散至贯穿钢筋，最终贯穿钢筋被剪断。

2.2 荷载-应变曲线

图8 应力测点布置

图9 贯穿钢筋荷载-应变曲线

由图8可知，贯穿钢筋中应变片沿钢筋轴向布置，以监测贯穿钢筋发生轴向变形或弯曲变形时的应力状态。由图9可知，在UPT1试件的加载初期，贯穿钢筋基本无应变，表明此时贯穿钢筋保持平直状态，主要是UHPC榫承担荷载；随着荷载增加UHPC榫逐步失效，在孔内的贯穿钢筋开始发生弯曲、剪切变形；当UHPC榫剪断后，原本由UHPC榫承担的荷载转由贯穿钢筋分担，贯穿钢筋受力类似于支撑在两端UHPC块上并承受开孔钢板集中荷载的弹性地基梁，加载点处的弯曲应变持续增大。对于UPT6试件，第一排剪力键承担荷载最大，其贯穿钢筋的应变发展最快，第二排剪力键次之、第三排最小。

2.3 荷载-滑移曲线

各试件的荷载滑移曲线见图10。由图10可知，剪力键的受力过程可分为弹性阶段、弹塑性阶段、屈服阶段。在弹性阶段，同组试件的荷载-滑移曲线非常接近，其他阶段各试件试验结果的离散性较小。由于UHPC无粗骨料，材料性能较为均匀，作为PBL剪力键主要传力构造的UHPC榫力学性能较稳定，因此同组试件剪力键的力学性能差异较小。

图10 荷载-滑移曲线

在弹性阶段UHPC榫尚未发生剪切破坏，试件主要依靠UHPC榫与贯穿钢筋共同传递剪力，抗剪刚度较大；随着荷载增加，UHPC榫内产生剪切裂缝，剪力键进入弹塑性阶段，试件抗剪刚度降低；UHPC榫被剪断后试件进入屈服阶段，UHPC榫所承担的荷载转由贯穿钢筋承载，剪力键相对滑移量迅速增加，刚度明显下降。UPT1与UPT6两组试件的极限滑移量比较接近，均在16 mm左右，并表现出较强的延性。UPT6的极限承载力约为UPT1的2.6倍。

UPT6试件使用了3排6个PBL剪力键，各排剪力键的相对滑移曲线比较见图11。由图11可知，承载时自上往下第一排剪力键滑移量最大、第二排次之、第三排最小，假定各排剪力键刚度相同，则第一排剪力键承担的荷载最大、第三排剪力键承担的荷载最小。

图11 UPT6各排剪力键的荷载-滑移曲线

2.4 荷载、滑移与应变的关系

加载过程中剪力键的荷载、滑移与贯穿钢筋应变的关系见图12，图12中UPT6取其第一排剪力键中贯穿钢筋的应变。由图14可知，在加载初期，贯穿钢筋应变增长滞后于相对滑移，进一步说明在加载初期UHPC榫的变形是造成相对滑移的主要原因。

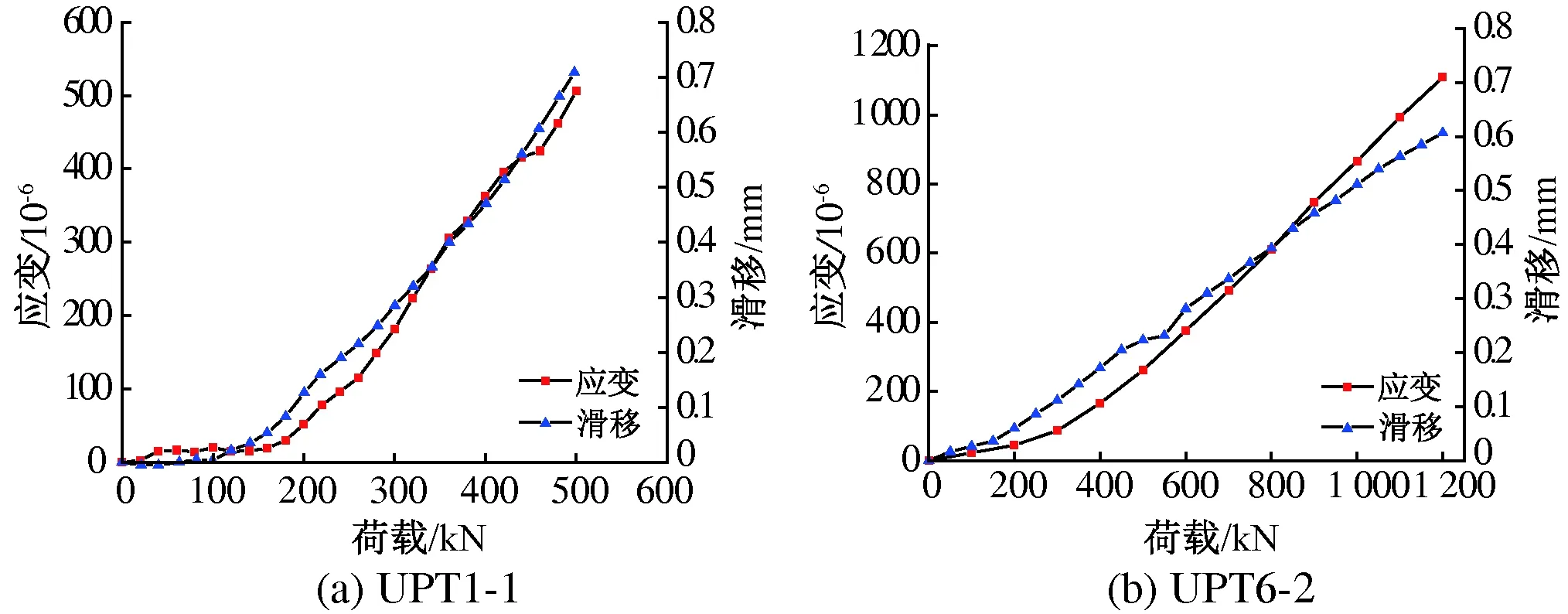
图12 荷载与相对滑移、贯穿钢筋应变曲线

剪力键的相对滑移与贯穿钢筋应变的关系曲线见图13。由图13可见，当相对滑移量小于0.2 mm时，两组试件贯穿钢筋的应变基本保持不变或增长缓慢，此时主要是UHPC榫承担荷载。随着荷载增加，UHPC榫失效后贯穿钢筋成为承担荷载的主要构件。

图13 滑移与贯穿钢筋应变曲线

从剪力键试件的微观行为(构件应力状态)中可发现：剪力键初期的承载能力与滑移能力主要体现在UHPC榫的抗剪切能力与变形能力上；随着UHPC榫剪切裂缝的产生，贯穿钢筋逐步承担更多荷载，成为主要受力构件；发生剪切破坏的UHPC榫主要起到包裹钢筋、分散传力的作用，剪力键的极限承载力则主要由贯穿钢筋的抗剪能力决定，钢筋下方的UHPC块提供一定刚度的支撑作用。

马略卡岛(Mallorca)位于地中海，面积3640平方公里(南北75公里、东西100公里)，马略卡岛首府帕尔马。马略卡岛上到处是砂质的海滩、陡峭的悬崖、种植着橄榄或是杏树的田野等自然风光。

3 UHPC中PBL剪力键的力学性能

3.1 评定指标

为研究PBL剪力键在UHPC和普通混凝土中的性能差异，取文献[15]中的试验数据进行对比，样本参数见表2。

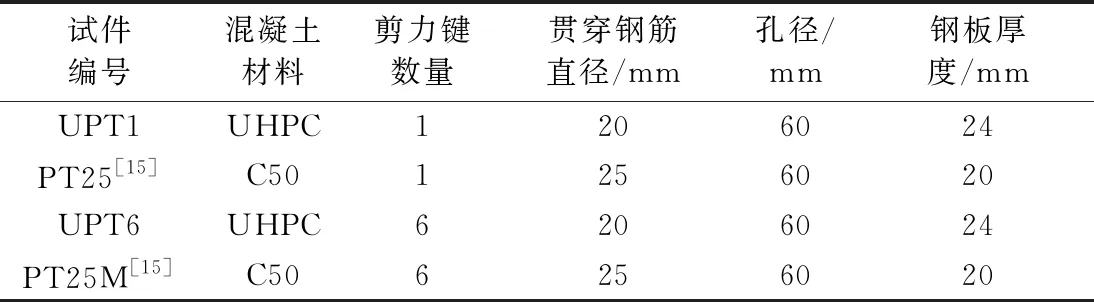
表2 推出试件参数表

关于PBL剪力键的设计承载力PRd，各研究学者有提出不同的计算方法[16-18]，但在适用性上有区别，文献[15]中提出一种既考虑PBL剪力键的变形又从宏观上考虑剪力键受力状态的方法，即将PBL剪力键的荷载-滑移曲线通过线性拟合的方式来确定正常使用阶段状态，当线性拟合的系数足够高时，则将该曲线段的最大荷载作为剪力键的设计承载力PRd。这种方法比较符合UHPC中PBL剪力键的实际工作状态，因此采取该方法拟合确定剪力键的设计承载力。拟合结果见图14，图14中的拟合系数均大于0.9。

图14 设计承载力线性拟合结果

本文中剪力键的抗剪刚度取为荷载-滑移曲线中正常使用阶段的割线斜率Ks为

Ks=PRd/δRd

( 1 )

式中：δRd为设计承载力对应的相对滑移量。

剪力键的延性系数Dc是其变形能力的体现，Dc计算式为

Dc=δu/δRd

( 2 )

式中：δu为剪力键破坏时的极限滑移量。

3.2 PBL剪力键的静力性能指标对比

各组试件的静力性能指标试验结果见表3，表3中数据均为同组试件的平均值。由表3可知，UPT试件的极限承载力、设计承载力、设计滑移量以及抗剪刚度都优于PT试件，而PT25的延性系数要优于UPT1。

表3 PBL剪力键的静力性能指标

下面对两类混凝土试件的主要力学性能指标进行对比分析。

3.2.1 设计承载力

PT25、PT25M试件的设计承载力分别为UPT1、UPT6试件的59%、76%，两者除混凝土材料不同以外，PT试件的贯穿钢筋直径更大，说明在正常使用阶段内，混凝土强度是影响PBL剪力键设计承载力的主要因素，UHPC可显著提高PBL剪力键的设计承载力。UPT6、PT25M试件的单键设计承载力分别为UPT1、PT25试件的44%、56%，说明在正常使用阶段，UHPC中剪力键之间受力的不均匀程度较普通混凝土中更高。

3.2.2 极限承载力

各组试件的平均单键极限承载力大小排序为：UPT1>PT25>UPT6>PT25M，UPT1试件的极限承载力为PT25的1.98倍，UPT6试件的极限承载力为PT25M的1.47倍，可见UHPC可显著提高PBL剪力键的极限承载力。UPT1试件的极限承载力为UPT6试件的2.25倍，而PT25的极限承载力为PT25M的1.67倍，说明UHPC中各剪力键受力更不均衡。

3.2.3 抗剪刚度

在正常使用阶段，孔内混凝土强度和贯穿钢筋直径共同决定了剪力键的抗剪能力。PT25、PT25M试件的抗剪刚度分别小于UPT1、UPT6试件，且PT25试件的抗剪刚度仅为UPT1试件的60.35%，可见UHPC能显著提高PBL剪力键的抗剪刚度。UPT6试件中贯穿钢筋截面面积仅占PT25M试件中的64%，但UPT6试件的抗剪刚度是PT25M试件的1.14倍，说明UHPC的高强特性可弥补贯穿钢筋直径较小所导致的剪力键抗剪刚度不足。

3.2.4 延性系数

剪力键延性系数是极限滑移量与设计滑移量的比值，主要体现其变形能力。由表3可知，各剪力键的设计滑移量相差不大，但极限滑移量相差较大。PBL剪力键塑性阶段的变形主要来源于：①混凝土榫被压碎后在贯穿钢筋挤压下发生的塑性流动;②贯穿钢筋的弯曲与剪切变形[4]。由于UHPC中钢纤维的桥接作用，在破坏时未发生塑性流动；一般来说贯穿钢筋直径越小越易弯曲变形，但由于UHPC对贯穿钢筋较强的支撑作用，使得贯穿钢筋破坏时以剪切变形为主。以上原因使得UPT1的极限滑移量远小于贯穿钢筋直径更大的PT25试件。对于群孔PBL剪力键，由于其滑移量取多个剪力键平均值，以此计算的延性系数不宜用于评估剪力键的延性。综合说来UHPC中PBL剪力键的延性有所降低。

4 既有承载力计算式的适用性

通过试验建立剪力键的结构参数与承载力之间的关系，可以使实际工程只根据剪力键的结构参数就能计算得到较精确的承载力，目前各国规范和一些研究学者均给出了PBL剪力键承载力的计算公式，见表4，参考各类公式计算得到承载力理论值与试验值的对比见表5。

表4 PBL剪力键的承载力计算公式

表5 PBL剪力键的承载力值对比 kN

对于UHPC中PBL剪力键的极限承载力，文献[17]、文献[18]以及文献[13]所得的承载力计算值均比试验值小，但文献[18]的计算结果相对试验值过于保守，文献[17]、文献[13]规范得到的计算值与试验值接近。对于设计承载力，文献[14]所得的承载力计算值比试验值高，文献[14]的计算结果比试验值小且较为接近，因此UHPC中的PBL剪力键承载力设计值可偏安全地按计算式PRd=[β1ξ(t/D)Acfc+β2Atrfy]/γv得到，其中，γv为安全系数，推荐取1.1。

目前各类公式以影响系数来表示贯穿钢筋和混凝土榫两者对剪力键承载能力的作用，相比普通混凝土，UHPC由于其优异的力学特性使得埋入其中的剪力键承载能力大大提高，此时孔内混凝土榫、贯穿钢筋对剪力键承载力的贡献发生改变，建议进行更多的试验研究并对相应公式的系数做出调整。同时，UHPC更高的弹性模量导致PBL剪力键群的受力分配更不均匀，对于集簇布置的PBL剪力键，其承载力折减系数尚待更深入研究。