人机共驾车辆路径跟踪集成控制策略

张新荣，许权宁，宫新乐，李学鋆，黄 晋

（1.长安大学 道路施工技术与装备教育部重点实验室，西安710064，中国；2.清华大学 车辆与运载学院，北京100084，中国；3.武汉理工大学 汽车工程学院，武汉430070，中国）

自动驾驶技术可以有效提高车辆安全，但由于技术难点多，高度自动驾驶短时间内无法实现。作为补充过渡阶段，人机共驾技术通过协调驾驶员与自动驾驶控制系统之间的关系，可以保证驾驶员的驾驶意图和驾驶感受，同时实现驾驶员与自动系统对车辆的协同控制[1]。

人机共驾车辆路径跟踪控制实际上是驾驶员与自动化系统之间的协同转向控制问题[2]。驾驶员和自动转向系统间的协同是影响驾驶员安全操作及人机冲突的重要难点[3-4]。K.Park 等[5]认为驾驶员长期积累负面情绪，如愤怒、焦虑、不信任会加剧人机冲突，控制器故障的可能性也会大大增加。T.A.Nguyen 等[6]利用模糊算法实现了基于驾驶员活动不确定性的共享转向控制。L.Saleh 等[7]提出了一种转向共享控制的方法，来处理驾驶员的不确定性行为。J.J.Rath 等[8]考虑了驾驶员的驾驶经验与风格，设计了基于模糊算法的共享控制器；同时研究了其他影响共享转向控制的因素，如控制器参数的变化、驾驶员活动的不确定性、干扰等。M.Hassanain 等[9]考虑了控制器参数变化、外界干扰等原因，设计了基于的人机共驾控制器。S.M.Petermeijer等[10]设计了基于线控转向系统的共享控制策略。

通过改善车辆稳定性可以显著减小交通事故发生的可能性[11]，因此众多学者对智能汽车稳定性控制做了深入研究，主要通过主动前轮转向系统[12]、集成控制系统[13]和差动制动系统[14]等来提高车辆行驶稳定性。P.Falcone 等[15]设计了基于模型预测控制的主动前轮转向系统控制器，通过约束车辆轮胎力在线性区域保证行驶稳定性。C.J.Gerdes 等[16]通过定义质心侧偏角约束、横摆角速度约束和道路安全约束，设计了自动驾驶车辆避障和稳定性集成控制器。JI Xuewu 等[17]采用博弈论解决了基于主动前轮转向系统和主动后轮转向系统的路径跟踪问题。商高高[23]等提出了一种基于稳态增益的主动转向系统可变传动比模型，提高了车辆的操纵便利性和行驶安全性。人机共驾车辆路径跟踪和稳定性集成控制已成为人机共驾研究的关键问题之一，如何在减小人机冲突和减小驾驶员操作负担的同时确保车辆路径跟踪能力和安全可靠性需要进一步研究。

本文针对串联式人机共驾车辆安全稳定行驶问题，提出一种集成控制策略，构建考虑车速和路面附着系数的主动前轮转向系统（active front steering system，AFS）变传动比曲线，兼顾车辆高速稳定性和低速灵活性，提升行驶安全性；设计基于模型预测控制（model predictive control，MPC）的共享控制器，实现人机共驾车辆高精度路径跟踪控制，且兼具一定的鲁棒性。该策略旨在提高前轮转向车辆人机协同控制的路径跟踪精度和横向稳定性。

1 框架描述

并联式和串联式人机共驾框架分别如图1 所示，并联式框架将控制器和驾驶员独立为2 个闭环，分别得出控制器前轮转角(θc)和驾驶员前轮转角(θd)，再通过权限分配系统对其进行合理的权重分配，以实现人机交互控制。并联式框架控制效果好，精度高，但是其人机驾驶权分配数学模型尚不明朗，同时很可能产生人机冲突的问题。串联式框架将驾驶员的θd作为控制器的输入，通过追踪目标路径和驾驶员前轮转角得出车辆前轮转角(θf)，以反馈补偿的形式实现了人机共驾[22]。其无需考虑人机冲突和驾驶权分配问题，控制效果良好且十分可靠。

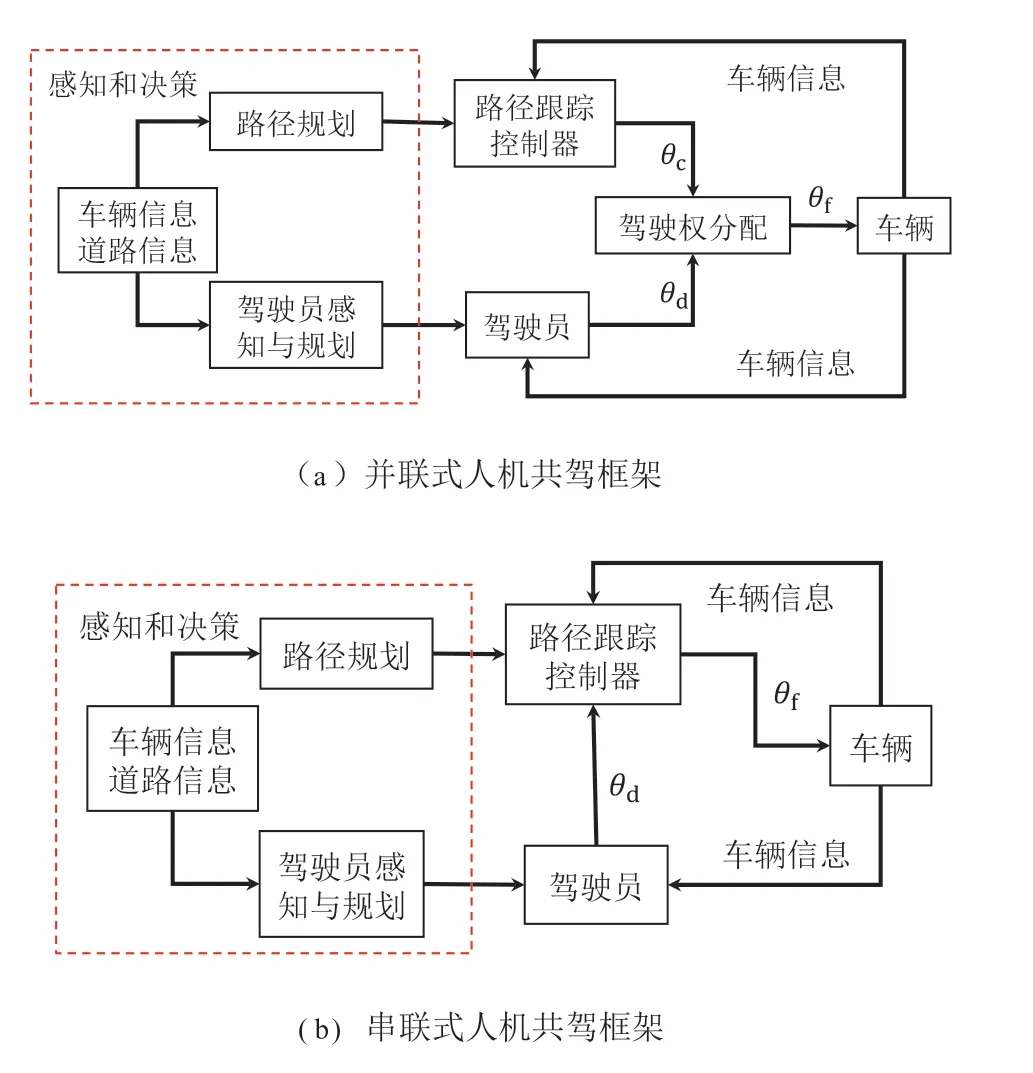
图1 人机共驾框架分类

本文基于串联式人机共驾框架，进一步集成主动前轮转向系统，构建了集成式人机共驾框架，如图2 所示。其中，Yd为目标路径；为驾驶员得出的横摆角速度；δMPC为控制器前轮转角；Δδ为前轮转角修正量。设计了MPC 控制器，其输入为期望路径和期望横摆角速度，期望横摆角速度由驾驶员基于期望路径得出，实现人机共驾车辆的路径跟踪控制。同时采用一种基于车速和路面附着系数的转向系统可变传动比曲线，通过主动前轮转向系统进一步提高了车辆在不同路况的转向稳定性。

图2 集成式人机共驾框架

2 AFS 变传动比曲线设计

传统转向系统传动比固定，导致转向操作时稳定性较差，不能严格保证汽车行驶的安全性、稳定性、轻便性。主动前轮转向是典型的助力转向，如图3 所示，其双排行星齿轮共用一个行星架进行动力传递，方向盘转角输入给前排太阳轮，经行星架传递到后排太阳轮，同时助力电机叠加转角经后排齿圈传递给行星轮，二者叠加后传递给后排太阳轮，最终通过齿轮齿条转向器传递给前轮。AFS 通过分析车速等信息判断车辆行驶状况，计算当前条件下适当的角传动比，通过助力电机实施相对应的叠加转角，最终实现变传动比转向。本节结合主动前轮转向系统，设计了基于路面附着条件和车速的可变传动比函数，以提高转向系统传动比的有效性，改善车辆的转向性能。

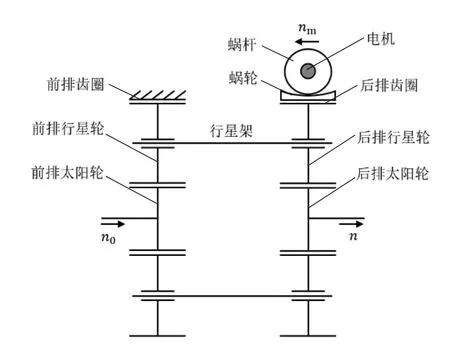
图3 双行星齿轮机构简图

n0、nm和n分别为输入轴转速、电机转速和输出轴转速。输出轴转角、电机转角和方向盘转角之间的关系如式(1)所示

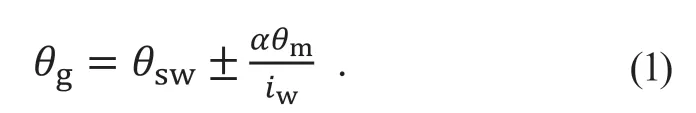
其中：θsw为方向盘转角；θm为电机转角；θg为输出轴转角；iw为齿圈与助力电机的传动比，α为主动前轮转向系统后排齿圈与太阳轮齿数之比。

齿轮齿条转向器传动比ig可表示为

其中，θf为前轮转角。联立式(1)和式(2)可得

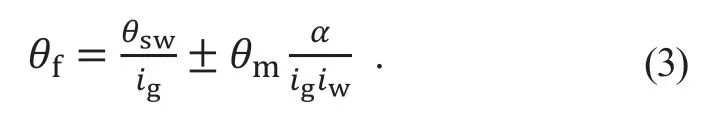
设助力电机叠加转角为 Δθf，则有

传统转向系统传动比固定，导致车辆理想横摆角速度增益Gsw数值随车速的增加呈非线性变化，需设计适当的变传动比i使Gsw保持恒定。变传动比曲线应考虑车辆高速稳定性和低速轻便性，防止传动比过大导致转向迟钝和传动比过小导致转向过于灵敏的问题，对传动比上下限进行约束。传动比i可表示为[18]：

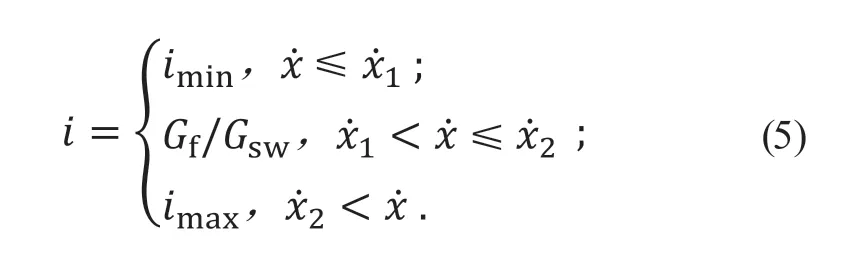
其中：imax和imin分别为传动比最大值和最小值；Gf为前轮转角到横摆角速度的增益；x·为车辆纵向速度；和为设定的车速节点。

理想前轮叠加转角为

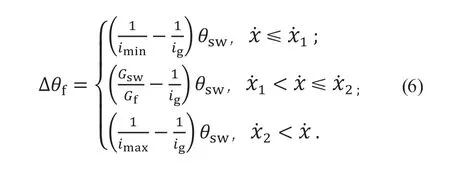
式(6)可满足转向系统传动比基本要求，但是和两点曲线曲率突变，同时没有考虑路面附着条件变化对车辆横摆角速度的影响，在恶劣附着条件下，较大的传动比可以避免过大的前轮转角。

可以得到如下三元非线性函数[18]

其中：μ为路面附着系数；k1和k2影响传动比最值；τ影响曲线走向；为边界速度值，本文取15。假设k1、k2和τ与μ均呈线性关系，进一步可得：

从图4 可以看出，不同路面附着系数的变传动曲线变化趋势基本保持一致，路面附着系数一定的情况下，传动比值与车速基本成正相关，车速一定的情况下，传动比与路面附着系数大致成负相关，与设计目标相符。

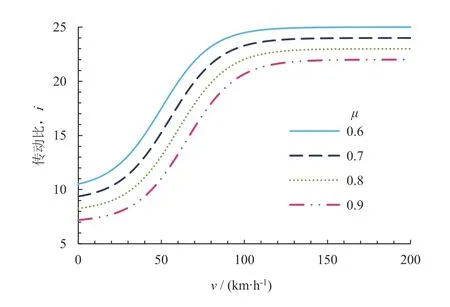
图4 不同路面附着系数的变传动比曲线

3 人机共驾车辆路径跟踪控制

3.1 人机共驾系统建模

3.1.1 三自由度车辆模型

为了进行MPC 控制器的设计，采用非线性3 自由度单轨车辆动力学模型[19]。为方便建模过程和减少控制算法计算量做出如下假设：1) 忽略路面坡度因素、车辆垂向运动及其与纵横运动的耦合效果；2) 忽略纵向和横向空气动力学；3) 车辆前轮转角保持较小，纵向速度保持不变，忽略前后轴载荷转移及横向载荷转移；4)忽略轮胎力的纵横向耦合关系，只考虑纯侧偏轮胎特性。图5 为3 自由度车辆动力学模型。

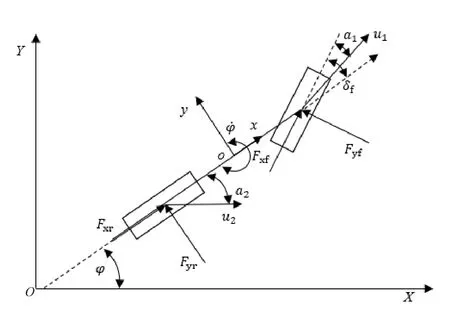
图5 3 自由度车辆动力学模型

根据示意图5 可以得到3 自由度车辆模型的动力学方程：

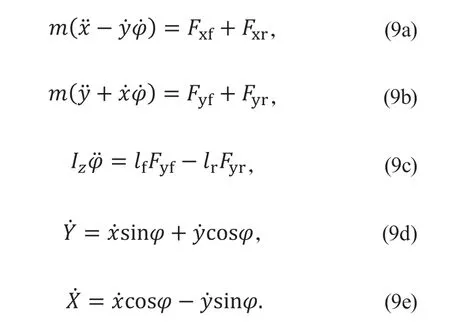
其中：m为整车质量；为车辆横摆角速度；Fxf，Fxr分别为前、后轴轮胎所受纵向合力，Fyf，Fyr分别为前、后轴轮胎所受侧向合力；lf，lr分别为车辆质心到前、后轴距离；x，y分别为车辆在自身坐标系的横向位移和纵向位移；X，Y分别为车辆在绝对坐标系的横向位移和纵向位移。

在满足假设条件下，轮胎纵向力和侧偏力可表示为:

其中：Clf，Clr分别为前、后轮纵向刚度；sf，sr分别为前、后轮滑移率；Ccf，Ccr分别为前、后轮侧偏刚度。

3.1.2 驾驶员模型

采用期望式驾驶员模型[20]，通过期望横摆角速度d与横摆角速度稳态增益Gf求得期望式前轮转角为d/Gf，体现了驾驶员稳定驾驶的操纵能力。

假设车辆在某段时间横摆角速度φ·维持恒定，因为汽车的纵向速度远大于横向速度，认为其车辆速度保持恒定，此时车辆做匀速圆周运动，前进的方向与即为目标路径的切线方向。图6 为恒定横摆角速度车辆轨迹，将车辆大小形状忽视，以其质心运动表现车辆运动。

图6 恒定角速度的车辆轨迹

其中：点G为当前时刻的车辆位置，点C为经过tp后的车辆位置，点P是目标路径上的预瞄点，Δf为实际路径与目标路径的预瞄偏差，点C的横向位置误差可表示为

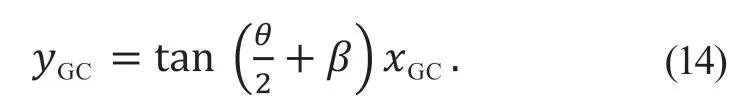
其中：θ为圆心角，β为质心侧偏角。

根据线性二自由度车辆动力学模型，稳态车辆横摆角速度保持恒定，横向速度保持恒定，此时横摆角速度稳态增益可表示为：

其中：δf为前轮转角，L为轴间距离，K为稳定性因子。

期望的横摆角速度可表示为

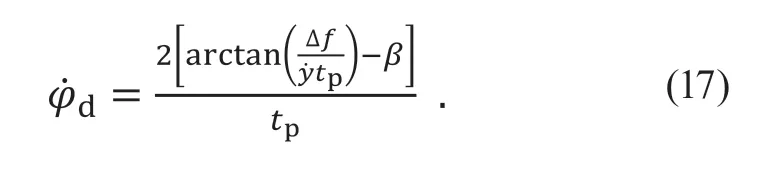
将式(17)代入式(15)中整理得期望式前轮转角为

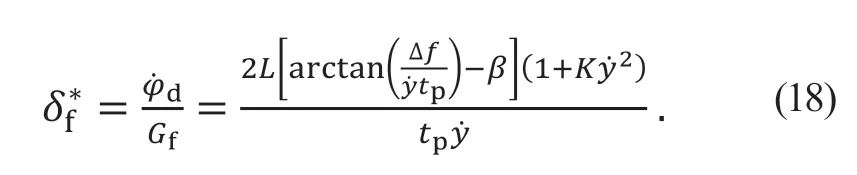
驾驶员转向模型可用图7 表示，其中td为神经反应滞后系数，th为动作反应滞后系数，tc为微分校正系数，不同的滞后系数表示驾驶员不同的驾驶状态。

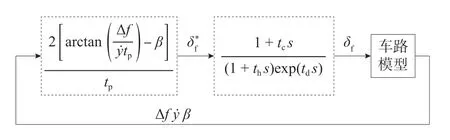
图7 期望式驾驶员方向控制模型

3.2 MPC 控制器设计

人机共驾路径跟踪控制器跟踪目标为期望路径及期望横摆角速度，其中横摆角速度(式17)为驾驶员在人机共驾系统中的输入，即驾驶员前轮转角(式18)与稳态增益(式15)的乘积，从而实现驾驶员与自动系统对车辆的共享控制。本文采用MPC 设计路径跟踪控制器，包括预测方程、代价函数和系统约束的设计。

3.2.1 模型线性化与离散化

设计MPC 控制器的需要对上述非线性连续系统进行线性化和离散化。采用针对状态轨迹的线性化方法,假设一段时间内对系统施加的控制量u0持续不变，得到期望状态轨迹，根据其与非线性模型实际状态量偏差进行控制器设计。将式(19)在某工作点[X0,u0]进行Taylor 展开，仅保留一阶项，得到线性时变方程为

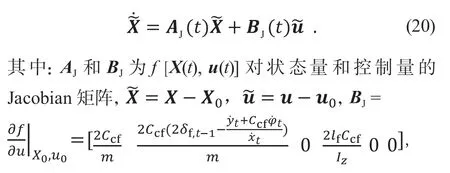
对式(20)采用一阶差商的方法进行离散化，采样时间为Ts，离散化后系统可表示为：

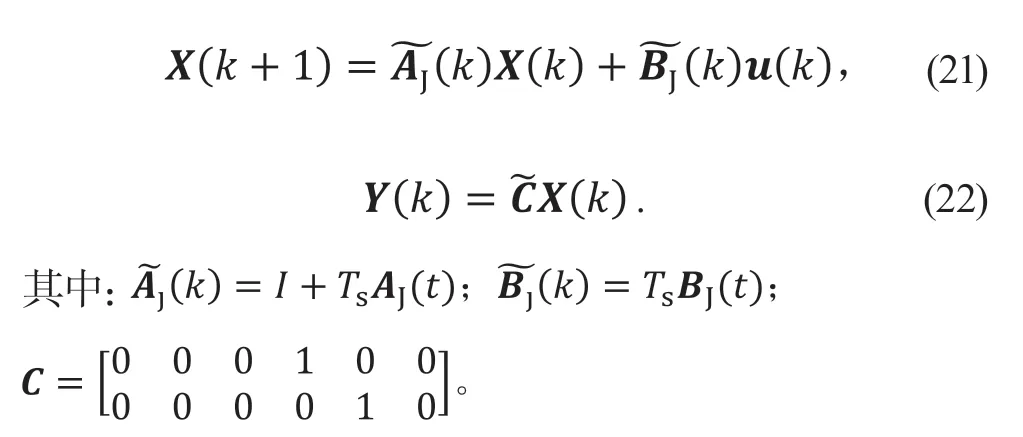
3.2.2 系统约束

在设计控制策略时，需要考虑转向系统执行器的饱和，设计转向约束如下：

其中：δf(k+i)为预测时域为k+i时的前轮转角，δf,sat为转向系统最大允许前轮转角，取25°。

通过限制两步控制动作之间的变化，保证了控制动作的平滑性。设计转向增量约束如下：

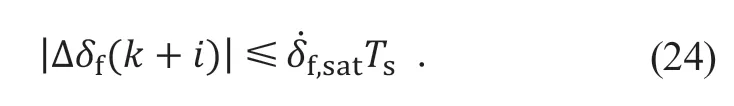
其中：f,sat为转向系统最大允许前轮转角变化量，取1.5 °[15]。

3.2.3 目标函数

为了处理路径跟踪问题，应使车辆实际路径与期望路径的偏差和车辆实际横摆角速度与期望横摆角速度的偏差尽可能的小，同时能够保证车辆路径跟踪能力得到很大的改善，因此优化目标函数可表示为：

其中：(t+i|t)表示在取样时刻t对取样时刻t+i的预测值，在符号“|”之前的t+i表示取样时刻t+i的预测状态，在“|”之后的t表示现在的取样时刻是t。表示车辆的横向位置误差eY和横摆角速度偏差表示输出量和相应的参考值。表示期望横摆角速度，表示跟踪的期望路径；；Q和R为状态量和输入量的加权矩阵。

为便于控制器设计，构造新的状态空间为[15]：

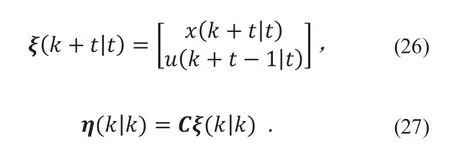
因此,系统输出量和系统状态量之间的关系为：

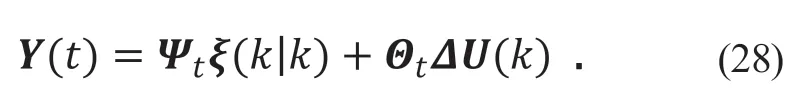
系统预测输出量为：

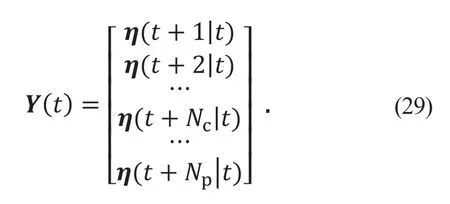
系统状态矩阵为：

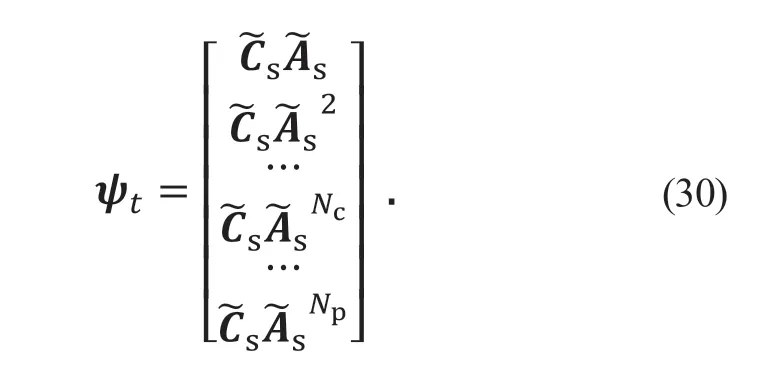
控制量增量矩阵为：

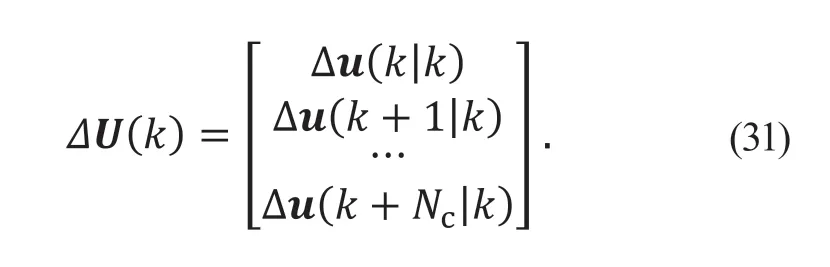
控制矩阵为：

在每个控制周期内，解出如下约束优化问题：

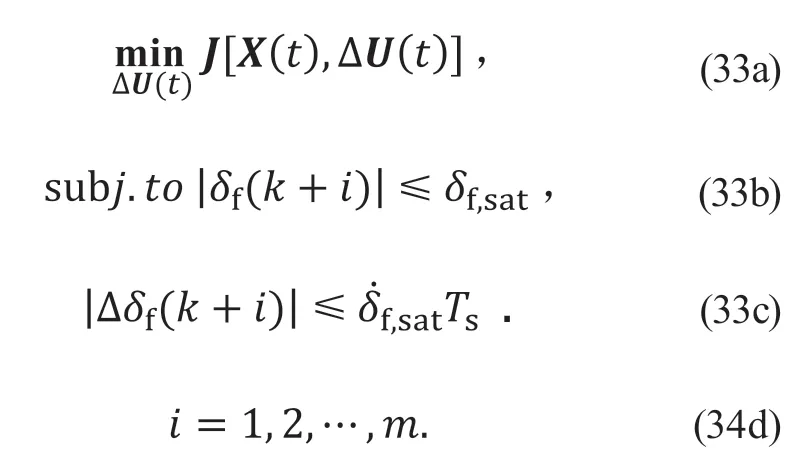
在每个控制周期内求得最优控制增量序列：

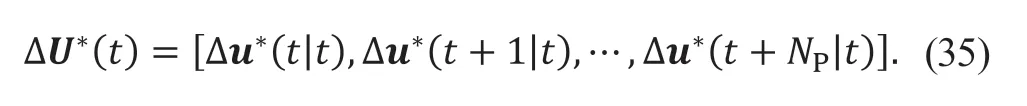
将该序列第一项作为当前时刻系统控制量增量，根据状态反馈控制律得到此时系统控制量为：

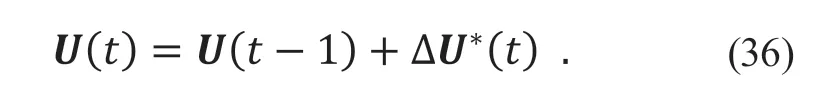
在每一个控制周期内，基于新的状态变量，重复解决上述优化问题。

4 仿真验证

为了验证所提出的集成控制策略的有效性，基于Carsim/Matlab 仿真平台搭建系统进行仿真并分析结果，采用有效集法(active set method)求解。采用的车辆参数见表1。

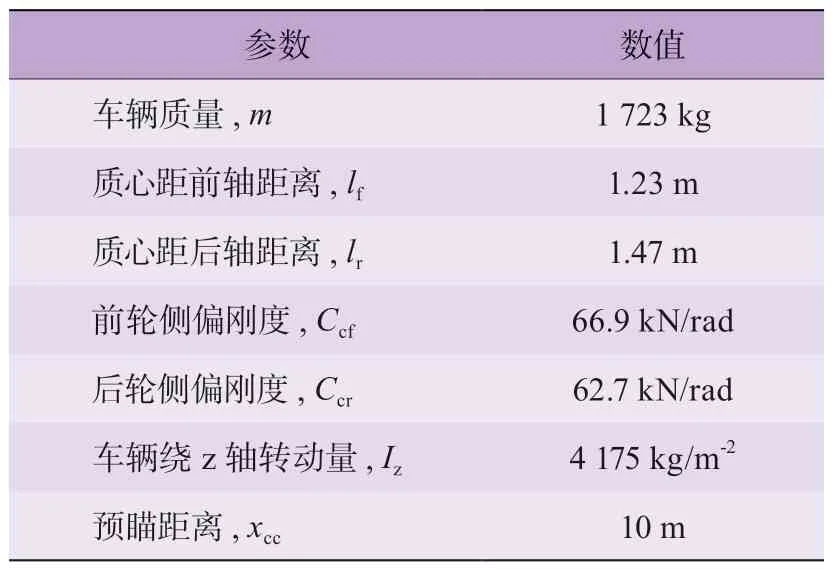
表1 车辆参数

本文只考虑人机共驾车辆的共享转向控制，因此假设在预测时域内车辆纵向速度保持恒定。设置两个基于Carsim B-Class 车辆模型的仿真工况。分别基于MPC 控制器与LQR 控制器设计人机共驾系统并加以对比，LQR 是车辆路径跟踪和稳定性控制中广泛使用的一种最优控制方法[21]。

控制器相关参数设置见表2：

表2 控制器参数

4.1 仿真工况1

仿真工况1 为车速72 km/h 的回转工况，用于模拟车辆在实际道路上连续转弯的情况，能够体现车辆横摆稳定性和路径跟踪性能。回转路径路面附着系数不是固定的，其具体变化情况如图8 所示，用于验证基于MPC 的人机共驾车辆在不同道路环境下的跟踪精度，同时验证变传动比(variable ratio curve，VSR)曲线对车辆稳定性的改善情况。可通过Kalman 滤波的方法对汽车状态参数估计，从而获得精确度较高的路面附着系数[24]。th=td=0.1，此时驾驶员驾驶状态良好。具体的分组为：基于变传动比曲线和MPC 控制器的人机共驾车辆、基于固定传动比(FSR，i=16)和MPC 控制器的人机共驾车辆、基于变传动比曲线和LQR 控制器的人机共驾车辆。

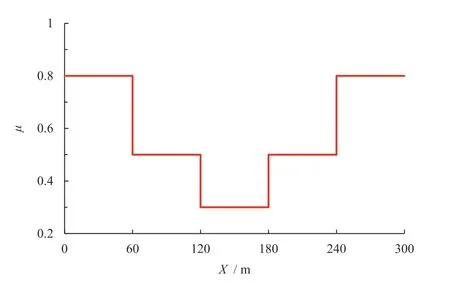
图8 工况1 路面附着系数

图9 为工况1仿真结果，表3 为各项指标的均方根。

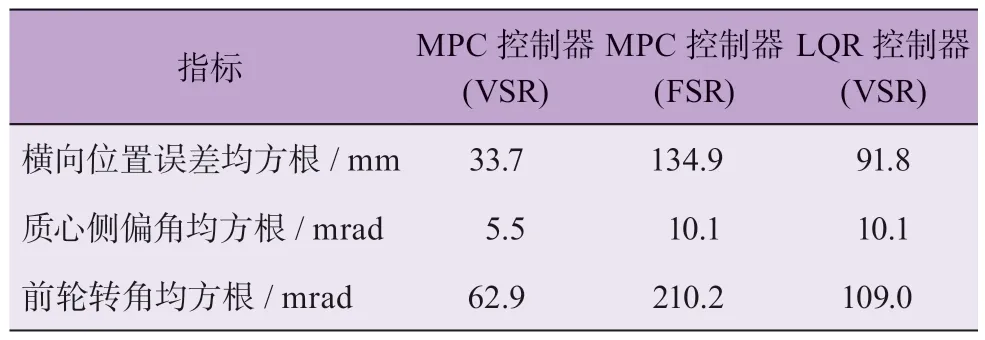
表3 工况1 仿真结果对比

如图9a 和图9b 所示，与固定传动比相比，可变传动比车辆可以在路面附着系数(μ)变化的情况下，均保持较高的路径跟踪精度，横向位置误差(eY)的均方根降低了75.01%；尤其是在低附路面，固定传动比车辆横向位置误差峰值高达546.8 mm，很可能产生失控和碰撞的事故，而可变传动比车辆横向位置误差峰值仅为114.9 mm。这是由于在低附路面通过可变传动比曲线(式7)，AFS 施加负的叠加转角以保证车辆的安全性与稳定性。

从图9c 和图9d 可以看出，相对于转向系统传动比固定的车辆，可变传动比车辆的质心侧偏角(β)更加稳定，其均方根分别下降了45.54%。在120～180 m 的低附路面，固定传动比车辆的质心侧偏角变化更为剧烈，这意味着车辆失控的风险大大增加。在均为变传动比的情况下，MPC 控制器则比LQR 控制器更有优势。

如图9 所示，在高附路前轮转角面，2 种控制器均能达到正常行驶的要求；然而在低附路面，MPC 控制器在路径跟踪精度和车辆稳定性能方面更加优越。基于MPC 的人机共驾车辆横向位置误差均方根为33.7 mm，相比LQR 控制器降低了63.29%；同时质心侧偏角和横摆角速度2 个稳定性指标也分别降低了45.54%和16.36%，保证了车辆路径跟踪过程中的稳定性。

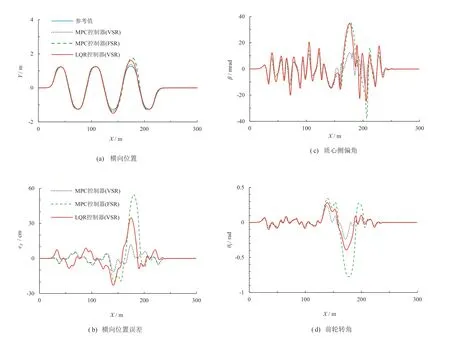
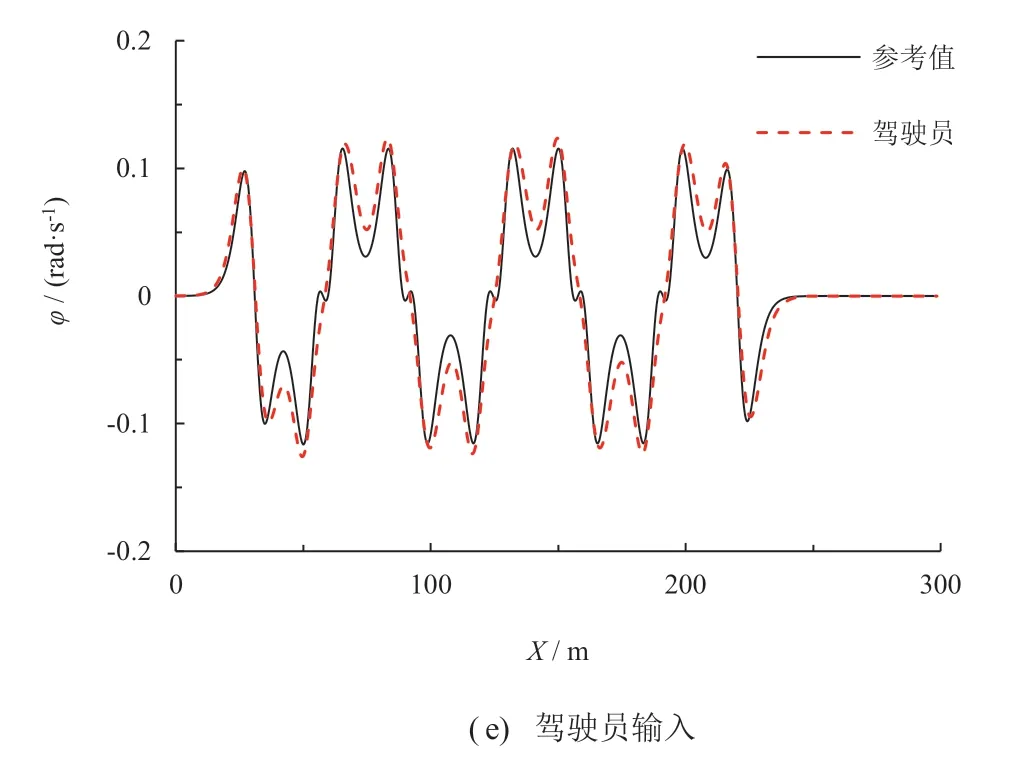
图9 工况1 仿真结果

如图9d 所示，MPC 控制器使车辆前轮转角收敛更为平缓，体现了良好的乘坐舒适性和更小的驾驶员操作压力。图9e为驾驶员基于路面信息得出的横摆角速度(φ)，可以看出当驾驶员驾驶状态良好，其对控制系统的输入与参考值十分接近，可以同时确保路径跟踪精度与良好的驾驶体验。充分说明MPC 控制器具有一定的鲁棒性，路面情况的改变对其路径跟踪效果影响相对较小，确保人机共驾车辆在路径跟踪过程中具有良好的稳定性。

4.2 仿真工况2

仿真工况2 为72 km/h 的双移线工况，用于模拟车辆紧急避障或超车的情况。路面附着系数μ=0.8。，更大的神经反应系数和动作反应滞后系数意味着驾驶员更差的驾驶状态，即无法对道路情况做出快速合理反应，极大影响路径跟踪效果。此工况主要用于验证所提人机共驾框架及集成控制策略的有效性，分为：基于MPC 控制器的人机共驾车辆、基于LQR 控制器的人机共驾车辆和驾驶员单独驾驶的车辆。三者转向系统均具有变传动比曲线（式7)。

图10 为工况2 仿真结果，表4 为各项指标的均方根。如图10a 和图10b所示，由于驾驶员较差的驾驶状态，驾驶员单独驾驶的车辆在50、90 m 的转弯处产生了较大的车道偏移程度，同时其质心侧偏角和前轮转角波动更为激烈，表示车辆无法确保稳定的路径跟踪。如图10e 所示，驾驶员得出的横摆角速度与参考值相差较大，其较差的驾驶状态造成了极大的驾驶负担，无法确保车辆的安全行驶，此时控制器对驾驶员输入进行修正和补偿以提高路径跟踪精度，相当于控制器具有更高的驾驶权重。本文提出的串联式人机共驾框架很好地改善了这一问题，基于LQR 的人机共驾车辆提高了路径跟踪精度，其横向位置误差均方根下降了17.11%。同时车辆稳定性能也有所提高，质心侧偏角在转弯处振荡频率和幅度更小，其均方根分别降低了1.63%。前轮转角更为平滑，其均方根下降了38.24%，改善了车辆的安全性和稳定性。但受限于LQR 控制器的控制性能，人机共驾车辆路径跟踪精度和车辆稳定性改善情况相对有限，MPC控制器则进一步提高了车辆性能。

表4 工况2 仿真结果对比

从图10 可知，基于MPC 的人机共驾车辆几乎没有被驾驶员的不良驾驶状态所影响，3 项驾驶指标分别降低了56.97%、4.92%和51.20%，尤其是车辆的路径跟踪精度得到了很大的改善，同时保证了车辆稳定性，失控的风险进一步降低。以上结果说明所提出的MPC 控制器可以处理因驾驶员较差的驾驶状态对人机共驾车辆造成的影响。

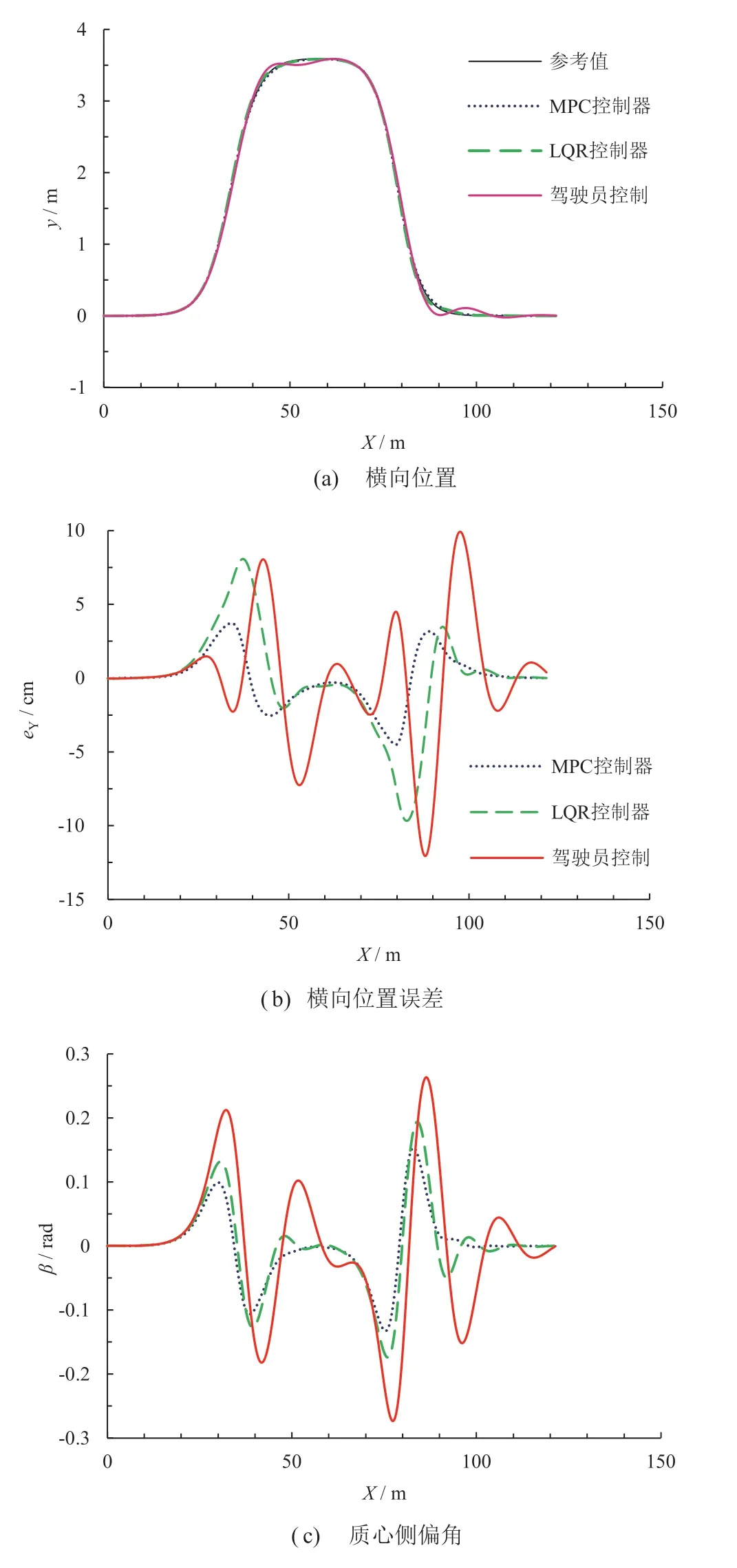
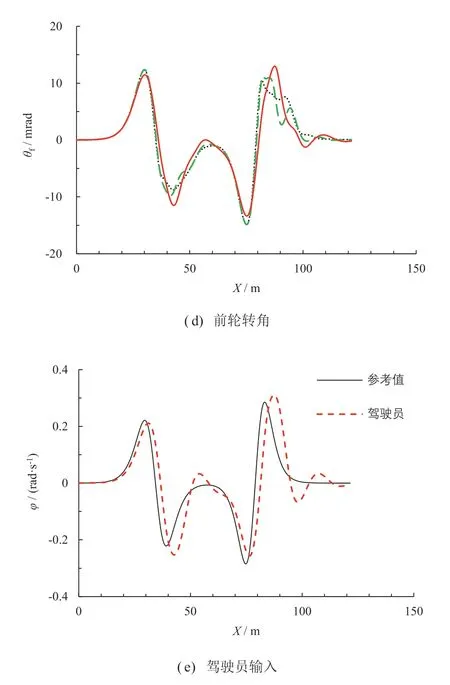
图10 工况2 仿真结果

5 结论

本文针对人机共驾车辆路径跟踪和稳定性问题，提出一种基于主动前轮转向系统和模型预测控制的集成控制策略，即基于MPC 设计了人机共驾车辆路径跟踪控制器，并采用主动前轮转向保证了跟踪过程中的稳定性。针对横摆稳定性控制，设计了基于车速和路面附着条件的AFS 可变传动比函数，用于改善车辆的转向性能，有效提高了人机共驾车辆行驶过程中的安全性与稳定性；针对路径跟踪控制，基于MPC 设计了人机共驾车辆路径跟踪控制器，在驾驶员状态波动的情况下可以实现准确快速的跟踪效果。研究结果表明，所提出的集成控制策略可以提高人机共驾车辆的路径跟踪精度和横向稳定性，在驾驶员驾驶状态不良的情况下可以保证良好的控制效果。

后续将进一步扩展本文所提出的路径跟踪及稳定性控制框架，研究考虑时变车速下的纵向控制问题并于现有框架结合，以期实现车辆在不同车速下的精准稳定路径跟踪，提高算法的适用性。