基于改进无偏灰色马尔科夫动态模型的山东海上辖区险情事故量预测1

王士鹏，周兆欣，于皓琛，马续仕，秦 圻，韩 洋

1.山东交通学院航运学院，2.交通运输部北海救助局

0 引 言

随着全球新冠疫情的冲击和贸易一体化网络的形成，我国对于海上运输物资的需求量不断增大，海上船舶交通流和物流贸易量稳步增长。因此，如何确保我国海上交通安全，避免险情事故的发生，更是迫在眉睫。海上险情事故是指对水上人命安全、水域环境构成威胁，需立即采取措施控制、减轻和消除的各种事件，不同于海上事故的是，险情事故包括并包含一切海上船舶、设施等引起的事故，如碰撞、搁浅、火灾、沉没等，一般指事故发生时的初始阶段[1-2]。然而，由于险情发生时受季节、环境等多方面综合因素的影响，具有时间序列多变性和模糊性。因此，如何对险情事故量进行精准预测，仍是国内外学者研究的热点问题。

目前，学者们对水上交通险情事故预测的研究主要集中在传统机器学习部分，杜柏松等[3]提出了马尔科夫预测理论修正和粒子群算法优化的改进SCGM（1，1）C预测模型，并对2005—2019年海上交通事故进行了预测；陈昌源等[4]提出了一种改进的灰色预测模型，以2004—2014年海上交通事故数为基础，进行传统灰色模型预测，并与二阶弱化模型预测和改进模型预测的结果进行了对比；范中洲等[5]利用灰色BP神经网络对全国海上交通事故数进行了预测：李铃铃等[6]通过建立灰色神经网路对某水域的水上交通事故量进行了预测；虞盈等[7]基于灰色马尔可夫预测模型对福建辖区内2000—2015年船舶交通事故进行统计预测。基于此，灰色预测、神经网络预测和传统灰色马尔可夫链预测等方法已广泛应用于海上事故量预测领域中。但传统灰色马尔科夫预测模型存在计算过程复杂程度高和不适宜在系统中做长期预测的问题。因此，需构建一种预测精度和计算效率进一步提高的海上险情事故量预测方法。

本文提出一种改进无偏灰色GM（1，1）和马尔科夫链修正预测理论相结合的改进无偏灰色马尔科夫预测动态模型方法，应用到海上险情事故量预测领域，目前这一领域仍属空白。以山东海域辖区内2010至2021年的海上险情统计事故量为样本数据，与传统GM（1，1）、无偏灰色GM（1，1）和传统灰色马尔科夫模型的预测结果进行了对比分析，以期对传统预测方法下的预测模型做出改进，减小计算求解时的冗杂性，提高预测精度。对未来山东海上辖区内的水上交通安全提供一定的理论指导和数据参考。

1 灰色马尔科夫预测模型算法改进

1.1 传统GM（1，1）算法模型

灰色GM（1，1）算法预测模型是一种针对系统内分散时间轴下的离散数据，被看作一组连续变化的序列，通过累加、累减、弱化未知因素、强化已知因素、构建连续微分方程的数学方式确定参数，并做出系统预测的传统预测方法[8]，其通常建模步骤如下，首先设原始数列集合为：

式中，k表示第n年的海上险情事故量。

其次，对X（0）累加弱化时间序列波动性，为新生成一次累加序列：

生成X（1）的邻均值数列Z（1）为：

再次，构建灰色理论下的海上险情事故量预测的一阶一元微分方程：

式中，a、u分别表示为发展系数和灰色作用量。

将发展系数a和灰色作用量u代入可得预测方程为：

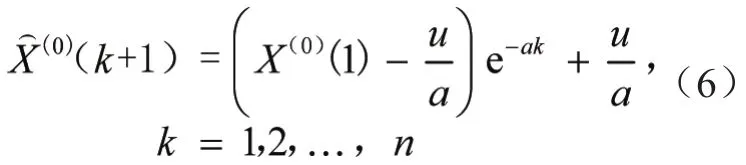
将上式结果通过累减还原可得海上险情事故量预测值为：

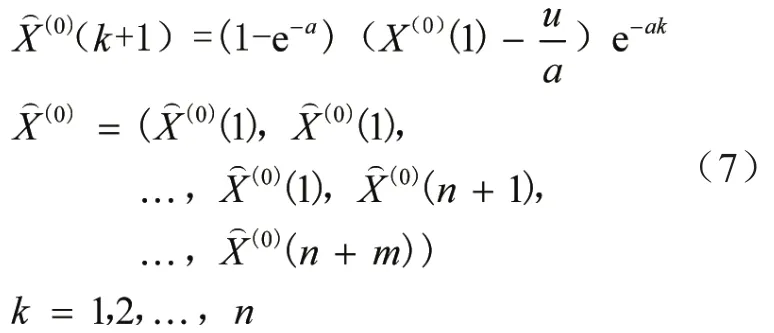
最后，检验模型预测精度，精度检验方法通常有：残差检验法、关联度检验法、均方差比值检验、小概率误差检验和小误差概率检验法[9]。本文选择均方差比检验（C）和小误差概率检验法（P），预测精度等级对照表如下表1所示。

表1 灰色预测精度等级对照表

总之，传统GM（1，1）算法模型不依赖于庞大的数据量，运算过程也相对简单。但对于长期的数据预测，其弊端在于对全局的发展信息掌握较为贫乏，只适用于中短期预测。同时，其作为一种存在参数偏差的指数预测模型，本身存在着故有偏差的问题，因此预测精度表现一般。

1.2 无偏GM（1，1）算法模型

首次对传统GM（1，1）提出无偏化改进的是我国学者吉培荣。该方法消除了传统GM（1，1）的参数偏差问题，简化计算步骤和提高预测精度[10]，一般计算步骤如下：

（1）在GM（1，1）的基础上求得参数a和u的值，并引入无偏灰色预测理论中的无偏参数b和M，如下所示：

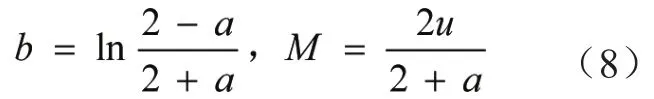
（2）根据上式计算结果，推导得出经无偏改进后的GM（1，1）预测模型：

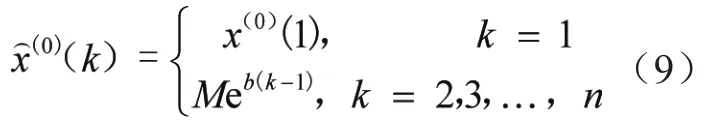
与传统GM（1，1）相比，无偏GM（1，1）消除了传统模型下所存在的故有参数偏差等问题，但对于离散、波动、随机大的事件数据上预测精度略显不足。

1.3 动态改进

GM（1，1）在做系统数据预测时，常常会因为数据序列波动大的问题导致预测精度快速降低。因此，引入动态建模思想对无偏GM（1，1）进行改进，对预测过程中的数据动态迭代，提高了预测精度。

1.4 改进无偏灰色马尔科夫模型

为了在无偏灰色GM（1，1）预测结果的基础上进一步提高预测精度，改进无偏灰色马尔科夫模型同灰色马尔科夫预测模型一样的计算流程，均在GM（1，1）结果的基础上计算残差e（k）和相对误差Q：

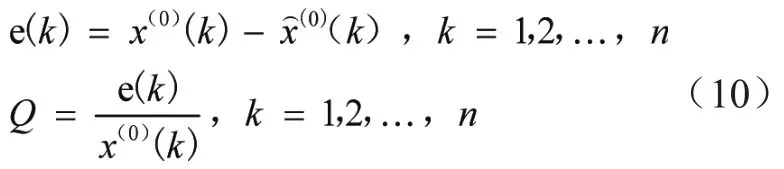
随后与马尔科夫链相结合的方式修正预测结果，通过残差序列值的相对误差分布情况，设置i个马尔科夫状态区间Ei[12]：

并建立根据标准划分不同的状态转移矩阵，记为Pij：

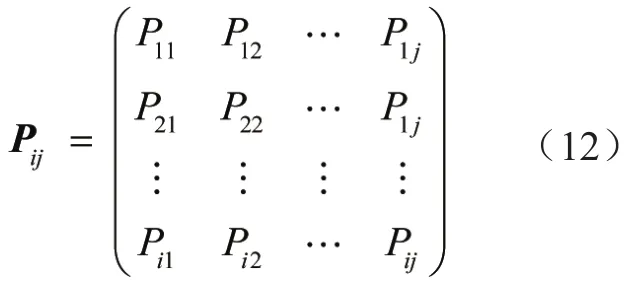
通过比较各状态概率的大小，得灰色马尔科夫预测模型公式[13]：

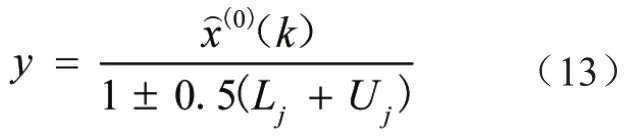
式中，对于±值的选择，通常在预测状态为“高估”时取正，“低估”时取负。

2 山东海上险情事故量预测

文中涉及的险情事故数统计数据来自于山东海事局官网数据发布的安全形势分析专栏中2010到2021年的海上险情事故统计量，见图1所示。采用改进无偏灰色马尔科夫动态预测模型进行预测分析，与传统GM（1，1）、无偏灰色GM（1，1）和传统灰色马尔科夫的预测结果进行了对比。

图1 山东辖区海上险情事故统计量

2.1 传统GM（1，1）与无偏GM（1，1）算法预测

将2010至2021年山东辖区海上险情事故量数据带入到原始数列X（0）为：X（0）=[215，150，160，154，125，94，132，108，104，84，77，96]。经公式（1）～（7）推导，利用Matlab2021b编程求解可得参数a和u分别为a=0.035 8和u=14.173 0，并代入公式得：

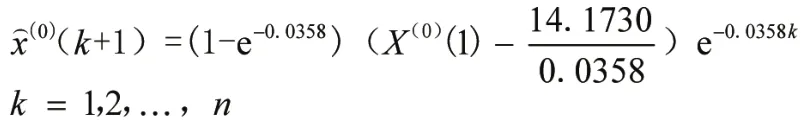
通过方差比检验（C）和后验差检验法（P）可知，C≈0.113 6，P≈0.916 7。预测精度对照表1可知为“合格”，预测精度仍不理想。

为进一步提高模型预测精度，采用无偏GM（1，1）进行了改进计算，计算主要步骤为[13]：

首先，将原始序列X（0）中前5个数据组成新原始序列X’（0）为：

X’(0)=[215，150，160，154，125]

其次，将新原始序列通过公式（8）～（9），可得参数a和u分别为a=0.041 0和u=11.637 9，代入无偏GM（1，1）预测模型公式得：

同时，根据无偏GM（1，1）动态建模下的预测数据迭代思想，在获得第6个预测值及2015年的险情事故量的基础上，将新原始序列X’（0）中第一个数据删除，同时将2015年的预测险情事故量加入到新序列中，依次重复上述步骤得到无偏GM（1，1）动态建模下的预测数据，并求得C≈0.071 2，P=1。预测精度对照表1可知为“好”，相比较于传统GM（1，1）的平均相对误差预测精度提高了2.16%，通过公式（10）计算传统GM（1，1）和无偏GM（1，1）预测模型的预测值、残差值、相对误差等部分数据，见表2所示。

表2 传统GM（1，1）和无偏GM（1，1）模型预测值

2.2 马尔科夫修正预测

对传统GM（1，1）和无偏GM（1，1）预测模型分别进行马尔科夫链修正预测，以无偏GM（1，1）预测模型为例，经公式（11）～（13），计算得出的残差值和相对误差值划分动态预测状态为E1、E2、E3和E4，见表3所示。

表3 无偏GM（1，1）预测模型状态划分

从而建立状态转移概率矩阵P，可同时求得多步状态转移矩阵，矩阵P为：

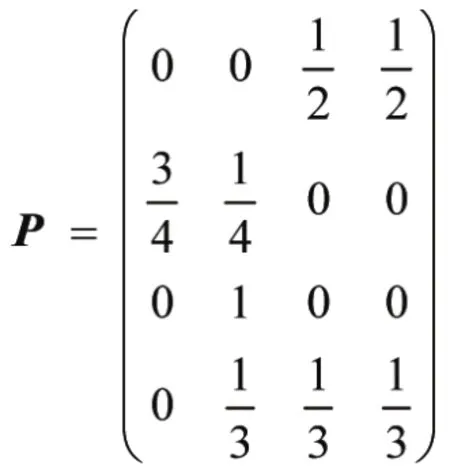
进而对无偏GM（1，1）下的动态预测值进行马尔科夫链修正，即可得改进无偏灰色马尔科夫动态预测模型下的预测值。预测数据结果对比见下表4所示。

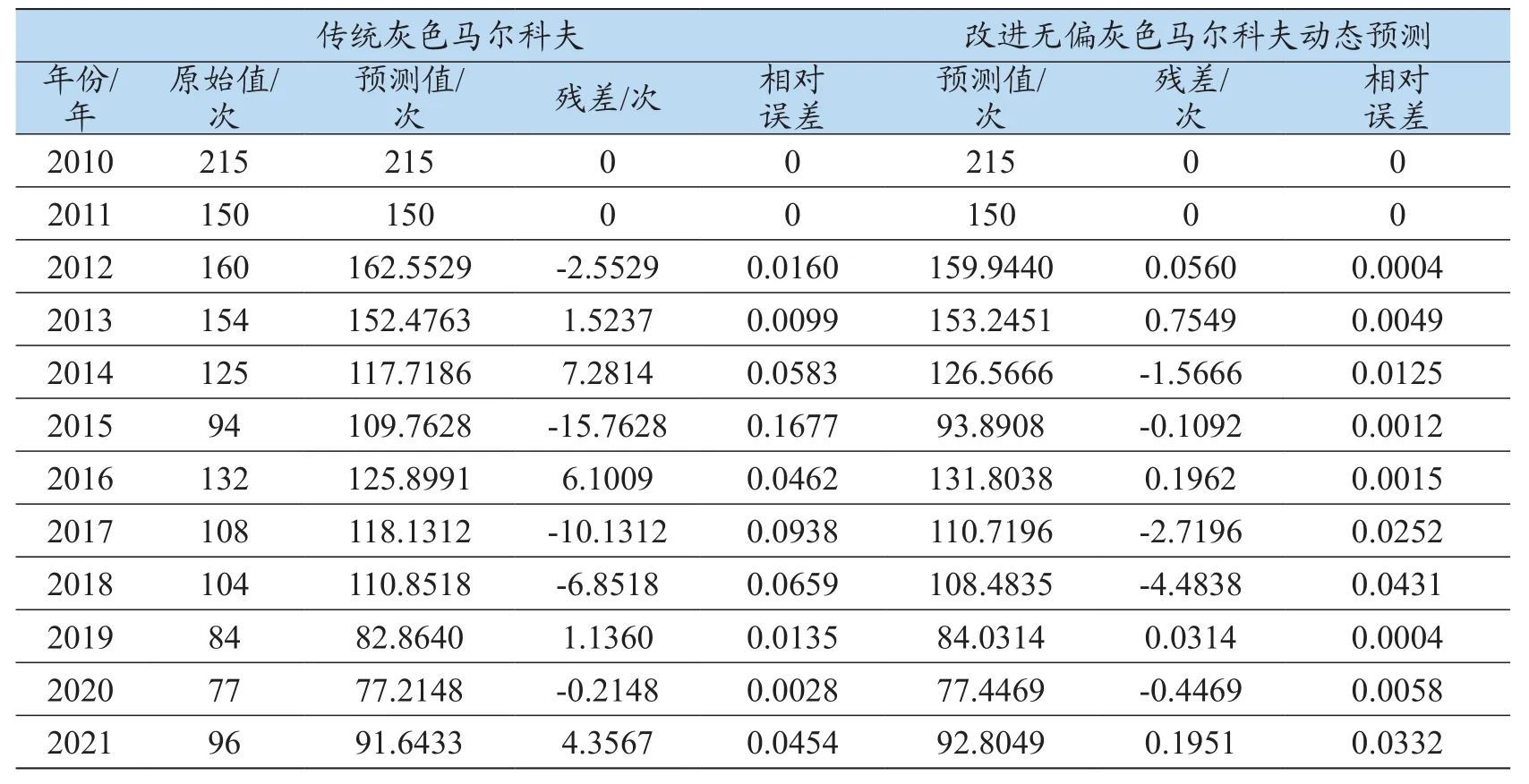
表4 传统灰色马尔科夫和改进无偏灰色马尔科夫动态预测效果对比

综上所述，分别求出传统灰色马尔科夫和改进无偏灰色马尔科夫动态预测的方差比C为C1≈0.028 7和C2≈0.021 6，P1=P2=1。改进无偏灰色马尔科夫动态预测相对于传统GM（1，1）、无偏GM（1，1）、传统灰色马尔可夫模型的平均相对误差降低了分别约为7.351 7%、6.341 7%和3.260 8%。同时绘制了四种模型的预测效果对比如图2所示，从图中可以看出改进无偏灰色马尔科夫预测模型的预测精度明显要高于传统预测模型。

从图2中可以看出改进无偏灰色马尔科夫预测的曲线与初始值曲线更契合，且相较其它模型的预测结果更加精确，验证了此预测方法的准确性。

图2 传统预测模型对比分析图

2.3 三大辖区海上险情事故量修正预测

为针对山东海上辖区安全形势做进一步数据分析与评估，确定海上安全防御及监控重点为何区域。根据险情事故量统计结果和参考北海救助局的日常值班和机动待命点及救助力量部署表，将山东海上搜救重心辖区划分为三大辖区，分别为以烟台辖区、威海辖区、石岛辖区和荣成辖区为主的鲁东辖区，以滨州辖区、潍坊辖区、东营辖区和大沽口外海辖区为主的鲁北辖区和以青岛辖区、日照辖区、海阳辖区和秦皇岛外海辖区为主的鲁南辖区，如图3所示：根据三大辖区的划分，分别对各辖区采用四种预测模型进行预测结果对比。鲁西、鲁东和鲁南辖区的海上险情事故量输入分别为：X（0）=[27，22，19，12，8，10，22，18，15，12，6，6]，X（0）=[140，89，108，76，72，52，60，49，51，41，39，43]，X（0）=[48，39，33，66，45，32，50，108，38，31，32，47]。

图3 山东省海上辖区划分图

重复上述推导过程，以期窥测、分析到更多数据和结论。预测结果见图4所示。

图4 鲁西、鲁东和鲁南辖区模型对比预测图

从图中分析可知：（1）改进无偏灰色马尔科夫预测动态模型相比于其它传统预测模型与原始数据契合度更高，具有较强的拟合性和高精度性。（2）鲁东辖区及以烟台和威海为主的海域海上险情事故的发生频率要远高于鲁西和鲁南辖区，究其原因是此辖区地处我国南北水上交通咽喉之地，成山头水道、长山水道和渤海海峡交界处的水上交通流密度大，来往船只船型复杂，渔商船矛盾较为突出。易于发生水上险情事故，应作为重点防御对象和预防重点海域。（3）在三大辖区险情事故预测趋势对比中，鲁东和鲁西辖区均呈现未来海上险情事故量稳中降低的趋势，反观鲁南辖区呈现明显的上升趋势，分析其地理位置可知，此处地处黄海海域，有丰富的水底鱼类资源，是我国四大渔场之一。因此此地渔船众多，且渔船由于其在人员管理、船型、业务素质等方面均与受过正规培训的海船船员不同，渔商船矛盾尖锐，易致海上险情事故的发生。因此，需要有关公司和渔港监督局等部门加强公司管理、提高船员职业素质、加强监察巡视等。

3 结 语

本文创新性地提出了一种改进无偏灰色GM（1，1）和马尔科夫链修正预测理论相结合的改进无偏灰色马尔科夫动态模型预测方法，应用于海上险情事故量预测，得到以下结论：

（1）通过对以山东海域辖区内2010至2021年的海上险情事故统计量为样本数据，以年为单位作为原始序列，采用改进无偏灰色马尔科夫预测模型与传统GM（1，1）、无偏GM（1，1）、传统灰色马尔可夫模型预测结果对比，平均相对误差预测精度分别提高了7.351 7%、6.341 7%和3.260 8%，验证了此预测模型的有效性，为山东省有关海上监管、水上交通安全管理及搜救部门提供了一定的理论和数据参考。

（2）将山东海上辖区分为以烟台辖区、威海辖区、石岛辖区和荣成辖区为主的鲁东辖区，以滨州辖区、潍坊辖区、东营辖区和大沽口外海辖区为主的鲁北辖区和以青岛辖区、日照辖区、海阳辖区和秦皇岛外海辖区为主的鲁南辖区，通过以上四种预测模型分别对各辖区的险情事故量进行了预测和趋势分析，预测结果同样验证了此方法的有效性，并针对结果提出应根据各自地理环境特点，具有针对性地把鲁南辖区和鲁东辖区的成山头水道、石岛水道和青岛及日照的黄海海域列为安全监管防御重点区域。

（3）改进无偏灰色马尔科夫动态模型预测结果（见图4），预测拟合曲线在2016年之后开始有了不同程度的误差偏移，还存在着参数误差的问题，需进一步进行残差修正。因此，未来将不断寻求相关算法对残差进行优化，期望进一步提高预测精度。