微裂纹群对主裂纹尖端损伤行为的影响*

李 煦， 苏 睿， 张 欢， 翁倩茹， 江晓禹

（1. 成都工业学院 智能制造学院，成都 610036；2. 西南交通大学 力学与航空航天学院，成都 610036）

引 言

在真实材料中，宏观裂纹尖端附近往往存在大量的微裂纹，它们不仅会在材料服役过程中产生，还可能在材料的制备过程中产生.图1 展示了U71Mn 钢在三点弯曲的恒定振幅疲劳载荷作用下的扫描电子显微镜下的观察结果[1]，即在宏观裂纹前方观察到一簇任意分布的微裂纹，微裂纹用红色箭头标注，微裂纹与主裂纹即将交汇处用红色圆圈标注.其中，试样为矩形板（120 mm × 15 mm × 1 mm），含有边缘裂纹.边缘裂纹位于试样中部，初始长度为2.846 mm.加载频率为1 Hz，最大负载和最小负载分别为1 kN 和0.1 kN.

图1 主裂纹尖端附近存在多条微裂纹Fig. 1 Several micro cracks were observed near the macro-crack tip

一般情况下，微裂纹与主裂纹或者微裂纹与微裂纹之间的相互作用效应会使得裂纹尖端的应力场不同于单条裂纹在同样外载荷作用下的应力场.因此，如何有效地了解裂纹影响材料失效破坏的机理，针对微裂纹与主裂纹的相互作用以及微裂纹对主裂纹扩展行为的影响开展高效且精确的理论研究工作是人们长期以来关注的重点问题.Gong 等[2-4]通过Muskhelishvili 复变函数法和应力叠加法研究了弹性平面内任意分布的微裂纹或微孔洞对主裂纹的影响.Petrova 等[5-7]通过小参数法研究了材料中多个微裂纹对主裂纹扩展的影响.Li 等[1,8]通过分布位错法研究了在单轴拉伸条件下主裂纹与微裂纹的相互影响.夏晓舟等[9]利用平均化法和叠加原理研究了裂纹间的相互作用机理.李亚等[10]利用应力强度因子的裂纹线法研究了局部均布荷载下Ⅰ型裂纹有限宽板应力强度因子.此外，研究者们[11-13]还利用有限元法研究了多个微裂纹与主裂纹的相互作用.但以上研究工作大多是针对主裂纹尖端存在少量微裂纹的情况，并且只考虑了微裂纹对主裂纹的影响.事实上，当主裂纹尖端存在大量微裂纹时，微裂纹之间的相互影响变得很重要.如果忽略微裂纹之间的相互影响，可能会对计算结果造成误差，影响下一步的研究.

另外，从损伤力学的角度出发，研究者们提出了两个重要的理论研究方法，即连续损伤力学方法和细观力学方法，但是对于微裂纹密度较大的情形，目前还是难以建立既符合材料损伤、破坏的力学机理，又便于实际应用的模型，只能通过一些近似简化、数值计算、实验测定得出近似解答[14-16].

综上所述，为了更好地研究平面多裂纹问题，既应该考虑微裂纹间的相互影响，还应该考虑微裂纹的数量、长度和分布形式等对主裂纹尖端的影响.在宏观平面弹性理论和断裂力学中，Muskhelishvili 复变函数法[17]是一种有效求解多连通区域或复杂几何形状等裂纹问题的方法，其主要求解思路是找到满足问题边界条件的复应力解析函数，利用保角变换法将z平面上复杂的裂纹问题通过转化为映射平面上相对简单的问题，得到平面内任意一点的应力分量、应变分量、位移分量等，最后得到满足裂纹面边界条件的问题的解析解，进而求得应力强度因子.

在前期的基础上[17-18]，本文将运用Muskhelishvili 复变函数法求解无限大平面内含一个主裂纹和多个任意分布微裂纹问题的理论解，进一步研究了单轴拉伸条件下主裂纹和微裂纹尖端的损伤参量D，分析了不同的损伤区形式对裂纹尖端损伤的影响.

1 Muskhelishvili 复变函数法和逐步递推法

1.1 理论方法

以图2 所示的问题为例，在无限大平面内含一条主裂纹和k(k=1, 2, ···,j, ···,n)条任意分布的微裂纹，无限远处有均匀拉伸载荷σ∞.xoy为总体坐标系，o为坐标原点.xkokyk为每个微裂纹对应的局部坐标系，ok为坐标原点.为了方便描述，将图2 中的问题记为原问题.由于原问题中存在多条微裂纹，并且微裂纹的位置和角度是任意的，现利用逐步递推法将原问题转化为多个子问题(参见图3 ～ 5)，即子问题1、子问题2、子问题3、子问题4 等，通过逐一求解子问题中的主裂纹和微裂纹的应力场得到原问题的解.

图2 无限大平面内含一个主裂纹和多个任意分布的微裂纹Fig. 2 An infinite plane containing a macro crack and multiple micro cracks

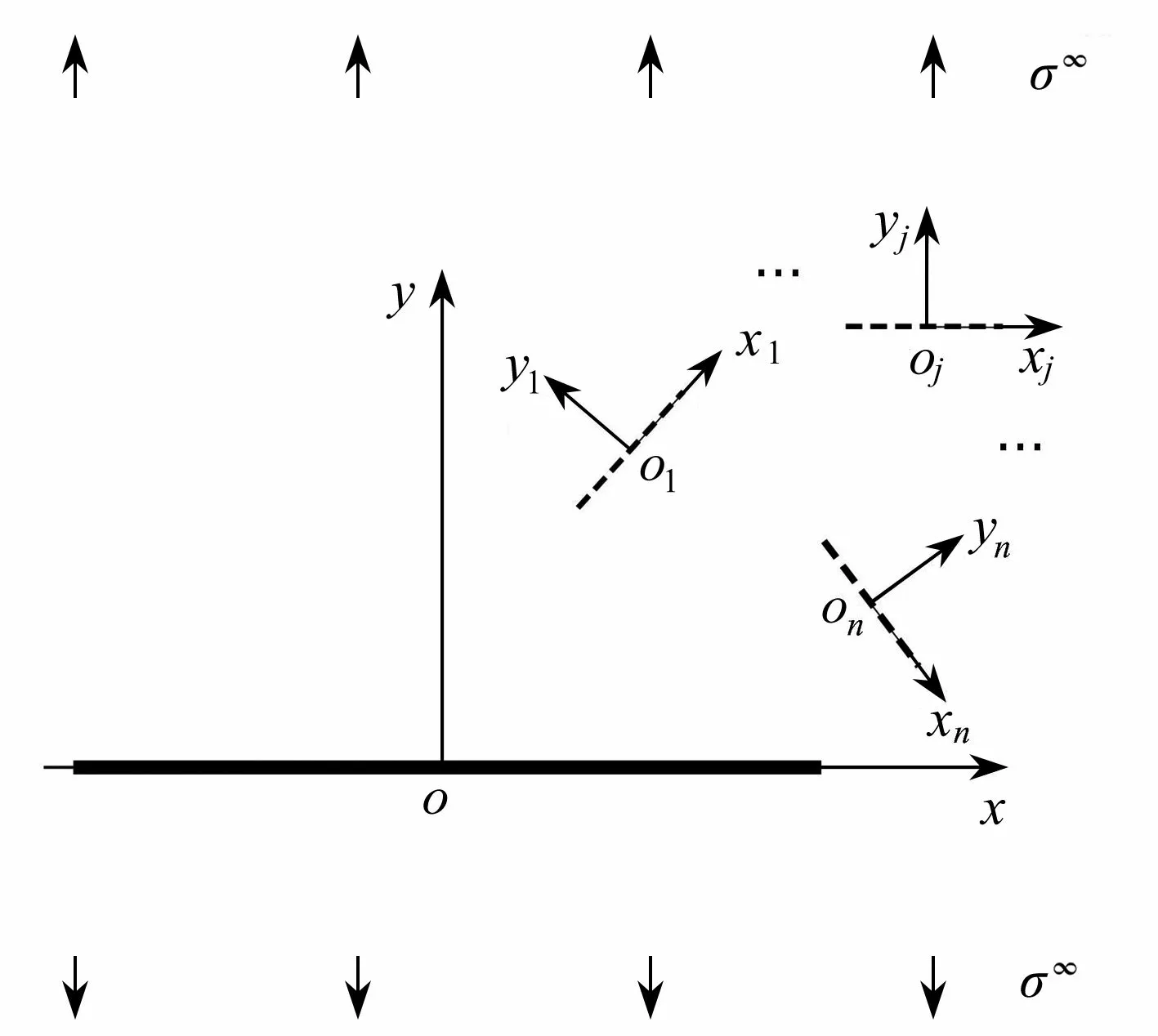
图3 子问题1：只有主裂纹、远场有均匀拉伸载荷σ∞Fig. 3 Sub-problem 1: the macro crack under uniform tensile load σ∞

根据Muskhelishvili 复变函数法，平面内任意一点的应力与两个复应力解析函数Φ(z)，Ψ(z)和它们的导数的关系可以表示为[17]

式中，用复变量z=x+ iy代替实变量x和y，σxx和σyy分别为水平方向和垂直方向的正应力，τxy为切应力；(¯·)表示Φ(z)，Ψ(z)和z的共轭值；(·)′和(·)″分别表示Φ(z)和Ψ(z)的一阶导数值和二阶导数值.

1.1.1 子问题1

在无限大平面内含一条主裂纹、没有微裂纹、远场有均匀拉伸载荷σ∞，如图3 所示.图中实线代表真实存在的裂纹，虚线代表非真实存在的裂纹，将位于主裂纹尖端周围的任意一条微裂纹记为微裂纹j(j=1, 2, ··· ,n).主裂纹的半长为a，微裂纹j的半长为aj，主裂纹尖端到微裂纹j中心的距离为dj，微裂纹j自身的倾斜角度为βj，微裂纹j相对于主裂纹尖端的方位角为θj.另外，βj和θj的正方向为逆时针方向.

实际上，子问题1 就是著名的Griffith 裂纹问题，Muskhelishvili 给出的复应力解析函数表达式如下[17]：

图4 子问题2：任意多条微裂纹Fig. 4 Sub-problem 2: the micro cracks

当第j条微裂纹上作用有集中力时，集中力F的大小与子问题1 中得到的微裂纹j处的法向应力和切向应力相等，方向相反，集中力的表达式为

1.1.3 子问题3

无限大平面内含一条中心主裂纹、没有微裂纹、在远处不受力，如图5 所示.即求解主裂纹在非均匀分布载荷F作用下，在总体坐标系下的应力场.其中，F的大小等于子问题2 中主裂纹位置处的应力，方向与原方向相反：

图5 子问题3：只有主裂纹Fig. 5 Sub-problem 3: the macro crack

1.1.4 子问题4

以上推导的理论方法有三个优点：第一，在推导过程中没有引入其他有特殊含义的参数，因此适合求解线弹性断裂力学范围内的平面裂纹问题；第二，对微裂纹的数量和位置没有限制，当研究多裂纹问题或裂纹的分布问题时，只需要修改裂纹的位置参数，而不需要重新建模或划分网格，这为研究工作节省了计算时间，提高了效率；第三，在求解过程中考虑了微裂纹间的相互影响，减小了计算误差，补充了平面多裂纹问题的理论解.

1.2 裂纹尖端损伤区

以往的模型描述损伤的方法是定义一个标量、矢量或张量作为损伤状态变量，但实际上一点的损伤状态是很复杂的[14-16,19-20].本文放弃上述损伤变量，把裂纹尖端作为一点的损伤状态，将损伤区内微裂纹对主裂纹尖端应力场的影响用损伤参量描述，即损伤变量描述的是主裂纹尖端所有的损伤情况(微裂纹的倾斜角、方位角、数量等因素).当远场拉伸载荷为σ∞时，假设材料为各向同性，并且不考虑微裂纹扩展过程中的各向异性力学特性.在单轴拉伸情况下，主裂纹尖端的损伤变量DMA可以定义为

式中，DMA表示主裂纹尖端损伤的大小以及微裂纹对主裂纹尖端损伤的影响，KⅠMA表示主裂纹尖端的应力强度因子.一般情况下，损伤参量DMA的值介于0 到1 之间.当微裂纹数量为零时，DMA也为零，裂纹受到的载荷等于远场的应力.当DMA的值大于零时，代表损伤区的微裂纹对主裂纹尖端损伤有增强作用，即微裂纹的存在使得主裂纹的应力强度因子增加并且更容易发生扩展.当损伤参量的值小于零时，代表损伤区的微裂纹对主裂纹尖端的应力强度因子有屏蔽作用.

类似地，微裂纹尖端的损伤参量可以表示为

1.3 方法验证

图6 展示了共线微裂纹对主裂纹尖端应力强度因子的影响.为了验证前两小节的求解，以图6(a)所示的问题为例，建立相应的有限元模型如图7 所示.其中，主裂纹为AB，裂纹半长为a，微裂纹半长为a1，a/a1=1，β1=0，θ1=0.材料的弹性模量是210 GPa，Poisson 比是0.3，这里不考虑塑性，是静态的弹性计算.单元类型是Plane 183.裂纹尖端采用奇异性单元，求解裂纹尖端的应力强度因子采用的是位移外推法.

图6 共线微裂纹对主裂纹尖端应力强度因子的影响：(a) 无限大平面内的共线裂纹；(b) 裂纹尖端B 点的应力强度因子随裂纹间距的变化Fig. 6 I nfluence ofthecollinearmicrocrackon thestressintensity factor of the macro crack tip: (a) a collinear micro crack and a macro crack in an infinite plane;(b) KB/(σ∞)vs. d/a1fora/a1=1undertensile load

图7 共线裂纹的有限元模型：(a) 整体网格；(b) 裂纹附近网格；(c) 裂纹尖端附近网格Fig. 7 The finite element method (FEM) for the collinear crack: (a) the whole FEM mesh; (b) the FEM mesh around the crack;(c) the FEM mesh near the crack tip

以图6(a)中的共线裂纹为例，图8(a)和8(b)分别展示了子问题1 和子问题3 中主裂纹上的正应力在裂纹面上的变化曲线.横坐标表示主裂纹长度方向的坐标值，从左至右分别表示主裂纹左尖端和右尖端.结果显示：主裂纹右尖端受微裂纹的影响，其应力的绝对值相比主裂纹左尖端更大.对比子问题1 和子问题3 可知，主裂纹上最大应力值的绝对值由29 MPa 减小到0.24 MPa，下降了99.2%.当计算到子问题5 时，主裂纹上的应力相比子问题3 下降了99.996%.随着子问题增加，主裂纹上的应力值将越来越小.因此，为了提高计算效率，在实际应用中可以只计算到子问题5.

图8 主裂纹上的正应力在裂纹面上的变化曲线：(a) 子问题1；(b) 子问题3Fig. 8 The normal stress on the crack surface of the macro crack: (a) sub-problem 1; (b) sub-problem 3

2 损伤区的微裂纹对主裂纹尖端损伤的影响

2.1 微裂纹的分布对主裂纹尖端损伤的影响

以往的文献表明，微裂纹相对主裂纹尖端的方位角对主裂纹尖端的应力强度因子有较大的影响[1].事实上，当主裂纹尖端附近存在多条微裂纹时，微裂纹的分布方式、数量、方位及倾斜角度等均对主裂纹尖端应力场有影响.下面以两种链式分布的微裂纹群为例，分析微裂纹对主裂纹尖端损伤的影响.

2.1.1 链式分布

图9 中含一条有限长的主裂纹和k(k=1, 2, ···, 14)条正向链式分布的微裂纹.主裂纹的半长为a，微裂纹的半长为ak，微裂纹与主裂纹的长度取为ak/a=0.1.微裂纹群相对于x轴对称分布，x轴上方微裂纹的方位角θk(k=1, 2, ···, 7)=20°，25°，15°，20°，15°，10°，5°，其他参数参见表1 和2.

图9 无限大平面内含一条主裂纹和链式分布的微裂纹，在无限远处有均匀拉伸应力Fig. 9 An infinite plane with a macro crack and chain-distribution micro cracks under tensile load

表1 主裂纹尖端到微裂纹中心的距离 dk/a (k=1, 2, ···, 7)Table 1 The distance dk/a (k=1, 2, ···, 7) between the macro crack and each micro crack

图10(a)是主裂纹右尖端的损伤参量随微裂纹倾斜角度的变化曲线，β1与βk(k=2, 3, ···, 7)的关系参见表2.结果显示：随着微裂纹群与主裂纹尖端的距离或微裂纹的倾斜角度减小，微裂纹对主裂纹尖端损伤的影响逐渐增大，使得主裂纹更容易发生扩展.

表2 微裂纹的倾斜角度βk (k=1, 2, ···, 7)Table 2 The inclination angle βk (k=1, 2, ···, 7) of each micro crack

图10(b)是微裂纹左尖端的损伤参量随微裂纹倾斜角度的变化曲线，距离参数为d1/a=0.2.结果显示：微裂纹的倾斜角度较小时，对裂纹尖端的损伤有增强作用；随着倾斜角度增大，微裂纹尖端的增强作用逐渐过渡为屏蔽作用.

2.1.2 反向链式分布

图11 中微裂纹与主裂纹的长度比为ak/a=0.1.微裂纹关于x轴对称，x轴上方微裂纹的方位角θk(k=1, 2, ···,7)=40°，30°，20°，10°，15°，10°，5°，其他参数见表3 和4.

表3 主裂纹尖端到微裂纹中心的距离 dk/a (k=1, 2, ···, 7)Table 3 The distance dk/a (k=1, 2, ···, 7) between the macro crack and each micro crack

图10 微裂纹是正向链式分布时，损伤参量D 随β1 的变化，d1/a=0.2：(a) DMA；(b) DMIFig. 10 Damage parameter D vs. inclination parameter β1 for chain-distribution micro cracks, d1/a=0.2: (a) DMA; (b) DMI

图11 无限大平面内含一条主裂纹和反向链式分布的微裂纹，在无限远处有均匀拉伸应力Fig. 11 An infinite plane with a macro crack and reversed chain-distribution micro cracks under tensile load

图12(a)是主裂纹右尖端的DMA的值随微裂纹倾斜角度β1的变化曲线.β1与βk(k=2, 3, 4, 5, 6, 7)的关系参见表4.结果显示：随着微裂纹倾斜角度或微裂纹与主裂纹尖端距离的减小，DMA的值增大.通过对比图10(a)和12(a)发现，当反向链式分布的微裂纹群存在于主裂纹尖端附近时，对主裂纹尖端损伤的增强作用更大，主裂纹更容易发生扩展.图12(b)是微裂纹左尖端的DMI随微裂纹倾斜角度β1的变化曲线.结果显示：微裂纹4 与主裂纹尖端的距离最近，其DMI的值较大；微裂纹7 与主裂纹尖端的距离较远，其DMI的值较小.

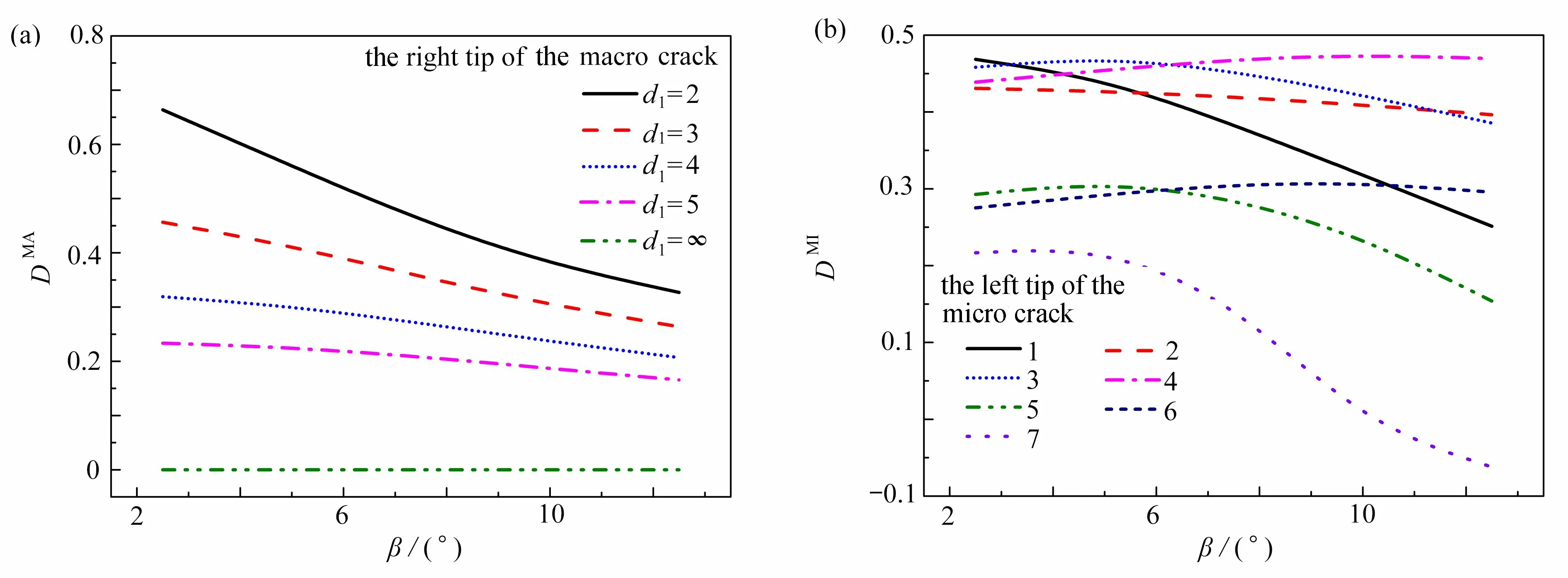
图12 微裂纹是反向链式分布时，损伤参量D 随β1 的变化，d1/a=0.2：(a) DMA；(b) DMIFig. 12 Damage parameter D vs. inclination parameter β1 for reversed chain-distribution micro cracks, d1/a=0.2: (a) DMA; (b) DMI

表4 微裂纹的倾斜角度 βk (k=1, 2, ···, 7)Table 4 The inclination angle βk (k=1, 2, ···, 7) of each micro crack

通过以上分析可知，微裂纹的倾斜角度对主裂纹尖端作用效应的强弱和性质起决定性的作用.其次，当微裂纹与主裂纹尖端的距离较近时，主裂纹尖端产生的损伤较大.随着距离增加，损伤减小.

2.2 微裂纹的分布对主裂纹扩展的影响

如图13 所示，根据脆性材料裂纹尖端损伤的程度，裂纹尖端的损伤可以分为三个区域，从外到里依次为无损区、连续损伤区和损伤局部化带[24].其中，连续损伤区是在主裂纹尖端周围存在的一个微裂纹稳定扩展的过程区.类似于金属材料中裂纹尖端的塑性区，连续损伤区内的尺寸远小于主裂纹尺寸.微裂纹损伤区表征了微裂纹的信息，标志着材料局部开始劣化.因此，研究连续损伤区内微裂纹对主裂纹尖端损伤状态的影响对了解材料局部的损伤状态有重要意义.另外，根据脆性损伤与外应力的关系可知[24]，外载荷卸载后的剩余变形很小，裂纹尖端极小区域内仍表现出良好的弹性性质，损伤区内的应力仍为K场分布，因此损伤区内裂纹尖端的损伤情况仍可用裂纹尖端的K因子进行分析.

图13 静止裂纹尖端的损伤分区结构Fig. 13 The damage zoning structure of the static crack tip

现将长度相等的微裂纹均匀分布在连续损伤区内，令微裂纹的倾斜角度的绝对值分别在30o、30o至60o以及60o至90o范围内，分析当损伤区内分别有四条微裂纹和八条微裂纹时，主裂纹尖端的损伤参量随微裂纹长度的变化，如图14(a)和14(b)所示.结果显示：当微裂纹的倾斜角度的绝对值小于等于30°时，微裂纹群对主裂纹尖端损伤的增强作用随着微裂纹的长度和数量增加而逐渐增大.同时，随着微裂纹数量增加，微裂纹对主裂纹尖端损伤的影响也明显增大.

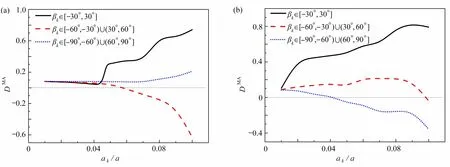
图14 微裂纹在连续损伤区内均匀分布时，损伤参量DMA 随ak/a 的变化：(a) 4 条微裂纹；(b) 8 条微裂纹Fig. 14 Damage parameter DMA vs. micro crack length ak/a for evenly distributed micro cracks: (a) 4 micro cracks; (b) 8 micro cracks

现将长度相等且倾斜角度相等的微裂纹均匀分布在连续损伤区内，分析主裂纹的损伤参量随微裂纹长度的变化，如图15 所示.结果显示：当有4 条或8 条微裂纹时，倾斜角度较小的微裂纹对主裂纹尖端损伤有增强作用，并且增强作用随着微裂纹的长度增加而增大；随着微裂纹的数量增加，主裂纹尖端损伤的增强作用逐渐增大.因此，对于均匀分布在连续损伤区内的微裂纹而言，微裂纹的数量、长度和倾斜角度均对主裂纹尖端损伤有重要影响.其中，微裂纹的数量对主裂纹尖端损伤的影响最大，其次是微裂纹的倾斜角度，最后是微裂纹的长度.

图15 损伤参量随微裂纹长度的变化：(a) βk=15°；(b) βk=45°；(c) βk=60°Fig. 15 Damage parameter DMA vs. micro crack length for evenly distributed micro cracks: (a) βk=15°; (b) βk=45°; (c) βk=60°

3 结 论

本文通过Muskhelishvili 复变函数法和逐步递推法，得到了无限大平面内包含一个主裂纹和多个任意分布微裂纹的数值解，并进行了验证.此外，本文重新定义了单轴拉伸条件下主裂纹和微裂纹尖端的损伤参量，通过分析微裂纹对主裂纹尖端损伤的影响，得出如下结论：

1) 正向链式和反向链式分布的微裂纹均对主裂纹尖端损伤有增强作用，并且随微裂纹的倾斜角度和裂纹间距的减小而增强；

2) 随着微裂纹群与主裂纹尖端的距离增大，微裂纹对主裂纹尖端损伤的影响逐渐减弱；

3) 当微裂纹的倾斜角度较小时，主裂纹和微裂纹尖端损伤均有增强作用；

4) 在连续损伤区内，均匀分布的微裂纹对主裂纹尖端损伤的增强作用随着微裂纹的数量增加而增大.

致谢 本文作者衷心感谢成都工业学院引进人才科研启动项目(2022RC005)对本文的资助.

参考文献（ References ） ：

［1］LI X T, LI X, JIANG X Y. Influence of a micro-crack on the finite macro-crack[J].Engineering Fracture Mechanics, 2017, 177: 95-103.

［2］GONG S X, HORII H. General solution to the problem of micro-cracks near the tip of a main crack[J].Journal of the Mechanics & Physics of Solids, 1989, 37（1）: 27-46.

［3］GONG S X, MEGUID S A. Microdefect interacting with a main crack: a general treatment[J].International Journal of Mechanical Sciences, 1992, 34（12）: 933-945.

［4］GONG S X. On the main crack-microcrack interaction under mode Ⅲ loading[J].Engineering Fracture Mechanics, 1995, 51（5）: 753-762.

［5］PETROVA V E, TAMUZS V, ROMALIS N. A survey of macro-microcrack interaction problems[J].Applied Mechanics Reviews, 2000, 53（5）: 117-146.

［6］PETROVA V E. Interaction between a main crack and inclusions of a given orientation[J].Mechanics of Composite Materials, 1988, 24（3）: 288-294.

［7］PETROVA V E. Modified model of macro-microcrack interaction[J].Theoretical & Applied Fracture Mechanics,1999, 32（2）: 111-117.

［8］LI X T, LI X, YANG H D, et al. Effect of micro-cracks on plastic zone ahead of the macro-crack tip[J].Journal of Materials Science, 2017, 52（1）: 1-14.

［9］ 夏晓舟, 章青, 乔丕忠, 等. 裂纹间作用机制探讨及微裂纹区对主裂纹的作用效应研究[J]. 应用数学和力学, 2010,31（1）: 61-70. （XIA Xiaozhou, ZHANG Qing, QIAO Pizhong, et al. Interaction between cracks and effect of micro-crack zone on main crack tip[J].Applied Mathematics and Mechanics, 2010, 31（1）: 61-70.（in Chinese））

［10］ 李亚, 易志坚, 王敏, 等. 裂纹面局部均布荷载下Ⅰ型裂纹有限宽板应力强度因子[J]. 应用数学和力学, 2020, 41（10）:1083-1091. （LI Ya, YI Zhijian, WANG Min, et al. The stress intensity factor of a finite width plate with a mode-Ⅰ center crack subjected to uniform stress on the crack surface near the crack tip[J].Applied Mathematics and Mechanics, 2020, 41（10）: 1083-1091.（in Chinese））

［11］CHESSA J, SMOLINSKI P, BELYTSCHKO T. The extended finite element method (XFEM) for solidification problems[J].International Journal for Numerical Methods in Engineering, 2002, 53（8）: 1959-1977.

［12］SOH A K, YANG C H. Numerical modeling of interactions between a macro-crack and a cluster of microdefects[J].Engineering Fracture Mechanics, 2004, 71（2）: 193-217.

［13］OUINAS D, BOUIADJRA B B, BENDERDOUCHE N, et al. Numerical modelling of the interaction macro-multimicrocracks in a plate under tensile stress[J].Journal of Computational Science, 2011, 2（2）: 153-164.

［14］KACHANOV L. Time of the rupture process under creep conditions[J].Doklady Akademii Nauk SSSR, 1958, 8:26-31.

［15］RABOTNOV Y N, LECKIE F A, PRAGER W. Creep problems in structural members[J].Journal of Applied Mechanics, 1970, 37（1）: 249-250.

［16］LEMAITRE J. A continuous damage mechanics model for ductile fracture[J].Transactions of the ASME Journal of Engineering Materials and Technology, 1985, 107（1）: 83-89.

［17］MUSKHELISHVILI N I.Some Basic Problems of the Mathematical Theory of Elasticity[M]. Berlin: Springer Science & Business Media , 1977.

［18］ 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003. （FAN Tianyou.The Theory of Fracture Mechanics[M].Beijing: Science Press, 2003. （in Chinese））

［19］KRAJCINOVIC D. Constitutive equations for damaging materials[J].Journal of Applied Mechanics, 1983,50（2）: 355-360.

［20］CHOW C L, WANG J. An anisotropic theory of elasticity for continuum damage mechanics[J].International Journal of Fracture, 1987, 33（1）: 3-16.

［21］TANAKA K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis[J].Engineering Fracture Mechanics, 1974, 6（3）: 493-507.

［22］KACHANOV M. Elastic solids with many cracks and related problems[J].Advances in Applied Mechanics, 1993,30: 259-445.

［23］MURAKAMI Y, KEER L M. Stress intensity factors handbook[J].Journal of Applied Mechanics, 1993, 60（4）:1063-1063.

［24］ 冯西桥. 脆性材料的细观损伤理论和损伤结构的安定分析[D]. 博士学位论文. 北京: 清华大学, 1995. （FENG Xiqiao.Micro-failure theory for brittle materials and shakedown analysis of structures with damage[D]. PhD Thesis.Beijing: Tsinghua University, 1995. （in Chinese））