炭黑填充天然橡胶材料动态非线性特性研究
2022-02-01伍佳易朱田鑫
伍佳易 朱田鑫
(株洲时代新材料科技股份有限公司,湖南 株洲 412000)
炭黑具有特殊的表面性能和胶态性质,是目前橡胶工业中性能最好、用量最大的补强剂[1]。炭黑的添入大幅度提高了橡胶的模量、拉伸强度、撕裂强度、抗疲劳性能以及抗磨损磨耗性能等[2-3]。炭黑对橡胶材料的增强效应受粒子尺寸、含量以及加载条件的影响,其中含量的影响较大。在橡胶中加入炭黑粒子可以显著增强材料的各种机械性能,拓宽材料的使用范围和工程领域。但是加入炭黑填料的同时也会使材料表现出更复杂的特性,例如黏滞损耗、应力软化和Payne效应等。
填充橡胶材料的非线性特性是减振和轮胎领域非常值得关注的问题。探究填充橡胶在不同加载条件下材料的非线性特性,对认识材料、设计材料和提高减振、轮胎产品性能具有重要作用。
1 不同温度和频率下的Payne效应
一般采用动态热机械分析仪(DMA)对填充橡胶材料的动态力学特性进行测试。湘潭大学的研究人员使用Gabo Eplexor 500N机器研究了不同温度和频率下填充橡胶材料的动态非线性特性,结果如图1~图4所示[4]。图1和图2为材料在不同温度下的应变幅值扫描测试结果,结果显示,在不同测试温度下,材料的储能模量随应变幅值的增大而变小,损耗模量先增大后变小,即在所有测试温度条件下,材料呈现了典型的Payne效应。当温度高于0 ℃时,材料的储能模量和损耗模量随温度的降低稍有提高,而储能模量和损耗模量的应变幅值依赖性受温度变化的影响较小。当温度低于0 ℃时,材料的储能模量和损耗模量随温度的降低急剧增加,而材料的Payne效应随温度的降低得到增强,特别是当温度为-30 ℃时,材料呈现了显著的Payne效应。已有研究表明,温度升高会导致填充橡胶的结合胶变少,因此,Payne效应的变化可能与填料网络破坏速率的增加和固定化天然橡胶分子链的迁移性增加有关。当温度高于0 ℃时,橡胶分子链的运动随着温度的升高变得更剧烈,这使固定的分子链恢复到自由状态,Payne效应主要归因于填充物网络的解缠;当温度低于0 ℃时,随着温度的下降,橡胶分子链的运动变得困难,固定的分子链数量增加,填料与橡胶的相互作用更强烈。因此,随着温度降低,模量增加且Payne效应得到增强。在这种情况下,Payne效应是由填料网络的解缠和固定的天然橡胶分子链的运动导致的。另外,填充橡胶材料在-30 ℃出现了显著的Payne效应。众所周知,-25 ℃是炭黑填充天然橡胶的结晶温度,低温结晶在材料内部形成结晶网络,会显著提高模量,同时结合胶的数量也会增加。因此,在-30 ℃的低温下,由于天然橡胶分子链的结晶,因此材料的模量增加,同时材料的Payne效应也会增强。
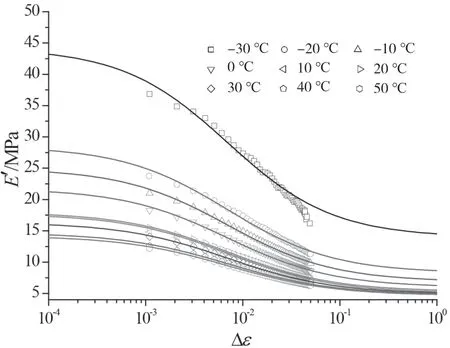
图1 不同温度下的储能模量E'与应变幅值Δε的关系曲线(散点为试验数据,实线为拟合曲线)
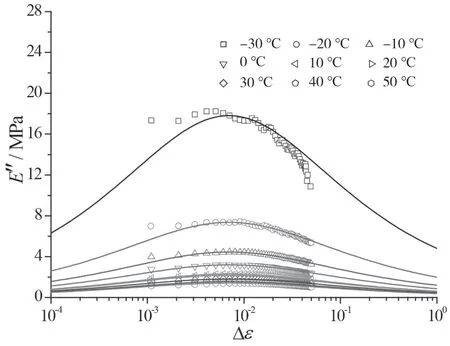
图2 不同温度下的损耗模量E″与应变幅值Δε的关系曲线(散点为试验数据,实线为拟合曲线)
炭黑填充天然橡胶在不同频率下的Payne效应如图3和图4所示。从图3和图4中可以看出,随着应变幅值的增加,储能模量降低,损耗模量先增后减,Payne效应清晰可见。众所周知,损耗模量与填料结合键的断裂率成正比。在曲线的上升阶段,由于存在足够的填料结合键,因此能量损失随应变幅值的增加而增加,而在曲线的下降阶段,由于填料结合键的数量明显减少,因此能量损失随应变幅值的增加而降低。试验结果表明,当频率增加时,Payne效应稍有增强,但是变化不是很大。同时还可以观察到,当应变幅值较小时,储能模量的频率依赖性强于应变幅值较大的情况。其原因可能是在较小的应变幅值下,存在足够的填料结合键,当频率改变时,填料结合键的数量急剧变化,因此,储能模量对频率变化敏感。随着应变幅值的增加,填料结合键的数量变少,因此频率对储能模量的影响逐渐变小。
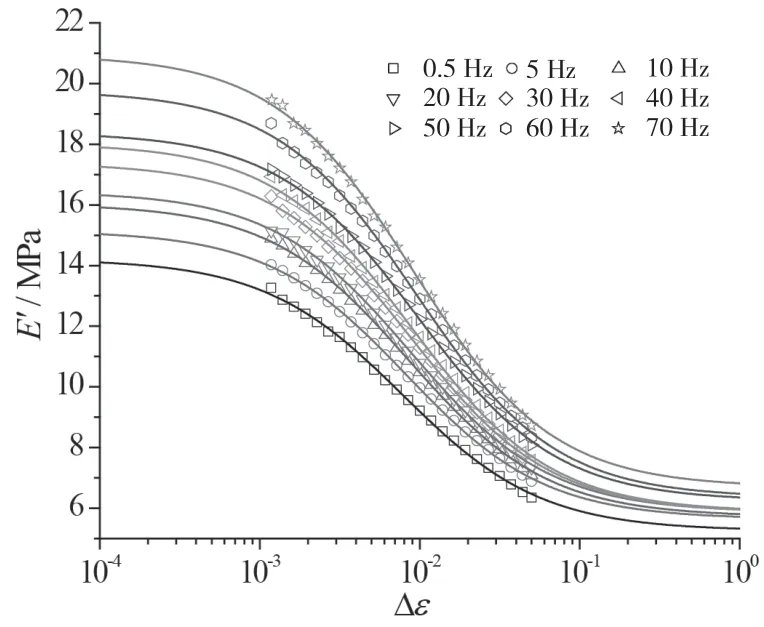
图3 不同频率下的储能模量E'与应变幅值Δε的关系曲线(散点为试验数据,实线为拟合曲线)
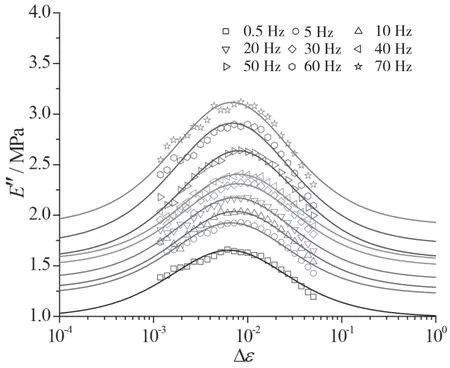
图4 不同频率下的损耗模量E″与应变幅值Δε的关系曲线(散点为试验数据,实线为拟合曲线)
2 温度和频率对Payne效应的影响机理
Maier-Göritz模型是Maier和Göritz基于橡胶与填料的相互作用而提出的,该模型可以在分子层面对橡胶材料的Payne效应进行解释。当纳米填料与橡胶材料混合时,橡胶分子链吸附在填料表面,就会形成稳定键和不稳定键。形成的这些键与Payne效应直接相关。当对系统施加力或者温度升高时,这些不稳定的键可能会断裂,如公式(1)所示。

式中:E'为储能模量;T为温度;kB为玻尔兹曼常数;N为填充化合物的网络密度。
填充化合物的网络密度N如公式(2)所示。

式中:Nc为化学交联密度;Nst为单位体积材料由稳定键形成的弹性活性链的数量;Ni为单位体积材料由不稳定键形成的弹性活性链的数量。
储能模量E'(Δε)和应变幅值Δε之间的关系如公式(3)所示。

式中:E'st是Δε为无穷大时的E'值,E'st=(Nc+Nst)kBT;E'
i 是Payne效应的幅值,E'i=NikBT;c为材料参数,它与填料表面上分子链的吸附速率和解缠速率有关。
损耗模量E(''Δε)与应变幅值Δε之间的关系如公式(4)所示。

式中:E″st为Δε趋于无穷大或趋于0时的E″值;E″i为E″的变化幅度置。
利用Maier-Göritz模型拟合储能模量与损耗模量随温度变化的试验结果。拟合曲线为图1和图2中的实线,由图1和图2可知,拟合效果很好。Payne效应在-30 ℃~50 ℃的拟合结果表明,极限储能模量的Est'值略有下降,而Payne效应幅度的Ei'值最初随温度的升高而急剧降低,然后随温度的升高保持不变,如图5和图6所示,这些变化表明温度对Payne效应的影响可分为2个阶段,这与理论结果相符。
由公式(3)可知,Ei'由材料的不稳定键密度Ni决定,而Est
'由给定温度下的参数Nc+Nst决定。如图5和图6所示,参数Ni随着温度的升高而急剧下降,而参数Nc+Nst的变化则非常微弱。这些结果表明,不稳定键因温度升高很容易断裂,从而导致与温度有关的Payne效应。另外,当温度高于0 ℃时,Ni和Nc+Nst的值变得非常小,不论温度如何变化,这2个值几乎保持不变。这表明在该温度范围内结合胶几乎不发生改变。因此,在这样的温度范围内,Payne效应主要是由填料网络的解缠引起的。当温度低于0 ℃时,Ni的数量会随着温度的降低而急剧增加,尤其是当温度为-30 ℃时,填料与橡胶之间的相互作用更强,从而提高了试验材料的模量,并且此时材料的Payne效应得到了增强。
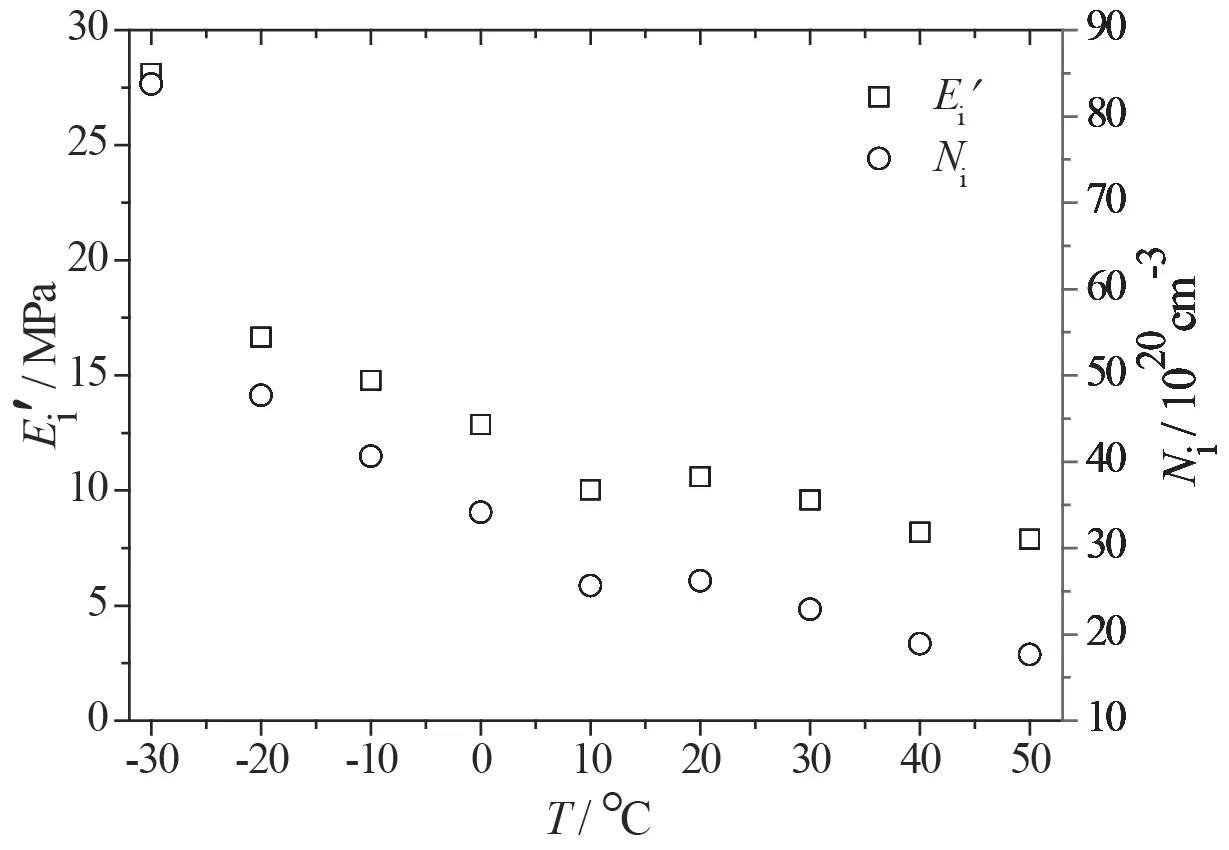
图5 参数和Ni随温度的变化

图6 参数和Nc+Nst随温度的变化情况
图2给出了Maier-Göritz模型拟合损耗模量随温度变化的结果。该模型可以很好地拟合试验结果,但是无法描述曲线的不对称特征。
温度对Payne效应的影响有2个阶段:1) 当温度低于0 ℃时,在较小的应变幅值下,储能模量随温度的降低而明显增加,特别是当温度为-30 ℃时,还可以观察到Payne效应明显增强。众所周知,橡胶材料的结晶温度为-25 ℃,在结晶温度附近,橡胶内部会形成一种结晶网络,分子链结晶抑制链段运动,从而显著提高材料的模量,增强材料的Payne 效应。2) 当温度高于0 ℃时,储能模量随温度升高略有增加。在不同温度下的Payne效应是由2个不同的因素(填料网络和结合胶)引起的。当温度高于0 ℃时,Payne效应主要归因于填料与填料之间的相互作用,而固定的天然橡胶链在温度降低至0 ℃以下时发挥越来越重要的作用。Maier-Göritz模型的拟合结果与试验数据吻合,该模型很好地解释了Payne效应的温度依赖性。
利用Maier-Göritz模型拟合不同频率下的Payne效应,如图3和图4中的实线所示,拟合结果与试验结果吻合较好。拟合结果表明,Ei'随频率的增加而增加(图7),而Est'值则变化微小。小应变幅值下储能模量的频率依赖性比大应变幅值强(图8),Nc+Nst随频率的变化不明显,这决定了Est'的变化同样也不明显。Est''和Ei
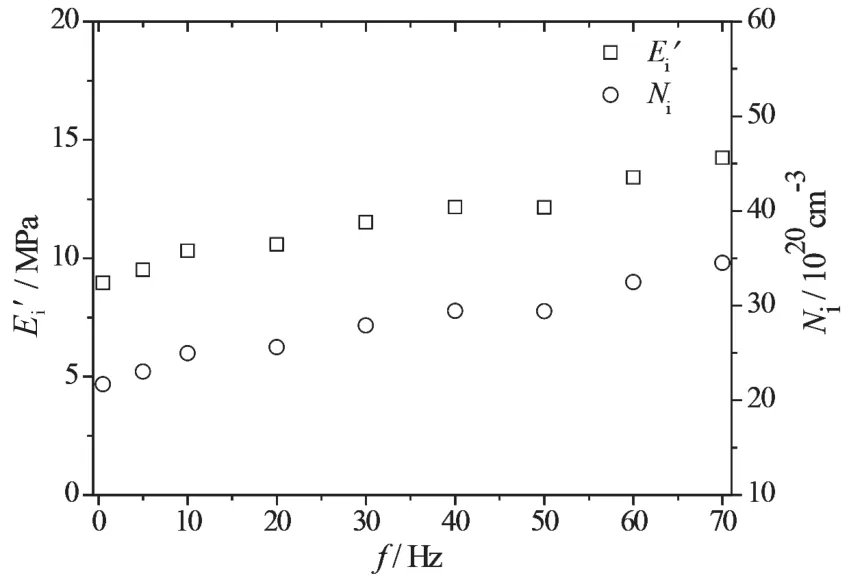
图7 参数和Ni随频率的变化
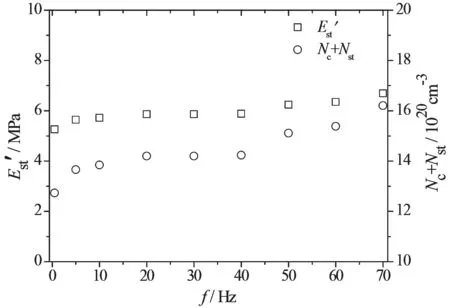
图8 参数Est'和Nc+ Nst随频率的变化
''都随频率的增加而线性增加,即随着频率变高,材料中的不稳定键越来越多。结果表明,由于频率变高,因此导致材料中不稳定键的数目增加,从而使Payne效应得到增强。
考虑频率对Payne效应的影响。对较小的应变幅值来说,其储能模量的频率依赖性强于应变幅值较大的情况。根据Maier-Göritz模型的拟合结果可以得出,Payne效应随频率的增加而增加是由材料不稳定键的增加导致的。Maier-Göritz模型的拟合结果与试验数据吻合,并且很好地解释了Payne效应的频率依赖性。
3 结语
不同温度和频率下填充橡胶材料的Payne效应测试结果表明,温度对Payne效应的影响呈现2个特点:1) 当温度低于0 ℃时,储能模量和损耗模量随温度的降低而增加,其应变幅值依赖性得到增强,特别是当温度为-30 ℃时,可以观察到显著的Payne效应。2) 当温度高于0 ℃时,储能模量和损耗模量随温度的降低略有增加,温度对材料Payne效应的影响较小。频率对Payne效应的影响,对应变幅值较小的情况来说,其储能模量的频率依赖性强于应变幅值较大的情况。利用Maier-Göritz模型探索Payne效应的温度和频率的相关性发现,Payne效应的产生是由2个因素(填料网络和结合胶)引起的。当温度高于0 ℃时,Payne效应主要归因于填料与填料之间的相互作用,而结合胶在温度降至0 ℃以下时发挥了重要的作用。当频率不同时,材料不稳定键的增加会导致Payne效应随频率的增加而增强。
