马蹄形TBM超挖控制技术研究

张永生，张克良，宋朝瑞，刘睿斐

(中铁工程装备集团有限公司，河南 郑州 450016)

非圆形断面开挖一直以来是隧道掘进机结构与控制设计的难点，尤其是非圆形硬岩断面开挖，此类断面开挖往往以圆形开挖面为基础，然后再进行针对性的补充开挖，补充开挖过程需要经过多次磨合才能形成最终的开挖面。虽有理论设计方案，但尚无应用于硬岩非圆形断面开挖的TBM 施工案例，控制技术也鲜有研究。

随着矩形顶管机以及马蹄形盾构的成功应用，用于非圆形断面开挖的隧道掘进机越来越受到人们的关注。马蹄形断面开挖较圆形断面可减少10%～15%的开挖面积，能够大幅降低施工成本以及出渣量，同时也提高了隧道空间利用率，国内蒙华项目在全球首次应用马蹄形盾构进行掘进施工并取得了成功。这也是马蹄形盾构工法在山岭软土隧道领域首次运用。矩形顶管机目前已有众多软土市政施工案例，对于短距离软土开挖，矩形掘进机技术已日渐成熟。

当前对非圆形开挖面的研究和应用也比较多，如类矩形顶管机、马蹄形盾构等。李建斌[1-2]介绍了当前对非圆形断面掘进机的总体研究及应用情况，基本囊括了当前非圆形断面的主流形式，无论是采用双圆型断面、还是多圆形断面、类矩形断面均通过多个圆形刀盘组合开挖实现，并研究了多刀盘空间构型及协同驱动、多维度位姿测量及纠偏、多自由度重载柔性拼装机构设计与控制等领域，解决了异形盾构施工法难题。吕强[3]介绍了偏心多轴异形断面隧道掘进机的研究与应用，重点对矩形盾构做了理论分析和研究，并结合应用进行了说明，这些研究均在软土掘进机上进行；奚鹰[4]、李海[5]等的研究亦是建立在软土地层，目前尚无适用于硬岩TBM 异型断面开挖的研究和应用[6]。主要原因是硬岩异型掘进机需要全断面开挖，开挖面不能存在盲区，不像软土盾构，开挖面可存在开挖盲区，在掘进过程中，由于软土质地柔软，开挖盲区软土受刀盘扰动以及盾壳切入影响，能够自动形成剥落，最终形成理想开挖面。异型硬岩TBM 要实现全断面开挖有两种方法：①可通过全断面扩挖实现，但此种方式会造成TBM 趋势不断下降，不能满足设计要求；②通过圆形刀盘+盲区扩挖形式实现异形断面开挖。本论文以马蹄形硬岩断面设计为依据，通过方法②实现。

按照上述设计了初步方案，对于马蹄形断面开挖采用两个步骤完成：首先进行圆形断面的开挖，然后通过控制扩挖铣挖刀在刀盘不同位置时的扩挖量，对开挖盲区进行多次的循环扩挖，直至达到理想的扩挖断面。本文另外研究了在空载试验条件下的超挖油缸位置与位移之间的控制关系，通过数学建模的方式建立超挖油缸与所处角度的实时位移函数关系，利用低成本速度与比例控制硬件进行控制测试，在测试油缸空载运行情况下实现了位移与刀盘位置的精确对应控制，空载测试效果基本理想。控制系统需要考虑控制精度、鲁棒性[7]、液压缸伸缩载荷等各种干扰，本文以空载测试为主，由于受试验条件限制未考虑时变负载以及其他耦合影响因素。

1 马蹄形TBM开挖断面概况

国内某硬岩项目需马蹄形开挖断面开挖，开挖断面图如图1 所示，开挖直径12.3m，隧道竖直中心线左右两侧对称，呈镜像关系。

图1 马蹄形开挖断面图

每段圆弧对应的半径关系如下。

R＝7 150mm，0°≤α＜116°，244°≤α＜360°。

R＝3 098mm，116°≤α＜136°，224°≤α＜244°。

R＝13 211mm，136°≤α＜224°。

内切圆半径R＝6 150mm。

2 马蹄形TBM系统设计

2.1 设计思路

从图1 可以看出，该马蹄形断面中心为一个半径R＝6 150mm 的正圆，在进行断面开挖时，可先进行一个推进行程的正圆开挖，然后再通过补充开挖的形式进行二次开挖，最终形成马蹄形断面，完成一个掘进循环。

2.2 结构设计

按照上述思路设计的刀盘正视图如图2 所示，刀盘剖视图如图3 所示。

图2 刀盘正视图

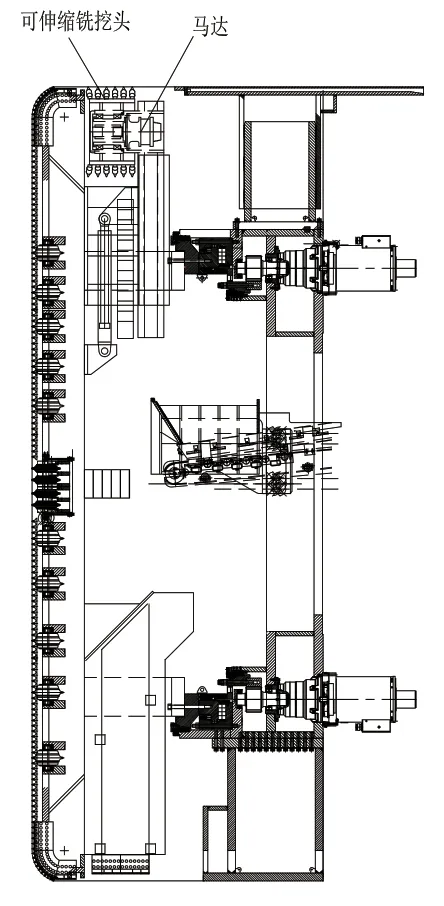
图3 刀盘剖视图

铣挖刀固定在刀盘后边，在正圆开挖阶段，铣挖刀缩回，不进行任何动作，第一阶段的正圆开挖结束后，停止推进，保持刀盘在低速旋转，控制铣刀在不同角度伸出对应的位移量，经过多次铣挖，逐渐形成马蹄形开挖断面，完成超挖，换步完成一个掘进循环。

3 控制系统设计

3.1 建立模型

3.1.1 位移与角度关系

将掘进超挖结构进行模型简化，如图4所示。

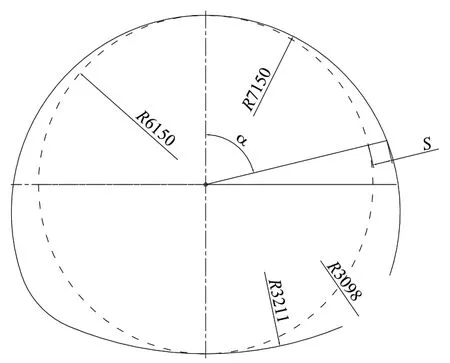
图4 简化模型图

以隧道中心为坐标原点，水平方向为x轴，竖直方向为y轴，设定刀盘位置与y轴正向夹角为0，顺时针旋转为正方向，油缸与y轴正向夹角为α。在α＝0°和180°时，可认为伸缩油缸位移为全部缩回状态，位移s＝0。刀盘旋转一周为360°，刀盘在0～360°之间往复运动。根据三角函数关系，建立油缸伸出位移s和对应角度α的关系s＝f（α）如下

绘制油缸伸出位移曲线图如图5 所示。

图5 油缸伸出位移曲线图

从图5 可以看出，该位移曲线为连续的弧形曲线，在0°时位移为0，随着角度的增加，位移越来越大，在121°时达到最大，超过121°后位移逐渐减小，直到180°时完全缩回。180°～239°时位移逐渐增加，239°时达到最大，239°～360°时位移逐渐减少直到0。

3.1.2 油缸速度与角度关系

从图中可以看出该位移曲线在每个角度对应的斜率K＝d（s）/d（α）是不断变化的。在进行超挖时，刀盘工作在匀速旋转模式下，d（α）∝d（t）；所以K＝d（s）/d（α）→k∝d（s）/d（t），即斜率k等效于伸缩油缸在不同角度的伸出或回收速度。

对s＝f（α）位移函数进行求导求出对应角度处油缸速度。

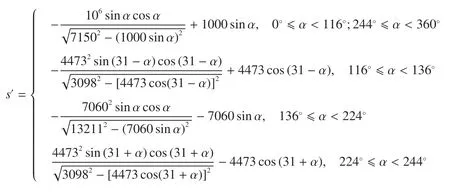
该函数为位移对角度的变化率函数，并不是伸缩油缸在不同角度对应的速度函数，需要做进一步求解处理，以求解油缸的速度函数。在超挖阶段，刀盘旋转较慢，可按照刀盘转速r＝0.2rpm 进行考虑，求出每秒旋转度数：0.2×360°/60＝1.2°/s，即一个循环的转动角度与转动时间的关系α＝1.2t，根据以上函数关系求解伸缩油缸速度v转动角度α函数关系

求得v＝1.2s′。

根据上述求得的速度v与角度α的函数关系v＝f（α），油缸速度理论曲线图如图6 所示，从图中可以看出速度值出现了负值，这是由于油缸在该角度时处于回收阶段位移差为负值。

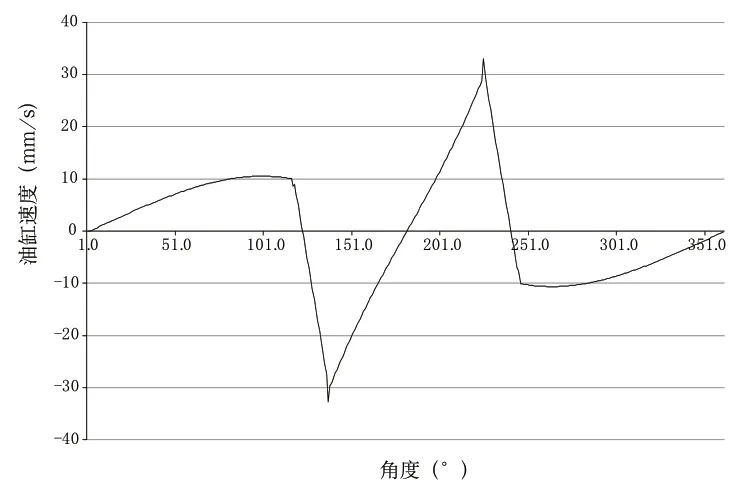
图6 油缸速度理论曲线图

为便于控制，我们将负速度取绝对值得出油缸速度控制曲线如图7 所示。

图7 油缸速度控制曲线

从图6 油缸速度理论曲线图可以看出，在一个旋转周期360°范围内，油缸的速度时刻都在变化。回收的速度明显大于伸出时的速度。油缸的速度控制可通过比例调速阀完成。

3.1.3 控制电压-油缸速度关系

在目前TBM 包含盾构上的速度控制往往通过电液比例放大电路（放大板）完成。放大板接收PLC 输出的电压控制信号，输出PWM 电流信号到比例阀，进而驱动比例阀。电压信号一般采用0～10V，输出的电流信号范围可通过软件进行设定。这种控制方式目前应用较多，但存在输出死区以及线性度问题。为找到控制电压与油缸伸出速度之间的关系，只能通过多次试验获得二者关系。

另外由于油缸的有杆腔和无杆腔面积的不同，即使所供油路的流量恒定，伸出速度与回收速度也明显不同。在对油缸的速度进行实验测试时应分别测试。

我们对用于此次实验测试油缸做了反复测试，并记录了测试数据，通过对测试数据的分析得出控制电压-油缸伸出速度的关系如图8 所示，控制电压-油缸回收速度的关系如图9 所示。

图8 控制电压-油缸伸出速度关系

图9 控制电压-油缸回收速度关系

对控制电压速度数据进行线性化处理，得出速度v与控制电压u之间的关系。

伸出速度f（v）＝5.104u+12.9

回收速度f（v）＝8.629u+24.69

由于最终控制变量为电压信号，需要将上述速度函数转化为电压信号函数如下。

伸出控制电压f（u）＝（v-12.9）/5.104

回收控制电压f（u）＝（v-24.69）/8.629

3.2 系统构成

按照上述模型建立控制系统，主要系统部件如下。

1）PLC TBM 往往采用PLC 作为控制器，可将超挖系统的控制搭载在TBM 上的PLC 上，用PLC 编程实现控制[8-10]。

2）液压系统 包含液压驱动油路以及伸缩油缸、位移传感器（可内置于油缸）、换向阀、比例调速阀、液压管路等。

3）旋转编码器 用于实时获取刀盘以及铣挖刀当前精确位置和角度。

4）电液比例控制 用于控制比例调速阀，控制油缸伸收速度[11-12]。

系统构成总图如图10 所示。

图10 系统构成总图

4 控制原理

4.1 控制原理

超挖阶段的控制也就是对伸缩油缸的控制，伸缩油缸的控制以理论伸出位移量s为基本控制目标。对于此种超挖形式的位移控制一般有3 种思路。

4.1.1 直接控制

即通过油缸位移和实际位移的偏差直接控制油缸的伸收和速度。偏差可以是一个设定的范围，如果超出设定范围就相应地启动伸收控制，使油缸位移落在需要的范围内。控制过程中换向阀会频繁切换，对管路、阀组、油缸以及机械结构冲击较大。

4.1.2 离散型PID控制

通过位移传感器形成闭环控制，将油缸实际位移和理论控制位移输入到PID 控制程序，通过PID 控制器输出伸收命令，需要设定PID 参数。由于整个过程油缸的位移和速度均在变化，会造成PID 参数也需跟随着变化，参数寻找困难。采用此方式会有滞后现象，控制过程中换向阀也会频繁切换，对管路、阀组、油缸以及机械结构冲击较大。

4.1.3 单一化动作下速度控制

通过对油缸位移函数以及位移曲线图分析可知：在一个完整的360°圆周周期内，每个超挖控制油缸都经历了4 个动作阶段：0°～121°，伸出动作阶段；121°～180°，回收动作阶段；180°～239°，伸出动作阶段；239°～360°，回收动作阶段。

1）伸出阶段 在0°～121°和180°～239°范围内，油缸的位移是随角度的增大不断增加的；可认为油缸一直处于伸出状态。可通过以下方法进行控制：在该范围内只允许伸出和停止的动作，如果油缸实际伸出位移小于理论位移，就一直维持伸出动作；如果油缸伸出位移超出理论位移就停止伸出动作。只要控制好伸出速度，伸出速度合适，就能保证油缸在任何时刻都能跟随理论位移。

2）回收阶段 同以上所述，121°～180°和239°～360°范围内油缸的位移是随角度的增大不断减小的，直至减为0；可以认为油缸一直处于缩回状态。在该范围内可通过只允许缩回和停止的动作的控制，如果油缸实际位移小于理论位移，就停止缩回动作；如果油缸实际位移超出理论位移就一直维持缩回动作。只要控制好油缸的缩回速度，就能保证油缸在任何时刻都能跟随理论位移。

上述控制方法对伸出和回收做了分段处理，在每个阶段对应每个动作控制，这就避免了伸出和回收反复调整的问题，也降低了对液压系统以及机械结构的冲击。过程的控制量也减少到只有油缸速度一个变量了，从而简化了控制系统设计。对于超挖系统的控制，我们采用方法③进行控制。

4.2 控制流程图

根据上述方法③绘制控制流程图如图11 所示。

图11 控制流程图

速度控制贯穿控制的整个过程，从理论速度函数可知，油缸的速度是随着角度的变化而时变的，对油缸的伸收控制进行了分段处理，不同的动作阶段对应不同的控制策略，也和角度相关。

5 测试验证

为验证控制方法③的可行性，对油缸进行了空载测试。

实验用测试油缸∅80/56×850mm 最大行程为850mm，12.3m 马蹄形超挖油缸最大行程为1 421mm 左右，为便于测试和验证，将马蹄形位移函数除以2 进行验证和测试，相应的速度函数也减半。比例阀规格：HAWE SEH2-3/50 FP-G 24[13]。

由于放大板输出存在控制死区，需要解决死区控制的问题。经过测试，当控制电压小于0.3V时，放大板无输出，当控制电压为0.3V 时，控制放大板开始有输出；0.3V 为死区控制阀值，为保证油缸的可靠稳定动作，设置PLC 输出到放大板的最小控制电压为0.5V。在控制电压为最小0.5V 的情况下分别对油缸的伸出和回收进行了速度测试：油缸的伸出速度最小约为17mm/s，回收速度最小约为33mm/s。

测试油缸的理论速度曲线如图12 中的曲线1。曲线2 为速度的拟合曲线。由于控制电压最小为0.5V，即油缸伸出的最小速度为17mm/s，回收速度最小约为33mm/s。我们对速度曲线进行了处理：如果伸出速度小于17mm/s，按照17mm/s 进行控制，回收速度小于33mm/s 的部分按照33mm/s进行控制，伸出速度超过17mm/s 或者回收速度超过33mm/s 的部分按照速度曲线函数进行速度赋值，修正后的速度曲线如图12 中的曲线3。

图12 速度曲线

根据油缸速度与控制电压的关系，求出各个角度的控制电压

将上述函数绘制曲线，得出不同角度下的控制电压u-α曲线图，如图13 所示。

图13 控制电压u-α曲线

按照此控制电压进行油缸控制初步测试，油缸实际位移与理论位移跟随较好，实验测出的实际位移与理论位移偏差值分布曲线如图14 所示。

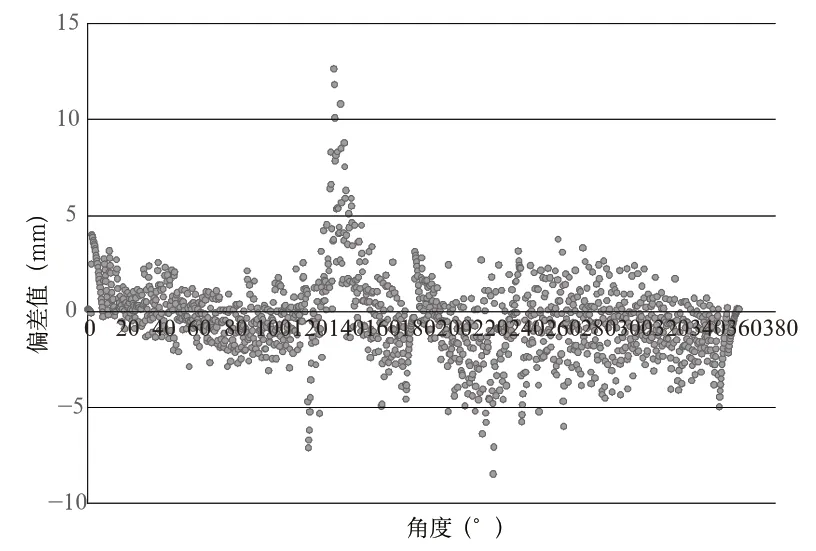
图14 偏差分布曲线

从图14 可以看出，大部分偏差均在±5mm范围内，有3 处控制存在异常偏差过大现象。

1）异常处1 121°～124°出现过量调节，回收速度过快，需要降低速度。

2）异常处2 131°～158°出现过量调节，回收速度过慢，需要提高速度。

3）异常处3 202°～232°偏差基本为负，需要提高伸出速度。

对控制电压进行局部优化，优化后电压控制参数变更如下。

优化后进行二次测试，优化后的偏差分布如图15 所示。

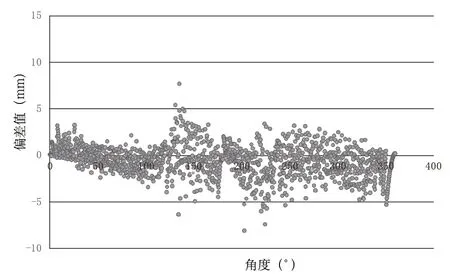
图15 优化后偏差分布曲线

经过优化后，控制精度得到了提高，实际控制位移与理论目标位移的偏差值基本均落在了±5mm 范围内，由于油缸总位移为850mm，控制精度约为：5/850 ≈6‰。控制效果较为理想。

6 结论

通过数学建模建立位移与超挖油缸位置的精确对应关系，并通过控制超挖油缸伸出和回收速度的方式来控制超挖量，在理论上是可行的。由实验得出的位移控制精度为6‰左右，该控制精度是在理想的空载实验的情况下得出的，偏理想化。不足之处：①未考虑时变负载影响；②未对4 组伸缩扩挖油缸之间的协同配合工作进行论述；③没有和液压伺服系统进行控制对比，能否应用于实际开挖，尚待进一步测试和验证。本文描述的超挖控制原理与盾构扩挖类似，均是在圆形断面上进行扩挖实现，硬岩TBM 超挖只是分了两个开挖工序进行实现。硬岩非圆断面开挖存在结构设计和控制设计双重难点，在后续研究中应优化结构设计，控制技术研究建议将变负载情况下多耦合因素影响作为重点研究内容。