网络舆情的分数阶精细化建模与应用*

曹科才 丁冬女 樊亚平

(1.南通大学 南通 226019；2. 南京工程学院 南京 211167；3.兰州大学 兰州 730000)

0 引 言

人民网舆情监测室在《2018年中国互联网舆情分析报告》中指出社会舆论的表达方式已经覆盖全媒体平台，其中“报网端媒”逐渐成为新媒体矩阵的标配，而这同时也意味着对于网络舆情的预警管控正面临着前所未有的挑战。

舆情是“舆论情况”的简称[1]，是指在一定的社会空间内围绕社会事件的发生、发展和变化，作为主体的民众对社会中各种现象、问题所表达的信念、态度、意见和情绪等外部表现的总和。随着网络的普及，人们获取信息、发布信息以及交流观点变得越来越容易，现实生活中的一件小事有可能在网络上产生较大的影响力，直接影响人们的生产以及生活，甚至同整个社会的稳定紧密联系在一起。如何准确及时的掌握舆论情况的动态演化，分析舆情未来的走向趋势，不仅具有重要的科学意义而且有助于各级政府部门制定科学合理的舆情引导管控方案，进一步营造健康和谐的网络舆情生态环境。

舆情传播速度快、舆情内容多元化、舆情传播主体特殊、舆情传播途径多样等特点为现今网络舆情的研究带来前所未有的挑战。国内外学者的研究工作总体上可以分为无模型的网络舆情研究与基于模型的舆情分析研究两个方面。无模型的网络舆情研究主要从新闻与传媒、社会学、行政管理等角度，借助于数据分析与数据处理技术(如时间序列、神经网络[2]、支持向量机[3]等)，基于获取的舆情信息以及对舆情数据的整理、分类与存储等工作，实现对网络舆情概念界定、网络舆情现象的解释，较少涉及整个网络舆情系统演化规律与演化机理的研究。文献[4]通过对网络舆情的监测与分析，提出了大数据时代网络舆情监测与分析研究中面临的一些问题; 文献[5]分析了大数据技术对于推进网络舆情研究的贡献，并讨论了大数据时代网络舆情研究可能的突破点；文献[6]以高校舆情为例，提出基于大数据技术的舆情管理策略。上述对于网络舆情的定性研究，由于缺乏舆情演化机理方面的研究，因而较难以准确刻画舆情未来走向与演化趋势。

不同于上述无模型的定性研究，近年来国内外学者从系统科学与工程的观点入手，将网络舆情系统看作一个动力系统，利用不同的动力学建模方法试图进一步挖掘舆情系统内部演化机理，以便更好的掌握网络舆情演化规律，同时为舆情趋势预测以及后期的舆情管控提供支撑。文献[7, 8]以舆情信息量为变量，以微分方程为工具通过构造合适的数学模型分析网络舆情主体间的交互形式和变化规律，并借助仿真软件实现了舆情定量描述基础上舆情趋势分析与预测。其中文献[7]以大数据背景下网络舆情热度问题为对象，通过构建合适的网络舆情热度模型，实现网络舆情热度的定量刻画与趋势预测，为舆情引导政策的制定提供了较好的参考；文献[8]借助于Logistic数学模型，分别从多维建模、舆情主体交互机理、舆情演化机理等角度对网络舆情进行了数学建模与演化趋势的分析预测，为网络舆情的定量研究提供了很好的研究思路。除此之外，为了深入分析舆情主体的内在属性以舆情主体间互动关系对于舆情演化的影响，广大学者又分别从微观角度与宏观角度入手提出了元胞自动机模型[9]、传染病模型[10]以及复杂网络模型[1, 11, 12](小世界网络模、无标度网络模型、意见领袖模型)等进一步深化舆情系统的相关研究。但是由于不同尺度上建模研究方法侧重点的不同，使得其在舆情主体内在属性以及舆情主体间互动能力的刻画有所差别，如微观尺度上元胞自动机模型仅适合主体与有限个体交互情况下的舆情演化研究、宏观尺度上的传染病模型仅适用于小规模群体且拓扑结构简单固定下的舆情演化研究、基于复杂网络的数学模型虽然能有效的解决上述两种数学建模的缺陷，但是该建模方法将不同的舆情主体无差别的统一为复杂网络结点后在主体内在属性上的刻画上有所欠缺。

综上所述，现有网络舆情的分析研究中，从定性视角开展的网络舆情研究，由于缺乏网络舆情传播规律的定量描述，因而难以揭示网络舆情在传播过程中的变化规律亦难以实现网络舆情的趋势预测与科学管控；基于数学建模的定量研究，通过将舆情主体类比为物理粒子或者无差别的网络节点，将现有物理系统的建模手段引入网络舆情研究后虽然取得了一定的进展，但是由于研究框架的限制，现有研究较少考虑舆情主体非物理的“社会属性”，如人特有的记忆特性、长程非线性交互等因素，使得所得数学模型难以解释实际网络舆情系统中存在的过冲现象、长尾现象。

考虑到舆情主体的记忆特性以及实际舆情系统中呈现出来的过冲、长尾现象等特征，本文拟在分数阶微积分学框架下重新考虑网络舆情的建模问题，通过提出的分数阶微分方程模型，进一步融合舆情主体的记忆特性以改进现有整数阶数学模型的缺陷，同时实现网络舆情系统的精细刻画，为舆情趋势的准确预测及其科学管控提供参考。

1 基于分数阶微积分的网络舆情系统建模

诞生于300多年前的分数阶微积分是古典微积分的进一步扩展，其本意为任意阶次的微分和积分。由如下分数阶积分(1)与分数阶微分(2)的定义

(1)

(2)

可以看出在分数阶微分的定义(2)中由于融合了卷积算子*使得在分数阶导数的定义可以方便的考虑历史信息的影响，进而弥补了整数阶微分仅仅依赖局部信息的缺陷。显而易见，分数阶微积分可以看作是经典整数阶Leibnitz微积分的延伸和拓广，整数阶Leibnitz微积分则是分数阶微积分的特殊情况。尽管分数阶微积分与整数阶微积分几乎同时出现，但由于认识的局限性，同时由于缺乏对于分数阶微积分物理、几何意义以及应用背景的解释，致使分数阶微积分自诞生后仅仅停留在数学家们的理论研究中。近年来，人们逐渐认识到分数阶微积分在描述物理世界以及各种现象方面的优势，例如在粘弹性材料或者具有内在记忆、遗传特性过程上分数阶微积分具有天然的优势；同时由于分数阶微积分方程的解析解为呈现幂律递减的Mittag-Leffler函数的组合，使得很多具有幂律特征的复杂现象或者过程都可以利用分数阶微积分方程来描述或者解释。分数阶微积分目前受到越来越多的重视与关注，己经在物理学、电化学、非线性动力学系统、机器人技术、信号处理、电气工程、控制系统以及生物工程等领域[13]表现出巨大的应用前景，成为当前国际上新兴的研究热点。

现有针对网络舆情的建模研究首先在舆情主体满足如下图1所示“刺激-反应”模式的情况下，提出了描述舆情系统演化的整数阶Logistic模型。

图1 刺激-反应模式

(3)

其中，r为某类网络舆情信息的增长率，xmax为某类网络舆情信息的最大容量或某类网络舆情交互互动后最终的稳态值，x0为舆情信息量初始值。

受整数阶导数定义所限，舆情系统(3)的演化仅考虑了局部范围内舆情信息的影响。在实际网络舆情演化中，由于记忆与社会经验等因素的制约，舆情主体对于舆情信息接收、舆情信息处理到舆情信息输出的整个过程，可以进一步用图2所示“刺激—认知—反应”模式来描述，其中认知阶段与舆情主体的早期记忆、经历、个人经验密切相关，因而可能定义在较长时间区间。

图2 刺激-认知-反应模式

考虑到分数阶数学模型在舆情主题记忆等特性刻画上存在的天然优势，本文在分数阶微积分学框架下，提出如下的分数阶Logistic数学模型，以降低现有整数阶数学模型的保守性。

(4)

其中，分数阶微积分的定义采用与(2)等价的如下Caputo定义：

注：当舆情主体自身的经历、情绪与现实世界中的突发事件产生共鸣时，就可能诱发网络群体的社会情绪，导致突发事件在网络上的广泛传播与爆发。突发事件发生后，舆情主体的外在输出表现与其早期记忆、经历、个人经验都密切相关，因而难以简单的用图1所示的“刺激-反应”模式来描述。

2 网络舆情系统的动态演化分析

2.1整数阶Logistic动力学建模针对以整数阶模型(3)为主的网络舆情系统建模，基于变量分离方法可以得到数学模型(3)如下的解析解：

可以看出，网络舆情信息量x(t)是关于时间t的一个增函数，且逐渐收敛到舆情信息量的最大值xmax。

鉴于对于大多数函数而言，分数阶微积分三种定义(GL,RL,Caputo)上的等价性，在kh，(k=1,2,…) 时刻α阶的分数阶导数可由下式描述。

其中，Lm为分数阶微分算子中记忆长度的刻画，h为所获取采样数据的间隔。基于上述微分算子的数值估计，分数阶数学模型(4)可以重新描述为：

(5)

考虑到(5)式左端可通过当下舆情数据与历史舆情数据获取，进而可以基于最小二乘的多项式拟合实现未知参数r与xmax的估计。

注：由舆情系统分数阶数学模型(5)的左端可以看出，分数阶导数的“记忆”特性使得在当下舆情演化趋势的分析过程中有效融合了舆情历史信息，整数阶数学模型(3)仅为分数阶数学模型(4)或(5)的特殊情形，因而分数阶数学模型(5)式可以更加精细、更加准确的描述舆情系统的演化趋势。

3 实例建模与应用

以央视曝光的河南知名企业双汇“瘦肉精”养猪事件为例。瘦肉精可以增加动物的瘦肉量使肉品提早上市、降低成本。但瘦肉精有较强的毒性，长期使用有可能导致染色体畸变，诱发恶性肿瘤。事情曝光后引起社会各界的广泛关注和热议，图3为采集到的16天内对于“瘦肉精”事件持有关注与批评等意见的网络舆情信息。

图3 (a) 每日舆情信息变化示意图

图3 (b) 舆情信息总量变化示意图

图4 舆情系统基于整数阶模型的趋势演化图 (α=1)

类似于前述舆情系统的整数阶数学建模研究，在分数阶导数α=1.5的情况下，可以得到r=0.2487，xmax=1130。通过图5所示趋势演化图可以看出对于舆情事件持有关注与批评态度的网络舆情仍然处在快速的上升期，并且有可能出现“过冲”现象，如有可能需要采取必要的管控措施，以促进舆情系统的健康发展。

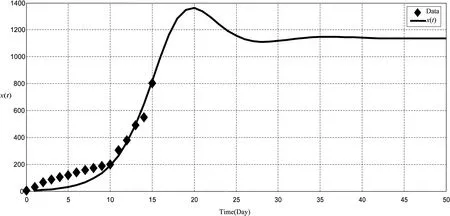
图5 舆情系统基于分数阶模型的趋势演化图 (α=1.5)

4 结 论

本文在分数阶微积分学框架下，研究了网络舆情系统的数学建模问题，通过分数阶Logistic模型与整数阶Logistic模型的建立，在舆情系统的数学建模过程中进一步考虑了历史舆情信息的影响作用，将整数阶数学模型推广到分数阶数学模型。同时通过具体的网络舆情事件，展示了分数阶微积分学在舆情趋势预测方面的优势与重要性，为后续网络舆情的科学引导与合理管控奠定了理论基础。