一种基于合作博弈论的自动驾驶车道变更模型

刘 超 丁 箐

(中国科学技术大学软件学院 安徽 合肥 230051)

0 引 言

自动驾驶[1]近年来受到越来越多的关注，而车道变更[2-4]是自动驾驶技术中最重要也是最具有挑战性的任务。违法的和危险的车道变更会引起严重的交通事故、大量的经济损失以及人口伤亡。研究安全有效的车道变更模型对于自动驾驶领域就显得尤为重要。

已有文献中车道变更模型可以分为非合作模型与合作模型两种。非合作模型主要可以分为基于规则的变道模型、基于非合作博弈的变道模型，以及其他非合作模型等。文献[5]提出了一种基于规则的变道模型，车辆通过进行一系列的判断来决定是否可以变道。由于缺乏与其他车辆的交流与合作，该模型在很多情境下并不适用。文献[6]提出了一种基于非合作博弈的模型，通过模拟人工变道过程，使用信号灯以及小步横移和周围车辆交互，进行变道。由于车辆间不进行合作，在变道过程中无法始终保持车辆之间的安全距离。文献[7]则提出了一种基于Stackelberg博弈的模型，它通过挑选具有充足车距的目标车辆来完成变道行为。文献[8]则提出了一种在互联车辆间传递信息来完成变道的非合作博弈方法。非合作车道变更模型一般是对周围环境进行分析预测来做出最大化自身收益的选择。但车辆间不进行合作就很难保证整体收益最大化，甚至在极端情况下可能无法完成变道。其他诸如基于机器学习[9]、强化学习以及马尔可夫决策模型也同样忽略了合作的重要性。

事实上，车道变更的本质就是车辆之间进行合作的结果。文献[10]认为在整个车道变更过程中，车辆之间进行合作可以极大提高车辆之间的安全性。文献[11]针对在人类监控之下的自动驾驶车辆，设计了基于社会状态和交易补偿的博弈策略来激励车辆完成合作变道行为。文献[12]设计了一个多Agent的马尔可夫博弈模型，同时使用深度强化学习来求出博弈解。作者提出了一种被动-主动合作变道框架来刻画变道过程，每一个参与车辆通过调整自己的行为来达到博弈的纳什均衡。文献[13]假设车辆想要变道时，周围车辆通过提供车距来配合它完成变道。由于车辆间不进行交互，速度可能产生大幅度变化，引起强烈的驾驶不适感。由于没有采取任何措施来激励车辆，很难保证车辆一定会参与合作。

本文首次将合作博弈理论应用到车道变更领域，提出了一种针对自动驾驶车辆的新颖的变道模型。该模型将想要变道的车辆以及它周围的车辆作为一个整体，内部的每一个参与者进行合作，以提高整体收益为目的，同时每一个参与者的个体收益也能够增加。本文首先提出了用于两车合作的纳什讨价还价博弈模型，然后扩展为三车合作博弈模型，分别求出了对应的纳什讨价还价解[17]和夏普利值[18]。在个体收益分配方案中加入了支付补偿部分实现收益的可转移性，起到激励车辆积极参与合作的作用。该模型保证了变道过程中车辆间整体安全距离得到有效的保持，车辆整体通行速度增加的同时驾驶舒适性也得到提升。

1 系统模型

假设在车道变更过程中，变道车辆与周围车辆作为一个整体，其内部车辆通过协作实现加速与减速来完成变道过程。随后这些车辆通过纳什讨价还价博弈以及三人合作博弈完成整体收益的分配。

图1为一个简单真实车道变更场景，在纳什讨价还价模型中，carA打开信号灯，想要变更车道到Lane-3，carB选择合作，创造出空间来配合carA完成变道。在三车合作博弈模型中，当carA想要变道时，carB以及carC都选择合作来完成变道过程。

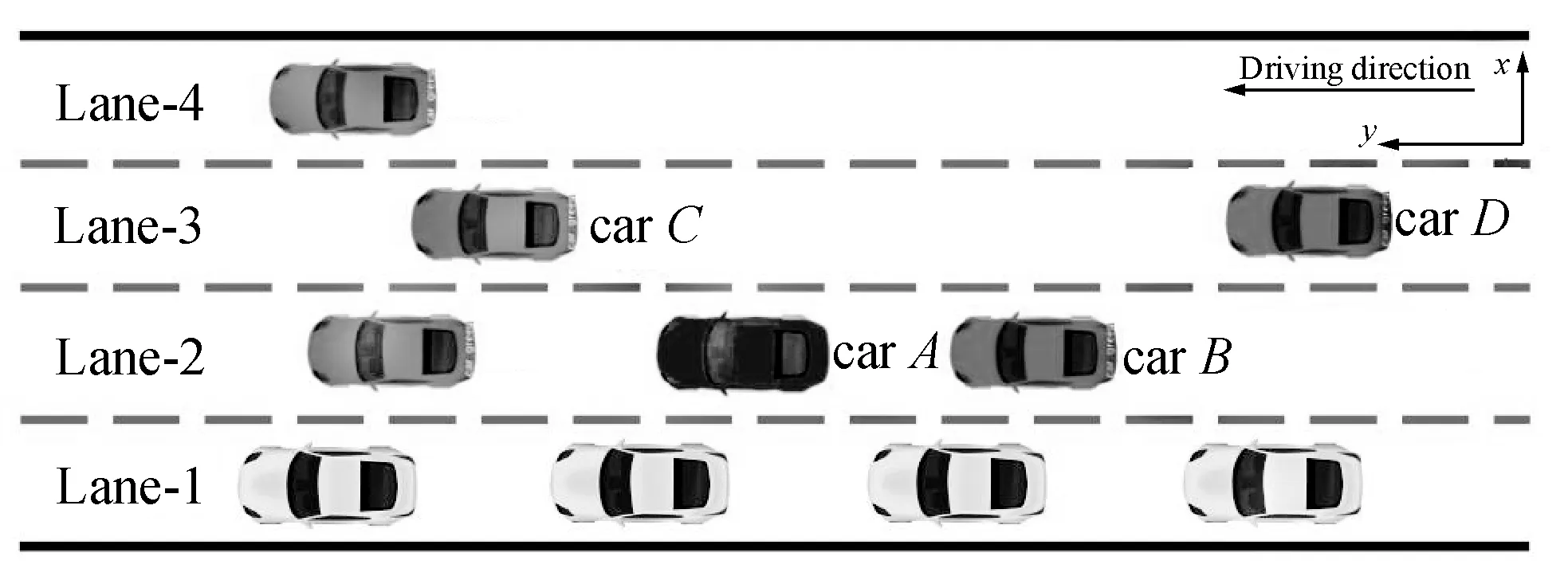
图1 车道变更问题的场景图

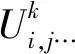
(1)

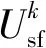
(2)

(3)

xij(t)=xi(t)-xj(j)

(4)

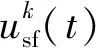
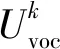
(5)

ΔVθ=Vθ(t=n)-Vθ(t=1)

(6)

(7)

(8)

式中：Wθ是carθ的舒适性收益;aθ(t)代表t时刻车辆的加速度。

2 基于合作博弈的车道变更模型

本节首先提出两车合作博弈模型，然后扩展到三车辆的合作博弈模型。

2.1 基于纳什讨价还价的车道变更模型

两人合作博弈就是纳什讨价还价博弈，假设参与者1与参与者2进行合作所获得的整体收益为u(1,2)。经过一系列协商后，参与者1所获得的个体收益为p1，参与者2为p2，同时p1+p2=u(1,2)。则(p1,p2)为整体收益的一种分配方案，所有可能的(p1,p2)组成了纳什讨价还价博弈的可行配置集合，记为F。如果双方协商不成功，合作无法达成，(u(1),u(2))就是谈判的破碎点，u(1)、u(2)即为参与者不合作时的收益。

模型中车辆整体的收益是由安全性、速度、舒适性三部分组成，如果这些收益无法在参与者间进行转移，就会导致无法达到纳什讨价还价解。于是在个体收益分配方案中加入了交易补偿部分(Upay)，使得收益可以在参与者之间进行转移。这里首先提出了一种个体收益分配方案(pA,pB)如式(9)和式(10)所示，然后证明该方案就是本轮博弈的纳什讨价还价解。

(9)

(10)

式中：Upay是car A用于激励其他车辆参与合作所支付补偿的金额。

如车辆间谈判失败，carB不进行合作，假设其会继续保持匀速行进而不减速，当两车间距离小于一定数值，carA就会取消变道操作。当车辆不进行合作时，各自的收益u(A)与u(B)分别表示为:

(11)

(12)

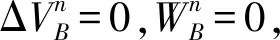
如果一个可行配置(p1,p2)(其中p1≥u(1),p2≥u(2))是该博弈的纳什讨价还价解，当且仅当存在正整数λ1>0与λ2>0，使得λ1(p1-u(1))=λ2(p2-u(2))与λ1p1+λ2p2=maxy∈F(λ1p1+λ2p2)同时成立。

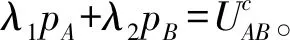
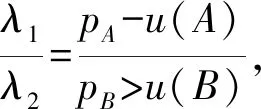
2.2 基于合作博弈的车道变更模型

在三车辆的合作博弈变道模型中，参与车辆的集合为N={A,B,C}，博弈的联盟S为N的子集，同时一共包含2n-1个非空子集。联盟S的收益函数V(S)表示为:

(13)

(14)

(15)

(16)

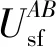
不同的联盟有着不同的整体收益，但是本例中如果联盟没有car A的参与，就不会发生车道变更行为，则整个联盟的收益为零。对于car B和car C而言，都需要car A参加联盟，那样它们才能获得更高的个体收益。但car A是选择car B或者car C或者两者组成联盟，则取决于car A在哪个联盟中的个体收益更高。

在合作博弈论中，求解的方式有很多种，夏普利值是人们普遍认同且没有歧义的求解合作博弈问题方式。式(17)使用夏普利值来求解联盟S中参与者的收益。

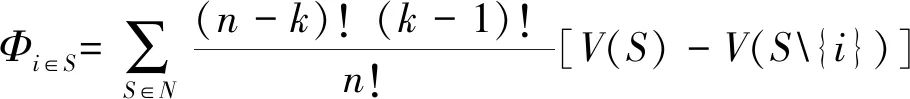
(17)

式中：k是联盟S中参与者的个数;n是大联盟N中的参与者的个数。

与上述的纳什讨价还价博弈模型一样，该博弈中的联盟的收益也是由安全性、速度以及舒适度三个方面组成，但是这些收益同样无法在参与者之间进行转移，也就无法取到相对应的夏普利值。因此在本次博弈中个体的收益分配策略中加入了交易补偿部分，来实现参与者之间收益的可转移性。大联盟中每一个个体的收益方案如下所示：

(18)

(19)

(20)

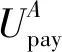
3 实验与结果分析

本文采用MATLAB/simulink仿真软件对基于纳什讨价博弈的车道变更模型以及基于合作博弈的车道变更模型进行了仿真验证。在仿真实验中的所有车辆都安装了合作变道模块，可以根据不同的场景进行合作，完成变道操作。在实验中，每一个车辆都有自己的坐标位置、速度、加速度以及初始车道等相关参数，这些参数会在不同场景下的实验中发生改变，当车辆的初始车道参数发生变化后，就意味着车道变更过程完成。我们还考虑了不同类型的车辆对我们提出模型的影响，将车辆类型分为大卡车、公交车、小汽车三种类型进行实验。与此同时，不同类型车辆的安全车距以及最小车距是不同的，大卡车的安全车距大于公交车，公交车大于小汽车。由于实验存在重复性，本文选择了其中更困难的情况来进行实验，而不考虑所有不同类型车辆的组合。实验中car A为变道车辆，它的类型包括上述三种，car B为小汽车，car C为大客车。实验目的主要有：① 验证本文提出的模型是否有效地提升了所有车辆整体的收益；② 计算每一个参与者的个体收益和car A用于激励其他车辆参与合作所需要的代价Upay。实验的相关参数如表1所示。

表1 相关参数表

表1中：VA、VB和VC分别是car A、car B和car C的初始速度，XA、XB和XC是车辆的初始位置。同时amax是car A的最大加速度，Xsf1、Xsf2以及Xd分别是car A和car B的安全车距、car A与car C的安全车距以及车辆之间的最小车距，当car A为大卡车时，amax=1 m/s2，Xsf1=15 m，Xsf2=20 m，Xd=3m；car A为公交车时，amax=1.5 m/s2，Xxf1=12 m，Xxf2=18 m，Xd=2 m；car A为小汽车时，amax=2 m/s2，Xsf1=10 m，Xsf2=15 m，Xd=1 m。同时，LA、LB、LC分别是car A、car B、car C的初始车道。

3.1 基于纳什讨价还价模型的相关实验

在本文提出的基于纳什讨价还价车道变更模型中，car A做最大加速的加速操作，直到速度达到Vmax后，保持匀速运动，同时car B进行相应的减速操作，保证车辆之间的安全车距，直到车辆之间的距离达到安全车距后，car A进行变更车道，操作完成后，车辆的车道参数发生变化。本文通过以下几个实验来仿真模拟正常交通状况的纳什讨价还价变道模型。

实验中横坐标表示car A与car B初始位置的相对距离。图2显示了在不同相对距离之下，车辆之间合作与不合作时整体收益的对比。当车辆之间的相对距离足够大时，合作与不合作对整体收益的影响很微小。但是随着相对车距的逐渐减少，合作对整体收益的影响就远远大于它们不合作的时候。同时当相对车距很小时，不进行合作是无法完成变道的，整体收益降为零。从图3可以看出，小汽车合作时获得的整体收益大于公交车和大卡车，那是因为不同类型的车辆的安全车距不同，同等情况下，大卡车和公交车的安全车距是大于小汽车的，那么整体的安全性收益就会降低，同时大卡车和公交车的速度增量没有小汽车大。

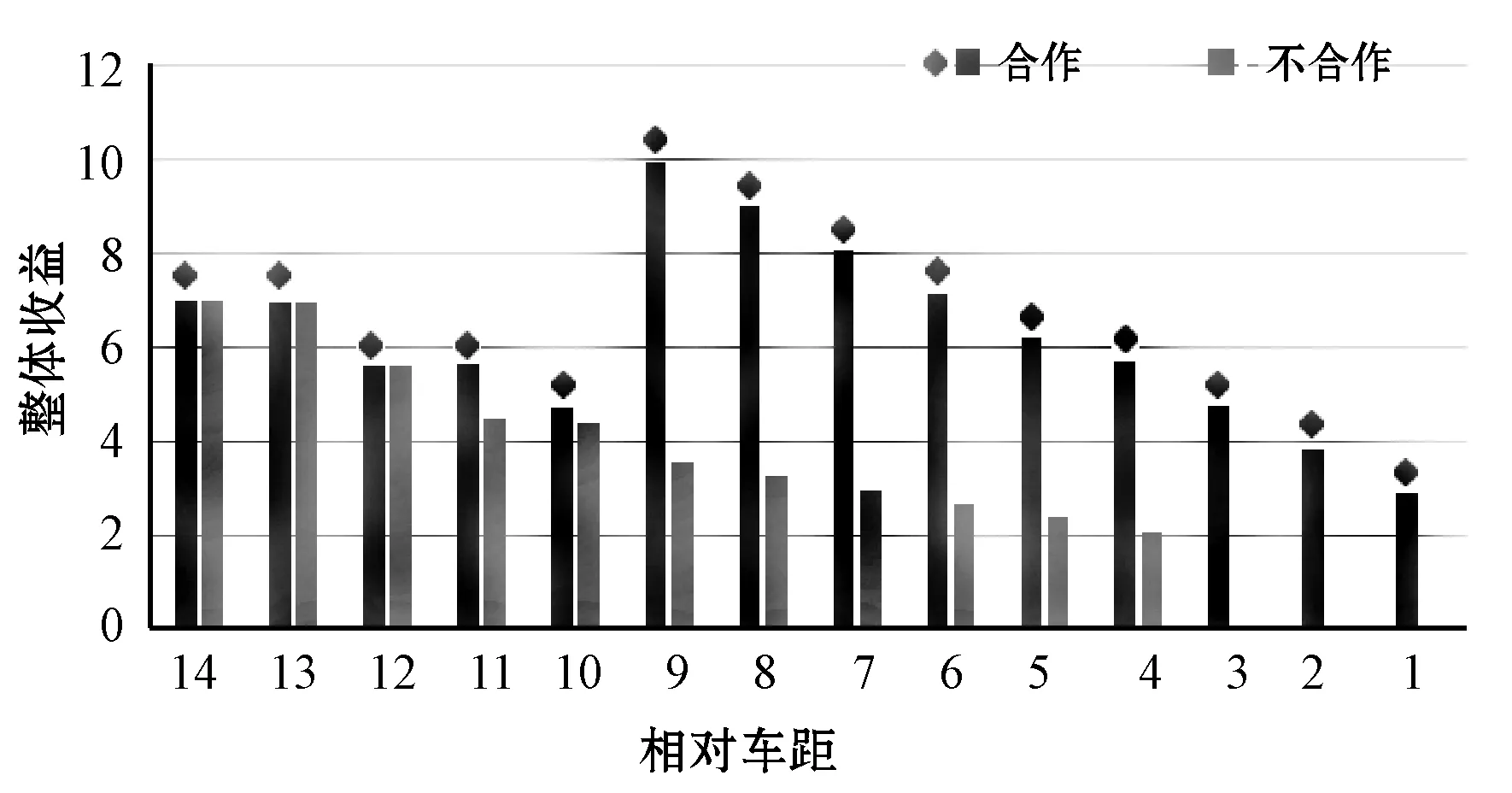
图2 合作与不合作的整体收益对比

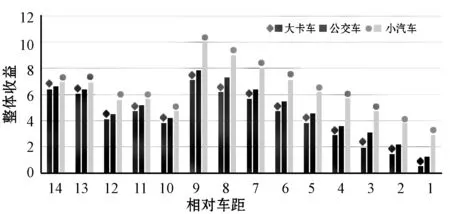
图3 不同车辆类型下的整体收益

从图4可以看出，car A的个体收益绝大多数情况是大于car B的个体收益的。当相对车距足够大时，car A基本占了所有的收益，car A用于激励car B进行合作的支付代价很小。但是随着车距的逐渐减小，需要的支付代价越来越大，那么car B的收益逐渐增加，car A的收益逐渐减小。图5中car A随着车距变小和加速度变小，支付代价变得更大。当车距越来越小时，需要支付的代价就越来越大，同时加速度越大，需要支付的代价就越小。因为在车距比较小或者加速度比较小时，更需要其他车辆的合作，所以需要更大的支付代价来激励其他车辆进行合作。

图4 个体收益

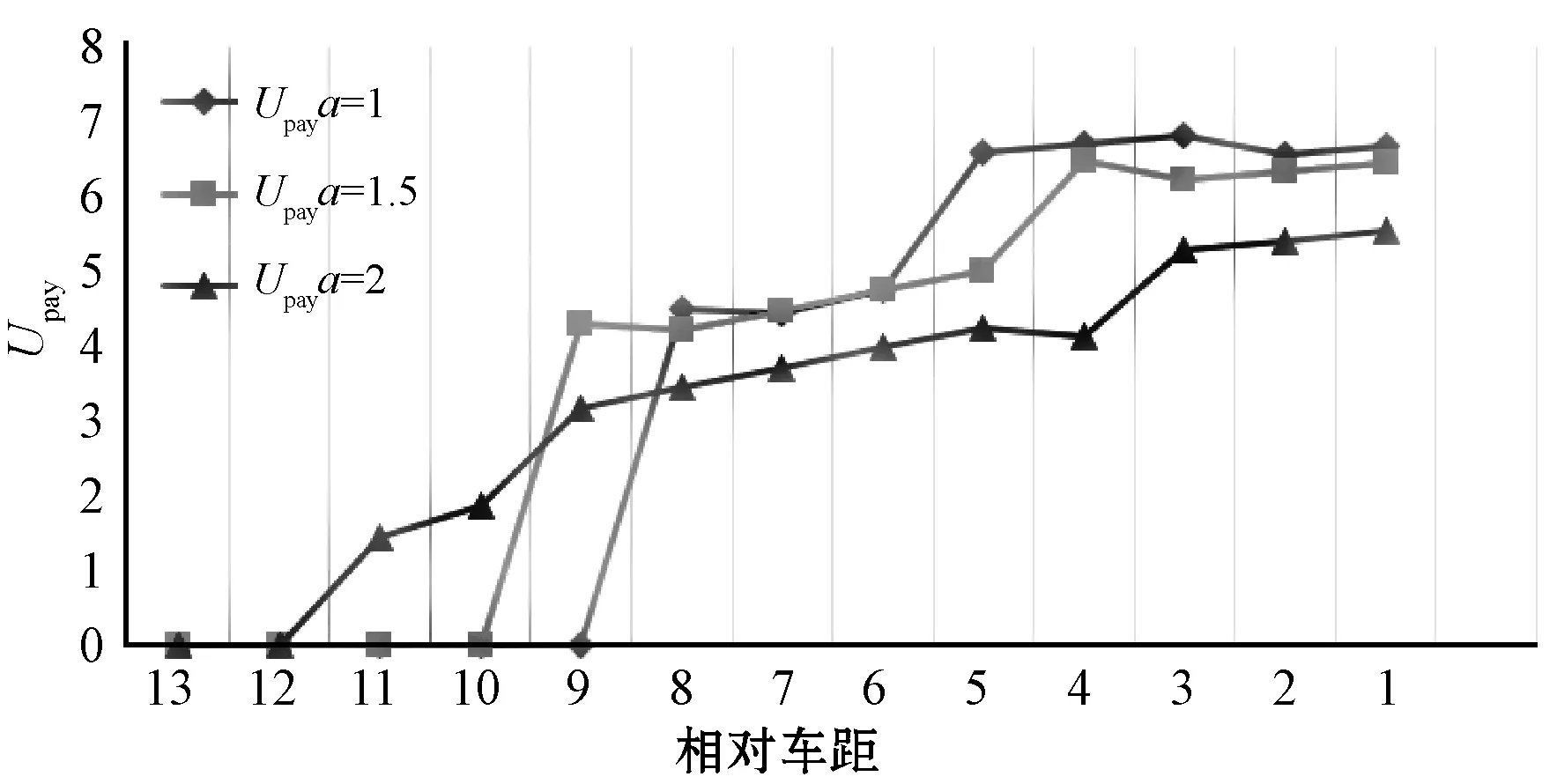
图5 不同加速度下的支付代价

3.2 基于合作博弈模型的相关实验

基于合作博弈论的模型是由二人纳什讨价还价模型加入了car C，扩展而来的三车辆合作变道模型。其中，car A和car B进行合作的操作和上述的模型是一样的，同时如果car C进行合作，那么它就会进行加速操作，保持与car A的安全车距来配合完成变道过程中。反之，则保持匀速运动。

在图6中清楚地展示了大联盟的整体收益远远高于其他联盟。主要是因为所有参与者都参与合作时，安全性收益和速度增量就会更大。图7中的实验表明了小汽车类型的大联盟整体收益大于其他类型的整体收益。那是因为其他类型车辆的安全车距大于小汽车，从而导致相应的整体的安全性收益小于小汽车类型的联盟。与此同时，小汽车的速度增量也大于其他类型，所以小汽车类型的联盟的整体收益最大。图8则显示了不同联盟之下car A的夏普利值。实验结果显示，在大联盟下的car A的夏普利值(car A的个体收益)相对于其他联盟是最大的，那么car A就会选择加入大联盟。

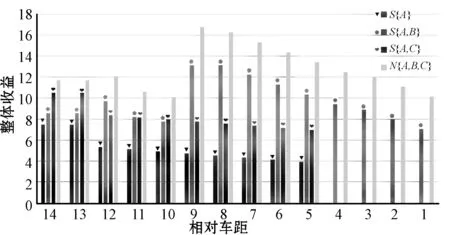
图6 不同联盟之下的整体收益

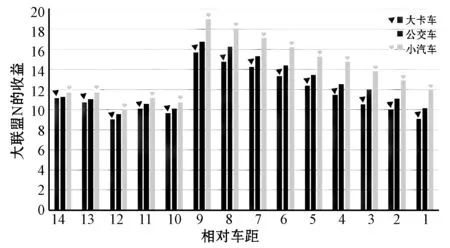
图7 不同车辆类型下大联盟的收益

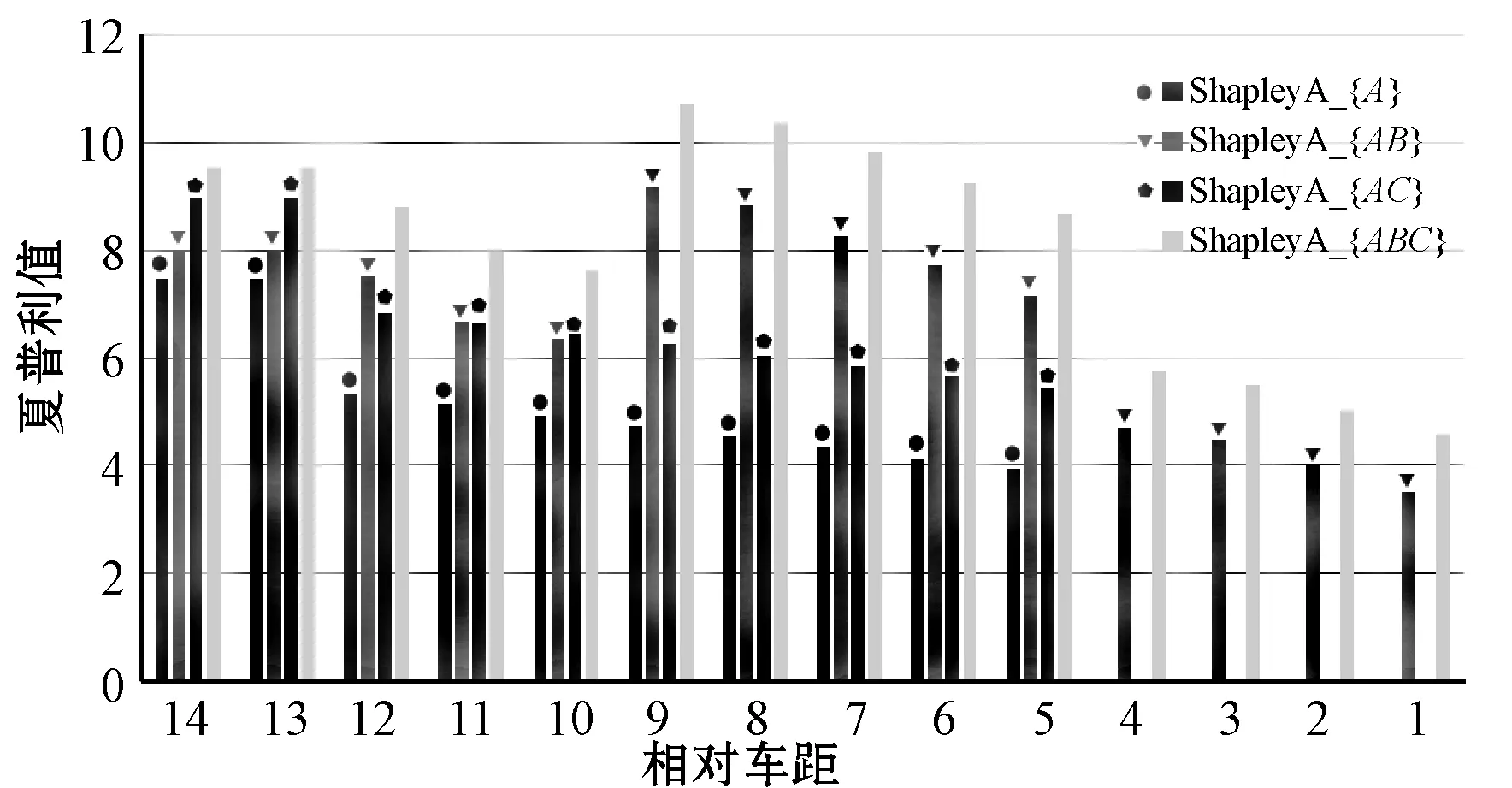
图8 不同联盟下的夏普利值

图9给出了大联盟中不同参与者的个体收益的变化趋势。当相对车距足够大时，car A对联盟的影响最大，因为只需要支付很小的代价来激励其他车辆完成变道操作，其他车辆收益相对较小。但是，随着车距不断减小，其他车辆的合作就显得尤为重要，car A想要完成变道，就需要支付更多的代价，那么它的收益降低，其他车辆的收益就会增大。图10则显示了不同车距与不同加速度之下的car A需要支付代价Upay的变化。当车距变小和加速度变小时，car A支付代价更大。因为车距越小或者加速度越小时，更需要其他车辆的合作，所以需要更大的支付代价来激励其他车辆进行合作。

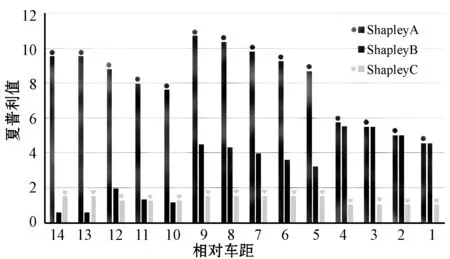
图9 大联盟下不同参与者的夏普利值

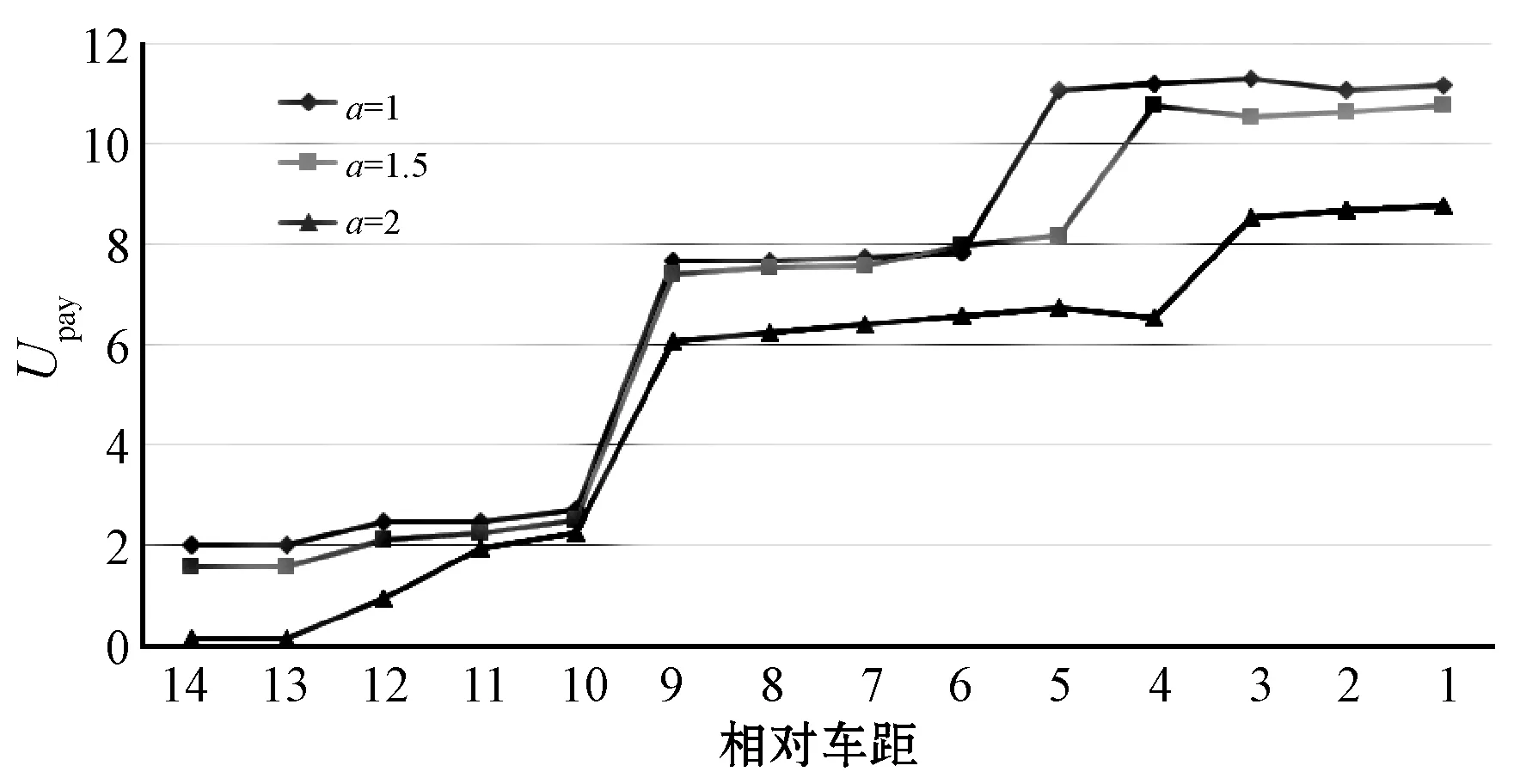
图10 大联盟下的支付代价

4 结 语

本文首次将合作博弈理论应用到车道变更领域，提出了用于两车合作的纳什讨价换博弈模型和三车合作的合作博弈模型，将想要变道的车辆以及它周围的车辆看作为一个整体，整体内部的每一个参与者进行合作，并求出了相对应的纳什讨价解和夏普利值。同时本文在个体收益分配方案中加入了支付补偿部分实现了收益的可转移性，从而可以取得相对应的解，起到了激励车辆积极参与合作的作用。实验表明，进行合作，车辆整体收益有着大幅增长，同时合作的每一个参与者的个体收益也有着明显的增加。