双重非均匀子群参数制作研究

黄 冬，袁 媛，张 乾，李 颂，梁越超

(1.西安交通大学 核科学与技术学院，陕西 西安 710049；2.中国核电工程有限公司，北京 100840；3.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001；4.海军工程大学 核科学技术学院，湖北 武汉 430033；5.国防科技大学 并行与分布处理国防科技重点实验室，湖南 长沙 410073)

弥散颗粒燃料元件中燃料颗粒弥散在非裂变基体中，该燃料元件能承受更高的温度，具有优秀的固有安全性。近年来引入压水堆的全陶瓷微密封(FCM)燃料，将燃料颗粒弥散在SiC基体中，制作为圆柱形燃料芯块[1]。这种弥散形式的燃料颗粒，难以获得确定的几何信息，同时由于共振自屏现象的存在，呈现出一种双重非均匀系统，如果不在共振计算中考虑双重性，将对中子输运计算带来不可忽视的无限增殖因数误差。

针对弥散颗粒燃料的共振计算，当前国际上主要有3种方法，分别为丹可夫方法[2]、缺陷因子法[3-6]和Sanchez-Pomraning方法[7]。这些研究倾向于沿用或改进传统压水堆组件计算程序中的共振计算方法，在几何适应性、计算精度上还存在局限性。美国橡树岭国家实验室实现了嵌入式共振计算方法在随机分布介质燃料元件中的应用[8]，但未使用考虑双重非均匀性几何的共振积分表。DeCART程序中实现了子群方法在随机分布介质燃料元件中的应用，但沿用了压水堆问题中的子群参数[9]。本研究试图提出双重非均匀系统下共振积分表和子群参数，基于Sanchez-Pomraning模型下的特征线固定源计算方法，通过超细群求解慢化方程获得共振核素的共振截面，结合特征线固定源计算获得均匀化燃料区域的标通量，从而建立一套双重非均匀积分表，通过子群方法实现随机介质燃料元件的共振计算。

1 理论模型

1.1 Sanchez-Pomraning模型应用于特征线固定源计算

Sanchez-Pomraning提出的随机输运模型将微观尺度上燃料颗粒间的碰撞概率与宏观尺度上燃料元件间的碰撞概率耦合。对于包含随机分布颗粒的材料，Sanchez-Pomraning模型定义了一种统计学上的等效宏观截面：

Σt=Σt,matrix+

(1)

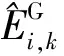
由于式(1)是关于Σt的隐式方程，通过迭代式(2)求解Σt。

(2)

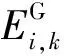
基于等效总截面，平源区的出射通量如式(3)所示，等效源项q=φasΣt，φas为渐近通量，由式(4)计算得到。

(3)

(4)

式中：φout和φin分别为出射和入射通量；L为特征线段长度；m为特征线方向索引；Smatrix和Si,k分别为基体和颗粒材料对应的源项。

通过式(3)建立传统MOC与双重非均匀系统的联系，在不含弥散颗粒的平源区，φas计算与传统MOC相同。而在弥散燃料区域，颗粒内部各层通量可通过基体通量由式(5)重构。

(5)

式中：Pik,il为第i种颗粒、第k层材料产生的中子在第l层材料发生首次碰撞的概率；Vik为颗粒i种颗粒、第k层材料的体积；q为源项。

1.2 双重非均匀共振积分表制作

通过Sanchez-Pomraning模型应用于特征线固定源计算，采用超细群慢化方程求解共振自屏截面，本文选取的超细群在共振能量段有34 000群，最终通过式(6)归并得到多群有效截面。

(6)

整个过程采用嵌入式共振计算思路实现，计算核心是针对燃料组件的实际几何，求解1个单群的固定源输运方程，由此获得燃料区域的标通量。

(7)

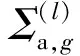
获得标通量后，通过式(8)计算出燃料颗粒的等效背景截面。

(8)

整个双重非均匀共振积分表制作流程如图1所示，主要分为如下几步。

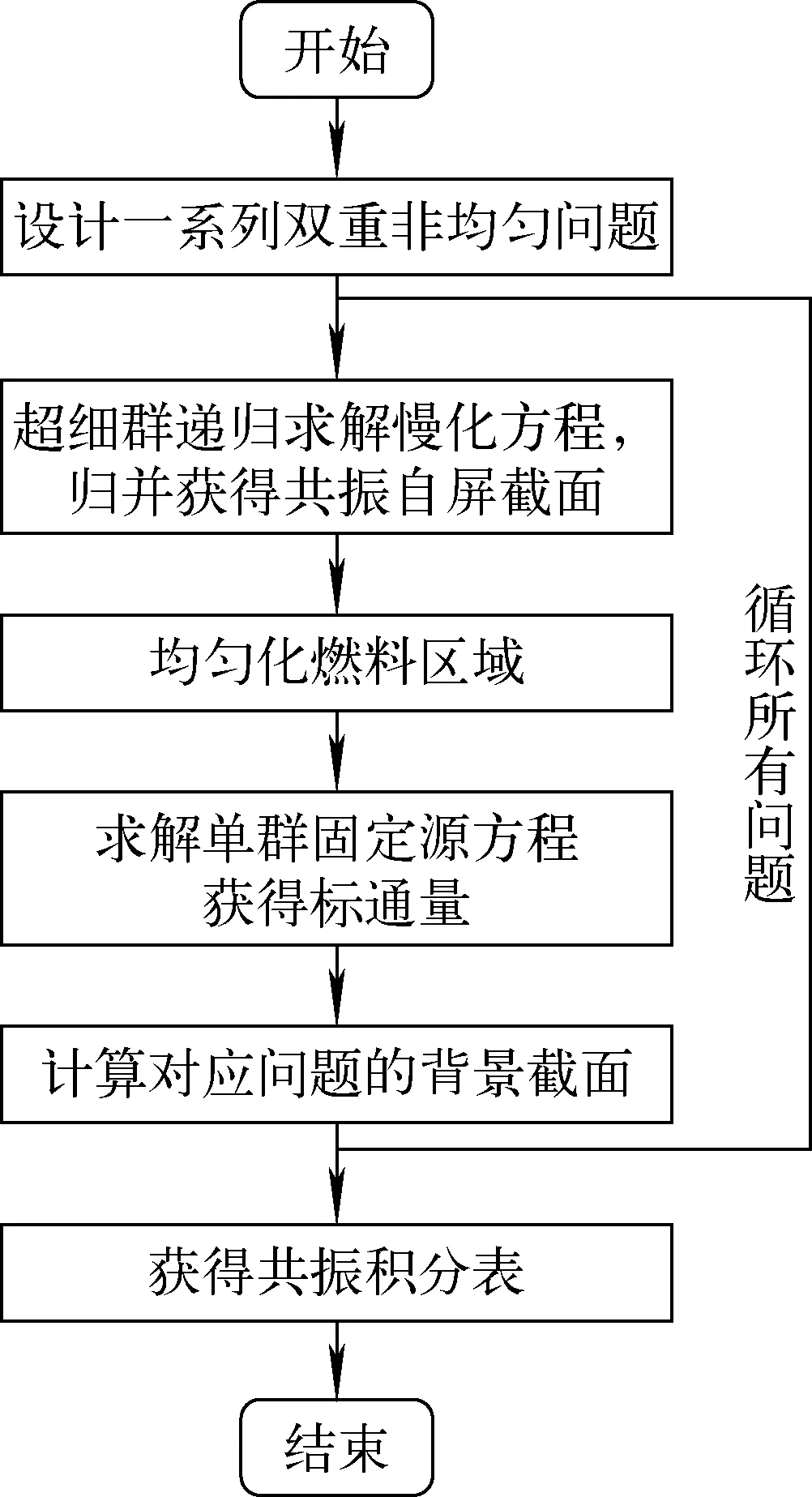
图1 双重非均匀积分表产生流程Fig.1 Generation process of double heterogeneous integral table

1) 根据目标堆型中的典型随机分布介质燃料元件，在某一温度下，改变慢化剂与弥散颗粒的燃料密度，建立一系列用于制作双重非均匀共振积分表的基础问题。

2) 对于这些基础问题，在超细群结构上，递归求解慢化方程。求解过程中，调用Sanchez-Pomraning模型固定源方程求解方法，以获得精细能群结构能谱，归并得到燃料颗粒的共振自屏截面。

3) 将弥散颗粒燃料与基体打混，燃料区域均匀化后的核子密度由式(9)得到，并用于单群固定源计算获得标通量。

(9)

4) 对于设计的所有基础问题，利用超细群求解得到的共振自屏截面，重新计算式(7)、(8)，得到每个问题对应的背景截面。

5) 每个问题的背景截面与共振自屏截面一一对应，形成双重非均匀系统下的共振积分表。

本文针对单栅元几何下的全陶瓷微胶囊封装燃料(fully ceramic microencapsulated fuel, FCM)制作了235U和238U的共振积分表，选择的温度为300 K，该栅元燃料半径0.625 2 cm,气隙半径0.633 7 cm，锆包壳半径0.690 7 cm，栅元边长1.65 cm。TRISO颗粒由内到外分为5层，分别是燃料内核、缓冲区、内层热解碳、碳化硅层、外层热解碳，其几何半径依次为0.025 0、0.034 0、0.038 0、0.041 5、0.045 5 cm。表1列出单栅元材料信息，此时燃料颗粒填充率为40%。以表1中慢化剂以及燃料密度数据为基准，设计了37个不同的双重非均匀问题列于表2。

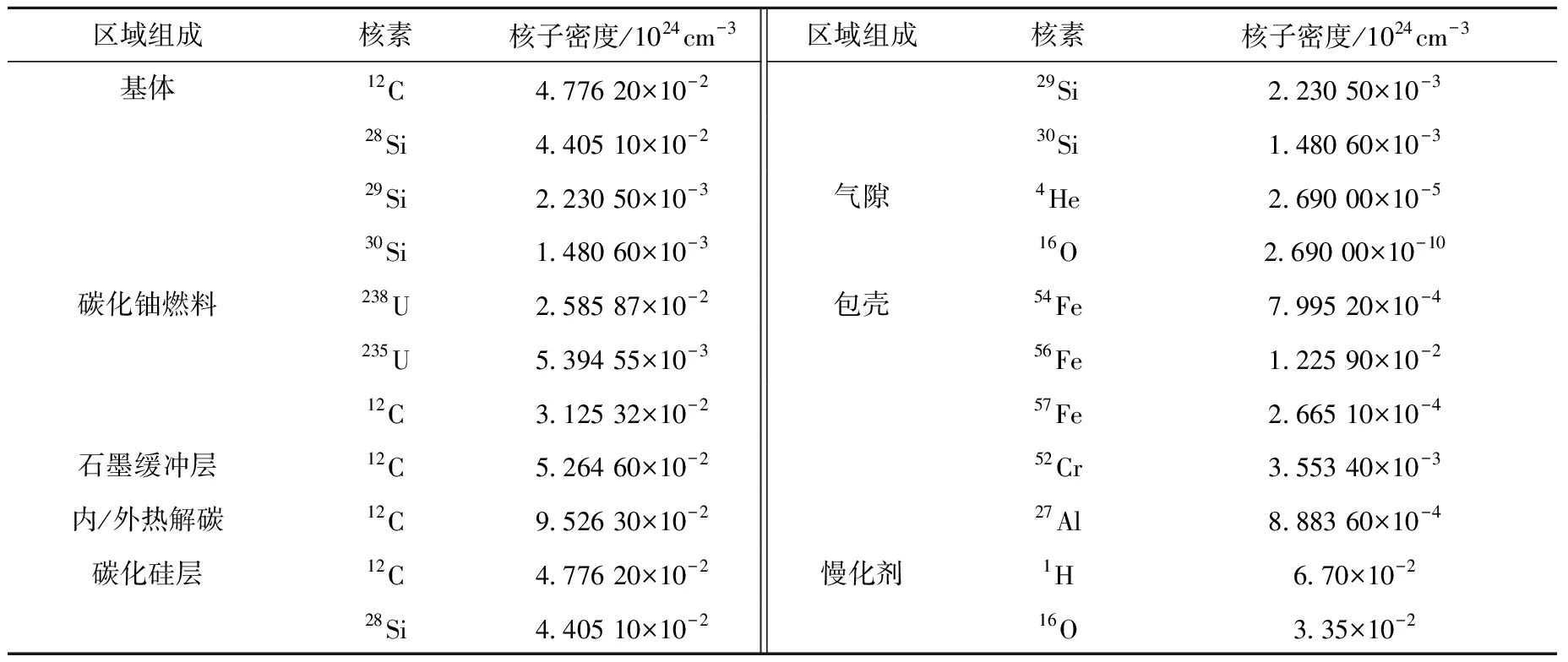
表1 FCM单栅元材料信息Table 1 FCM pin cell composition date

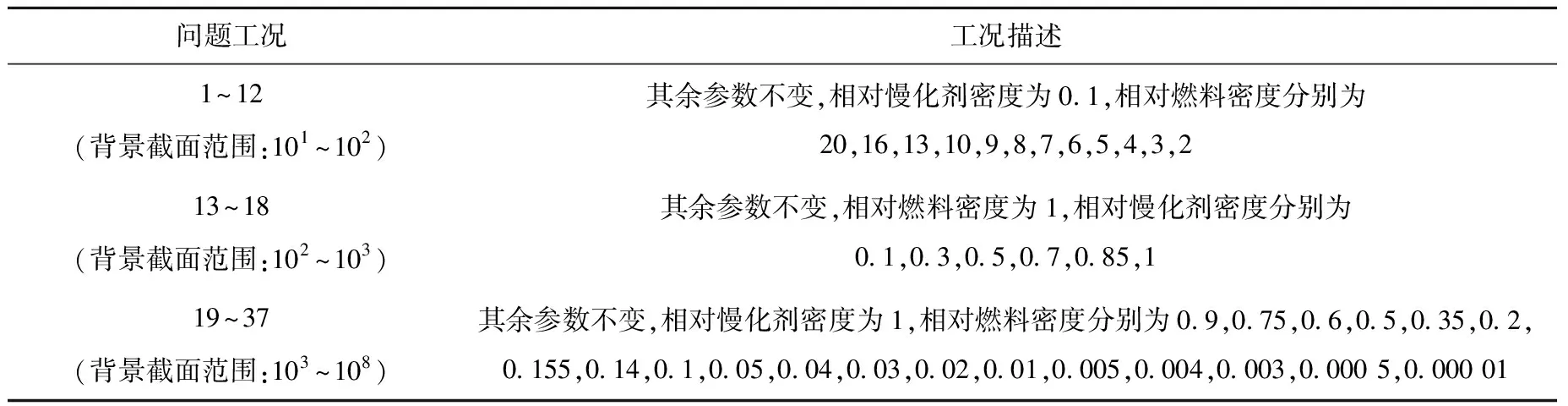
表2 双重非均匀共振积分表制作设计问题Table 2 Double heterogeneous problem used to develop resonance integral table

设计的问题尽量保证背景截面在不同数量级上都有对应的数据点。对所有设计的问题进行计算后，整合背景截面与共振截面数据，得到双重非均匀积分表。图2示出238U第10共振群(能群边界为6.476 0～6.868 0 eV)在300 K时微观吸收截面随背景截面的变化。

图2 微观吸收截面随背景截面的变化Fig.2 Microscopic absorption cross section vs. background cross section

1.3 子群参数转换

当前产生子群参数主要有拟合方法和矩方法[10-11]。拟合法直接采用有效共振积分表来拟合出子群参数，而矩方法利用真实截面的“矩”来产生子群参数，还需额外开发工具产生“矩”。本文通过拟合方法产生子群参数，获得双重非均匀共振积分表后，即可根据背景截面与共振截面联立式(10)、(11)求解子群参数。

(10)

(11)

式中：σt,sg、psg分别为第sg子群的总截面和概率；σ0,n、σt,g(σ0,n)分别为第n个背景截面和该背景截面对应的第g群总截面；N为子群数目。

获得子群总截面和子群概率后，可根据式(12)计算子群分截面。

(12)

式中：σx,n为第n子群的x分截面；x为反应类型，包括吸收、散射和裂变。

2 数值验证

本文计算使用的多群数据库版本为ENDF/B-Ⅶ，采用HELIOS-1.11程序的47群能群结构[12]，共振群能量范围为1.855～9 188 eV。选取FCM燃料单栅元问题对得到的双重非均匀子群参数(DHSP)进行验证，通过调用基于Sanchez-Pomraning方法的MOC输运模块恢复出FCM燃料的238U和235U共振截面，最后调用相同的输运模块进行本征值计算。以基于Sanchez-Pomraning方法的超细群(UFGSP)[13]求得的共振截面为基准，最后以相同的输运模块计算keff，分析由子群共振部分对keff带来的偏差，总的偏差以蒙特卡罗程序serpent[14]计算为基准。

2.1 算例描述

本文的积分表以UFGSP计算得到的截面为基准，进而转换得到子群参数。积分表在栅元尺寸1.6 cm、填充率为40%、富集度17.08%的条件下得到，验证子群参数时，对栅元尺寸、填充率和富集度进行扩展验证。算例采用的FCM燃料栅元如图3所示，其几何信息与内部填充的TRISO颗粒信息列于表3，材料信息见表1。

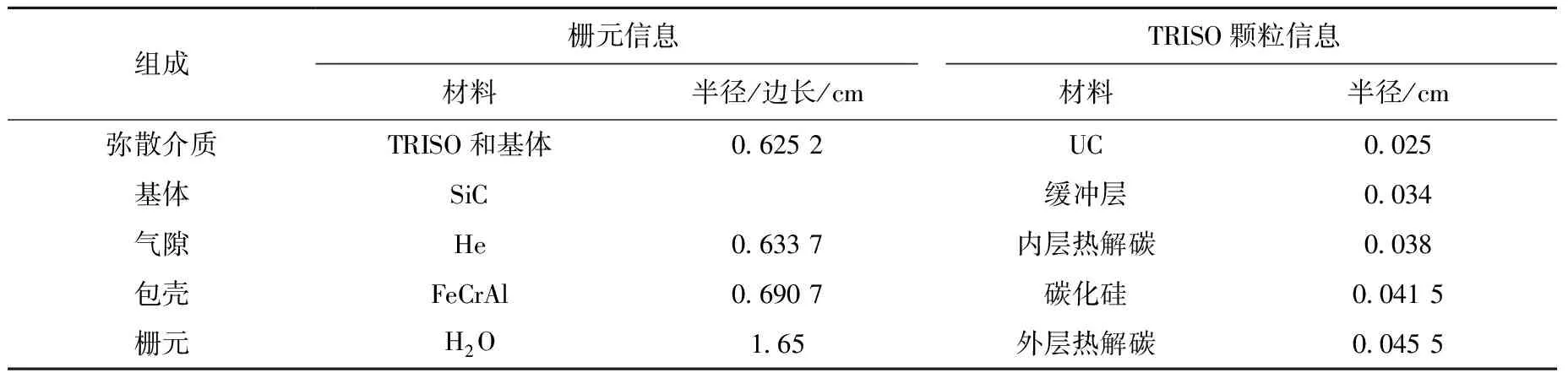
表3 FCM燃料内部材料与几何尺寸Table 3 Information of material and geometry for FCM fuel

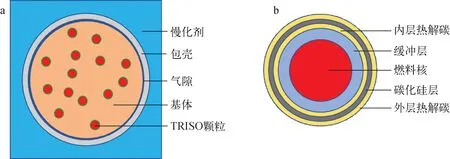
图3 FCM栅元结构(a)及TRISO颗粒(b)Fig.3 FCM cell structure (a) and TRISO particles (b)

2.2 不同栅元几何计算验证

将栅元尺寸从1.65 cm扩展到1.55～1.85 cm进行计算，DHSP与UFGSP调用相同的输运求解器，以UFGSP的截面为基准，两个结果的偏差近似认为由子群共振额外引入(表4和图4)。从表4和图4上看，共振部分偏差在100 pcm以内。238U吸收截面相对偏差为3.5%，235U吸收截面相对偏差在1%以内。

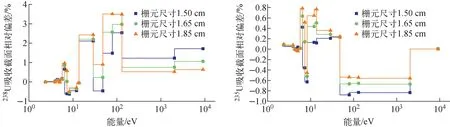
图4 不同栅元尺寸下238U和235U吸收截面相对偏差Fig.4 Relative deviation of absorption cross-section of 238U and 235U under different cell sizes

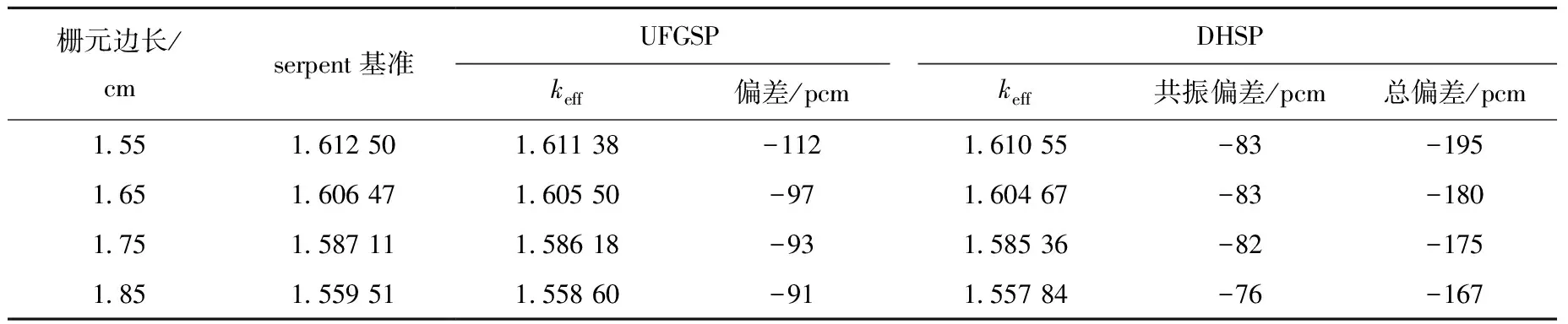
表4 不同栅元尺寸计算结果Table 4 Geometric calculation results of different pin cell sizes

2.3 不同填充率计算验证

验证不同填充率下的计算情况，本问题从制作积分表时40%的填充率扩展到35%～45%进行测试。测试问题中，栅元边长1.65 cm，富集度17.08%，其余信息与表3相同，计算结果列于表5。图5为不同填充率下238U和235U吸收截面相对偏差。

从表5和图5可知，验证结果中共振部分出现的最大绝对偏差为-149 pcm，与基准相比总偏差最大达到-205 pcm。在35%填充率时，238U吸收截面相对偏差达到了4%。由于子群参数根据积分表拟合得到，在不同背景截面范围的拟合程度存在差异，当填充率增大背景截面减小时引入的共振偏差有所降低。

表5 不同填充率下的计算结果Table 5 Calculated results of different filling rates

图5 不同填充率下238U和235U吸收截面相对偏差Fig.5 Relative deviation of absorption cross-section of 238U and 235U under different filling rates

2.4 不同富集度计算验证

改变算例富集度进行测试，从制作积分表时17.08%的富集度扩展到9%～25%进行计算。测试问题中，栅元边长1.65 cm，其余信息与表3相同，计算结果列于表6，图6示出不同富集度下238U和235U吸收截面的计算精度。

图6 不同富集度下238U和235U吸收截面相对偏差Fig.6 Relative deviation of absorption cross-section of 238U and 235U under different enrichments

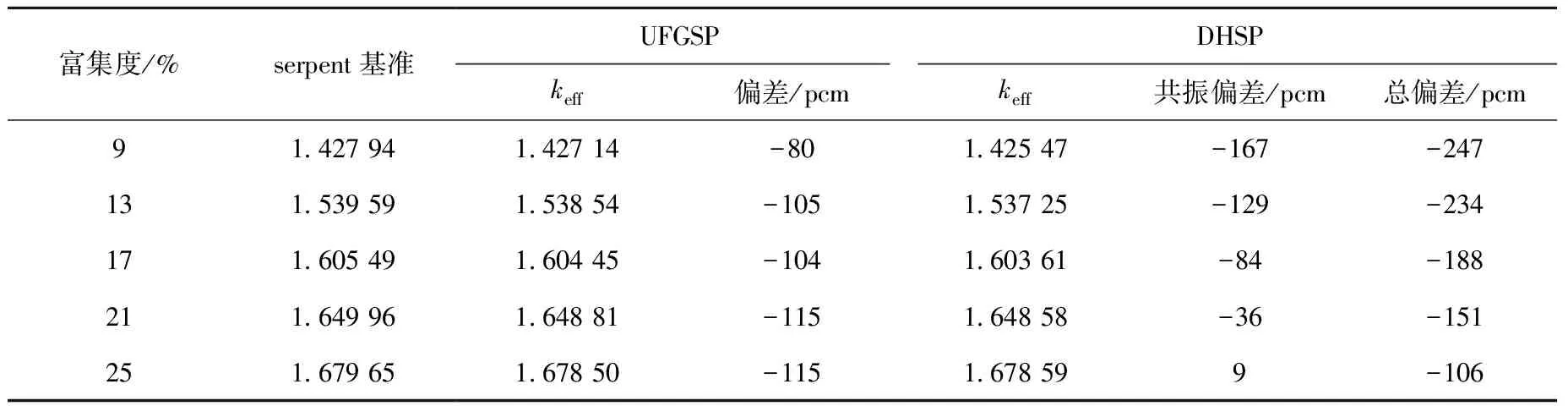
表6 不同富集度下的计算结果Table 6 Calculated results of different enrichments

可看出，富集度为9%时，子群共振引入的偏差达到-167 pcm，与蒙特卡罗的基准之间总偏差达到-247 pcm。对于截面计算，238U的吸收截面相对偏差最大达到4%，235U的吸收截面最大相对偏差也达到2%。这些情况同样是子群参数对不同背景截面段的拟合程度存在差异，验证算例的富集度变化范围较大，对应的背景截面变化稍大，由结果来看，合理推测存在某个富集度使得引入共振偏差恰好为0，偏离该富集度越远偏差越大。

2.5 燃耗问题

用于燃耗问题的子群参数在填充率30%，富集度17.08%的情况下重新获得，同样以此作为初始条件计算FCM燃料的燃耗过程，其中每个燃耗步的核子密度与有效增殖因数由serpent提供，对各燃耗步的核素组成，利用该子群参数恢复出238U与235U的共振截面，其余共振核素的截面仍由超细群计算得到。整体上看，在图7中计算的燃耗过程中，该子群参数可较好地计算FCM燃料的燃耗过程。

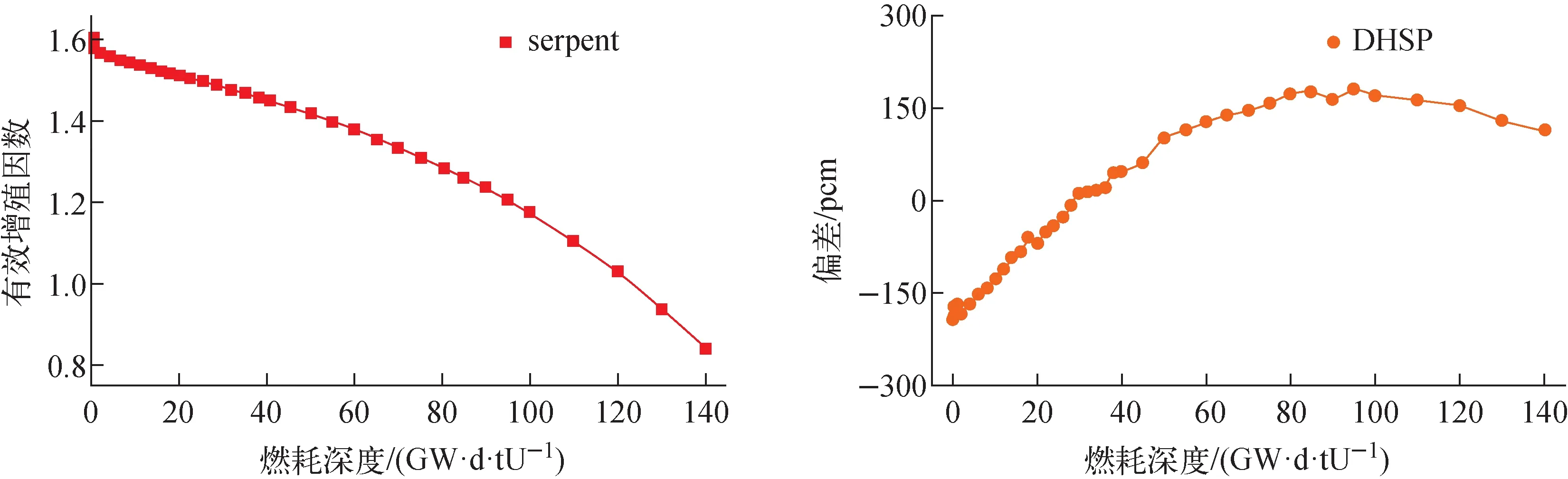
图7 燃耗过程的keff偏差Fig.7 Deviation of keff during burn-up process

3 结论与展望

针对弥散颗粒型燃料随机性及双重非均匀性问题，本文通过基于Sanchez-Pomraning的超细群方法，制作了一套耦合宏观与微观尺度的双重非均匀性共振积分表，并结合子群方法实现随机介质燃料元件共振截面的计算。数值结果表明，该套子群参数很好的延续了子群方法在几何适应性上优势，同时对于35%～45%的颗粒填充率，以及9%～25%的富集度扩展问题上仍旧有较高的计算精度。在多颗粒问题上情况变得复杂，不便于共振积分表的建立，此方法尚不适用，日后将展开研究，同时本文仅在300 K下建立了共振积分表，在更大的温度范围，以及更多种不同的工况下还需要建立额外的积分表验证测试。