大范围低压供电区电力消费及窃电规律研究

2022-01-27宋纯贺王天然

太原理工大学学报 2022年1期

陈曦，宋纯贺，王天然

(1.中国科学院网络控制系统重点实验室，沈阳 110016；2.中国科学院沈阳自动化研究所，沈阳 110016；3.中国科学院机器人与智能制造研究院，沈阳 110016；4.中国科学院大学，北京 100049)

电力系统的安全稳定运行对于保障国民经济的发展有着至关重要的作用。中国是电力大国，发电量占全球总量的25%以上[1]。过去由于电力系统拓扑结构复杂、信息化程度低，电力数据的收集成为难题，这严重阻碍了电力系统运行状态的高效分析。随着物联网和智能电网的发展，电力系统大量设备接入信息网络之中。在此基础上，电力系统运行状态数据的实时采集成为可能，为电力系统大数据分析奠定了基础。

电力系统大数据分析涉及内容广泛，如日前能耗预测[2]、电器能耗分析[3]、电力系统故障检测[4]等。本文主要针对用户用电消费特征进行分析。目前该领域的研究呈现出以下特征。首先，以往对用户用电消费情况的研究主要集中在中高压地区[5]，对城市低压地区的研究较少。高压通常指高于1 000 V的电压等级，中高压通常面向大型场所和区域，低压电是指配电线路交流电压在1 000 V以下或直流电压在1 500 V以下的电接户线，低压通常与民用相关。高压供电对象相对单一，数据获取相对容易。与高压供电相比，低压的电力数据容量更大，用电形式多样，面向对象更复杂，获取难度更高，导致相关研究较少。其次，因为实时线损数据很难获取，对于线损率的数据挖掘也比较少，以往的研究主要集中在计算理论线损率上，而且多为中高压的地区。如王守祥等[6]提出的统计线损方法。

基于国家电网公司的大规模实测数据，本文研究了220 V、380 V供电电压区居民用户的用电消费特征。相对于以往中高压区域研究，以及基于仿真的电力系统线损和窃电识别，本文的研究更具有实际意义。本文的贡献可以总结为：

1) 对正常用户和窃电用户的用电时间序列数据进行了对比分析，发现窃电用户用电周期是正常用户的2倍。周期可以作为初步排查窃电用户的手段。

2) 分析了窃电用户与台区线损率之间的关系，发现台区线损率大于40%时窃电用户数量显著增加。可以优先检测此部分台区内的窃电用户来快速排查。

3) 提出了基于时间序列相似度度量和k-means聚类相结合的聚类模型得到6类台区线损率模式，并基于核密度估计对比了不同模式的分布差别，可以快速排查出重点检测台区并监测线损率改善的情况。

1 数据预处理与技术路线

1.1 数据集的来源

电力系统对安全性要求很高，导致电力数据保密性强，开放程度低。本文使用的电力数据来源于国家电网公司，原始数据集共分4个部分，由于该数据涉及保密，数据集进行脱敏处理，部分参数仅为代码表示。

1.1.1用户档案数据集

第一部分数据为用电的档案数据。数据集包含111 160个用户，每个用户拥有9个标签数据，包括用户编号，立户日期，合同容量，用户状态，用户类别，电压等级，用电类别，行类类别，台区编号，这些数据的字段代码在表1中给出。其中，台区是指(一台)变压器的供电范围或区域[7]；合同容量指供电部门许可并在供用电合同中的用户受电设备总容量，也称认可容量[8]；用户类型共有两种，包括家庭用电和商业用电；电压等级有两种，包括220 V和380 V；用电类别共有10种，由于数据保密性，已经进行了脱敏处理，由数字代替；行业类别共有228种，同样进行了脱敏处理，由数字代替。

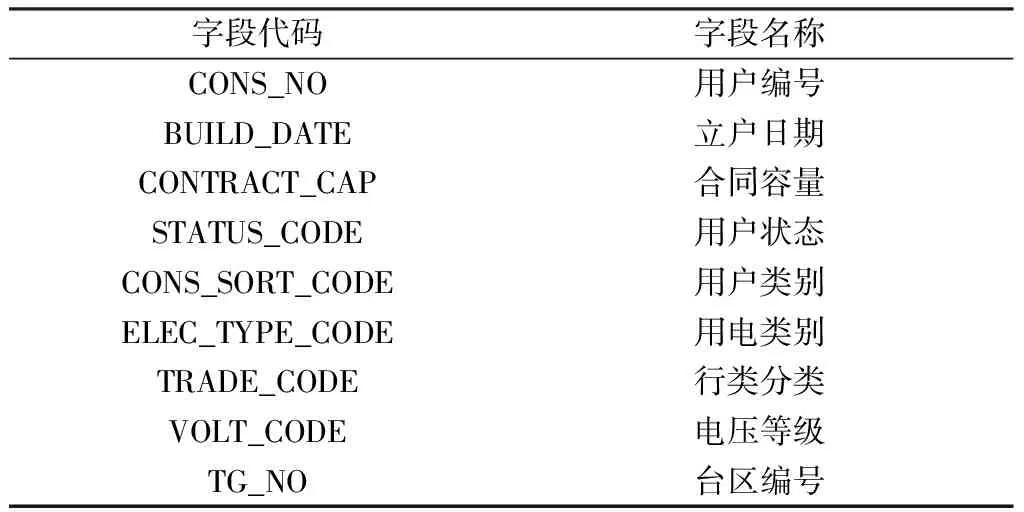
表1 用户档案数据集Table 1 Consumer profile data set

1.1.2用户用电量数据集

数据集中共包含99 999个用户，时间从2014年1月1日到2017年3月21日的用电量数据，拥有81 802 066行的数据，2.3 G的容量。数据的参数包括：用户编号，日期，当天电能表示值，用电量，对应的字段代码和数据类型在表2中给出。用户日用电量记录所有用户每日用电量以及当天和前一天的电能表示值。

表2 用户用电量数据Table 2 Electricity consumption data set

1.1.3标签数据集

此标签数据包含两个数据集，其中一个是已确认为窃电的用户清单，这个清单中拥有452个用户。测试集中是一些怀疑窃电但是还没有确定的需要测试的用户，此部分包含40 655个用户，其余用户是清白用户。一个用户用一个用户编号(CONS_NO)表示。

表3 标签数据Table 3 Label data set

1.1.4台区供用电量数据集

此数据集共涉及566个台区，时间从2016年6月1日到2017年6月4日，一共200 659行数据。数据集内的字段名称和字段代码如表4所示。对数据进行预处理，将时间跨度缩减为从2016年6月1日到2017年5月31日为完整的一年，对于数据缺失值进行插补。

表4 台区供用电量数据Table 4 Power supply and consumption data set of station area

台区电量损耗=台区供电量-台区用电量。造成电量损耗的原因主要由线路和设备的损耗(技术性损耗)和用户窃电(非技术性损耗)[9]构成。

基于该数据集可以计算出线损率。线损率(line loss rate，RLL)指电力网络中损耗的电能(线路损失负荷)占向电力网络供应电能(供电负荷)的百分数[10]。它由台区供电量和台区用电量计算，如公式(1)所示：

(1)

式中：RLL,d为台区的每日线损率；Sd为台区的每日供电量；Cd为台区的每日用电量。

综合线损率在行业管理配电线损标准和农网改造之后的配电线损率标准380/220 V供电下为12%[11]，因此本文将线损率大于等于12%标记为线损率异常值，高于这个值的台区是可能存在窃电的台区。

1.2 数据的预处理

数据集中的原始数据存在数据重复、数据缺失等问题，需要在电力数据分析前先对数据进行预处理，使数据符合规范和要求。对于本文中的数据，采用的数据预处理方法主要包括电力数据清洗、电力数据变换和电力数据标准化。

数据清洗主要是进行两个方面的数据处理，重复数据和缺失数据的预处理。

1) 对于重复性的数据，先将数据集中查询到的重复记录插入到一个临时数据集中，通过比较原数据表和重复记录表，再对其进行删除。对于此部分的预处理主要应用到台区供用电量数据集和用户用电量这两个部分。

2) 当缺失数据较少和缺失数据比例较低时，采用直接删除相应样本和取均值来代替缺失值的方法。在本文中，数据集由于用户用电量数据量很大，拥有几千万行，因此对于此部分数据集，主要采用对缺失数据进行直接删除的方法。对于删除以后数据量不足的用电用户进行剔除。对于台区供/用电量数据集，部分采用了取均值来代替缺失值的方法。

3) 当缺失数据较多时，对缺失数据进行插补。本文规定缺失值超过6%，此部分数据即为无意义，需进行剔除。缺失值在6%以内，通过平滑修正法进行插补，计算公式如下：

(2)

式中：Δt1和ΔT1分别表示前向采集开始和截止的时间序列的节点数目；Δt2和ΔT2分别表示后向采集开始和截止的时间序列的节点数目。

1.3 总体技术路线

本文的分析总体技术路线如图1所示。由数据采集，数据处理、分析与挖掘，知识发现和可视化4大部分组成，分别结合本文中提出的数据集和各模块方法组成总体框架。

图1 基于数据挖掘的用电规律研究的总体路线Fig.1 General line of research content

2 用电规律的综合统计模型

本文从供电、用电、线损、窃电4个方面的数据进行挖掘，通过特征提取与数据清洗，然后建立统计模型，对数据进行知识探索和可视化，组成统计模型的总体流程框架，如图2所示。

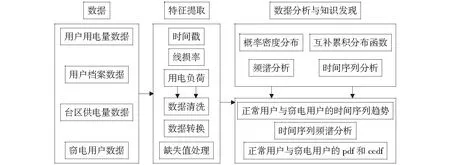
图2 用电规律的综合统计模型Fig.2 Comprehensive statistical model of electricity consumption law

2.1 用户电力消费的时间序列分析

首先对原有的101 536个用户用电量的数据进行预处理。由于数据量比较大，部分用户的数据不完整，本文将数据缺失和电力使用异常的用户剔除。筛选标准为：首先去掉重复行，将采样时间不是从2014年1月开始的用户数据全部剔除，日均用电量低于0.01 kW·h的剔除，日用电量低于0.1 kW·h数据所含比例高于50%的剔除，这部分比例基本是0值的所含比例，考虑到正常用户全年不用电的时间应该不会低于50%，留下具有较为完整数据的用户为4万左右。

首先计算这些用户的日平均用电量，然后选取全年用电量无异常无窃电的用户。为了找出正常组，本文分析了566个台区在2016年6月1日到2017年5月31日的供电量和用电量，得出了它们的线损率。在分析过程中，发现在566个台区中，以12%为标准[10]，99.82%的台区都存在窃电，平均线损率达到22.18%.从2万个数据最为完整的精选用户里筛选出线损率最无异常台区的用户，共计选择出738个用户，称为选定用户。这组用户是确定无窃电的，计算这些用户的日平均用电量。之后，将已知窃电用户的数据集整理出来，涉及452个用户，计算这些用户的日平均用电量，进行时间序列分析。窃电用户的数量较少，时间跨度完整的时间线少于正常用户，为了不影响时间序列的波动完整性，正常用户和窃电用户的时间范围没有修正为统一范围。为了对比整体用户、无窃电用户和窃电用户的用电区别，本文刻画了4万用户、选定台区用户和已知窃电用户的日用电量的时间序列，如图3所示。为了便于观察，缩放到月制度，图3中y轴是每个月份的日均用电量，x轴为时间。

从图3可以看到，不同时间序列的曲线都具有明显的周期性特征。为了探究他们的周期的详细参数以便探究不同用户日均用电量周期性的不同，本文加入了频谱分析。频谱是指一个时域在频域下的表示方式，频谱分析是针对时间序列的周期进行检测的经典方法，它简单迅速应用范围广。频谱分析将时间序列进行快速傅立叶变换(FFT)，然后将其幅频进行平方再除以时间序列的长度N：

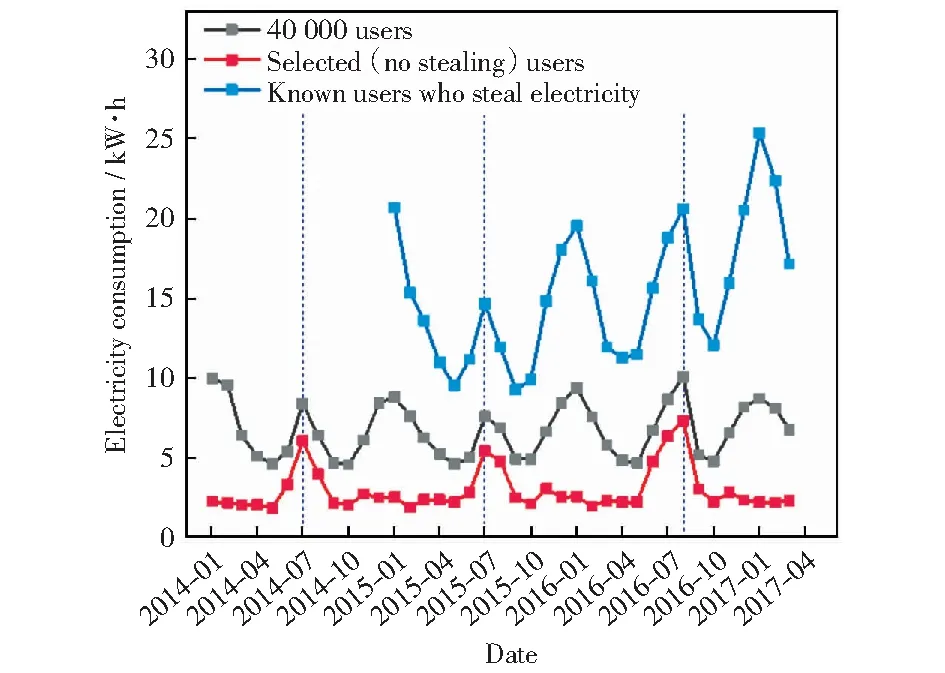
图3 4万用户、选定台区(无窃电)用户和已知窃电用户的日均用量的时间序列Fig.3 Time series of the average daily consumption of 40 000 users, selected users (without electric stealing) and known electric stealing users

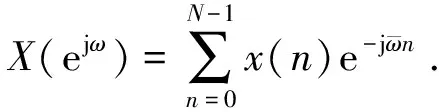
(3)

(4)

序列周期可由公式(5)获得：

(5)

频谱分析的周期图和计算周期的的结果如图4所示。其中图4(a)为数据清洗出的4万名用户的日均用电量，其中包括未确定是否窃电的用户，图4(b)为选定台区的用户，确定无窃电的区域，图4(c)为确定存在窃电行为的用户。3幅图中红虚线标出了最大谱密度所在的频率位置，序列周期结果如表5所示。

由图3、图4和表5中可以得出以下结论：

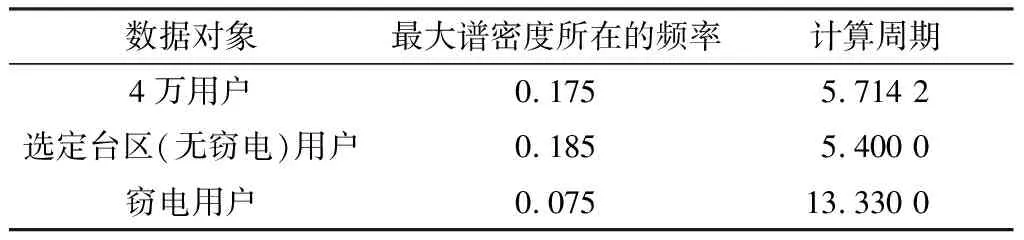
表5 频谱分析结果Table 5 Spectral analysis result

图4 4万用户、选定台区(无窃电)用户和已知窃电用户的日均用电量的时间序列的频谱分析Fig.4 Spectral analysis of time series of the average daily consumption of 40 000 users, selecited users (without electric stealing) know electric stealing users

1) 对4万总体用户，窃电用户和选定台区用户进行时间序列对比，发现均具有周期性。这个结果说明无论是否存在窃电行为，都不影响用电消费行为存在周期性规律。

2) 对4万总体用户，选定台区用户和窃电用户进行时间序列的频谱分析结果对比，发现他们的周期分别为5.714 2个月，5.4个月，13.3个月。这个结果说明正常用户和窃电用户的用电消费模型都存在周期性规律但是周期不同。

3) 每日用电量窃电用户>总体用户>正常用户。总体每日用电量不会超过26 kW·h电。这个结果说明窃电用户的用电需求比普通用户更大，但也有上限。

2.2 正常用户与窃电用户对比分析

为了进一步探究窃电用户和正常用户的不同，本文对窃电用户和正常用户分布刻画了概率密度分布曲线(probability density function)[11]也叫概率密度模型，简称pdf，如图5所示。随机变量x的取值落在某个区域的概率为概率密度函数在这个区域上的积分。对于连续随机变量x，当序列的累积分布函数是FX(x)时，非负可积函数fX(x)满足：

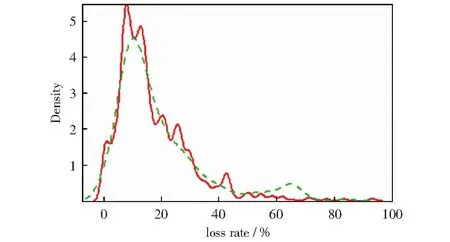
绿色虚线为窃电用户图5 正常用户与窃电用户的所在台区的数量的概率密度分布模型Fig.5 Probability density distribution curve of normal users and users who steal electricity

(6)

则fX(x)称为概率密度函数。从图5中可以看到，正常用户和窃电用户所在台区的线损率范围大部分落在了10%到20%之间。窃电用户在40%～75%的线损率异常值区间有个小的波峰突起。说明在这个区间的线损率的密度分布比较高，更容易造成窃电聚集。

为了进一步探索，绘制了互补累积分布曲线(cumulative complementary distribution function，CCDF)[12]。CCDF曲线是一个互补累积分布函数，是累积分布函数的互补，它是连续函数对所有大于a的值的概率之和，如公式(7)所示：

F(a)=P(x>a) .

(7)

其中，x为随机变量。结果如图中的图6所示。图6分别展示了3万用户和窃电用户CCDF曲线，插图是将范围缩小到0.4～0.95之间的CCDF曲线放大图。

插图是将范围缩小到0.4～1的互补累积分布曲线(CCDF)图6 正常用户与窃电用户的所在台区的互补累积分布曲线(CCDF)Fig.6 Complementary cumulative distribution curve (CCDF) of the station area where normal users and electric stealing users are located

从图6中可以看到，线损率的值达到40%时，窃电用户的CCDF比正常用户的曲线突然下降变缓，在65%左右又基本重合，说明了窃电用户在线损率范围为40%～65%数量异常，窃电用户在台区线损率大于40%时窃电用户数量激增。跟前面的概率密度分布结果相近。此部分研究证明线损率高的台区内的窃电用户数量更多，同时在实际排查窃电用户时，可以针对实时线损率40%～65%的台区进行优先检测以便来更快速地查找到窃电用户。

3 基于多用户的时间序列相似性度量的聚类

对于正常用户和窃电用户的研究中，得出线损率高的台区窃电用户会更多，但是线损率的均值并不能代表一个台区的线损损失程度，而时间序列的波动是更为准确的表达。为了更快速地从数量很多的台区里判断查找窃电用户的优先级，识别到最不健康的区域，对566个台区的时间序列曲线进行了聚类，并且为了不影响波动趋势，本文以天为维度进行聚类。

以线损率的时间序列为基础，数据包含台区在2016年6月1日到2017年5月31日的供电量、用电量数据，通过公式得到每天的线损率。每个台区具有365 d的线损率值，也是就365维度。通过时间点的直接聚类维度过高会影响聚类效果和算法实现的时间，k-means聚类简单迅速但是欧氏距离无法对时间序列相似性做出最精准的判别，时间序列相似性度量的方法可以很容易地检测两个时间序列之间的相似性，但是计算上百个时间序列时耗时过长，因此本文提出了通过时间序列相似性度量和k-means聚类相结合的方法来对566个台区的369维的时间序列进行聚类。将k-means聚类的欧氏距离进行替换来改进算法。

DTW(dynamic time warping)是广泛使用的序列数据相似性度量方法，具有相移、缩放失真和其他形状的不变性。但是DTW计算复杂度高，使得DTW难以处理高维度海量时序数据。本文提出了将基于形状的距离相关性应用于高维时间序列数据，使用SBD(shape-based distance)来衡量相似性。对于两个长度都为m的时间序列x和y，s是偏移的校正系数，s的内积公式定义如下式(8)所示：

(8)

对于所有可能的移位s范围为[m+1,m-1]，可以计算内积NCC作为时间序列x和y之间具有的相似性。NCC的最大值，表示x和y在最优偏移s处的相似性。因此，相似性度量可以克服相移和表示两个时间序列之间的形状相似性。在实践中，通常使用标准化版本的NCC限制在[-1,1]范围内，其中1表示完全相似度，-1表示两个时间序列是完全相反。NCC的定义如式(9)所示:

(9)

根据NCC定义基于形状的距离(DSB)如式(10)表示:

(10)

DSB范围从0到2，其中0表示两个时间序列具有完全相同的形状。较小的DSB意味着较高的形状相似性。

基于上述提出的相似性的度量，本文将k-means聚类[13-15]的欧式距离替换为DSB，其中k-means聚类的数目由误差平方和与轮廓系数相结合的方法求出。

将数据分成n组独立的数据样本，使n组聚类之间的方差相等，即用局部平方误差和局部最小值表示。系统为每个集群选择一个初始集群中心。每对样本xa和xb之间的距离是用DSB来表示。根据最小距离原则，将样本集分配给最近的聚类，然后用每个聚类的DSB更新聚类中心。重复上述步骤，直到集群中心不再改变。输出最终的聚类中心和k个聚类划分。采用误差平方和与轮廓系数相结合的方法选择聚类数。误差平方和为：

(11)

式中：E为度量聚类质量的目标函数，值越小越好；xi是空间中的一个点，表示样本对象；k是聚类的个数；cj是聚类的中心序列。中心序列由DSB得出：

(12)

将样本i的轮廓系数定义为:

(13)

式中：S(i)为定义样本i的轮廓系数，通过最大化均值S(i)来确定最优的簇数。本文取误差平方和较小、轮廓系数较大的k值作为最佳聚类数目。最佳类数为5-7类，由于线损率具有实际意义，从10%、20%、30%、40%甚至到100%具有不同个意义，因此将聚类数设置为6类，结果如图7所示，将566个台区的时间序列聚集成6个分类，图中是这6类的聚类中心。

从图7中可以看到不同类别的聚类中心有明确的区分。由此得到了6种台区线损率波动模式。Cluster1(1类)的线损率长期很高，根据特点将其称为大病区。Cluster2(2类)的线损率长期较高，但比Cluster1数值小，故称之为小病区。Cluster3(3类)在2016年线损率较高，在2017年线损率迅速下降，将其称之为改变区。Cluster4(4类)的线损率比标准值略高，称之为亚健康区。Cluster5(5类)的线损率长期处在标准值以内，将其称之为健康区。Cluster 6(6类)是线损率长期值超低甚至为负的过饱和区。健康区属于合格区域，其他区域属于不合格区。行业管理配电线损标准和农网改造之后的配电线损率标准为10 kV线损标准是10%，380/220 V线损标准是12%.因此本文将12%作为衡量变压器区域是否健康的标准标记在了图中。

图7 基于线损率时间序列波动的聚类中心曲线Fig.7 Time series volatility clustering center curve based on line loss rate

基于核密度估计本文将6类核密度分布做了对比。文中的核密度估计(kernel density estimation，KDE)是基于高斯核的核密度估计方法来估计单因素观测时的带宽，这种方法能够更好地观测像浏览量和用户消费的分布。通过变量x的n个观测值来计算它的概率分布[16]如式(14)所示。

(14)

其中，h是平滑的带宽，参数K是需要指定的平滑核函数。使用平滑核的标准偏差来度量核。由于误差符合独立同分布，且样本量较大，总体符合高斯分布，因此本文中使用高斯核来估计核密度：

(15)

选定了核之后，最终使用的核密度估计公式为：

(16)

分类后的用电消费和供电消费的6种类别的核密度分布的结果如图8中展示。其中图8(a)是台区用电量消费的核密度分布，图8(b)是6类在同一坐标下的用电量消费的核密度分布，图8(c)是台区供电量消耗的核密度分布。

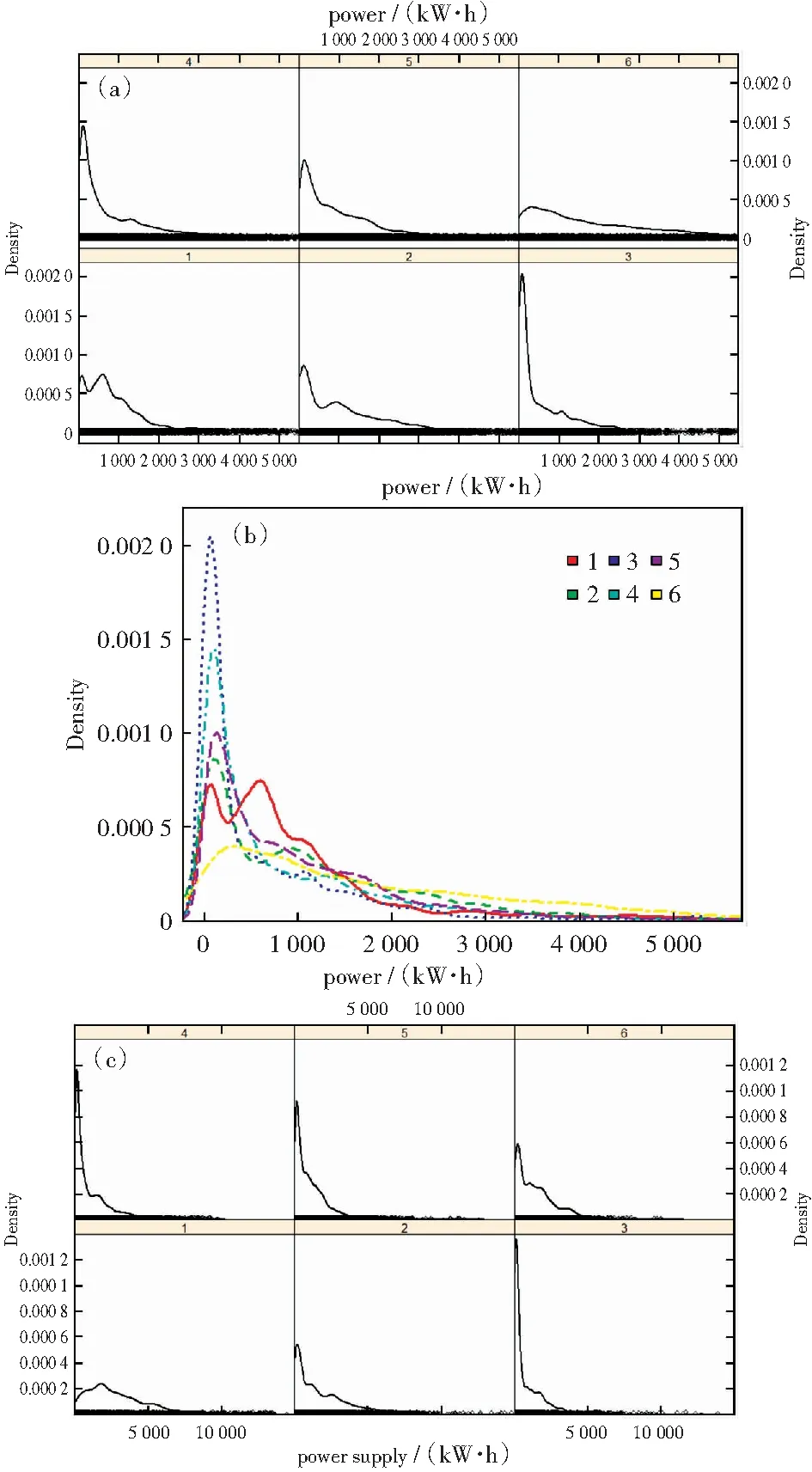
图8 用电消费和供电消费的核密度估计Fig.8 Kernel density estimation of electricity consumption and power consumption

从图8中可以看到6个类别之间明显的差异，首先从图8(a)的用电消费可以看到，6个类别各不相同，3类、4类、5类分布较为集中，是线损率较低的比较健康的区域，他们在1类2类的不健康区域数据分布比较分散。尤其是1类，它属于线损率超高的区域，它的分布有2个波峰，表明它除了正常的用电量台区外，还有一部分用电量偏高的台区在运作。2类作为第二不健康的区域，第2个波峰比较小，表明用电量偏高台区有但不是很多。第3区是线损率改善的区域，它的波峰比较高，证明它在波峰附近的数据比较集中。第6个分类过饱和区是用电量非常饱和的区域，它的分布比较饱满。为了更便于对比他们的不同，将6类用电消费的核密度分布展示在同一坐标如图8(b)所示，图中看出除了第6类的饱和区外，其他区域的第1个波峰位置是比较接近的。从图8(c)的供电分布图可以看到，供电和用电不同，它受用户窃电等原因的干扰比较小，因此3类，4类，5类，6类的分布都比较接近，2类和1类也没有2个突起，只有一个波峰。而这2类的用电量分布却有2个波峰，与这2类中含有一定的窃电用户有关。从供电和用电的对比可以看出，1类不健康区的第2个波峰才是主峰，它的峰值远远大于其他分区。因此1类模式内的台区是优先重点检测的窃电台区，其次是2类，3类是线损率改善台区，可以检测线损率改善的原因。