简而不凡的数学课堂

贾帅

摘要

教师作为学习的组织者、参与者，面对不同的数学课型，一定要转换教学观念，把学生作为课堂的主人，利用简明的设计、简练的提问、简洁的题目，主动构建简而不凡的数学课堂，引导学生不断思考，培養学生的自主学习能力。

关键词

初中数学 课堂教学 简练 简洁

“数学是一种思想，它的特点在于它的简洁与和谐。它把最复杂的东西用最简单的语言来表示，而且表达的过程是那样的赏心悦目，那样的让人神往，简直是人间最美的艺术。”简而不凡的数学课堂需要教师对一些典型问题或某个素材深度挖掘，找出内在的学习线索，科学合理地组织学生开展数学活动，从而完成多维教学目标。这样的课堂不是简简单单的数学课堂，而是经过不断思考、打磨、精练的，需要用简明的设计、简练的提问、简洁的题目引导学生思考，是真正训练思维的不凡课堂。

一、简明的设计

笔者认为，一节好的数学课，其教学设计应是简明的。教师要设计简单有效的教学活动，以实践为抓手，将教学内容的本质呈现出来，让每个学生都能参与进来，并在数学活动中自主探索和思考。下面，笔者以“反比例函数复习”为例，谈谈简明的教学设计。

教学片段：

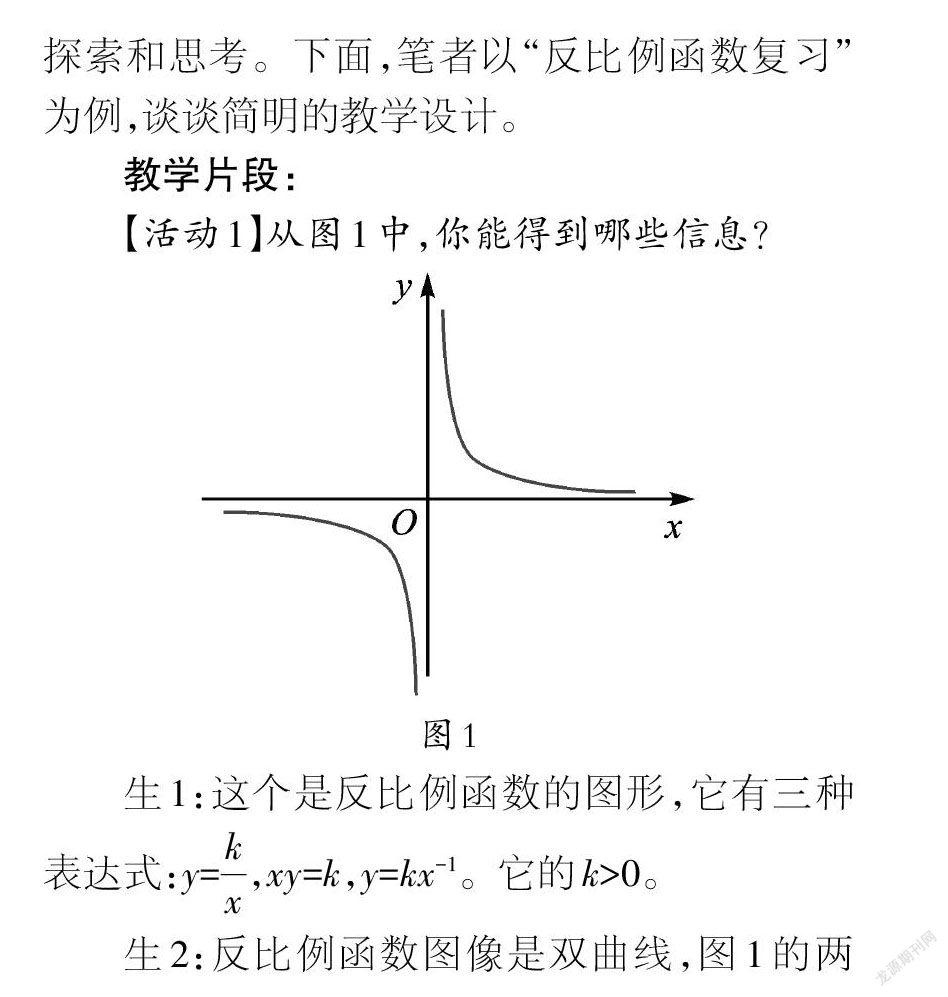
【活动1】从图1中，你能得到哪些信息？

生1：这个是反比例函数的图形，它有三种表达式：y=[kx]，xy=k，y=kx-1。它的k>0。

生2：反比例函数图像是双曲线，图1的两支，一支在第一象限，一支在第三象限。

生3：两支曲线关于原点对称，在每个象限中，y随x的增大而减小，函数图像无限接近x轴、y轴，但不相交。

生4：当k<0时，反比例函数图像在第二、四象限，两支曲线关于原点对称。在每个象限中，y随x的增大而增大，函数图像无限接近x轴、y轴，但不相交。

师：哪位同学能说一说，为什么描述反比例函数的增减性时要加“在某个象限内”？

生5：因为反比例函数的自变量x≠0。

【活动2】（1）如图2，若曲线经过点A（1，2），你能提出什么问题？

生6：我提出的问题是，该反比例函数的表达式是什么？我们可以用待定系数法，设函数表达式为y=[kx]，因为点A（1，2）在反比例函数上，所以2=[k1]，k=2，故y=[2x]。

生7：我提出的问题是，当x[≥]1时，求y的取值范围。我们可以过点（1，0）作一条直线垂直于x轴，当x[≥]1时，y的值是不断减小的，但大于0，所以0<y≤2。

生8：我提出的问题是，若y<2，求x的取值范围。我们可以过点（0，2）作一条直线垂直于y轴，当y<2时，从第一象限的图像来看，x[>]1，从第三象限来看，y的值都是小于2的，所以x<0。综上所述，x的取值范围是x<0或x[>]1。我还发现，过点A作x、y轴的垂线，与x轴、y轴围成的长方形面积为2。

师：如果我们不知道k的值，长方形的面积是多少？

生8：k的绝对值。

师：大家提出的问题都很好，也很好地解决了。现在，大家看一看老师给出的问题。若点A（x1，y1），B（x2，y2），C（x3，y3）在反比例函数图像上且x1<0<x2<x3，求y1，y2，y3的大小关系。

生9：可以用特殊值法，也可以根据图像来看，得出y2>y3>0>y1。

（2）如图3，作直线AO，交另一支曲线于点B，你又能得到哪些信息？

生10：可以求出过点A和点B的正比例函数表达式。设y=kx，因为点A（1，2）在正比例函数图像上，所以2=k∙1，解得k=2，故y=2x。也可以求出点B的坐标，把y=2x和y=[2x]联立，得出x=1或-1，因为点B在第三象限，所以点B的坐标为（-1，-2）。

师：还有其他办法求出B点的坐标吗？

生11：也可以利用反比例函数图像的对称性，A点和B点关于原点对称，所以B点坐标为（-1，-2）。

师：还能提出其他问题吗？

生12：我的问题是，什么时候反比例函数的值大于正比例函数的值？我们可以作辅助线，在第一象限内，反比例函数在正比例函数的上方时，0<x<1;在第三象限内，反比例函数在正比例函数的上方时，x<-1。所以0<x<1或x<-1。

师：还有其他想法吗？

生12：我们可以再添加一条直线，这样我们可以得到更多信息，也可以提出更多问题。

（3）如图4，再作一条过原点的直线y=[12]x，分别交双曲线于点C、D（点C在第一象限），你还能得出什么结论？

生13：可以求出点C、D的坐标。把y=[12]x和y=[2x]联立，得x=2或-2。所以点C、D的坐标分别为（2，1）和（-2，-1）。

生14：可以求出经过A、C两点的一次函数的表达式。设一次函数表达式为y=kx+b，将A（1，2）、C（2，1）代入，得y=-x+3。还可以求出其图像与x轴和y轴的交点。分别令x=0和y=0，可以得到点I的坐标为（3，0），点K的坐标为（0，3）。

生15：还可以求出△OAC的面积，S△OAC=S△OAI-S△OCI=3-[32]=[32]。

师：还有其他方法吗？

生16：可以过点A作直线l1与x轴平行，与y轴相交于点G，过点C做直线l2与y轴平行，与x轴相交与点F，l1与l2交于点H。S△OAC=S正方形OFHG-S△OAG-S△OCF-S△HAC。

生17：还可以用S△OAC=S△OCK-S△OAK这个思路去算;也可以过点C作平行于x轴的辅助线，把△OAC分成两块面积去算;还可以过A点作平行于y轴的辅助线，把△OAC分成两块面积去算。

本节课中，虽然整体来看有若干幅图，但是从数学的本质上看其实就一幅图。我们在一幅图上不断地添加一些条件，去重新认识反比例函数的性质，使得整个教学设计简洁明了，但是每幅图上所包含的信息和結论都是值得学生不断地动脑发掘、思考的。

二、简练的提问

课堂提问是组织教学的中心环节。有效的课堂提问不仅能启发和推动学生思维，提高课堂教学效率，而且对加强师生情感交流、开启学生心灵、增长学生的智力、培养学生思维品质具有十分重要的作用。数学课堂提问应该具有鼓励性、启发性、本质性，这也是“不凡”的数学课堂所追求的。

教学片段：

【问】根据篮球比赛规则，赢一场得2分，输一场得1分。在中学生篮球联赛中，某球队赛了12场，共得20分，该球队赢了几场？输了几场？

这道题笔者给了学生两分钟的思考时间。

师：大家准备怎么解决这个问题？

生1：首先要审题，找出已知量和未知量。这里的已知量是赢一场得2分，输一场得1分，总共赛了12场，共得20分。未知量是该球队赢了几场，输了几场。

师：很好，接下来怎么办？

生1：找等量关系，关键句是“总共赛了12场，共得20分”，可以设赢了x场，输了y场，根据等量关系，列出方程组[x+y=12，2x+y=20。]

师：他刚才的回答非常棒，思路很清晰，用了我们最近学习的二元一次方程组的知识解决了这个问题，还有没有其他的方法？

生2：可以用我们学习过的一元一次方程来解决这个问题。设该球队赢了x场，则输了（12-x）场，可得一元一次方程2x+（12-x）=20。

师：你能把它解出来吗？给你一分钟的时间。

生2：解得x=8。

师：如果我们把列的方程组和一元一次方程放在一起，它们有什么区别和联系？

生3：它们都可以来解决实际问题。用二元一次方程组表示数量关系更简单。一个含有2个未知数，一个含有1个未知数，含有2个未知数的我不会解，但是含有1个未知数的我会解。

师：也就是说，只有一个未知数，你就能把方程解出来了。观察两个方程的结构特点，你能不能把二元一次方程组转化为一元一次方程？

生3：二元一次方程组中2x+y=20和一元一次方程2x+（12-x）=20很相似，唯一不同的是，一个是y，另一个是（12-x）。哦！我明白了，方程组的y可以用（12-x）替换，因为方程组中还有一个方程x+y=12，可以做适当的变形，得到y=12-x。这样再代入2x+y=20中，就可以解了。

师：你的想法很好，你刚才的思路中包含着我们解方程组的重要思想——消元思想。我们一起来按照这个思路解一解这个方程组。

在这里，笔者用了6个提问和学生互动。学生开始不会解二元一次方程组，但经过与一元一次方程的对比，掌握了代入消元法的精髓，做到了从不会到会，从“无序”到“有序”。这6个提问中，有些是鼓励性的提问，有些是启发性的提问，有些是本质性的提问，这些提问都是简练的提问。在学生思考遇到困难时，教师给予适当的提示，能不断引发学生思考，帮助学生解决问题，训练学生的思维。

三、简洁的题目

简而不凡的数学课堂上，题目不应该是复杂的，而应具有代表性和更深刻的思维性。它要能够引发学生思考和交流，让学生积累数学的基本活动经验，体会数学基本思想，发展学生的数学学科素养。

教学片段：

【问】如图5，已知△ABC，求证∠A+∠B+∠C=180[°]。

师：大家怎么证明？（教室里很安静。）

师：能不能从左边的式子考虑，实现角的相加？

生1：可以作平行线对角进行迁移，我在七年级下学期的时候就学过。

师：从等式右边的180[°]，你能想到什么？

生2：两直线平行，同旁内角互补，平角为180[°]。

师：还有吗？

生3：周角的一半，两个直角相加。

师：结合左边式子和右边的结果，你能再想一想怎么证明吗？哪位同学来说一说自己的想法。

生4：先过点A作辅助线与BC平行，然后用平行线的性质就能实现角的移动，再根据平角的定义，就能得到∠B+∠BAC+∠C=180[°]。

师：好，还有其他做法吗？

生：……

总之，笔者认为，简而不凡的数学课堂，起点、立意要高，教学内容要放至整个数学系统中定位，放至初中数学内容中看作用，放至相关内容中看联系和区别。数学的教学活动是师生积极参与、交往互动、共同发展的过程。对于不同的数学课型，教师作为学习的组织者、参与者，要理解学生，以低视角、低姿态的方式教学，多鼓励，多提问，给学生充分的思考时间，帮助学生理解数学研究的基本思路。同时，教师还应转换教学观念，把学生作为课堂的主人，主动构建简约、和谐的数学课堂，引导学生在探索中发现问题，提出问题，分析问题，解决问题，以此培养学生的自主学习能力，让学生不仅会学习，而且热爱学习。

（作者单位：江苏省南京市伯乐中学）