基于二自由度预测模型的软扭矩控制方式

刘志臻，芮晖

（1．天水天传电气工程有限责任公司，甘肃 天水 741000；2．中国石油集团渤海钻探工程有限公司，河北 廓坊 065007）

在石油钻井工艺领域中，会面临钻杆负荷较大、承受压力不均衡、运动规律复杂、不同形式的振动等问题，尤其粘滑振动对钻柱会瞬间产生倍数增长的转速。这不仅会对钻井效率产生极大影响而且无法保证钻井的安全运行，设备的实际扭矩超过极限会导致卡钻、断钻现象的发生[1]。实际钻井过程中，超时会出现粘滑现象[2]，其本质就是一种无规则的非线性振动，为了消除这种振动许多学者在模型建立和钻杆控制的问题方面进行了大量研究。基于鲁棒性的二自由度（2DOF）PI控制方法[3]应用于集成受控过程，通过强制闭环函数尽可能地接近非振动的动态目标，实现平滑的性能调节；六自由度集成模型[4]根据配置轴向对称钻柱和扭转波动振动性质，提出扭转校正控制方式；通过分析粘摩擦振动的原因，动态钻柱模型利用钻柱上部角速度、钻头扭矩和重量来进行控制[5]；钻柱传动系统数学模型[6]依靠提高钻柱系统自身阻尼的控制策略，有效抑制粘滑振动，提升钻柱稳定性；五自由度的扭矩控制策略[7]采用 Riemann－Liouville 与 Oustaloup相结合的方法构成FOPID控制策略，表明该方法构建的数学模型优于其他模型。目前，国内外在钻柱动力学技术上的差距，主要集中于动力学分析软件和钻柱井下实时监测方面。

从以上研究可知，钻柱运动数学模型构建方法很多，而且都是停留在理论层面，对于钻井现场复杂的情况，并不能够完全考虑。尤其是对定向井、水平井、＞6000m井理论研究不全面。另外，还存在以下方面的问题：井下参数难以检测；数学模型难以建立导致角速度等难以精确得到；各类控制算法需要改进和完善。针对上述问题之一，本文所提出建立数学模型的方法能够很好地减少复杂运算过程，而且得到的角速度更加准确，缩短了后续控制方法的时间、增加了控制准确度。

1 建立钻柱扭转模型

钻柱振动主要分为横向、纵向、扭矩向振动。钻柱的横向振动发生在钻柱底部，由于钻具的受力不均匀，导致钻柱偏离质心，造成周期偏心转动。纵向振动一般是因为井底情况的复杂性引起钻柱伸缩振动。扭矩向振动指钻柱围绕中心线旋转，根据摩擦力的不同使得钻柱顶部与底部的旋转速度不同，从而导致扭矩向的振动产生[8]。引起粘滑振动的原因很多，如顶驱变速箱齿轮磨损产生啮合冲击、井壁间的摩擦具有随机性、受力不平衡等。

在这种非线性振动中，简化实际工况，将实际钻井工艺抽象为转盘、钻杆、钻铤和钻头。假设：当忽略底部钻具变形程度时，将钻杆、钻铤近似抽象为弹簧，保持转盘速度不变的同时，忽略井液及泥浆的阻力。因此，可以利用电动机驱动的扭摆模型来分析振动规律。钻头的转速与岩石间的干摩擦力是连续非线性变化的，K表示钻杆的刚性系数，C表示阻尼系数，转盘和钻头分别有一个粘性阻尼力矩，而且钻头还具有额外的干摩擦力矩。钻头底部的干摩擦力矩Tfd与角度ωd之间有一定的函数关系，采用库伦摩擦力结合Stribeck曲线模型近似模拟干摩擦的特性图，如图1所示。

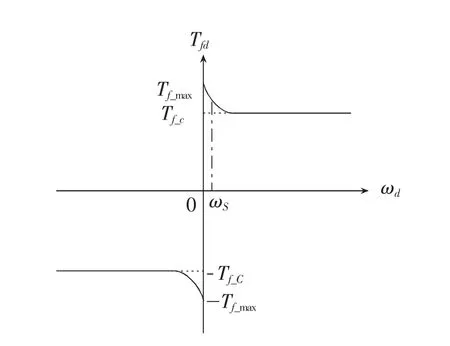
图1 干摩擦力矩

图1中 Tf＿c表示 Coulomb 摩擦转矩，Tf＿max是最大静摩擦力矩，ωS表示摩擦转矩初始大小与Tf＿c的交点，当转速较低时ωS对摩擦特性会产生较大影响，其中Stribeck摩擦模型的数学表达式为：

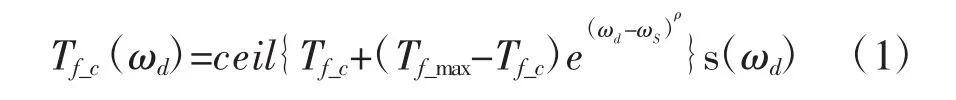
其中，cei（l）表示向上取整函数，ρ表示摩擦系数且范围为（0，1）。

为了方便求解，认为垂直打钻过程钻杆作为弹簧杆，并且忽略钻柱间摩擦与钻杆和井壁间的摩擦，井液流体为无震荡的层流。实际钻井过程中，一般情况将转盘、钻柱、钻铤和钻头组成一个四自由度的模型进行分析，进一步简化整体钻柱系统如图2所示，简化为三自由度的钻柱系统模型。

图2 三自由度钻柱系统

图2中组成部分包括：顶部转动系统、钻杆、BHA（钻头、钻铤组合）。其中，T表示驱动扭矩，它的大小由顶部电机驱动，Tat、Tad分别表示粘性阻尼力矩，Jt、Jm、Jd分别表示顶部转动系统、钻杆、BHA 的转动惯量。K1、K2表示扭转刚度，C1、C2表示旋转阻尼。

通过简化后的模型建立钻杆的数学模型：

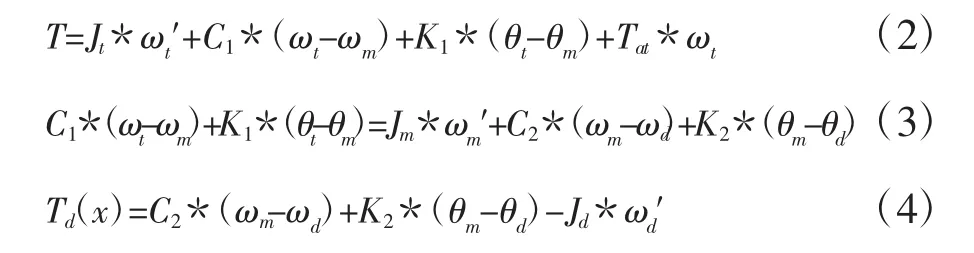
其中，θi，i∈｛t，d，m｝分别是顶部转动系统、钻杆、BHA的角位移，角速度为ωi，T＝U表示通过控制输入（U）调节电机施加动力产生的扭矩。Tat＝Ct＊ωt，Ct是粘性阻尼系数。Td（x）＝Tad（x5）＋Tfd（x）是钻头上的力矩，将系统状态向量表示为 Xi，i∈｛1，2，3，4，5｝定义为：

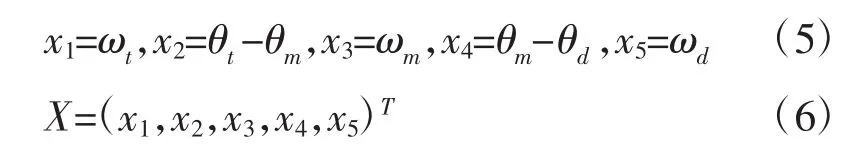
其中，X 表示 Xi的向量系统状态，Tad＝Cd＊x5（Cd为钻具的粘性阻尼系数）接近泥浆对钻头的影响，Tfd是接触岩石摩擦。当速度达到0的临界状态，干摩擦的数学模型为：

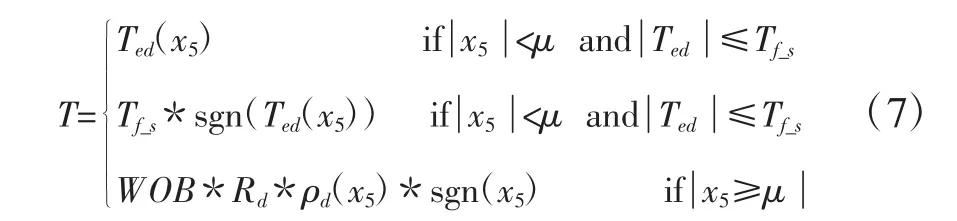
其中，Rd表示钻头的半径，WOB表示钻压，ρ（dx）5是干摩擦系数。当时，钻杆停止状态；当时，钻杆粘滑；当时，钻杆滑移。μ是为了克服0区域盲区设置的角速度参数，Ted为反作用力矩，Tf＿s为此时的静摩擦扭矩，当 Tf＿s＜WOB＊R＊ρ时，钻头才能工作。

Te（dx5）的数学表达式为：

由于钻头的摩擦系数与转动惯量有关，因此通过上述公式描述钻杆的运动方程：

上述公式能够反映出钻柱的扭转行为，而且粘滑现象的发生与参数选择有很大关系。当电机角速度增加、钻压降低可以减少粘滑现象的发生。

2 系统控制设计

自动控制技术指在没有人直接参与的情况下，利用外加的设备或装置，使机器、设备、生产过程的某个工作状态或参数自动地按照预定的规律运行[9－11]。一般自控系统按控制原理不同分为：开环控制和闭环控制。根据实际情况，开环控制局限性比较大，没有自动修正偏差的功能，而且控制精度不高。常用的闭环控制是带有反馈信息的系统控制方式，当被控对象反馈结果出现偏差时，可增加相应的补偿值，使得最终结果趋近于期望值。

2．1 软扭矩控制

在实际钻井过程中，由于钻杆的扭矩是根据钻头转速的大小作为调节的，因此闭环控制的反馈就是钻头速度，当钻头平均扭矩小于顶部扭矩时减小转速，相反则增加转速，这种方法可以避免粘滑振动的发生。在实际钻井中，井下状态总是无法获取，钻井工艺受到一定限制。本文利用能够得到的转盘扭矩、速等信息数据，预测井下部件状态，将预测状态作为闭环控制的补偿信号，从而消除粘滑振动现象，图3显示了软扭矩控制系统的控制回路。

图3 软扭矩控制系统

2．2 实验仿真

本文采用MATLAB 2014b实验软件，用其部件SIMULINK的图形输入方式搭建控制部件，该部件提供了一个GUI图形化的界面，方便用于数学建模。为了验证本文所提出理论方法的可行性，对钻柱系统进一步简化，将其转换为二自由度的模型，钻柱1／3的惯量集中于钻头部分，如图4所示。

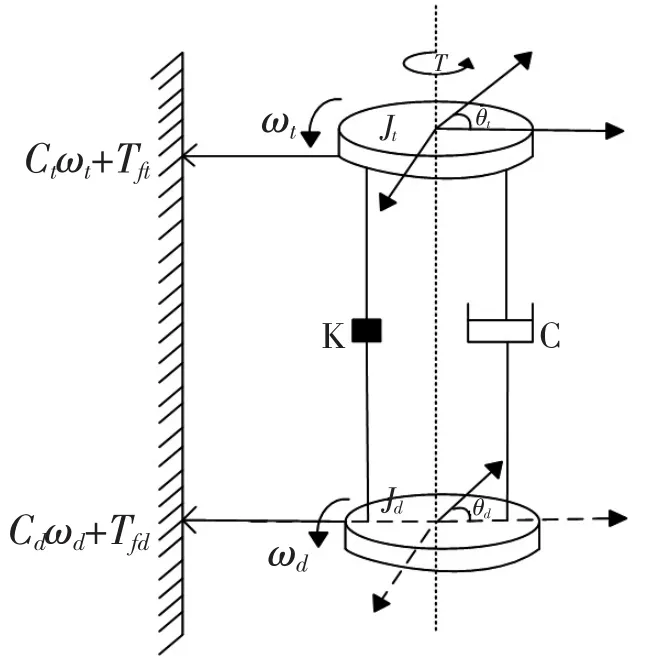
图4 二自由度钻柱模型

利用电机恒速（50r／min）的闭环控制系统，同时将角速度变化为线速度，图5反应了三自由度模型下的仿真结果。从图5可以看出当转盘速度是恒值时，钻头速度与主电机扭矩大幅度上下振动，形成粘滑振动。为了验证本文所提出二自由度模型的优势，对二自由度模型也进行了实验仿真，所得结果如图6所示。

图5 三自由度模型速度与扭矩曲线

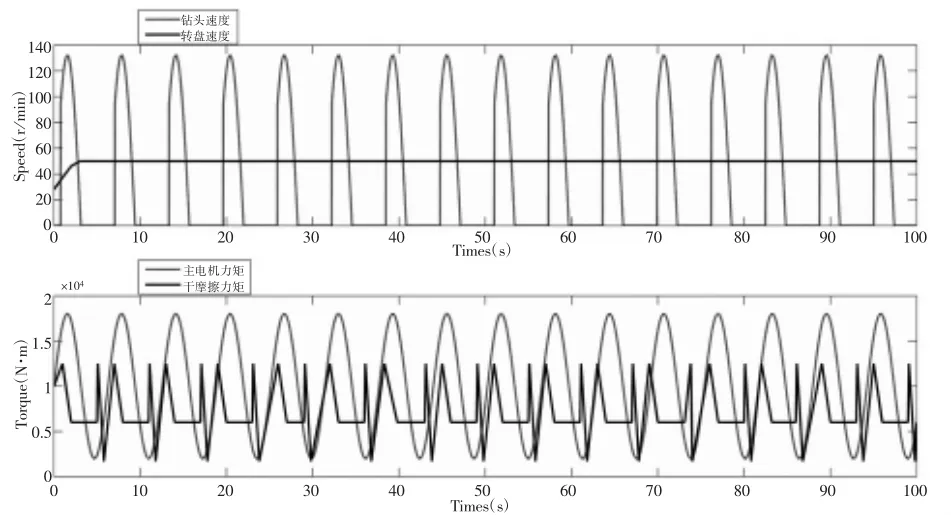
图6 二自由度模型速度与扭矩曲线

比较图5与图6，可以看出简化后的模型只有钻头速度和干摩擦力矩稍微滞后，振荡幅度几乎没变。由于二自由度的转动惯量远远大于三自由度，但弹性系数小于三自由度。从结果看出，二自由度模型可以用于表示钻柱模型，并能简化计算的复杂程度，且不影响最终结果。

在整个模型中，角速度、角位移是无法检测的，计算过程只有速度，为了方便预测角速度、角位移，本文采用非线性公式：

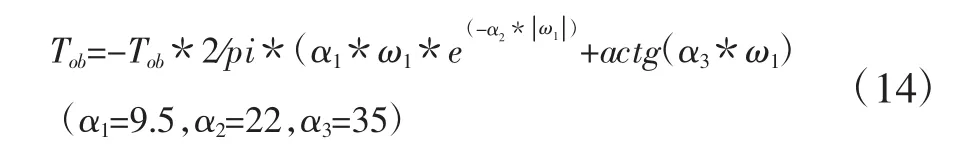
用公式（14）代替非线性摩擦的计算公式（7），为了进一步验证该公式的特性，分别将公式（5）、（14）应用于系统中，得到最终钻柱钻速结果，如图7所示。说明公式（5）与公式（14）具有相似的性质，甚至略微优于原计算，所以这种代替方式是可行的。

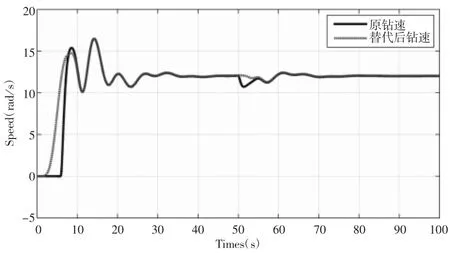
图7 原钻速与代替公式后的钻速对比

本文将公式（14）分别应用于三自由度模型、二自由度模型，在转盘速度一定时，所得钻头转速曲线，如图8所示。

图8 不同自由度下的钻速

根据图8所示，本文提出的方法虽然在转盘速度恒定时也出现钻速波动的情况，但是波动幅度不大且优于三自由度模型。因此，将公式（14）替代原非线性关系可以解决公式（5）需要计算角速度、角位移的情况，进而简化计算。

3 结论

通过理论验证及实验仿真，可以看出二自由度模型能很好地表示钻柱的物理特性。同时本文提出的方法在一定程度上可以改善钻柱系统，使得钻速更加稳定。后续工作将围绕实际应用进行进一步优化，并且尝试在控制方案中应用该理论。