无限滞后测度泛函微分方程的Φ有界变差解的唯一性
2022-01-26丁利波
丁利波
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
1959年,MUSIELAKJ等[1-2]提出了Φ有界变差函数理论,这种理论是一般意义下的有界变差函数理论的发展与推广,而且许多学者对Φ有界变差函数理论进行了深入的研究.文献[3-4]首次将Φ有界变差函数理论与Kurzweil方程理论结合起来,建立了Kurzweil方程的Φ有界变差解的唯一性定理和一类固定时刻脉冲微分系统Φ有界变差解的唯一性.卢金芳等[5]研究了滞后型泛函微分方程的Φ有界变差解的唯一性.Slavik在文献[6]中介绍了一类无限滞后测度泛函微分方程:
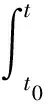
(1)
无限滞后测度泛函微分方程已经被许多学者所研究[7-11].
本文考虑无限滞后测度泛函微分方程初值问题
(2)
Φ有界变差解的唯一性,其中x是取值在Rn上的函数,xs(τ)=x(s+τ),τ∈(-∞,0]表示滞后的长度.
1 预备知识
定义1[12]函数U:[a,b]×[a,b]→Rn称为在[a,b]上是Kurzweil可积的,如果存在I∈Rn,使得对任意ε>0,存在正值函数δ:[a,b]→R+,使得对[a,b]上的任何δ-精细分划D={(τi,[αi-1,αi]),i=1,2,…,k},其中τi∈[αi-1,αi]⊂(τi-δ(τi),τi+δ(τi)), 有
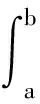
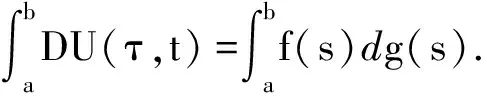
设G是Rn+1中的开集,F:G→Rn是对(x,t)∈G,x∈Rn,t∈R定义的Rn值函数.
定义2[12]函数x:[α,β]→Rn称为广义常微分方程
在区间[α,β]⊂R上的解是指对所有的t∈[α,β],(x(t),t)∈G,且对每个s1,s2∈[α,β],有

成立.
设Φ(u)是对u≥0定义的连续不减函数,且满足Φ(0)=0.对u>0,Φ(u)>0,本文假定Φ(u)满足下列条件:
(c1)存在u0>0及L>0,使得对0 (c2)Φ(u)是凸函数,即 定义3[1]设[a,b]⊂R,-∞ 并称VΦ(x;[a,b])为函数x(t)在[a,b]上的Φ-变差. 定义4设t∈[t0,+∞),称x(t,t0,φ)是无限滞后测度泛函微分方程初值问题(2)的Φ有界变差解是指 2)xt0=φ; 3)x在[t0,+∞)的任何紧子区间上是Φ有界变差函数; 4)当t∈[t0,+∞)时,(xt,t)∈Ω. 定义5设Ω=O×[t0,+∞),函数f:Ω→X属于函数族VΦ(Ω,h,ω),如果f满足以下条件. H1) 存在一个正值函数δ(τ):[t0,+∞)→R,使得对每个区间[u,v]满足τ∈[u,v]⊂(τ-δ(τ),τ+δ(τ))⊂[t0,+∞)及x∈O,有 ‖f(xτ,τ)(g(v)-g(u))‖≤Φ(|h(v)-h(u)|). (3) H2) 对每个区间[u,v],满足τ∈[u,v]⊂(τ-δ(τ),τ+δ(τ))⊂[t0,+∞)及x,y∈O,有 ‖f(xτ,τ)-f(yτ,τ)‖(g(v)-g(u))≤ω(‖xτ-yτ‖)Φ(|h(v)-h(u)|). (4) 其中h:[t0,+∞)→R是不减的左连续函数,ω:[0,+∞)→R是单调递增的连续函数且ω(r)>0,r>0,ω(0)=0. 下面主要介绍无限滞后测度泛函微分方程的Φ有界变差解及其唯一性定理的相关结果: 定义6无限滞后测度泛函微分方程(2)的Φ有界变差解x:(-∞,t0+η]→Rn称为右行局部唯一解,如果对无限滞后测度泛函微分方程(2)的任何满足xt0=yt0=φ的Φ有界变差解y:(-∞,t0+α]→Rn,存在η1>0,使得对t∈(-∞,t0+η]∩(-∞,t0+α]∩(-∞,t0+η1],有x(t)=y(t). 如果无限滞后测度泛函微分方程(2)的每个解x满足xt0=φ是右行局部唯一的,则点(t0,φ)∈Ω称为方程(2)的右行局部唯一点.进一步讲,如果每个(t0,φ)∈Ω是无限滞后测度泛函微分方程(2)的唯一点,则无限滞后测度泛函微分方程(2)具有右行局部唯一性质. 引理1[12]设ψ:[a,b]→[0,+∞)是区间[a,b]上的有界变差函数,h:[t0,+∞)→R是不减的左连续函数,ω:[0,+∞)→R是单调递增的连续函数且ω(r)>0,r>0,ω(0)=0. 如果F(k)+h(b)-h(a)<β,则对任意的ξ∈[a,b],有ψ(ξ)≤F-(F(k)+h(ξ)-h(a))成立,其中F-:(α,β)→R是函数F的反函数. 定理 1设f∈VΦ(Ω,h,ω),其中h是不减的左连续函数,ω:[0,+∞)→R是单调递增的连续函数且ω(r)>0,r>0,ω(0)=0.对每一个u>0,有 (5) 则无限滞后测度泛函微分方程(2)的每个满足xt0=φ,(t0,φ)∈Ω的Φ有界变差解x是右行局部唯一的. 证明设x,y:(-∞,t0+η]→Rn无限滞后测度泛函微分方程(2)的满足初始xt0=yt0=φ的两个Φ有界变差解,其中η>0,则 对任意的ε>0,存在正值函数δ(τ):[t0,t]→[0,+∞),使得对[t0,t]的任何δ-精细分化 D={τi,[αi-1,αi],i=1,2,…,k}, 由定义1及定义5的条件H2,有 由文献[1],有 (6) 令v(t)=VΦ(h,[t0,s]),t0 由ε>0的任意性,有 (7) 其中0<δ (8) ‖x(t)-y(t)‖≤F-(F(A(δ))+v(t)-v(t0+δ)), (9) 显然有 F(A(δ))+v(t0+η)-v(t0+δ)≤F(A(δ))+v(t0+η)-v(t0+). 因此,存在δ0>0,使得对δ∈(0,δ0),不等式F(A(δ))+v(t0+η)-v(t0+)<β成立,由式(9)有 F(‖x(s)-y(s)‖)≤F(A(δ))+v(s)-v(t0+δ). 进一步,有 F(‖x(t)-y(t)‖)-F(A(δ))≤v(t)-v(t0+δ)≤v(t)-v(t0+). 由函数F的定义,对t∈[t0+δ,t0+η],δ∈(0,δ0),有 如果对某个t*∈(t0,t0+η],有‖x(t)-y(t)‖=k>0,对δ∈(0,δ0),使得δ 这与定理中有关函数ω的条件相矛盾,故对任意的t∈(-∞,t0+η),有‖x(t)-y(t)‖=0,因此定理结论成立. 定理 2设f∈VΦ(Ω,h,ω),x:[α1,β1]→Rn,y:[α2,β2]→Rn是无限滞后测度泛函微分方程(2)的两个Φ有界变差解,如果条件(5)成立,且对s∈[α1,β1]∩[α2,β2],有x(s)=y(s),则对所有的t∈[α1,β1]∩[α2,β2]∩[s,b],有x(t)=y(t). 证明因为相交部分[α1,β1]∩[α2,β2]∩[s,b]是形如[s,c],c 本文在之前学者工作的基础上,借助Φ有界变差函数理论和Henstock-Kurzweil 积分的有关结果,讨论了无限滞后测度泛函微分方程的Φ有界变差解的唯一性定理,并对其进行了证明,将有界变差解的相关结论推广到Φ有界变差解.因此,接下来的工作可以继续讨论无限滞后测度泛函微分方程的Φ有界变差解的Lipschitz稳定性和周期性.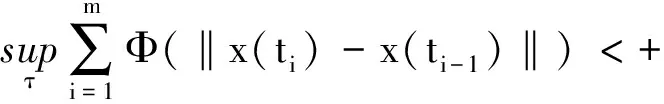
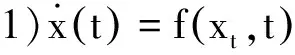
2 无限滞后测度泛函微分方程Φ有 界变差解的唯一性
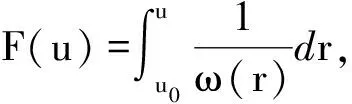
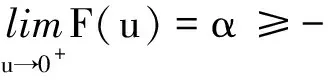


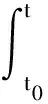
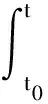
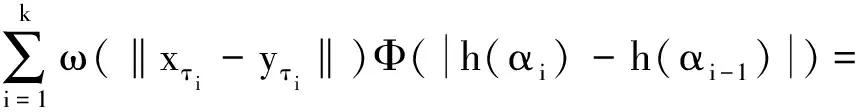
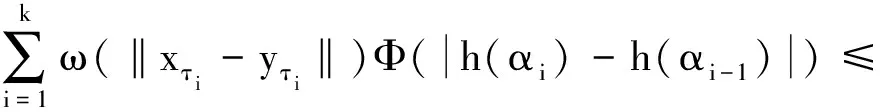
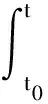
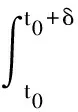
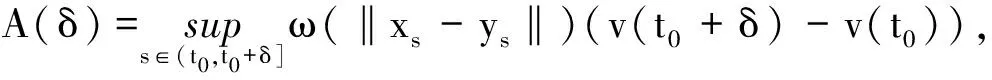
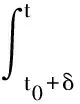
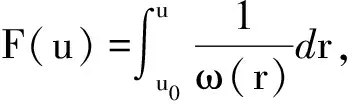
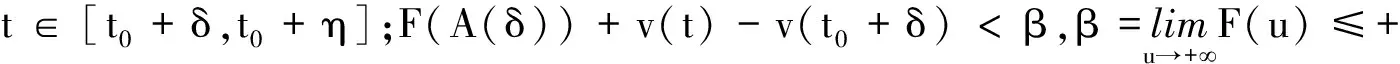
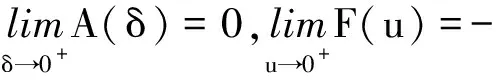
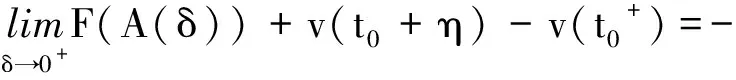
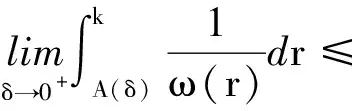
3 结语
