基于类间距离的Logistic序贯多分类的成都空气质量污染分析
2022-01-26李亭亭吕王勇周娇曾诗静
李亭亭,吕王勇,2*,周娇,曾诗静
(1.四川师范大学数学科学学院,成都 610068;2.可视化计算与虚拟现实四川省重点实验室,成都 610068)
随着社会经济的不断发展,人类活动的逐渐增加,于是产生了各种各样的污染,对环境造成了巨大的危害,因此环境问题也愈发严重。其中空气污染是比较严重环境问题之一,空气质量的好坏与人们的生活息息相关,所以治理空气污染是保护环境的重要决策之一。
治理空气污染,首先需要了解空气中的污染物种类,这些空气污染物产生的原因以及主要空气污染物对空气质量产生的影响等,这些问题一直都是中外学者研究的热点,并且成果显著。张宝林等[1]利用遥感影像与地面观测数据研究了沙尘天气对内蒙古草原城市锡林郭勒盟大气环境和空气污染物浓度的影响,并为沙尘天气环境影响评价提供理论依据;刘玲等[2]利用长三角城市群地面气象观测数据,对长三角城市群某一次重污染天气过程的气象成因以及污染物路径分析,并得出大气化学模式WRF-Chem可较好地模拟出PM2.5浓度的变化过程,可用作长三角城市群重污染天气预报的业务模式;徐梦辰等[3]通过运用统计分析、趋势检验及相关分析等方法研究了济南市执行新环境空气质量标准后各时段城市空气质量及6项污染物浓度变化趋势,并在此基础上识别了济南市是PM10、PM2.5和O3污染为代表的复合型大气污染特征。
并且研究这些问题的方法多种多样,学者们利用不同的方法对问题进行探讨。李娜等[4]为了研究长春市采暖期与非采暖期PM2.5中多环芳烃(polycyclic aromatic hydrocarbons,PAHs)的浓度和来源结合比值法进行 PAHs 来源解析,并通过美国国家环境保护局健康风险评价模型进行健康风险评估,为长春市大气污染综合防治和环境管理提供科学依据;谢劭峰等[5]利用多元线性模型对南宁市空气污染物PM2.5的浓度值进行预测,并且结果表明该预测模型能够适用于南宁市空气污染物PM2.5的监测和预报;张晓凯等[6]利用统计回归分析的方法对大气颗粒物的粒径与数量进行分析,绘制相应粒径变化柱状图,再根据大气颗粒的检验结果推断大气颗粒物化学组成和来源,提出控制大气颗粒物PM2.5、PM10污染的有效策略。
空气质量是关乎人民生活质量、身体健康的重要因素之一,因此现提出基于类间距离的序贯Logistic多分类算法(sequential Logistic multi-classification algorithm based on distance between classes,SMLG)来分析影响空气质量的主要污染物。该方法首先通过类间距离对数据进行聚类,将多分类问题转化为多个二分类的问题,再使用二分类Logistic进行分类。利用该方法对成都市2019年4月—2020年5月的空气质量数据分类后,再对影响成都空气质量数据进行逐步回归,最后根据SMLG的分类正确率得出对空气质量影响最大污染物。
1 基于类间距离的序贯Logistic多分类算法
存在一个数据集B,样本量为m,该数据由B1,B2,…,Bk这k类数据构成,每类数据的样本量为ni,i=1,2,…,k。若采用Logistic多分类回归对数据集B进行分类,则因变量Y取值为1,2,…,k,自变量为X=(X1,X2,…,Xn)是n维变量。根据Y的取值为有序或无序,可以将Logistic多分类分为两类,一类是有序Logistic多分类[7](ordinal Logistic multiple classification,OMLG),另一类是无序Logistic多分类[8](unordered multi-class Logistic,UOMLG)。
1.1 有序Logistic多分类
当因变量Y为有序变量时,Logistic多分类应该采用有序Logistic多分类。该分类原理是将看成第一类,剩下的类看成第二类,再利用二分类Logistic回归进行分类。设给定X的条件下,Y取j的概率为Pj=P(Y=j|X),且P1+P2+…+Pk=1。j=1,2,…,k,现将k类分成{1,2,…,j}和{j+1,j+2,…,k}两类,其中j=1,2,…,k-1。再利用两分类Logistic回归模型进行分类,则将有序多分类Logistic回归模型转化为多个二分类的Logistic回归模型,共拟合k-1个二分类Logistic回归方程,公式为

(1)
式(1)中:β0j和βij分别为第j个二分类Logistic模型的截距和偏回归系数。根据极大似然估计可以求出β0j和βij的估计值
将其代入式(1)中经过运算就可得到P(Y=j|X),j=1,2,…,k的值。然后,依据概率最大原则,比较各P(Y=j|X),j=1,2,…,k的值。
1.2 无序Logistic多分类
当因变量Y为无序变量时,应采用无序Logistic多分类。该方法的原理是将某一类设为主类别,然后同其他类分别进行二元Logistic回归,建立k-1个二元Logistic回归模型。设给定X的条件下Y取j的概率为Pj=P(Y=j|X),j=1,2,…,k,且P1+P2+…+Pk=1。把B中第k类看成主类别,然后将其他k-1个类和所选择的主类别分别进行二元Logistic回归回归,共拟合k-1个独立二元Logistic回归模型,公式为
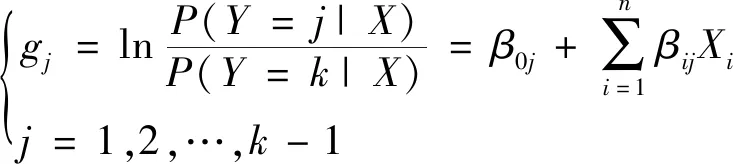
(2)
最后通过推导求出P(Y=j|X),j=1,2,…,k的概率,依据概率最大原则,比较各P(Y=j|X),j=1,2,…,k的值。
1.3 SMLG方法
由于有序多分类和无序多分类在进行分类时都存在分类精度稍差和大数据的运行效率较低的问题。基于此提出SMLG方法,它是利用聚类分析中的快速聚类的方思想,根据类间距离(类与类的距离)来进行聚类。所以首先需要求解类间距离。
1.3.1 类间距离
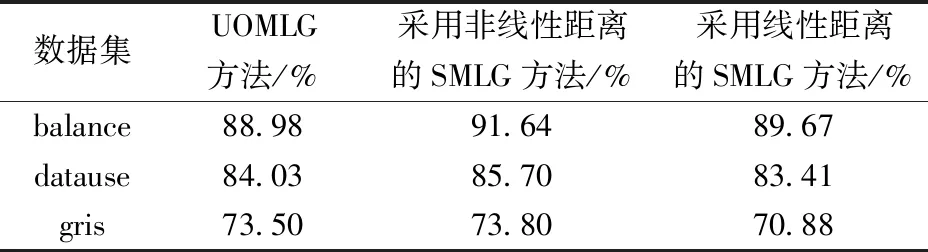
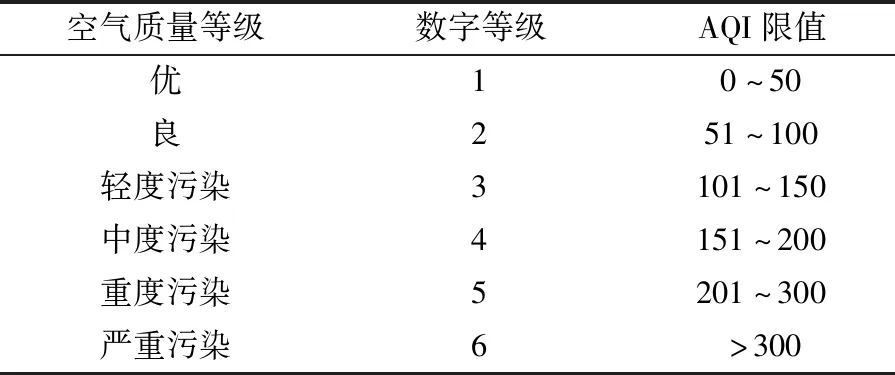
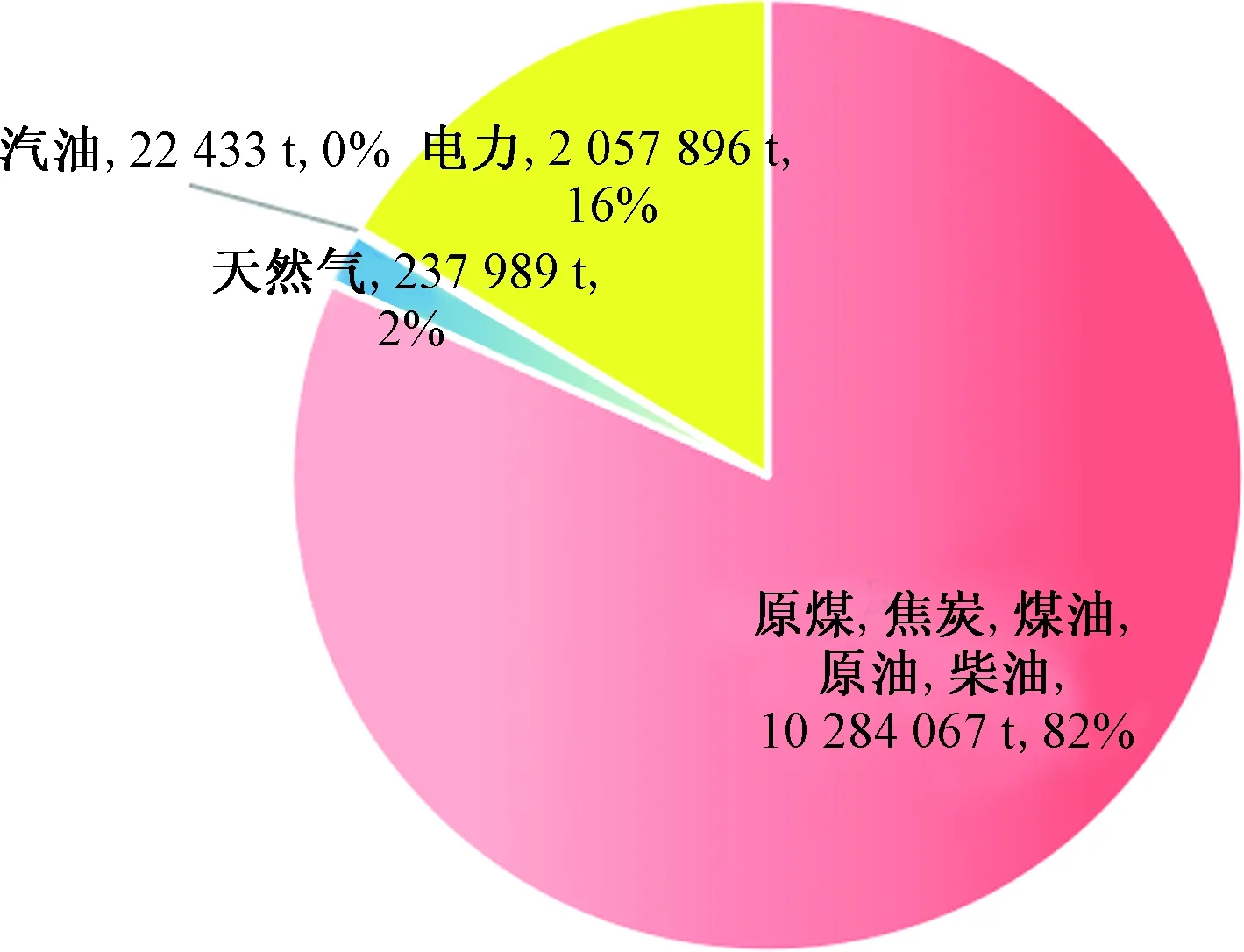
数据集B由B1,B2,…,Bk这k类数据构成,每类数据的样本量为ni,i=1,2,…,k,可运用式(3)计算出数据集B中任意两类Bp与Bq之间的距Dpq(p,q∈1,2,…,k且p (3) 表1 常见的核函数Table 1 Common kernel functions 1.3.2 SMLG方法 SMLG方法的提出是为了解决传统Logistic多分类出现的精度差、效率低、使用受限的问题。该方法首先是计算类与类之间的距离,选出最小距离。假设数据集B中Bi和Bj(i,j∈1,2,…,k)的距离最小,则可将Bi和Bj聚为一个新的类别“Bij”。把“Bij”看成是第一类,然后将其他k-2个类别看成第二类,再进行二元Logistic回归。这时Y1={0,1},X1=(X11,X21,…,Xn1)是n维变量。下面对该二元Logistic回归模型进行推导。 在给定X的条件下,Y1=0和Y1=1的概率和为1,即 P(Y1=0|X1)=1-P(Y1=1|X1) (4) 再引入Logistic函数后可得 =e-f1 (5) (6) P(Y1|X1,β)=[hβ(X1)]Y1[1-hβ(X1)]1-Y1 (7) 根据式(7)可以得到似然函数为 (8) 对式(8)取对数可得 (9) 对式(9)求导得 (10) 第二个Logistic回归函数为 =e-f2 (11) 对式(11)同时取对数可得 (12) 通过上述方法就分开了Bi和Bj,在剩下的k-2类中重复使用上述方法,这样就可以通过k-1个二元Logistic回归完成分类,其回归模型为 (13) 最终根据回归的结果统计该方法的正确率即可该方法分类模型如图1所示。 图1 分类模型图Fig.1 Classification model diagram 对SMLG方法进行数据仿真实验,验证其方法的有效性。所采用的实验数据是UCI(university of California in Irvine)[9]机器学习数据库中的balance-scale数据集(以下简称balance数据集)、datauser数据集、Grisoni_et_al_2016_EnvInt88数据集(以下简称gris数据集)、seane数据集、crowdsourced mapping数据集、avila数据集和数据网[10]中的Beijing数据集(里面是北京景区空气质量的数据),并用R软件进行实验。 表2所示的数据集都是类别为3的数据,其中balance数据集、datause数据集和gris数据集都是非线性数据集。通过对比发现,当数据为非线性时,如果采用线性距离的SMLG方法,其正确率会比采用非线性距离的SMLG方法正确率低。因此该方法的优势就不能展现,所以在使用SMLG方法时距离的选择十分重要。 表2所示的不同数据集采用SMLG方法和UOMLG方法的运行时间及正确率。通过对比会发现对于小数据而言,UOMLG方法运行时间比SMLG方法运行时间要小,是因为SMLG运行时会对数据进行分类和聚类的操作,导致运行时间增加。但对于大数据,可以从表2中发现SMLG方法运行时间比无序多分类更加节省,这是因为数据集较大时SMLG方法会对数据进行分类再聚类,这样大数据就变为多个小数据,而小数据的运行时间少,就算再加分类再聚类运行时间总时间也比UOMLG方法运行时间少。 表2 3种数据线性距离和非线性距离SMLG方法分类正确率的对比Table 2 Comparison of the classification accuracy of three data linear distance and nonlinear distance SMLG methods 注意表3中的Beijing数据集是采用的有序Logistic多分类方法,因此Beijing数据集中的UOMLG正确率其实是OMLG正确率。通过展示的SMLG方法和UOMLG方法的分类正确率,说明利用SMLG方法进行多分类时,提高了分类的正确率。 表3 多种数据的SMLG方法和UOMLG方法运行时间及正确率比较Table 3 Comparison of running time and accuracy of SMLG method and UOMLG method for multiple data 从天气后网站[11]搜集了从2019年5月1日—2020年4月30日成都空气质量数据,共334 d的空气质量。该数据包括空气质量等级(air quality index,AQI)值及PM2.5、PM10、O3、SO2、NO2和CO的浓度。AQI是根据《环境空气质量指数(AQI)技术规定(试行)》(HJ 633—2012)中大气污染物浓度限值划分为优、良、轻度污染、中度污染、重度污染和严重污染6个等级,用数字1、2、3、4、5、6表示,具体见表4。由于该数据集中只有优、良、轻度污染和中度污染这4种空气质量数据,所以该数据集的AQI值为1、2、3和4。 表4 AQI值及对应的等级Table 4 AQI size value and corresponding level 步骤一对成都空气质量数据集进行相关性分析,利用R软件画出散点图,如图2所示。变量与变量之间的散点图可以体现这两个变量之间的线性关系。例如,图2中第2排第3副小图展示的就是PM2.5和PM10的散点图,可以观察散点的分布类似一条直线,因此PM2.5和PM10有着较强的线性关系。因此可知PM2.5和PM10之间呈明显的线性相关,而PM2.5和CO、PM10和CO、PM10和NO2之间呈不明显的线性相关,因此其数据总体呈非线性的关系。 图2 成都气象数据的相关性散点矩阵图Fig.2 Correlation scattered matrix diagram of Chengdu meteorological data 图3 SMLG分类思想图Fig.3 The map of SMLG classification idea 步骤三将测试集代入已训练出的分类器中,重复上述步骤100次,最后得出100次的正确率的平均值,以此来作为SMLG的正确率。现对比成都空气质量数据采用OMLG方法和SMLG方法的正确率,如表5所示。 表5 成都市空气质量数据SMLG和UOMLG的分类正确率Table 5 Classification accuracy of air quality data in Chengdu based on SMLG and UOMLG 对成都市2019年5月1日—2020年4月30日的空气质量数据采用SMLG方法进行分类后,并记录其正确率。通过逐步分类的方法,对影响空气质量的污染物因子进行分析,得出对空气质量影响较大的污染物种类。该数据由AQI值及PM2.5、PM10、O3、SO2、NO2和CO的浓度构成,通过逐步分类后,得出影响成都空气质量最重要的污染物是PM2.5、PM10、NO2、O3,其分类正确率为93.34%。由于逐步分类采用SMLG方法共进行了63次分类,现只展示部分逐步分类结果,见表6。 表6 影响AQI的污染物分析Table 6 Analysis of pollutants affecting AQI 由表6可知,对污染物PM2.5、PM10、NO2和O3重新采用SMLG方法进行分类后,其分类正确率与其他污染物因子通过SMLG的分类正确率相比,正确率最高,由此可以得出对成都空气质量综合影响较大的污染物是PM2.5、PM10、NO2和O3。 2.3.1 重要污染物形成原因分析 成都市作为西部城市中重要的经济交通枢纽、文化艺术中心,人口密集,工业繁荣,但机动车量大,工业生产等造成的人类活动对空气质量产生重要影响。近年来随着成都市的城市发展逐渐完善,工业逐渐成熟,然而工业化的发展对能源的需求是巨大的,进而能源的消耗造成的环境污染是不可避免的。随着政府不断推进“绿色发展”“绿水青山”“可持续发展”等理念,从2015年起,虽然煤炭、原油、柴油等能源的使用在逐年减少,但其在总体能源消耗中占比中仍然最大。正是由于工业化建设中这些能源的使用,成为空气中二氧化硫和烟(粉)尘排放量的重要来源。比如,2018年使用煤炭原油类的能源占总体使用能源的82%[12],如图4所示。同时随着成都市的机动车保有量的增加,截至2019年成都市汽车保有量超过500万辆,成为全国位居第二的城市[13]。而汽车尾气中的硫化物等的排放对成都空气质量的影响较大,虽然空气中的二氧化硫和烟(粉)尘排放量在2015—2019年都在逐渐减少,但其总体占比仍为废气含量中的第一。 图4 2018年成都市能源消费占比Fig.4 Proportion of Chengdu’s energy consumption in 2018 同时气候也会对空气质量造成一定的影响,成都平原四季分明,日照少,主要受暖湿亚热带太平洋东南季风影响,气候潮湿温润。潮湿的气候会导致PM2.5吸湿使得PM2.5的二次转化变快,导致其浓度升高,加重空气污染程度[14]。 成都市位于四川盆地西部,四周环绕着高原山地,龙泉山在其东南侧,龙门山在其西北侧,其独特的地理环境造成了成都市特殊的臭氧污染,表现为高浓度O3与PM2.5的复合污染特征[15]。同时因为四川盆地位于青藏高原附近,受空气流动,气温变化及气压变化的影响导致夏季经常出现晴朗少云、高温低湿的环境,而这样的环境有利于臭氧发生光化学反应,此外成都市表现为中低层大气[16],下沉气流建立了静稳天气形势,导致臭氧污染物在近地层积聚进而形成持续污染。 根据空气质量指数AQI对成都市2019年5月—2020年4月的空气质量数据进行分类,分类方法采用基于序贯的多分类Logistic回归(SMLG),并对该模型进行可行性分析。再利用SMLG对成都市空气质量数据进行分类并统计分类正确率,最后利用逐步回归对影响AQI的污染物因子做分析。 结果表明,污染PM2.5、PM10、NO2和O3对AQI的综合影响力最强,因此影响成都空气质量的重要污染物是PM2.5、PM10、NO2和O3这4种。其实影响成都市空气质量的因素错综复杂,虽然特殊的地理位置和气候条件在一定程度上会导致空气质量发生改变,但对空气质量影响更大的是人类活动,只有积极应对和严格监管,成都市的环境空气质量才会得到改善。 成都气象监控部门应该加强对工业生产中废气排放的监督,同时政府也要加强清洁能源使用的推广,加强对汽车使用的治理,对粉尘的防范,给人们创建一个健康的生活环境。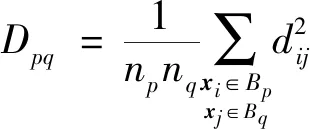
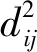



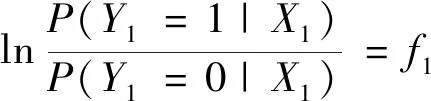

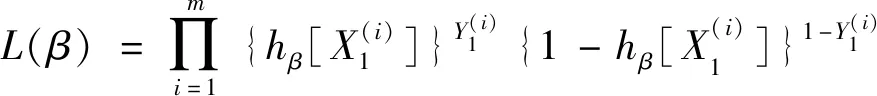
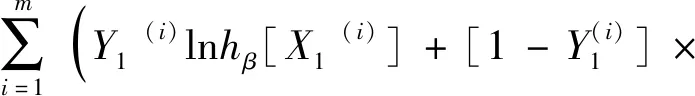
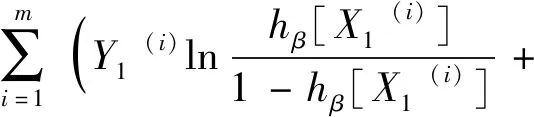
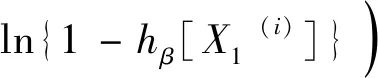
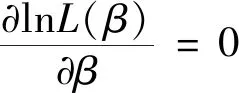
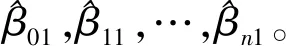
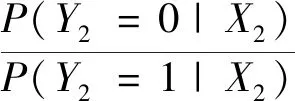
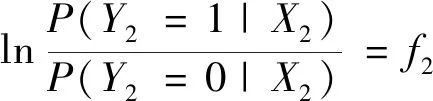


2 实证分析
2.1 方法验证

2.3 实证分析

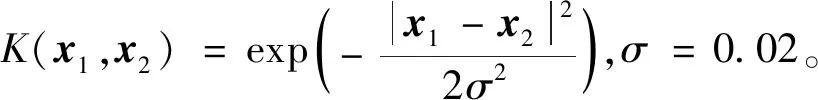


2.3 影响AQI的污染物分析

3 结论与建议
