深圳PM2.5浓度变化趋势及其月尺度预测方法

何钰清，李磊,2,3*，杨红龙，兰紫娟，邵应泉，张文海

(1.中山大学大气科学学院，珠海 519082；2.环珠江口气候环境与空气质量变化广东省野外科学观测研究站，珠海 519082；3.热带大气海洋系统科学教育部重点实验室，珠海 519082；4.深圳市国家气候观象台，深圳 518040；5.深圳市环境科学研究院，深圳 518001；6.珠海市国家气候观象台，珠海 519000；7.深圳强风暴研究院，深圳 518057)

改革开放以来，中国经济飞速发展，伴随而来的大气环境问题引人关注[1-5]。特别在经济与工业发达的地区，以PM2.5浓度增加为主要表征的大气污染问题一度相当严重[6-9]。当前尽管O3污染问题越来越突出，但PM2.5污染依然不可忽视，仍有大量研究从PM2.5污染变化特征、影响因素及形成机制等多方面对此进行持续探讨[10-11]。

深圳是珠三角城市群的一座特大城市，经济繁荣，人口密度大，城市化率高，在过去几十年里，珠三角地区大气环境质量曾严重恶化[12-13]，深圳市的灰霾天数也曾在2004年一度达到187 d。近年来，珠三角地区采取了更加严格的污染防治措施，并且取得了显著成效，空气质量逐年上升，PM2.5浓度显著下降，年平均浓度已达到国家二级标准[14-15]。与此同时，深圳的空气质量也呈逐年提升的趋势[16-17]，当前已成为中国四大一线城市中大气环境质量最好的城市[18]。但即使是在PM2.5污染已经大大改善的今天，深圳仍然会在不利气象条件下出现PM2.5和O3浓度同时上升的复合型污染[19]，且局地小尺度的PM2.5污染过程仍不时发生[20]。

空气质量固然与排放源有密切联系，但气象因素也是污染物形成、传输及沉降等环节的重要原因[21-25]，从气象因素的角度分析大气污染的规律和机制，有助于为大气污染防治提供科学支撑。然而，过去关于深圳的研究多针对典型污染过程[13,26-27]，而基于长期资料从气候角度分析PM2.5浓度与气象因子关系的研究并不多见。尽管也有研究者针对某个季节或某个特定年份分析PM2.5浓度与气象因子的关系，并获得了极有启发性的成果[28]，但这些研究所用资料时段偏短，仍有进一步提升的空间。

利用较长时间段的数据，从气候角度探讨气象要素与污染的关系有重要意义。特别是以“月”为时间单元统计分析气候与PM2.5浓度的关系，有助于月尺度环境气象条件的预报和评估，地方政府可据此提前计划，采取相应的污染排放管控措施，为当地大气环境质量提升工作提供科学指导。基于此，利用2012—2019年深圳市PM2.5浓度监测数据以及相应时间段的气候监测数据，分析了深圳市PM2.5浓度的变化特征及其与气象要素的关系，并进一步建立基于多元线性回归的预测模型，以期对月尺度大气污染防控提供参考。

1 材料与方法

PM2.5数据为深圳市环境监测站11个观测点记录的2012—2019年日均PM2.5浓度数据(图1)，经过计算数值平均得到代表深圳市的日均PM2.5浓度数值。灰霾日数、降水量、降水日数、平均相对湿度、最小相对湿度、平均风速、主导风向、偏北风频率、最高温度及最低温度等逐月气象数据则来自深圳市国家气候观象台在2012—2019年期间发布的逐月气象监测公报，气象数据观测地点为深圳市国家基本气象站，该站资料代表深圳参与世界气象组织(World Meteorological Organization，WMO)的全球资料交换。中国《环境空气质量标准》(GB 3095—2012)规定一级PM2.5浓度限值为15 μg/m3(年平均)和35 μg/m3(日平均)，二级PM2.5浓度限值为35 μg/m3(年平均)和75 μg/m3(日平均)。世界卫生组织(World Health Organization，WHO)对PM2.5浓度设置的标准为：年平均浓度10 μg/m3，日平均浓度25 μg/m3。

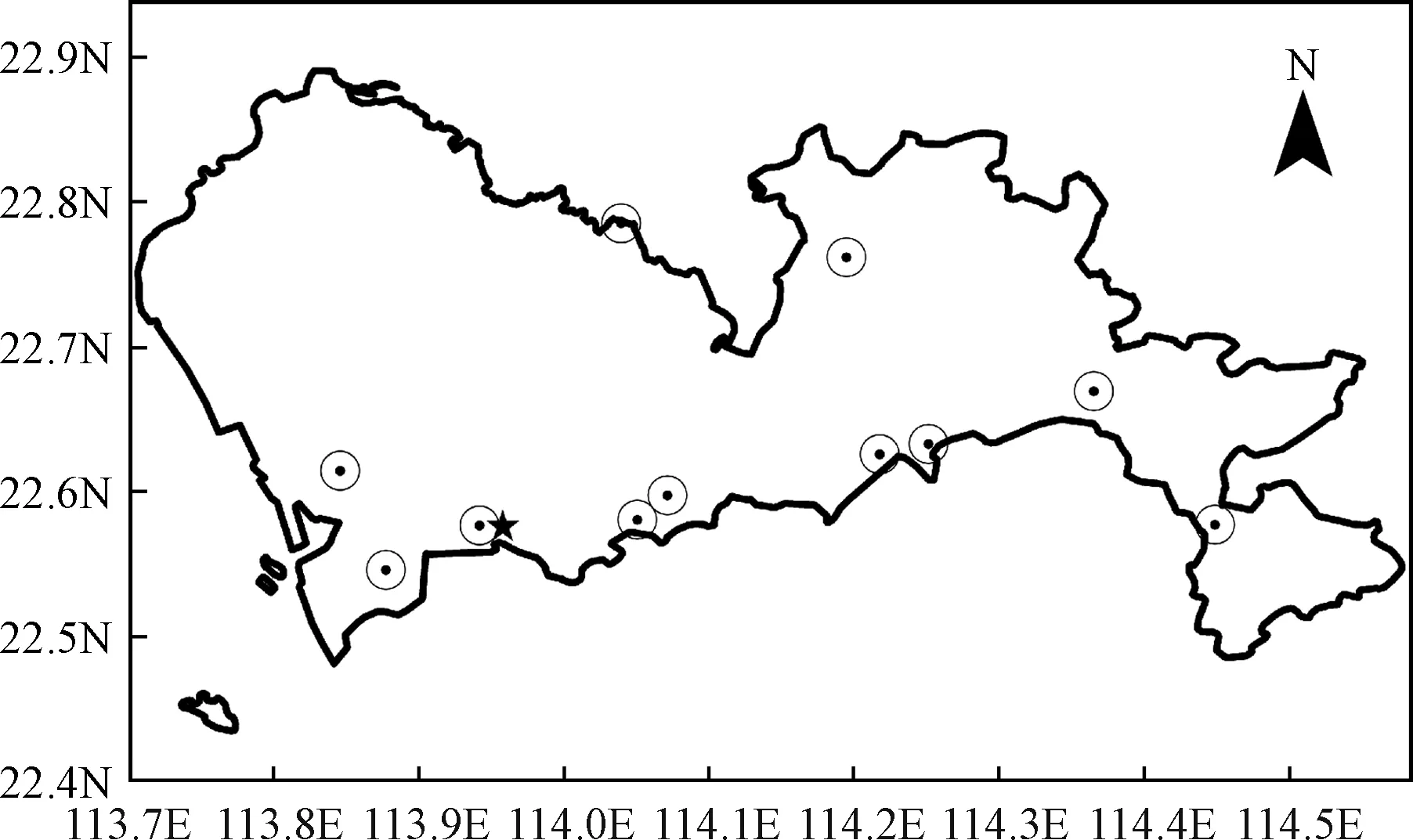
圆圈代表环境监测站点；五角星代表气象站图1 数据来源站点Fig.1 Sources of data

多元线性回归分析是应用较为广泛的统计方法，可用于研究因变量与多个自变量的关系，建立多元线性回归模型可较好地解释以及估计因变量的值，其一般形式为

Y=β0+β1x1+β2x2+…+βmxm+ε

(1)

式(1)中：Y为因变量；x1、x2、…、xm为自变量；β1、β2、…、βm为回归系数；β0为回归常数；ε为随机误差。尝试基于多元线性回归分析建立PM2.5月均浓度的预测方程，以期为相关的环境预测和环境管理提供参考。

2 结果与分析

2.1 PM2.5浓度变化特征

从年平均数据来看[图2(a)]，2012—2019年深圳PM2.5污染改善明显，雾霾天数也大幅下降。8年来PM2.5浓度从37.01 μg/m3下降至24.16 μg/m3，平均每年下降约1.62 μg/m3，而雾霾天数也从77 d降至9 d。从月尺度观察[图2(b)]得到，月均PM2.5浓度有明显的季节性变化特征，在每年干季(每年1—3月和10—12月)的值明显高于同年在雨季(每年4—9月)的。从年平均图可观察到PM2.5浓度在2013年和2017年都有所反弹，年平均值比上一年分别增加了2.58 μg/m3以及1.07 μg/m3，主要是2013年1月、12月以及2017年12月PM2.5浓度增加所致。而雾霾天数只在2013年有所增加，在2017年没有与PM2.5浓度同步上升。之所以出现这种情况，有两个可能的原因：一是较高浓度的PM2.5污染可能集中在了少数某些时间段，特别是统计表明2017年日均PM2.5浓度大于35 μg/m3的天数比2016年多9 d；二是深圳市气象部门在2017年完成了云能天的观测自动化改革，而能见度观测方式的改变，给极度依赖能见度数据的灰霾天数统计带来了不确定性。

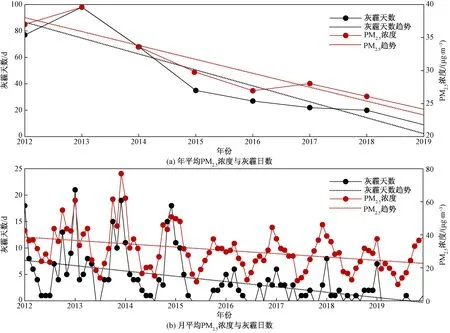
图2 2012—2019年平均以及月平均PM2.5浓度与灰霾日数Fig.2 Average and monthly average PM2.5 concentration and haze days from 2012 to 2019

2.2 PM2.5浓度在干季和雨季的变化特征

结合《环境空气质量标准》(GB 3095—2012)以及WHO标准，分别统计了干季和雨季的PM2.5浓度日均值在不同区间的频率(图3)。2012—2019年，日均PM2.5浓度超过国家二级标准限值(75 μg/m3)的概率呈波动下降趋势，最终在2019年降为零；雨季日均PM2.5浓度达到国家一级标准(<25 μg/m3)的频率逐年递增，到2019年增至88%，干季的这一频率也大致呈递增趋势，但在2013年以及2017年有所上升，且同年的高浓度污染(PM2.5浓度>75 μg/m3)天数也有所增加，表明PM2.5浓度的反弹主要发生在干季。综上所述，深圳细颗粒物污染主要出现在干季，而干季PM2.5浓度的整体下降比雨季明显，可见深圳市大气环境治理的成果较为显著。

图3 2012—2019年干季与雨季24 h内PM2.5浓度分布Fig.3 24 h PM2.5 concentration distribution in dry and wet seasons from 2012 to 2019

2.3 PM2.5浓度与气候要素的关系

2.3.1 PM2.5浓度与风场的关系

图4给出了PM2.5月平均浓度与月平均风速及偏北风占比的变化曲线。与以往研究发现不同，2012—2019年深圳市月平均风速与PM2.5浓度相关系数为0.12，表明在此期间，深圳的月平均风速与PM2.5浓度呈微弱的正相关关系。观察图4中风速与PM2.5浓度曲线变化趋势，发现二者确实整体上都呈振荡下降趋势，从而导致计算得到的相关系数为正。而2012—2019年，深圳市的月平均风速呈略微减弱趋势，可能与深圳市的城市化进程导致测站周围粗糙度增加有关[16]，因此二者之间的相关系数无实质性意义，且不能通过显著性检验。受南亚热带夏季风的影响，深圳在雨季的主导风向为来自海上的西南风，有利于PM2.5浓度的下降，而干季的主导风向则是东北季风。与孙天乐等[29]的研究结果一致，发现外来源的输送是影响深圳大气环境质量的主要原因，利用后向气流轨迹模型HYSPLIT对2017年影响深圳的PM2.5源区进行了回算分析(图5)，表明深圳东北方向的惠州地区的污染物最易输送至深圳。进一步统计深圳市每月的偏北风频率发现其与PM2.5浓度呈较好的正相关，相关系数为0.54，且通过α=0.01的显著性检验。从月尺度上看，相比于风速，偏北风频率更能体现风场对PM2.5浓度的影响。

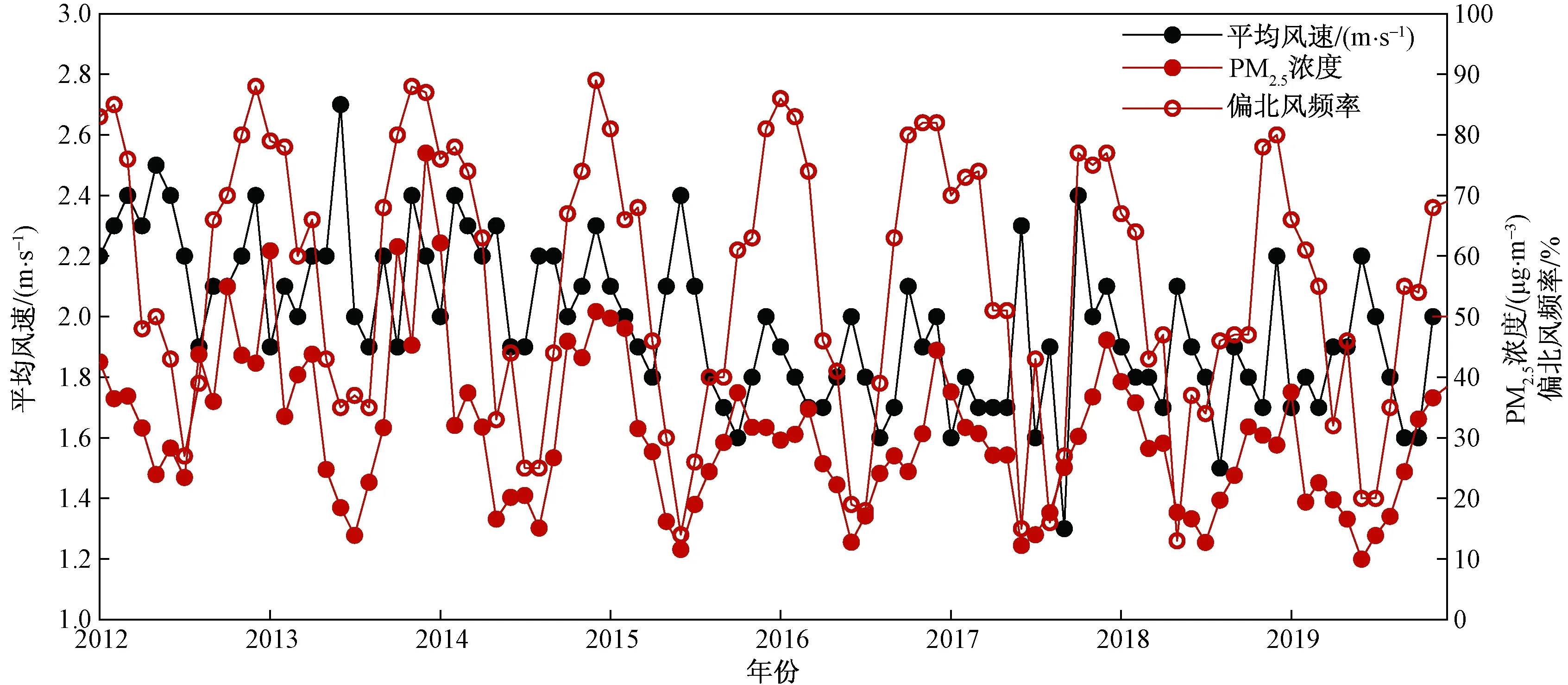
图4 2012—2019年月平均风速与偏北风频率以及月平均PM2.5浓度Fig.4 Monthly mean wind speed,northerly frequency and monthly mean PM2.5 concentration from 2012 to 2019

2.3.2 PM2.5浓度与平均气温的关系

深圳市属于典型的亚热带季风气候，雨季高温高湿，强对流天气易发，对污染物的清除有较好的推动作用，而干季温度较低，冷空气活动频繁，研究表明冬季的PM2.5污染过程往往跟冷空气活动有关[20,30]。统计发现2012—2019年雨季平均温度为27.3 ℃，干季的平均温度为19.6 ℃，深圳的月平均温度为13.7～29.6 ℃(图6)，受季节变化的影响，月平均温度与PM2.5浓度呈较好的负相关，相关系数为-0.64并且通过了α=0.01的显著性检验。月平均气温的高低可在一定程度上对月尺度PM2.5浓度进行预测。

2.3.3 PM2.5浓度与降水以及相对湿度的关系

降雨是影响大气环境质量的重要因素之一，可以使得大气中悬浮的颗粒物以湿沉降的方式从空气中清除。深圳市降雨主要集中在汛期(4—9月)，月降雨日数与月降雨量均与PM2.5浓度呈负相关性(图7)，相关系数为-0.68以及-0.60，均通过α=0.01的显著性检验。空气相对湿度也是影响PM2.5浓度的重要因素之一，以往有研究发现深圳1—3月(非降雨日)相对湿度较高时更容易出现霾天气[31]，有大量针对具体污染过程的研究表明，相对湿度较高有利于细颗粒物的吸湿增长，从而导致PM2.5浓度的升高。与前人研究结果相反[22]，统计深圳的月平均相对湿度(图8)，发现其与PM2.5浓度呈现出显著的负相关，相关系数为-0.73，并且通过了显著性为0.01的检验。出现这一结果的原因是研究的对象是月尺度气候要素，而相对湿度的高低可在一定程度上反映来自海上洁净气流的多少，它与具体到某个时刻的局地湿度条件是否有利于细颗粒物吸湿增长有本质区别。以上分析表明，月降雨日数、月降雨量以及月平均相对湿度都可作为预测PM2.5浓度月均值的良好因子。

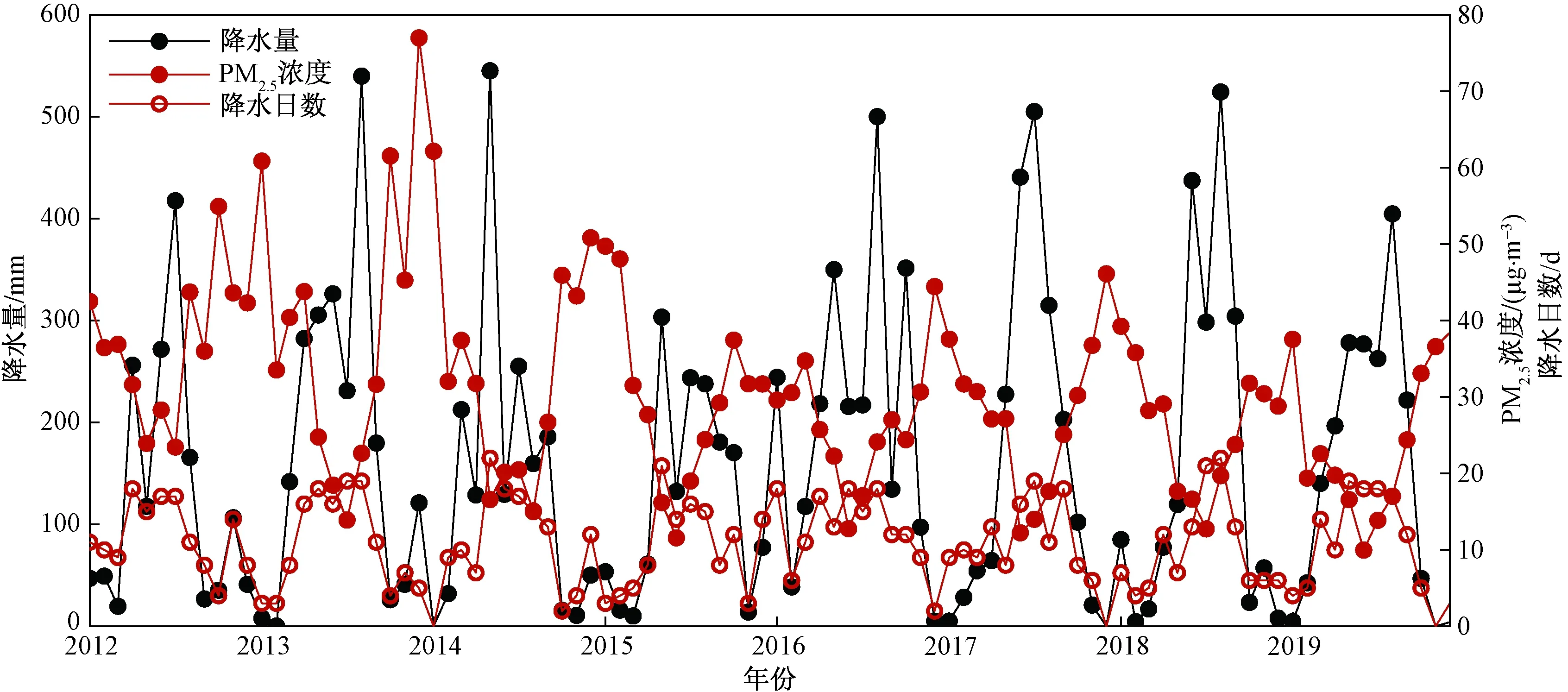
图7 2012—2019年月降雨日数与月降雨量以及月平均PM2.5浓度Fig.7 Monthly rainfall days,monthly rainfall and monthly average PM2.5 concentration from 2012 to 2019

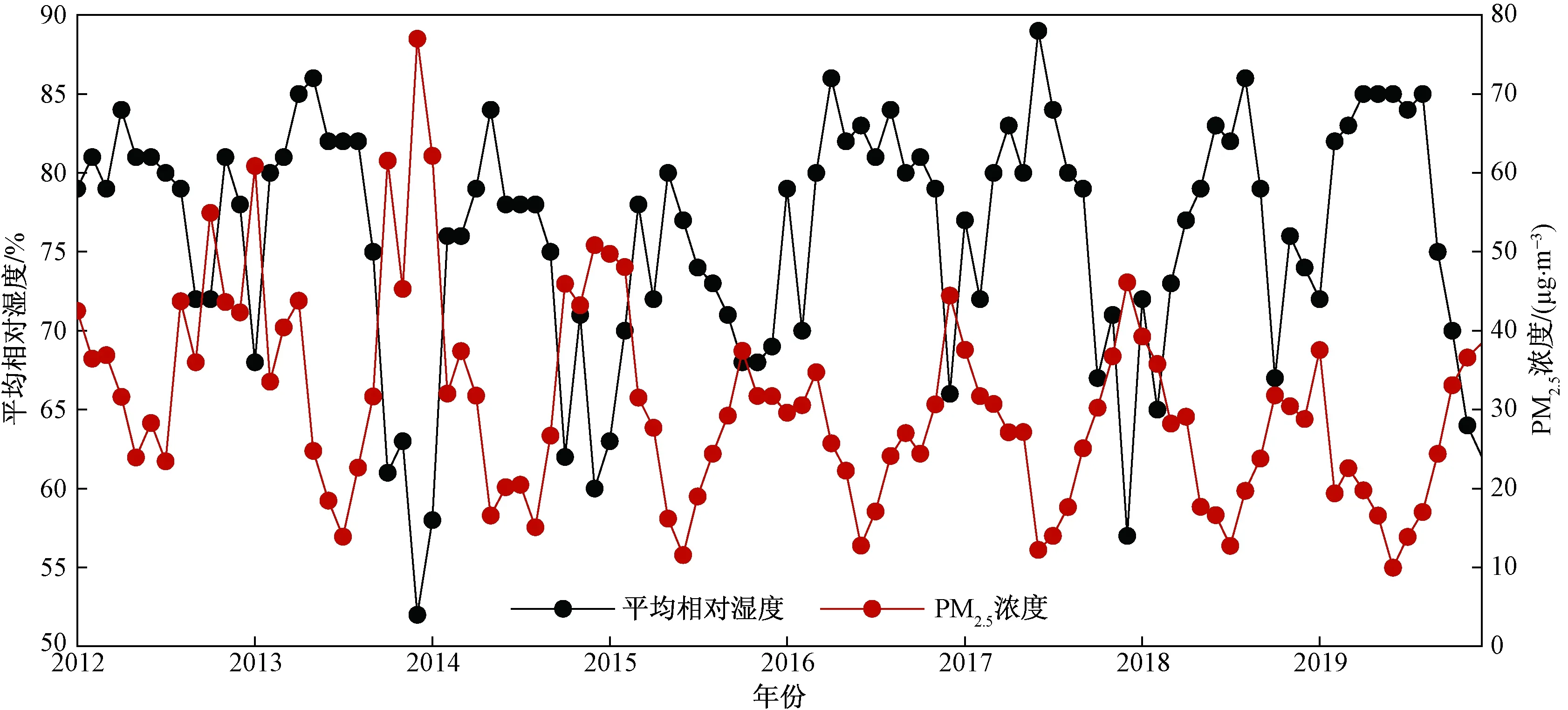
图8 2012—2019年月平均相对湿度以及月平均PM2.5浓度Fig.8 Monthly average relative humidity and monthly average PM2.5 concentration from 2012 to 2019

2.4 多元线性回归预测模型构建

由上述分析可知，月降水日数(x1)、月降雨量(x2)、偏北风频率(x3)、月平均相对湿度(x4)以及月平均温度(x5)均与月平均PM2.5浓度有显著的相关性，月平均风速与PM2.5的相关系数虽然不能通过显著性检验，但其本身对PM2.5浓度是存在一定影响的，因此将其设为x6。为了提高模型的拟合度，尝试将PM2.5浓度项加入模型中，把上个月的平均PM2.5浓度的观测值与往年同期的月平均PM2.5浓度的观测值的平均值设为x7。计算因变量的方差膨胀因子，结果表明变量之间不存在多重共线性，不影响方程的建立。

利用深圳市2012—2019年月平均PM2.5浓度数据以及气象因子数据进行多元线性回归分析，得到深圳市月平均PM2.5浓度的预测模型(变量选取情况如表1所示)，模型0:Y=51.146 3-0.618x1+0.010 4x2+0.239 9x3-0.598 2x4+0.710 2x5；模型1:Y=58.637 7-0.623 5x1+0.010 3x2+0.240 4x3-0.595 9x4+0.863 2x5-5.650 0x6。别对两个方程用F检验法进行方差分析(ANOVA)，得到判定系数：R02=0.79，R12=0.80；F统计量观测值分别为67.82、59.35，P分别为5.02×10-29、5.32×10-29。F检验的结果表示两个方程均能较好地对月平均PM2.5浓度进行拟合，但包含了月平均风速这一因变量的模型1拟合度更高，证明在气象因素对月平均PM2.5浓度的影响中，月平均风速有着不可忽视的作用，因此在模型的构建中月平均风速项应该保留。观察发现模型1方程中大多数变量的系数的正负号表示其与PM2.5浓度的相关性，但降水量的系数为正，经计算验证发现这是随着自变量数量增加导致的。用t检验法对模型1中单个变量系数的显著性进行检验，设显著性水平为α=0.05，降水量的系数没有通过检验，说明方程中降水量这一项对于月均PM2.5浓度的影响不如其他因子。

表1 模型变量选取情况Table 1 Selection of model variables

将6个气象因素以及PM2.5浓度项视为自变量，建立深圳市月平均PM2.5浓度的多元线性回归模型得到模型2:Y=93.437 7-0.257 6x1+0.02x2-4.255 6x3+0.015 2x4-0.816 8x5-0.331 3x6+0.445 8x7，F检验得到R22=0.818，F统计量观测值为45.83，P为9.50×10-25，方程通过F检验并且拟合度较好，初步认为模型2的模拟更接近实际观测值。值得注意的是模型2的拟合度比模型1的拟合度仅提高了0.018，说明气象因素仍然是影响PM2.5浓度的主要因素。对模型2的变量进行逐步t检验，将最不显著的因子剔除后重新检验其他因子，最终只有偏北风频率以及月平均相对湿度以及PM2.5浓度项被保留，表明在这一方程中，除了与自身高度相关的PM2.5浓度项外，偏北风频率以及月平均相对湿度是对月平均PM2.5浓度影响最大的气象因素。

计算得到模型1对2012—2019年以及模型2对2013—2019年的月平均PM2.5浓度的拟合值，如图9所示，自2014年起2个模型的拟合值均与观测值较为贴合，波峰与波谷出现时间的预测也较为准确，可较好地捕捉深圳月平均PM2.5浓度的季节性变化特征。为进一步比较两个模型的拟合效果，分别对2020年深圳月平均PM2.5浓度进行估计(图9)，发现模型1和模型2估计值变化趋势与观测值吻合度较高，相关系数分别为0.920与0.923，但数值都整体偏高，模型1估计值与实际观测值的平均绝对误差和平均相对误差分别为9.20 μg/m3、0.634，而模型2的分别为6.09 μg/m3、0.397，相比于模型1而言，模型2的预测准确度更高，再次证明了模型2更适合作为深圳月平均PM2.5浓度预报的参考。

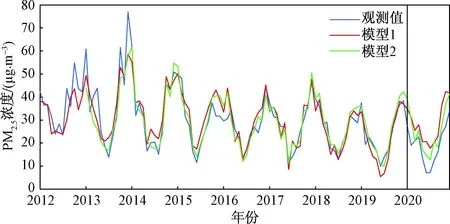
图9 月平均PM2.5浓度的观测值与模型1、模型2预测值对比Fig.9 Comparison of monthly average PM2.5 concentration between the observed value and the predicted value of model 1 and model 2

观测值与模型1预测值来自2012—2020年；模型2预测值来自2013—2020年；仅2012—2019年数据参与模型训练计算观测数据的月平均PM2.5浓度与上个月的差值，得到2020年2—11月的PM2.5浓度月际增量，同样地，计算得到模型2的PM2.5浓度预报值的月际增量。如图10所示，模型2的每月预报增量仅在3月、7月、9月与实际增量符号相反，说明模型2对于月尺度PM2.5浓度增减趋势的预报成功率达到了约73%。总体而言，利用6个气象因子与PM2.5浓度项建立的多元线性回归方程模型2可对深圳市月平均PM2.5浓度进行较好的拟合，虽模型2的R2比陈兵红等[32]建立的以日为单位的随机森林模型低0.016，但模型2在PM2.5浓度的季节性变化、每月增量的预测上有一定的表现，可以在月尺度上为大气污染防控上提供参考。

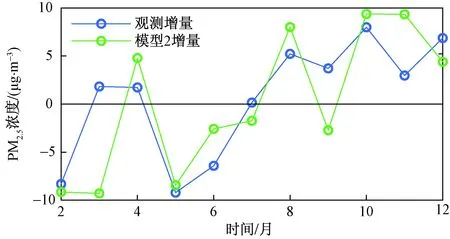
图10 2020年2—11月月平均PM2.5浓度观测值与模型2预测值每月增量Fig.10 Monthly increment of monthly average PM2.5 concentration observation and model 2 prediction from February to November in 2020

3 结论

基于2012—2019年深圳市PM2.5浓度月均值和月度气象监测公报数据，对深圳PM2.5浓度与月尺度气候要素的关系进行了系统研究，得到主要结论如下。

(1)从年际尺度和月际尺度观察，2012—2019年深圳市PM2.5浓度整体呈明显下降趋势，但在2013年有较大反弹，在2017年有较小反弹。PM2.5浓度与深圳灰霾日数均具有季节性特征：雨季(4—9月)PM2.5浓度以及灰霾日数较低，干季(1—3月、10—12月)较高。根据干季和雨季的日平均PM2.5浓度数据，发现干季PM2.5的污染情况改善比雨季明显，2013年PM2.5浓度的突变以及2017年的小幅增长均发生在干季。有效控制干季PM2.5浓度对于整体的大气污染防治有重要作用。

(2)深圳PM2.5浓度与多种气象要素均有关联。统计表明2012—2019年月平均风速与PM2.5浓度的相关系数参考意义不大，但对其影响不可忽略。深圳PM2.5浓度受区域输送的影响较大，从东北方向的输送可能是PM2.5浓度与月平均风速呈较弱正相关的主要原因，偏北风频率与PM2.5浓度也呈较好的正相关。平均温度与PM2.5浓度呈较好的负相关。降水对颗粒物的清除作用较好，降水日数、降水量与PM2.5浓度呈负相关。由于时间尺度不同，与前人研究结果相反，月平均相对湿度与PM2.5浓度呈现出显著的负相关，相关系数为-0.73，并且通过了显著性为0.01的检验。

(3)将上述气象因子作为自变量，建立关于月平均PM2.5浓度的多元线性回归方程得到模型1。经检验，月平均风速项对回归模型的建立有不可忽略的作用。将上个月与往年同期的PM2.5浓度平均值与往年同期的月平均PM2.5浓度的观测值取平均加入模型中，得到模型2的拟合度为0.818，比模型1的高，且对2020年的预测值更接近观测值，平均相对误差以及平均绝对误差大幅度减小，因而更适合作为实际预报的参考。并且模型2在月平均PM2.5浓度增减趋势的预报上有73%的准确率。研究得到的深圳月平均PM2.5浓度模型均对月平均PM2.5浓度整体的变化趋势拟合较好，尤其对季节性变化特征有较好的捕捉效果，但在某些时间段仍然会出现较大偏差，这可能是样本数据不够多导致的。