基于小面元配准的倾斜遥感图像拼接

2022-01-26岳广孙文邦李铜哨杨帅王国耀吴永康

科学技术与工程 2022年1期

岳广，孙文邦*，李铜哨，杨帅,2，王国耀,3，吴永康,4

(1.空军航空大学航空作战勤务学院，长春 130022；2.78102部队，成都 610000；3.95894部队，北京 100000；4.93787部队，北京 100000)

图像拼接技术是利用图像重叠区域进行配准形变后经融合处理后得到的一幅宽视野图像[1]。图像拼接最直接的优点在于增大了视野，然而受到成像器件的限制，单幅影像不足以满足视觉需要，多幅连续成像的方式成为较好的选择。为进一步增大图像视野，有时采用倾斜成像方式增大收容面积[2-3]。当倾斜成像分别从不同位置观察同一目标时，导致了相邻图像之间的重叠区域出现较大视差，给图像配准和拼接带来了难题。

为了解决倾斜图像拼接中的视差问题，许多具有代表性的方法被提出。Li等[4]构建稳健弹性形变模型，利用网格变换函数对图像进行形变，得到精确配准遥感图像，然而图像间匹配关系对拼接结果影响很大，配准结果过度依赖于特征点，该方法不能保证同一网格中的特征点位于同一平面，无法保证单应性矩阵的准确性，而导致拼接影像出现重影，视觉效果欠佳。贾贺林[5]将图像进行区域划分，由相似性原则对图像进行变换，保留了图像的原始信息，但是该法进行变换时引起了非重叠区域失真，对于图像视差问题也未能很好地解决。刘强等[6]将图像划分为多个图像块，建立网格优化模型，将直线结构约束整合于NISwGSP算法，有效矫正了扭曲图像的失真，提高了拼接自然度，但对于畸变校正程度较小，适用范围不高。王红君等[7]利用改进定向快速旋转(oriented FAST and rotated BRIEF，ORB)算法提升了拼接图像匹配的速度与精度，但对于图像视差问题考虑较少，容易出现拼接重影问题。Yuan等[8-9]提出了一种基于超像素的最佳拼接缝搜索方法。通过改进能量优化函数，将图像纹理、梯度等信息同时整合，经图割算法求解后，能有效找到一条纹理复杂度低，边缘信息突出的拼接线。但该方法以灰度和结构作为考量，刻意避开了某些区域，可能导致重点目标的损失。

针对于上述遥感影像拼接的问题，既要提高图像配准精度，又要保证重叠区域目标不丢失且拼接不出现重影，现提出一种针对航空倾斜图像拼接的方法。首先采用全局变换矩阵提取图像重叠区域，构建重叠区域Delaunay三角网并完成基于三角网的图像配准，最后结合渐出渐入式融合进行拼接缝过渡。

1 基于小面元配准的倾斜图像拼接

倾斜成像时将导致像点位移，同时重叠区域产生出现了视差。采用全局转换矩阵，通过计算可提取图像重叠区域。在重叠区域中利用特征匹配对构建重叠区域Delaunay三角网并对相应三角网逐个进行仿射变换与差值，即可提高图像配准精度。利用渐出渐入式融合，消除图像融合带来的重影，提高图像目视效果。

1.1 倾斜成像引起像点位移

进行倾斜成像时，有效地增大了图像视野，使得单次成像获得了更多地理信息，与此同时，也引起了图像的像点位移。图1所示为倾斜成像示意图。成像区域为具有地形起伏的丘陵地带，从点S1和S2对山顶进行观测，分别得到对应地面点坐标S′1和S′2。由于地形起伏遮挡，成像倾斜角不同，对地观测到的范围以及变形程度也不同，即发生了像点位移，同时重叠区域产生出现了视差。相比于垂直成像，倾斜成像时地形起伏带来的像点位移影响更大，给后续图像配准带来了难题。

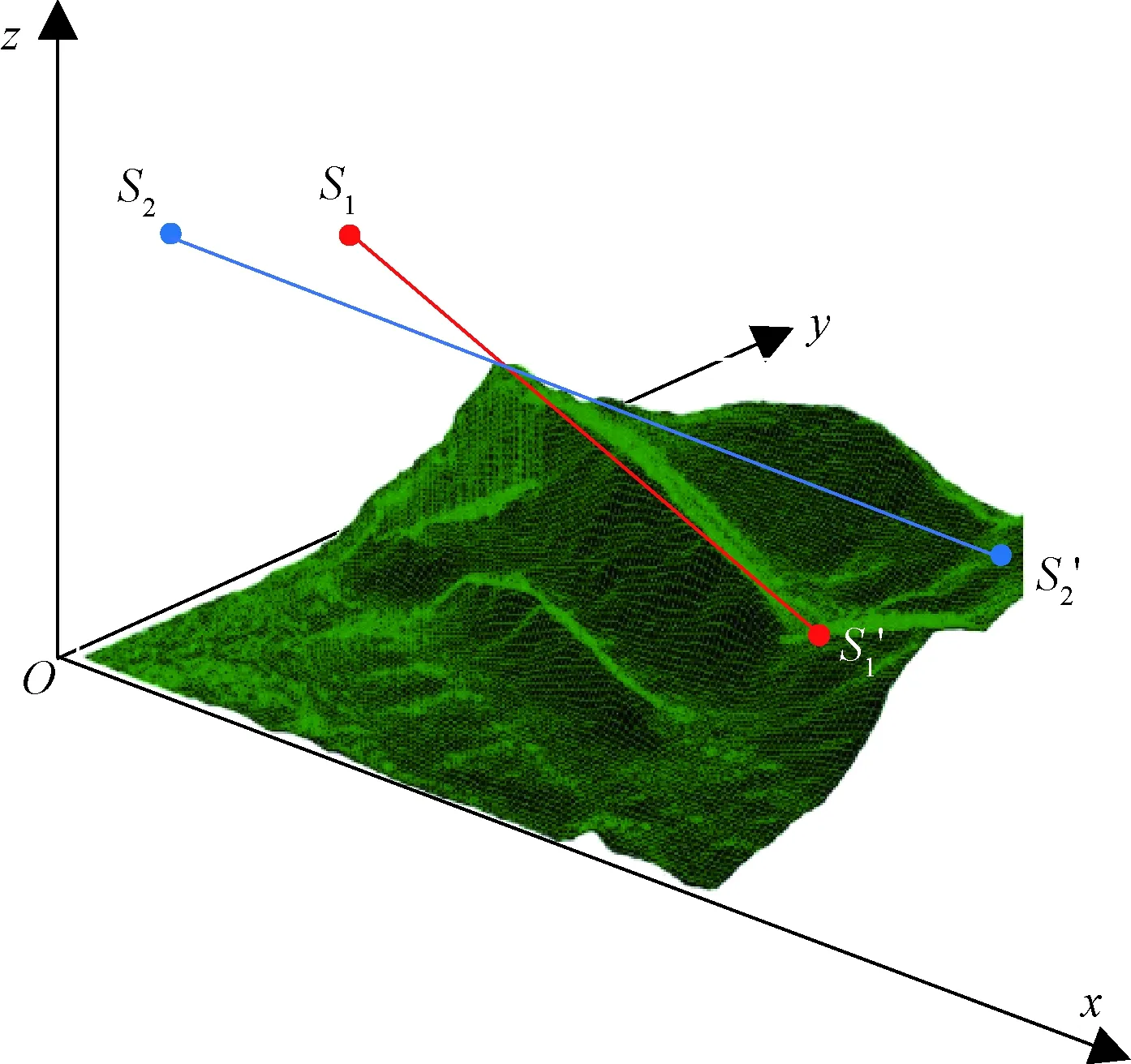
图1 倾斜成像示意图Fig.1 Schematic diagram of tilt imaging

1.2 重叠区域提取

由于图像重叠区域存在视差，图像中部分区域出现配准误差。通过重叠区域提取，针对重叠区域进行精细配准，能进一步提高配准精度。

设I1、I2分别为基准图像与待配准图像，大小为M×N。经特征匹配对间的映射关系，求解得到转换矩阵H，利用该转换矩阵，可实现图像配准预对齐。图2所示为经特征匹配后预对齐图像。I′2为I2经单应性变换后图像。O-cr为数字图像显示坐标系统。

图2 图像预对齐Fig.2 Image pre-alignment

由点x1、x2、x3、x4所围成区域即为配准重叠区域。通过求解四点坐标，即求得图像重叠区域。四点坐标可由式(1)求解，即

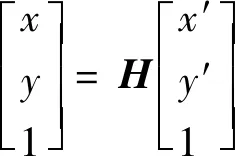
(1)

式(1)中:(x，y)为预对齐后坐标；(x′，y′)为图像原坐标；转换矩阵H中8个参数经特征匹配求解单应性矩阵后为已知。

(2)

点x1为I2顶点坐标，在数字图像显示坐标系统中一般可记为(1，1)，经单应性变换后求得。通过式(1)，即可求得x1当前坐标。

点x2为I′2与I1的交点。其中，x2的r坐标已知，记为N，且对应x′2的c坐标已知，记为1。将各已知量代入式(1)，求解得x2。同理，x4的c坐标已知，记为M，且对应x′4的r坐标已知，记为1，求解得x2。

点x3坐标为图像显示系统中图像顶点坐标。

1.3 利用三角网进行小面元配准

由于构建Delaunay三角网对特征匹配对要求精度高，当出现特征点对误匹配现象时，将导致构建三角网出现错误，无法进行后续配准。因此首先进行误匹配对剔除，采用RANSAC算法可剔除重叠区域特征误匹配对，设置迭代次数为500，模型阈值为0.05。

采用文献[10]中三角网快速合成法，利用特征点构建Delaunay三角网。利用若干圆弧进行离散区域弧带划分，设置弧带搜索规则，即构建三角网过程中仅在当前弧带搜索并完成构建，当前弧带搜索完毕才可进入下一弧带，往复循环即完成三角网构建。

一只大象朝着四人走来，大象一点儿也不怕人，它身后还跟着几只小象。大象一家走到河边饮水，河边有个古老的石牌，上面写着—泿水。

利用倾斜遥感成像时，由于对地观测的角度方位不同，图像发生不同程度变形。通过对重叠区域进行三角网划分，利用三角网间仿射变换能有效完成三角网间配准。图3所示为三角网逐个配准示意图。

图3 三角网配准Fig.3 Triangulation registration

利用待配准单个三角网三顶点位置坐标与相对应的基准图像三角网顶点坐标求解单应性矩阵H各参数，公式为

(3)

计算可得到对应点间仿射变换关系，利用最近邻差值即实现待配准三角网向基准三角网的配准。对待配准区域三角网逐个进行仿射变换及差值，即完成全域待配准图像向基准图像配准。

1.4 图像融合

为了消除图像拼接重影，需要对配准后图像进行融合。直接融合是最简单的融合方法，但实际效果并不好，经直接融合后的图像目视效果较差，容易出现重影，拼接缝非常明显。采用渐出渐入式融合，渐出渐入式融合是基于直接融合改进而来。相比于直接融合，渐出渐入式融合采用求取重叠区域像素平均值的方法求取像素的加权平均值。图像渐出渐入式融合可以用式(4)表示为

(4)

式(4)中：f(x，y)为待拼接图像；g(x，y)为参考图像；ωf、ωg为权重值。

(5)

通过引入权重系数，对于重叠区域位置不同，利用权重之间的差异进行图像融合，有效实现重叠区域的过渡，融合效果较好。

2 图像质量评价

图像质量评价是通过一定的方法手段对图像效果进行量化的分析和评比。图像质量评价包含主观评价和客观评价。通常主观评价占主导地位，依靠个人的主观感受对图像质量进行评价。但是由于个人主观感受缺乏量化指标，无法更客观准确地反映图像质量。因此结合客观与主观评价进行综合评价。

2.1 主观评价

主观评价标准采用国际无线电咨询委员会制定的CCIR500-1的主观评价标准[11]，如表1所示。

表1 主观评价标准Table 1 Subjective evaluation criteria

2.2 客观评价

2.2.1 峰值信噪比

峰值信噪比(peak signal-to-noise ratio，PSNR)评价是利用图像间像素差作为评价指标的质量评价方法。PSNR取值范围为(0，+∞)。评价值越大，表示图像质量越高。该算法通过计算图像均方误差MSE，然后利用式(6)计算得到该评价值。

(6)

(7)

式中：I(i，j)、K(i，j)为大小为M×N的图像；n为图像位深，取值为8。

2.2.2 结构相似性

结构相似性(structural similarity index，SSIM)评价分别从亮度、对比度和结构3个方面评价图像相似性。SSIM取值范围为[0，1]。评价值越大，表示图像的相似性越高。SSIM方法函数表示为

SSIM(x,y)=[l(x,y)]a[c(x,y)]β[s(x,y)]γ

(8)

(9)

(10)

(11)

(12)

式中：x、y分别为参考图像和待评价图像；μx、μy、σx2、σx2、σxy分别为图像x、y的均值、方差和协方差；C1、C2、C3是常量，利用参数α、β、γ调整函数中3个方面所占的比重。

SSIM进行评价时，结构为主要影响因素，当α=β=γ=1且C3=C2/2时，得

(13)

3 实验与分析

实验采用航空倾斜面阵图像进行配准与拼接实验，如图4所示。图像大小为3 600×3 600像素。

图4 实验图像Fig.4 Experimental images

为了验证本文算法配准精度高的优点，采用对比验证。首先给出图像配准后特征点分布情况，如图5所示。图中蓝色点表示原图像特征点分布情况，红色点表示配准后特征点分布情况。

图5 特征点分布对比Fig.5 Feature points distribution

全局转换矩阵配准结果如图5(a)所示，通过观察细节部分可以发现，红蓝特征匹配对出现很大位置偏差，仅仅依靠全局转换矩阵实现倾斜图像配准较困难，配准精度不高，效果不佳。APAP(as-projective-as-possible image stitching)、AANAP(adaptive as-natural-as-possible image stitching)实验结果分别如图5(b)、图5(c)所示，通过观察特征点分布情况，发现特征点对间坐标偏差较大。通过对待配准图像进行网格划分，进行网格变换的方式完成的图像配准，过度依赖特征点，当网格区域不存在特征点或者存在少量特征点时，该网格配准效果不佳。实验结果如图5(d)所示，通过观察可以发现，原图像特征点分布与配准后特征点分布基本重合，红色特征点基本对蓝色特征点实现覆盖，特征点间坐标偏差较小。由于采用了小面元纠正的方法，使得重叠区域部分目标得到了充分匹配，通过进行三角网间的仿射变换及插值，完成了高精度的图像配准。由倾斜成像过程中带来的图像视差，基本上能够被消除。

特征对间的均方误差如表2所示。通过表2数据，对本文算法所得结果求得均方误差，该值明显小于APAP算法，说明了依据本算法法所得结果特征点对间差值小，证明本文方法所得结果配准效果更好。

表2 特征对间的均方误差Table 2 Mean square error between feature pairs

为了验证本文算法拼接效果好的优点，给出全局转换变换、APAP、AANAP和本文算法结果，如图6所示。

图6 图像拼接结果对比Fig.6 Comparison of image stitching results

主观评价方面。全局转换矩阵配准结果如图6(a)所示，通过观察细节部分可以发现，拼接图像出现重影，图像拼接效果不佳，视觉效果不佳。APAP算法结果如图6(b)所示。经APAP算法配准后图像特征点间出现偏差，经图像融合后，一定程度上减弱了坐标偏差带来的影响，但是这种方式并不能消除重影。观察细节部分(APAP蓝色框中)可以发现，在图像灰度差异较大的区域，出现了明显重影，严重影响了目视观察，降低了视觉效果。AANAP算法结果如图6(c)所示，经采用局部变换与全局变换加权的方法实现图像拼接，视觉效果较好，但图中细节(AANAP橙色框中)出现了错位现象，降低了图像评价质量。本文算法拼接结果如图6(d)所示，对比本文算法细节部分，重叠区域基本实现完全对齐，未发现有明显重影，图像重叠区域与非重叠区域实现了良好过渡，图像拼接效果较好。依据CCIR500-1的评价准则，可以确定本文拼接效果评分位于4～5。

客观评价方面。采用PSNR和SSIM算法对文献全局转换方法、APAP、AANAP和本文算法进行图像质量评价，评价结果如表3所示。

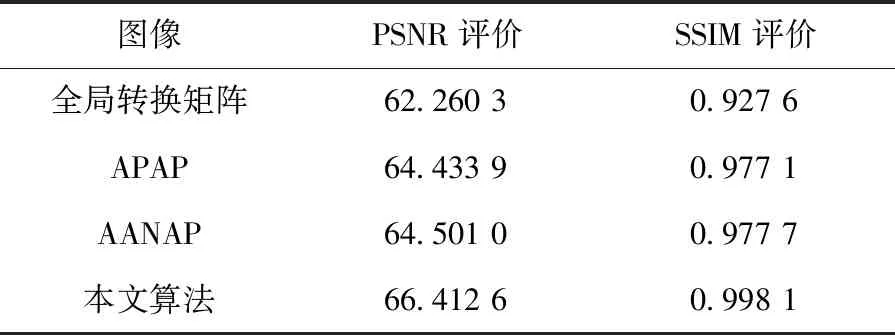
表3 评价结果Table 3 Evaluation results

通过对比评价得分可以发现。PSNR评价与SSIM评价结果优劣情况基本保持一致。全局转换矩阵方法拼接两项评价得分均为最低，明显差于其他方法评价得分。本文算法得分较优于其他算法，这是由于本文算法配准精度高，没有明显的配准错位，在图像融合中，有效消除了图像拼接的重影。从而验证了本文算法拼接精度好、拼接效果好的优点。