基于多目标遗传算法的多配置风电机组控制
2022-01-26常国锋
常国锋
(新乡学院计算机与信息工程学院,新乡 453003)
太阳能、风力等间歇性能源(intermittent energy,IE)已被纳入电力系统中,改变了发电、输电和配电的规划和运行[1]。因此,电力系统环境发生了重大变化,需要关注智能化的优化方法,充分发挥可再生能源在电力系统工程中的作用。
实现电力系统的最优运行规划不但有利于电力企业和运营商,还能够提高电网用户满意度。由于可再生发电机组通常可安装在用电负荷附近,因此引入此类电力资源,有利于技术、环境和经济等各方面的发展。进一步促进了环境友好的发电、输电和配电系统的进一步开发[2]。
从经济角度来看,在电网中集成能够储存的可再生能源,可以减少电力分销商对上游电企的依赖程度,销售储备能源,并利用发电点与用电点距离较近的优势减少损耗,由此提高分销商的效益[3]。然而,为了将间歇性能源集成到配电网络中,需要进行大量的研究,以鲁棒的方法论为基础,采用适当的控制和储能设备。文献[4]提出一种基于虚拟定子电压定向的新型双馈风机控制策略,可动态地调节风力机组的输出,以响应电网频率的变化。文献[5]提出一种基于数据驱动的多风电机组协同控制方法,在风电场层通过粒子群算法在线求解多风电机组协同控制功率优化指令,实现风电场整体发电功率的优化。
此外,文献[6]介绍了直驱式风电机组的虚拟同步发电机实验系统及控制策略,风电机组的虚拟同步发电机功能要求机组有功功率响应于电网频率变化率及变化量。但未考虑步进式电压调整器(step voltage regulator,SVR)的使用及其影响。文献[7]开发了控制风电能源的复杂配电网络,提出一种风电机组状态检测和评估方法。采用贝叶斯优化算法优化超参数,但在分析中没有结合现实配电网络。文献[8]考虑负荷波动、风电有功输出的随机性,提出一种高风电渗透率下变速风电机组参数系统频率调整的优化控制策略,考虑使用电容器组、SVR的多种组合的多目标配置和分析。
研究者从技术、经济和环境等角度出发,在该领域进行了大量研究,针对各种目标和约束,开发了不同的设备和方法。但SVR、电容器、风力和电池储能系统(battery energy storage system,BESS)的多配置优化较少研究。因此,现提出一种多目标遗传算法(epsilon multi-objective genetic algorithm,ε-MGA),优化方法实施于3个不同的配置上,并通过所有配置之间的比较,验证最适用于复杂配电网络的配置。
1 模型描述
提出的方法实施在20 kV中压配电系统,包含162母线和165条线路,以及负责电力的传输、分配和消耗的变电站、配电站(distribution station,DS)和变电所(transformer substation,TS)所组成的配电网络。
1.1 风电和储能系统
集中式风电站和电池储能系统(BESS)分别被考虑为IE和储能系统(energy storage system,ESS)。将变电站连接至中压主TS或负荷母线的中央母线DS,是风电站和BESS的可行设置位置。通过DS可输送更多电力,而且是降低当前配电网络中功率损失的最佳选项。此外,当风力发电机组的生产容量超过网络的负荷需求时,可以将额外电力传输并储存在BESS,减少能源浪费。优化方法中考虑的风力发电机在额定风速下的最大输出功率为0.5 MW。
假定当前配电网络中使用双向的BESS,优化的目的是确定BBS充放电时间的最优调度。根据文献[9],为电力系统操作人员定义3种不同的控制策略。第一种策略中,每当指定比例的风力发电量和风电机组输出功率高于负荷水平,则运行ESS以满足储能需求。第二种策略中,每当负荷需求高于指定比例的风力发电量,可使用ESS以满足负荷需求。第三种策略中,当可用发电量不能满足负荷需求,则使用ESS。提出的方法论中使用了第三种策略。
BESS在时间t的充放电调度和荷电状态(state of charge,SOC)及其约束的数学表达式为
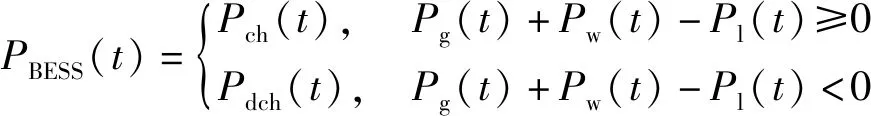
(1)
式(1)中:Pch、Pdch、Pg、Pw和Pl分别为配电网络在时间t处的BESS充电时间、放电时间、上游电力、风电场发电和负荷需求。
SOC(t+1)
(2)
式(2)中:SOC(t+1)和SOC(t)分别为时间t+1处和t处的BESS荷电状态。
由式(2)可知,当总发电量超过需求负荷时,BESS开始运行在充电模式,由此SOC会增加。相反,当需求负荷大于供电总量时,BBC会在放电模式下作为发电机运行。BESS在充放电和SOC方面受到以下约束:
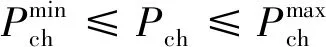
(3)
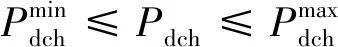
(4)
SOCmin≤SOC(t)≤SOCmax
(5)
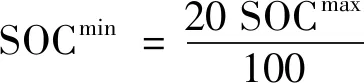
(6)

1.2 电容器组和步进式电压调整器
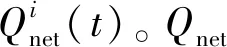
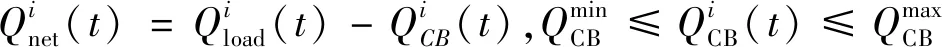
(7)
同样,SVR作为一种分布式电压调整设备,被广泛用于配电网络中。SVR的工作原理基于嵌入式自耦变压器和调压操作。通过对自耦变压器绕组上的抽头进行切换,可实现在切换操作确定范围内的电压调整。标准SVR包含电压调整范围10%上下的换向开关[10]。考虑带有32个切换步长的SVR,其中包含电压调整器(voltage regulator,VR)范围内的16个加压步进(正值)和16个降压步进(负值)。每个步进意味着其操作中0.625%的电压变化。
2 提出的控制优化方法
基于电力潮流的大规模复杂配电网络的实时优化是较为困难的任务。在这种复杂电力网络中加入多个设备以进行规模和布局优化,会进一步增加决策变量的数量和优化复杂度,但可以得到可行的收敛解。此外,内存要求和仿真时间都会非常高。为此,利用ε-MOGA,并结合NR电力潮流分析,提出了鲁棒的实时优化方法,以得到最优解。
图1所示为所提方法的各阶段流程图。
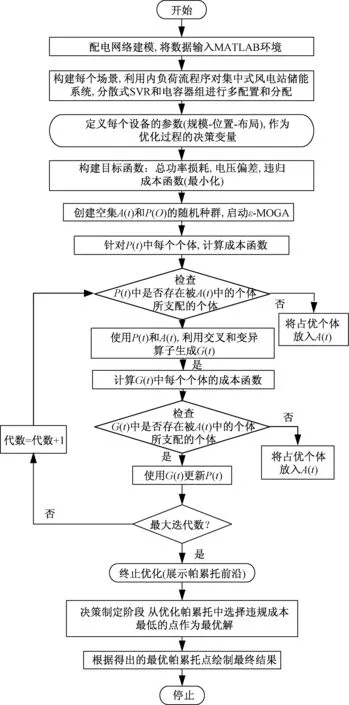
图1 提出方法的流程图Fig.1 Flow chart of proposed method
2.1 ε-MOGA的理论概念
2.1.1 概念定义
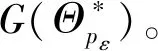

(8)
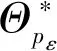
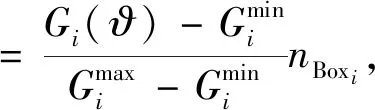
∀i∈[1,2,…,n]
(9)
当且仅当式(10)对于box(ϑ)={box1(ϑ),box2(ϑ),…,boxs(ϑ)}成立时,数值为G(ϑ1)的解ϑ1比数值为G(ϑ2)的解ϑ2具有ε优势,即
[Box(ϑ1)Box(ϑ2)]∨[Box(ϑ1)
=Box(ϑ2),ϑ1ϑ2]
(10)
Box(ϑ1)≠Box(ϑ2)∧Box(ϑ1)≻εBox(ϑ2)
(11)
相应的,利用无公共子空间的ε-占优解,对A(t)进行更新。使用智能化的分布使得在一个子空间的两个ε-占优解之间,选择与子空间的中心距离更近的解,并避免占优解属于相邻的子空间[13]。
2.1.2 种群分类
该算法中定义了3种类型的种群。
(1)P(t)。种群大小为NP,被视为主种群,在每次迭代过程中对搜索空间D进行探索。
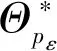

(12)
式(12)中:nBoxmax为子空间最大数量。
(3)G(t)。种群大小为偶数NG,被称为附属种群。使用变异概率和交叉比,在种群P(t)和A(t)上执行交叉算子和变异算子,以得到种群G(t)。
2.1.3 优化算法步骤
步骤1提出的优化算法的主要步骤如下。
建立一个空种群A(t),以启动算法。
步骤2创建随机生成的P(t),其中包含来自初始化搜索空间D的Np个个体。
步骤3针对P(t)的每个个体进行目标函数评价。
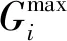
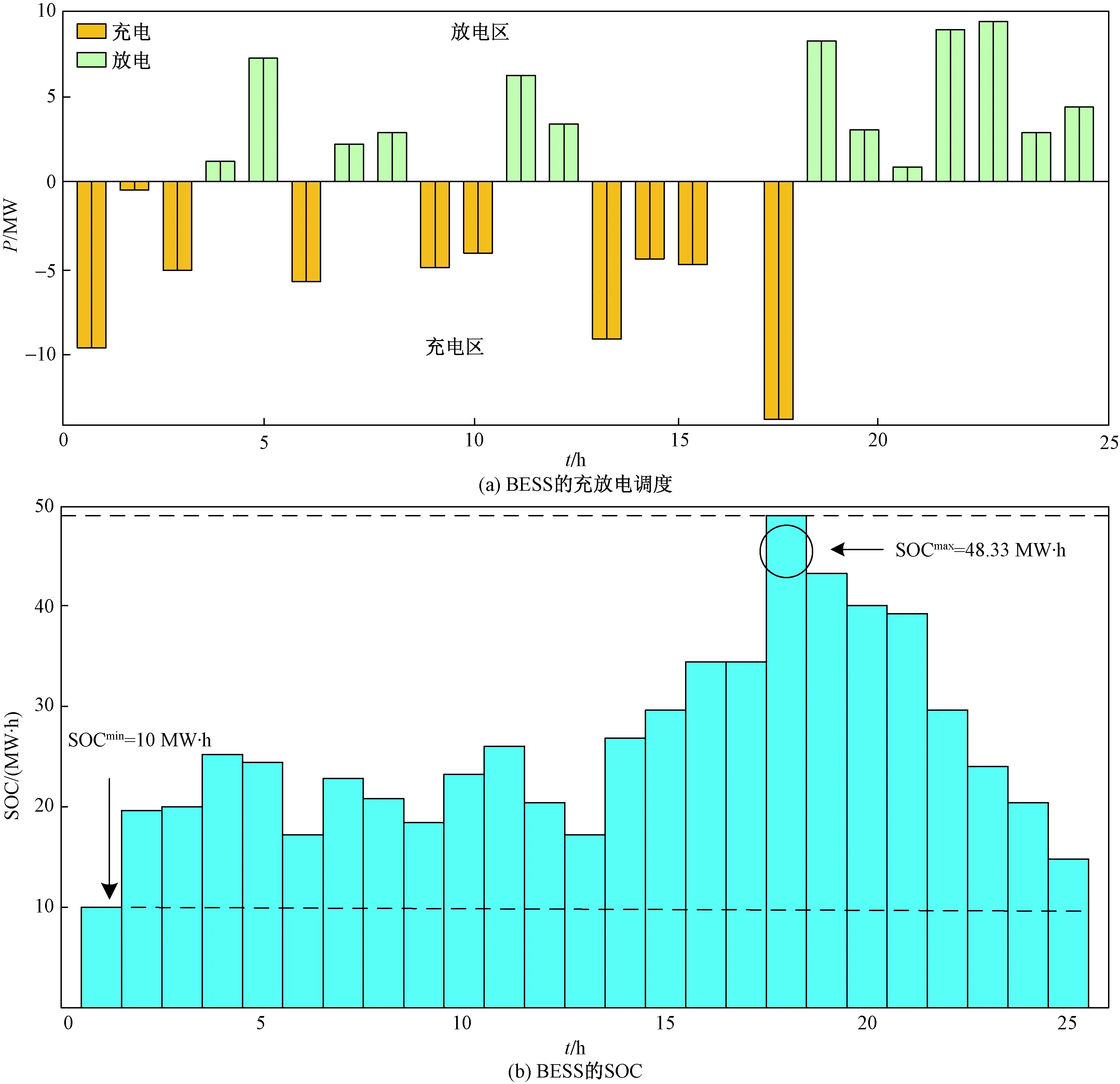
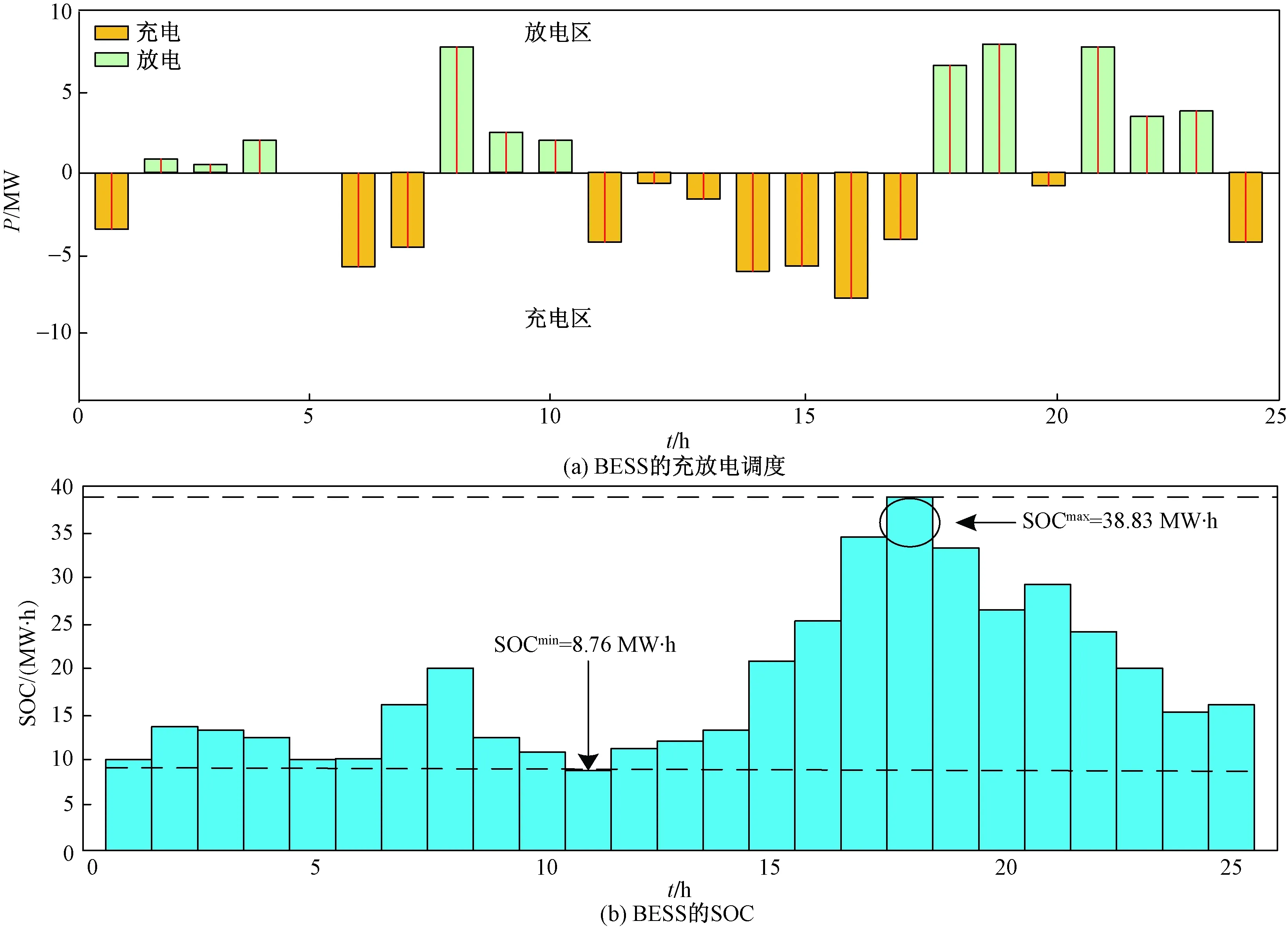
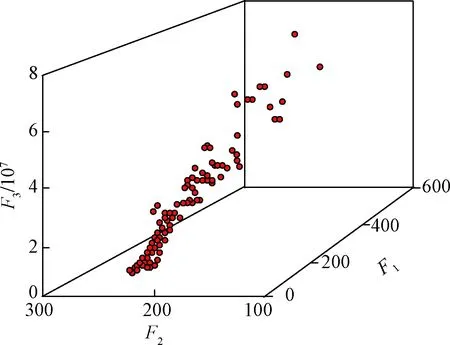
步骤5按如下方法创建附属种群G(t)。①从P(t)和A(t)中分别随机选出两个个体 ϑP和ϑA;②生成一个随机数μ∈[0,1];③若μ>Pc/m(交叉/变异概率),则通过扩展线性重组技术对ϑP和ϑA进行交叉;④若μ 步骤6针对G(t)中的每个个体进行目标函数的评估。 步骤7根据其在目标空间中的位置,对A(t)中来自G(t)的个体进行分析和放置。 步骤8利用G(t)中的个体对P(t)进行更新,以使得P(t)中的随机个体ϑP被替换为G(t)中的个体ϑG,其中ϑP仅被ϑG支配。 选择准确度最高的功率流分析方法牛顿-拉夫逊(Newton Raphson,NR)[14],以执行电力潮流分析。在此基础上,提出了一种改进的NR电力潮流方法。在分析和论证可再生能源、ESS和调整设备对网络参数和指标的影响上,电力潮流分析发挥着重要作用。 2.2.1 功率平衡约束 常规稳态AC功率流约束网络是每个母线处非线性方程式的集合,公式为 (13) 式(13)中:Pi和Qi分别为母线i处的净有功功率和净无功功率;n为母线数量;Vi为母线i处的电压幅值;Vj为母线j处的电压幅值;Gij和Bij分别为第i个母线和第j个母线之间的电导和电纳;θi和θj分别为母线i和母线j处的电压角[15-16]。 2.2.2 母线电压约束 网络的母线电压幅值和相角的最大值和最小值限制可表示为 (14) (15) 2.2.3 支路电流约束 使用线路电流约束,以确保电流不会接近发热极限。其能够将线路传输和接收末端的电流保持在线路上限之内,即 (16) (17) 在优化问题中,为得到良好的解,目标函数的选择至关重要。优化方法旨在实现包含3个成本函数的目标函数最小化,这3个成本函数彼此存在权衡关系。第一个目标函数为系统的总实际功率损耗,第二个目标函数为每日电压偏差,公式为 (18) 式(18)中:k为支路数量;Zk为k条分支的阻抗;ilk为通过k条支路的电流。 (19) 式(19)中:m为支路编号;Vm为母线m处的电压;Vsp为规定电压。 最后,第三个目标函数空间专门针对违规成本,包含4项重要的优化和电力潮流约束。最后一个目标函数F3可表示为 (20) 式(20)中:Violp为违反了定义的约束项p;βp为违反了约束项p的惩罚因数。 由此,推导出4个约束项的违规成本为 (21) (22) (23) (24) 在第3个目标函数中,考虑到特定约束的违反情况,原因如下:①给予约束更大的优先度;②提高算法得到自然可行解的鲁棒性;③在潮流分析中防止雅可比矩阵的奇异性。 仿真通过创建ESS、SVR和CB的多种配置,实现3种独立的优化场景。 该场景配置了集中式BESS和风电站,以展示将两者集成到现实配电网络时的影响。优化过程中,首先对BESS和风力发电机进行建模和数学表示,得出优化规模(最优帕累托前沿)如图2所示。集中式BESS和风电站场景的优化结果如图3所示,其中图3(a)是BESS的充放电调度;图3(b)是BESS的SOC。 图2 集中式BESS和风电站场景的最优帕累托前沿Fig.2 Optimal Pareto frontier for the centralized BESS and wind power station scenarios 图3 集中式BESS和风电站场景的优化结果Fig.3 Optimization results of centralized BESS and wind power station scenarios 在配电网络中模拟BESS和SVR两种设备场景,以分析BESS和SVR两种设备同时运行时的影响以及风电站最优穿透。得出的最优帕累托前沿如图4所示。BESS和SVR两种设备场景的优化结果:BESS的最优参数,如图5所示,其中图5(a)是BESS的充放电调度;图5(b)是BESS的SOC。 图4 BESS和SVR两种设备场景的最优帕累托前沿Fig.4 Optimal Pareto frontier for two device scenarios,BESS and SVR 图5 BESS和SVR两种设备场景的优化结果Fig.5 Optimization results for two device scenarios,BESS and SVR 该场景是对集中式BESS、风电站、SVR和CB共同进行优化,观察这些设备组合对配电网络参数的影响。图6和图7展示了该场景的优化和仿真结果。 图6 集中式BESS、风电站、SVR和CB场景的最优帕累托前沿Fig.6 The optimal Pareto frontier for the centralized BESS,wind power station,SVR and CB scenarios 图7 集中式BESS、风电站、SVR和CB场景的优化结果Fig.7 Optimization results for the centralized BESS,wind power station,SVR and CB scenarios 在执行优化前,先进行基准案例,即典型电力短缺场景的仿真。在基准场景中得到的结果为:最小电压0.835 pu,配电网络总损耗148.79 MW。这种情况下,网络的操作会不可避免地趋向断电和负荷减少,造成电力系统设备损坏或使用寿命减少,并导致向终端用户的供电不足。该案例被视为100%依赖于上游电力,日耗电量为1 696.7 MW·h(表1)。 在集中式风电站和BESS场景中,使用提出的技术,仅对集中式风电站和BESS进行控制优化配置。表1、图2和图3给出了仿真结果,其中风力发电机的最优数量为141台,功率损耗节约46%,降低电压偏差60%,且最小电压提升0.9 pu。但该场景中,BESS的最大容量设定为超过48 MW·h,这要求较大的经济投入。因此,更倾向于逆电力潮流。 表1 多目标多配置的控制优化结果Table 1 Control optimization results for multi-target and multiple configurations BESS和SVR两种设备场景中对SVR、BESS和风电站进行优化后,网络的最小电压上升,对上游电力的依赖减少60%。总功率损耗并未发生变化。 集中式BESS、风电站、SVR和CB场景在控制优化部署中同时考虑所有设备。该场景中,系统最小电压为0.901 MW,总功率损失为94 MW。同时,SVR最优数量为8个,CB最优注入无功功率为4.84 Mvar,风力发电机最优数量为120台,BESS最低优化容量为33.66 MW·h,日常对主电网的依赖降至43.46%。 除了通过仿真结果验证SVR、CB、风电和BBS的影响之外,还针对SVR开发了一个新的指标,以评估SVR的切换操作在相关场景中的影响,表2给出了所有相关场景中得出的设备数字关联支持指数(digital standard systems interconnect,DSSI),DSSI指在两个相邻接的数字配线架或其等效设备之间,对规定速率的数字信号进行数字传输的全部手段。可以看出集中式BESS、风电站、SVR和CB的DSSI指标最好。 表2 不同场景中的SVR每日切换指标Table 2 SVR daily switching metrics in different scenarios 开发了无功功率补偿器、电压调整器、存储系统和间歇性风电的最优控制方法,提出了基于多目标遗传算法的控制优化方法。仿真实验通过在162节点的现实配电网络中接入或移除不同设备实现多个不同配置,以执行提出的优化方法。同时,详细分析了每种配置的有效性,输出结果证明了提出的方法论的优越性。所提方法可以应用到与配电网络相关的控制优化算法中。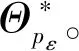
2.2 电力潮流分析和约束

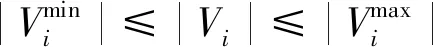


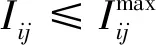
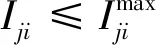
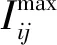
2.3 目标函数设计
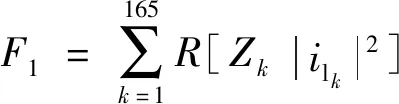
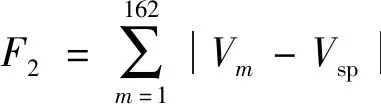



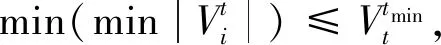


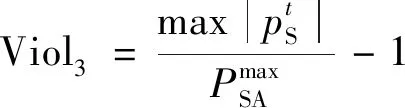



3 实验仿真与分析
3.1 集中式BESS和风电站场景

3.2 BESS和SVR两种设备场景

3.3 集中式BESS、风电站、SVR和CB场景
3.4 分析

5 结论
