弱电网条件下并网逆变器阻抗协同稳定域辨识

2022-01-26郭志华薛晓慧厉娜孟祥甫马晓琴

科学技术与工程 2022年1期

郭志华，薛晓慧，厉娜，孟祥甫，马晓琴

(国网青海省电力公司，西宁 810008)

目前，大量的可再生分布式发电(distributed generation，DG)接入弱电网，实现了零燃料成本、最小运行成本和零污染，但是这种弱电网在电磁时间尺度上容易发生低频振荡和谐波振荡[1]。因此针对并网逆变器在弱电网下的低频谐波振荡研究得到了广泛的关注。

一方面，状态空间方法被广泛地应用于电力电子变换器控制的电力系统的小信号稳定性分析。文献[2]提出了一种基于状态空间模型的无电压/电流双闭环控制器的并联变换器小信号稳定方法。文献[3]进一步提出了降速控制变换器和P&Q控制变换器的全阶状态空间模型。为了得到各参数的稳定空间，提出了基于守护映射理论的状态空间稳定域方法[4]。随着网络规模的扩大，计算复杂度急剧增加。因此，提出了几种降阶方法，如Kronreduction方法[5]、扰动方法[6]、基于Gramian的降阶方法[7]等。然而，建立复杂系统的整个小信号状态空间模型仍然很困难，因此，基于阻抗的方法被广泛应用于电力系统稳定性评估。

Middlebrook首次提出了基于阻抗的方法，并基于源输出阻抗和负载输入阻抗之间的返回比矩阵来分析由电力电子变换器控制的电力系统的稳定性[8]。文献[9]通过广义奈奎斯特准则(generate nyquist criterion,GNC)来评估小干扰稳定性，文献[10]提出逆Nyquist稳定性判据来保证忽略了变换器输出阻抗原点和右半平面的极点。考虑到镜频耦合特性，分别提出了基于视阻抗分析和基于谐波传递函数的阻抗法。为了消除复杂的GNC过程，降低计算复杂度，研究了修正稳定性准则和稳定性禁区准则两种方法。然而，基于经典阻抗的方法更注重线路阻抗稳定点的辨识和回路比矩阵的稳定域，不能提供系统参数的稳定域。虽然经典的基于阻抗的方法没有提供小信号稳定工作的协同区域，但是基于GNC的逐点阻抗法可能是获得小信号稳定域边界的一种方法。然而，需要绘制数千条广义奈奎斯特曲线，工作量巨大。另外，逐点法可以从数值模拟中得到小干扰稳定区的边界。这种方法的精确度相对来说较高，但是计算速度非常慢。特别是当系统中存在多个网格时，很难获得稳定区域。

针对上述问题，现提出一种弱电网条件下并网逆变器在线阻抗协同稳定域辨识方法,通过实验验证提出方法的有效性，为系统规划和稳定方法的研究提供参考。

1 并联电网逆变器的弱电网终端阻抗矩阵

由N个网络和弱网格组成的弱电网如图1所示。其中，该结构将随设定的网格数目而改变。在实际应用中，弱电网是一个由大量同步发电机以及基于变流器的分布式资源、储能和负荷组成的复杂系统。对所有弱电网中的设备进行建模是不现实的，为了解决这一问题并从稳定性角度来评估这个复杂系统，短路比(short circuit ratio,SCR)已被广泛应用到现有的研究中。将SCR定义为SCR=SSC/SN，其中SSC是公共耦合点(point of common coupling,PCC)的短路容量，SN是并网设备的额定容量。一般来说，当SCR低于6时，电网强度较薄弱。从实际应用的角度看，在感应线路系统中，SCR可以近似表示为SCR=1/Lg，在电阻线路系统中，SCR=1/Rg，Lg和Rg分别表示等效电路的电感和电阻。其中，随着阻抗的增加，SCR变小，从而导致电网强度减弱。综上所述，线路阻抗(Zg)、短路比和电网强度之间的关系如图2所示。此外，在文献[8]中，弱电网由公用电网与线路阻抗模拟器进行串联仿真，通过线路阻抗模拟器调整阻抗来改变SCR。因此，如图1所示，采用反映基于系统阻抗的稳定性特征的等效模型来分析弱电网的稳定性。

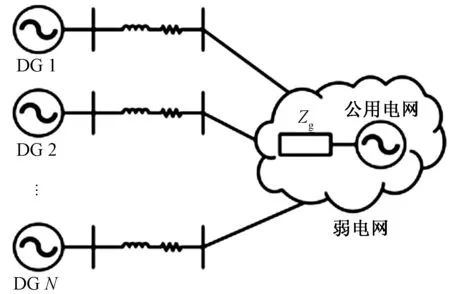
图1 微电网系统结构Fig.1 Microgrid system structure

此外，并网逆变器为弱电网提供恒定功率，通常由P&Q控制器控制。图3所示为带有单个并网逆变器的弱电网的系统配置。其中，如式(1)所示，可以推导出并网逆变器Yinv(s)的具体输入阻抗矩阵。

图2 线路阻抗、短路比和电网强度关系图Fig.2 Relationship between line impedance,short circuit ratio and power grid strength

S为开关；E为电源；C为电容；PCC为功率负载子系统；i为电流；v为电压；θ为初始相位；P为有功功率；Q为无功功率；a、b、c、d、q分别为不同的轴图3 带有单个并网逆变器的弱电网的系统配置Fig.3 System configuration of weak current network with single grid connected inverter

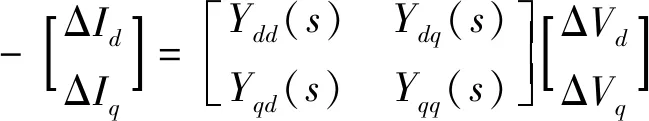
(1)

式(1)中：

(2)

式中：Id0、Iq0、Vd0和Vq0分别为d-q轴上稳定状态运行点的交流电流和电压值；GPPI(s)和GQPI(s)分别为恒定有效功率控制器和直流功率控制器；Gio(s)=GcPI(s)/[sLf+GcPI(s)]，YFF(s)=[1-fFF(s)]/[sLf+GcPI(s)]，GcPI(s)=kcp+kci/s为电流控制回路中PI调节器的传递函数，而fFF(s)=kFF/[TFFs+1]为一阶滤波器。考虑到由多个网格组成的弱电网，上述第i个网格的输入阻抗矩阵可重新定义为Yinvi，其总输入阻抗矩阵为Yinv=Yinv1//Yinv2//…//YinvN。

此外，弱电网的输出阻抗矩阵为

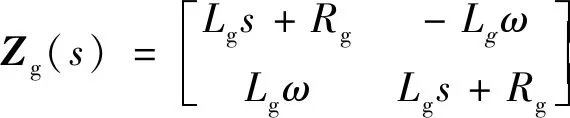
(3)

式(3)中：ω为额定频率。因此，具有N个并网逆变器的弱电网的回比矩阵可以表示为

T0(s)=Zg(s)Yinv(s)

(4)

此外，电网电流i0dq(s)推导公式如下。

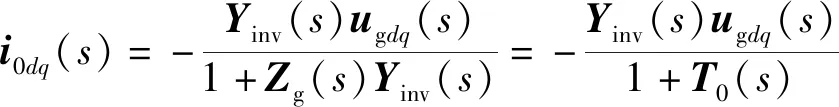
(5)

式(5)中：i0dq(s)=[i0d(s),i0q(s)]T，ugdq(s)=[ugd(s),ugq(s)]T分别为在dq坐标轴中的电网电流和电压。由式(4)可知，如果并网逆变器通过理想电网[Zg(s)=0]连接，则电力系统是稳定的。然而，如果并网逆变器连接在弱电网中，电力系统的稳定性依赖于阻抗回比矩阵T0(s)。因此，只有当1+T0(s)没有合适的极点时，弱网格才是稳定的。换言之，电力系统稳定的充要条件是，回比矩阵的奈奎斯特曲线不包括(-1,j0)点。然而，GNC是复杂的，不适合应用在交流系统的设计。因此，应该提出一个简化的稳定性依据。

2 禁止区域和操作区域的小信号回比矩阵

通过将T0(s)的特征值λTi(i=1,2)稳定在可操作区域内，便可以保证并网逆变器弱电网的稳定性。传统方法中，为了保证系统的稳定性，主要有以下3种禁区标准：Middlebrook准则、增益裕度和相位裕度准则以及反对论点准则。其中，可以在图4中得到上述禁止边界。此外，提出了关于T0(s)的另一个禁止区域，该禁区位于图5的灰色边界的左侧，并且在式(6)、式(7)中给出了建议的禁区。

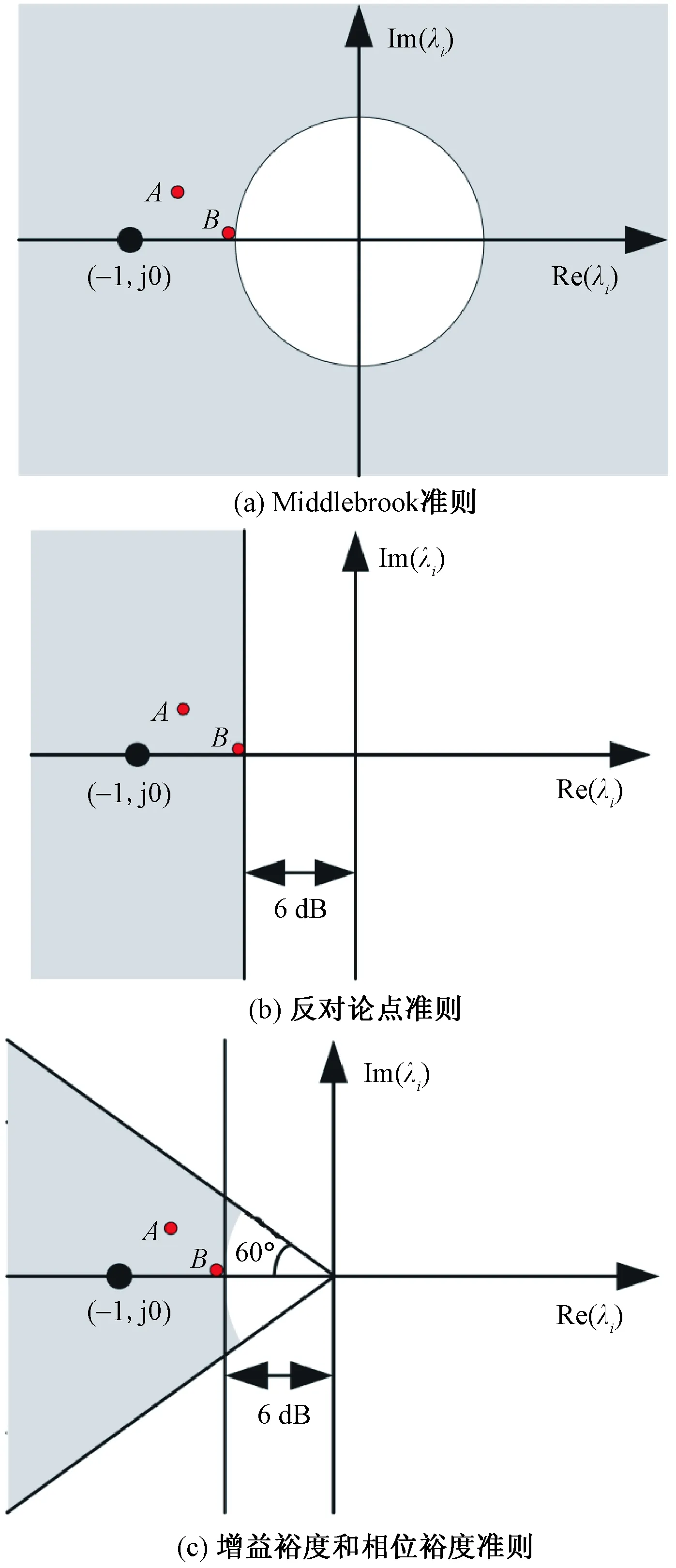
图4 三个公共准则Fig.4 Three common criteria

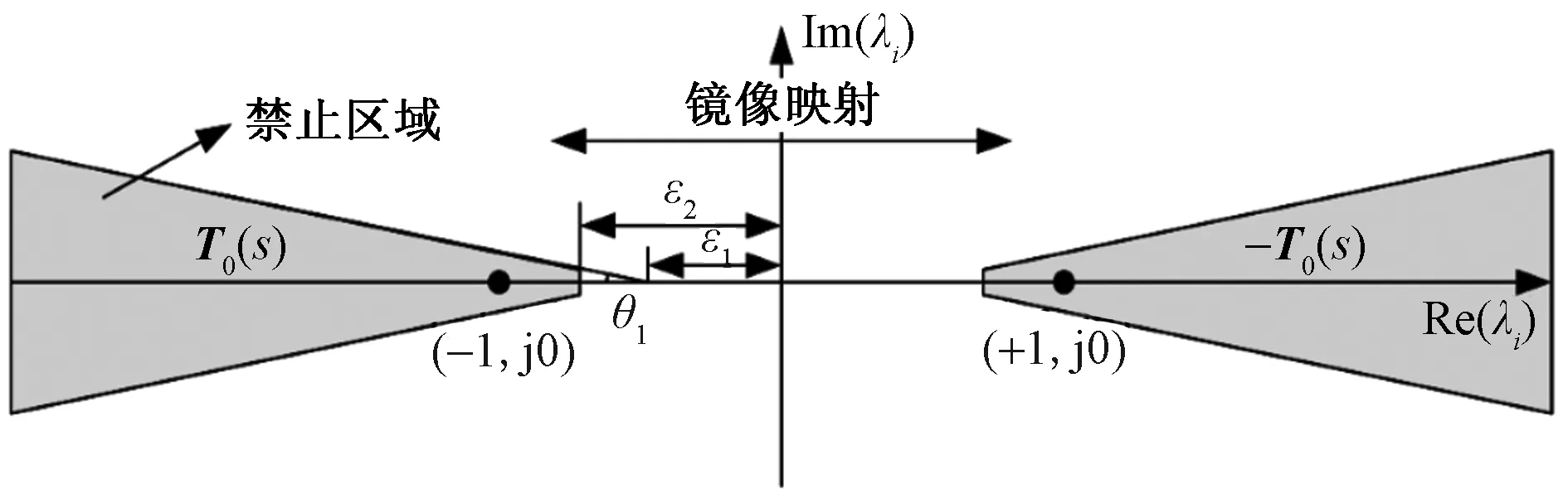
图5 小信号禁区稳定性Fig.5 Stability of small signal forbidden area

|arg(λTi+ε1)|≤180°-θ1

(6)

Re(λTi)≥-ε2

(7)

将λTi设置在该禁区之外，可以保证带有并网逆变器弱电网的小信号的稳定性。同时，将ε1、ε2和θ1设为ε1=0、ε2=0.5、θ1=60°，可以适当将这些参数值增大以降低建议禁区的保守性，如ε1=0.5、ε2=0.95、θ1=5°。从本质上讲，基于范数的阻抗标准是基于Middlebrook禁区判据的，基于范数的阻抗依据的保守性不低于Middlebrook禁止判据。禁区范围越小，准则就越不稳定[11]。结果表明，与现有的3个基于范数的稳定性准则和一般的稳定性禁区准则相比，所提出的禁区准则的保守性更低。此外，如果ε2趋于1，θ1趋于0°，则可以得到稳定性评估的充分必要条件。此外，小信号稳定条件转换为-T0(s)的奈奎斯特围线不包括(-1,j0)点的条件。首先，将T0(s)和-T0(s)分别以Jordan标准形式化简为矩阵，可得

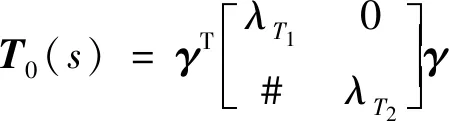
(8)

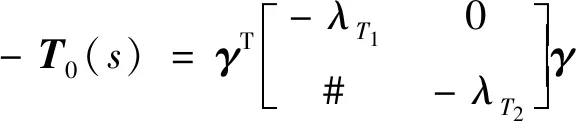
(9)

式中：γ为酉矩阵；#为任意常数。当-T0(s)的奈奎斯特围线不包围(1,j0)点时，满足式(10)，并将其进一步转换为式(10)，即

det[-T0(s)-E]≠0

(10)

=(λT1+1)(λT2+1)

≠0

(11)

式中：E为单位矩阵。并对T0(s)的奈奎斯特曲线不包围(-1,j0)点进行同样的分析，可得

det[T0(s)+E]

=(λT1+1)(λT2+1)

≠0

(12)

因此，如果回比矩阵镜像映射的奈奎斯特曲线不包围(1,j0)点，则保证了电力系统的稳定性。此外，对-T0(s)的禁区进行了重构。它位于图5灰色边界的右侧。此外，小信号稳定运行区域可分为3个分区：R1、R2和R3。它们是通过平移映射和旋转映射获得的，如图6所示。详细的子区域由式(13)～式(15)表示，其中T1、T2和T3是可辨矩阵。将可辨矩阵定义为频率区域上序集的所有特征值都在左半平面上的矩阵。

图6 小信号稳定运行分区Fig.6 Small signal stable operation partition

R1:T1=-T0(s)-ε2E

(13)

R2:T2=-[T0(s)+ε1E]×ej(π/2-θ1)

(14)

R3:T3=-[T0(s)+ε1E]×e-j(π/2-θ1)

(15)

3 电路阻抗协同稳定域

虽然上述等效回比矩阵是传递函数矩阵，但只要确定频率，就可以将其简化为与阻抗相关的线性时不变矩阵[12]。在此基础上，利用基于Guardian Map与Kronecker理论，提出了小信号稳定运行协同区域的计算方法[13]。如果在频率域上的T1、T2和T3有序集的所有特征值都在左半平面上，则弱网格应该是稳定的。因此，将稳定操作协同区域转化为可分辨矩阵的条件可以通过镜像、旋转和平移映射建立的矩阵。

3.1 定义1(Guardian Map)

假设B⊆Rn×n是一个开放集合。如果对于所有T∈B[f(T)≠0]，并且对于所有T∈∂B[f(T)=0])，∂B是集合B的边界，则映射f:Rn×n→R被认为是集合B的Guardian Map[2]，即地图f称为B的Guardian Map。

3.2 定义2(有序集)

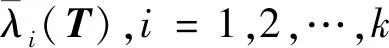
3.2.1 引理1

设T1⊆Rn×n，T2⊆Rm×m，mspec(T1⊕T2)={λi+μj:λi∈mspec(T1)}，μj∈mspec(T2),i=1,2,…,n,j=1,2,…,m，其中⊕表示Kronecker和，mspec(T)表示矩阵T∈Rn×n的多光谱[15]。

3.2.2 引理2

3.2.3 引理3

给定一个向量(ξ1,ξ2,…,ξk)∈Rk,k≥2，存在一个实数r和k-1标量αi∈[0，π),i=1,2，…,k使(ξ1,ξ2,…,ξk)T=rf(α)。其中，α=(α2,α3,…,αk)T∈[0，π)k-1,f(α)=(cosα2,sinα2cosα3,…,sinα2sinα3…sinαk)∈[-1，1]k[17]。

此外，将上述部分建立的等效回比矩阵Ti(i=1，2，3)改写为

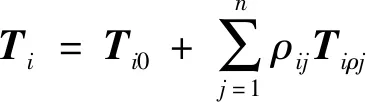
(16)

式(16)中：Ti0为稳定状态点处的等效回比矩阵；Tiρj为线路阻抗变化引起的扰动矩阵；ρij为线路阻抗扰动参数。同时需要讨论两种情况：①由于最小SCR可以近似表示为SCR=1/Lg，因此线路电感的变化可以有效地反映电力系统的强度，因此当n=1时，Tiρ1代表线路电感变化引起的扰动矩阵；②在低、中压电力系统中，线路阻抗不再主要是电感性质的。因此，应提供由电阻和电感组成的阻抗协同稳定工作区，当n=2时，Tiρ1和Tiρ2分别代表电感变化和电阻变化引起的扰动矩阵。

由式(3)可知，电感变化和电阻变化均与回比矩阵呈线性关系。结果表明，在上述两种情况下很容易得到式(15)，其中ρi1和ρi2分别代表电感和电阻扰动参数。此外，可以将通用集合ftab=[f1,f2,…,fj,…,fn]=[1，2，…，20 000]作为频率集合。

3.2.4 定理1

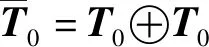
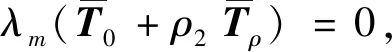
(17)

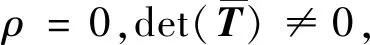
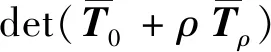
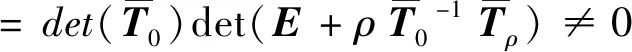
(18)

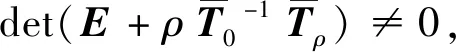
(19)

证明结束。

算法1中描述了解决电路中电感稳定运行区域的步骤。应用相同的计算过程，可以分别基于T2和T3获得电力系统的稳定子区域(R2,R3)。因此，电感稳定区域为R=R1∪R2∪R3。由定理2进一步得到了由电阻和电感组成的阻抗协同稳定工作区域。

算法1 第一种情况的计算过程初始化:R1是满集合,令f=f1;Ti=T1。迭代:j≤n1:根据fj的运行状态,构造T0和Tρ;2:计算T0、Tρ和T0-1Tρ的特征值;3:根据定义2,构造Ψ(T)={r0,r1,…,rk+1};4:确定T是否是ρi∈(ri,ri+1)的可分辨矩阵。如果是,则系统在这个开放集合内是稳定的;5:计算系统稳定时各个开区间的并集,得到线路电感稳定区R1i;6:计算所有稳定区域的交集,即R1=R1∩R1i;7:j=j+1

3.2.5 定理2

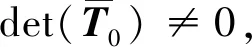
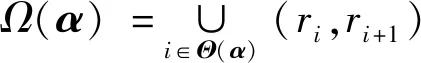
(20)

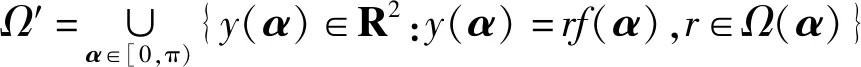
(21)

当且仅当(ρ1,ρ2)T∈Ω′时，T0+ρ1Tρ1+ρ2Tρ2是一个可辨矩阵。

证明：根据引理3，可以将向量(ρ1,ρ2)T∈R2表示为(ρ1,ρ2)T∈r[f1(α),f2(α)]T，其中式(15)中的等价回比矩阵可转换成

T0+ρ1Tρ1+ρ2Tρ2=T0+rTρ(α)

(22)

如果角向量α∈[0，π)是一个单参数矩阵。根据定理1可知，r在α方向上的完全稳定区域可由式(20)得到。由式(21)定义的集合是稳定区域的联合。因此，阻抗协同稳定运行区域为Ω′。

证明结束。

角度集合可以选为通用集合，即αtab=[α0,α1,…,αm,…,180°)=[0°,1°,…,180°)。算法2给出了求解电感和电阻阻抗协同稳定工作区的步骤。与电感稳定区域相似，阻抗协同稳定工作区为R=R1∪R2∪R3。如果电路中电阻和电感的初始值均设置为零，则αtab可以缩小为αtab=[α0,α1,…,αm,…,90°)=[0°,1°,…,90°)。并且，关于算法2中的第8步可以更改为“如果m≤90，则转到步骤1”。

基于本文方法可以通过多次矩阵运算便得到稳定域。而且，随着网格数目的增加，计算复杂度不会增加。

算法2 第二种情况的计算过程初始化:R1是满集合,Rα是空集合,令m=0;f=f1;Ti=T1。迭代:j≤n1:根据定义3的fj以及当前运行状态,构造T0和Tρ(αm);2:计算T0,Tρ(αm)和T0-1Tρ(αm)的特征值;3:根据定义2,构造Ψ(T)={r0,r1,…,rk+1};4:确定T是否是r′i∈(ri,ri+1)的可分辨矩阵。如果是,则系统在这个开放集合内是稳定的;5:计算系统稳定时各个开区间的并集,得到线路阻抗稳定区Rαm;6:计算所有开区间的并集,即Rα=Rα∪Rαm;7:m=m+1;8:如果m<180,返回第一步;9:否则结束;10:计算所有稳定区域的交集,即R1=R1∩Rα;11:j=j+1

4 仿真分析

4.1 基本情况

在本节中介绍了两组并网逆变器仿真，用来证明提出的电路阻抗协同稳定区域识别方法的有效性，包括保守性验证和有效性验证。该方法的测试使用MATLAB2017b编译器，计算机配置为4 GB内存的intel Core i5-4590 CPU@3.30 GHz。其中，模拟测试系统配置与图1相同，具体参数见表1。为降低所提出的禁区准则的保守性，分别令ε1=0.5,ε2=0.95,θ1=5°。

表1 仿真实验测试系统的详细参数Table 1 Detailed parameters of simulation test system

4.2 保守性验证

为了验证提出的小信号稳定禁止区域和稳定域依据的保守性，选取弱电网中的一个网格，参考文献[13]中的结构。其中，弱电网的电阻和电感分别为Rg=1.5 Ω,Lg=0.95 mH。对所提出的禁区准则、三种基于范数的稳定性准则和三种常见的稳定禁区准则进行了仿真比较：首先，由于等效回比矩阵(T0)在0～20 000 Hz范围内不存在正实特征值，因此回比矩阵的两个特征值由于处于禁区之外，此时仿真系统必须是稳定的。其次，在不失一般性的前提下，5 000 Hz以下的回比矩阵为

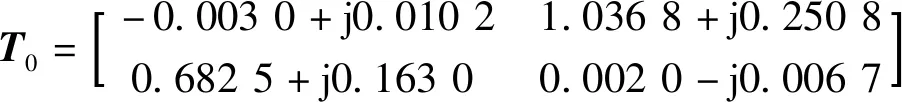
(23)

因此，回比矩阵的两个特征值分别为-0.841 7-j0.200 4和0.840 6+j0.203 9。其中，回比矩阵的负实特征值见图4中的A点。其中，A点位于禁止区域内。因此，根据三种常见的稳定性禁区准则，仿真系统有可能不稳定。另外根据文献[3]，有限范数阻抗准则比其他基于范数的稳定性准则保守性更小。最后给出了有限范数阻抗准则与本文提出的稳定工作区域准则的比较仿真。当频率大于2 744 Hz时，回比矩阵的单位范数的值大于单位值，仿真系统可能不稳定。通过对时域中的电压、电流波形的观察，可以较方便检验相对稳定性判据的性能。如图7所示，电压、电流波形稳定，三相电压和电流的幅值分别为311 V和32.15 A。因此，时域仿真结果与提出的稳定性禁止区域准则的结论是一致的，与现有的基于范数的稳定性准则和三种常用的稳定性禁区准则相比，该准则的保守性更低。

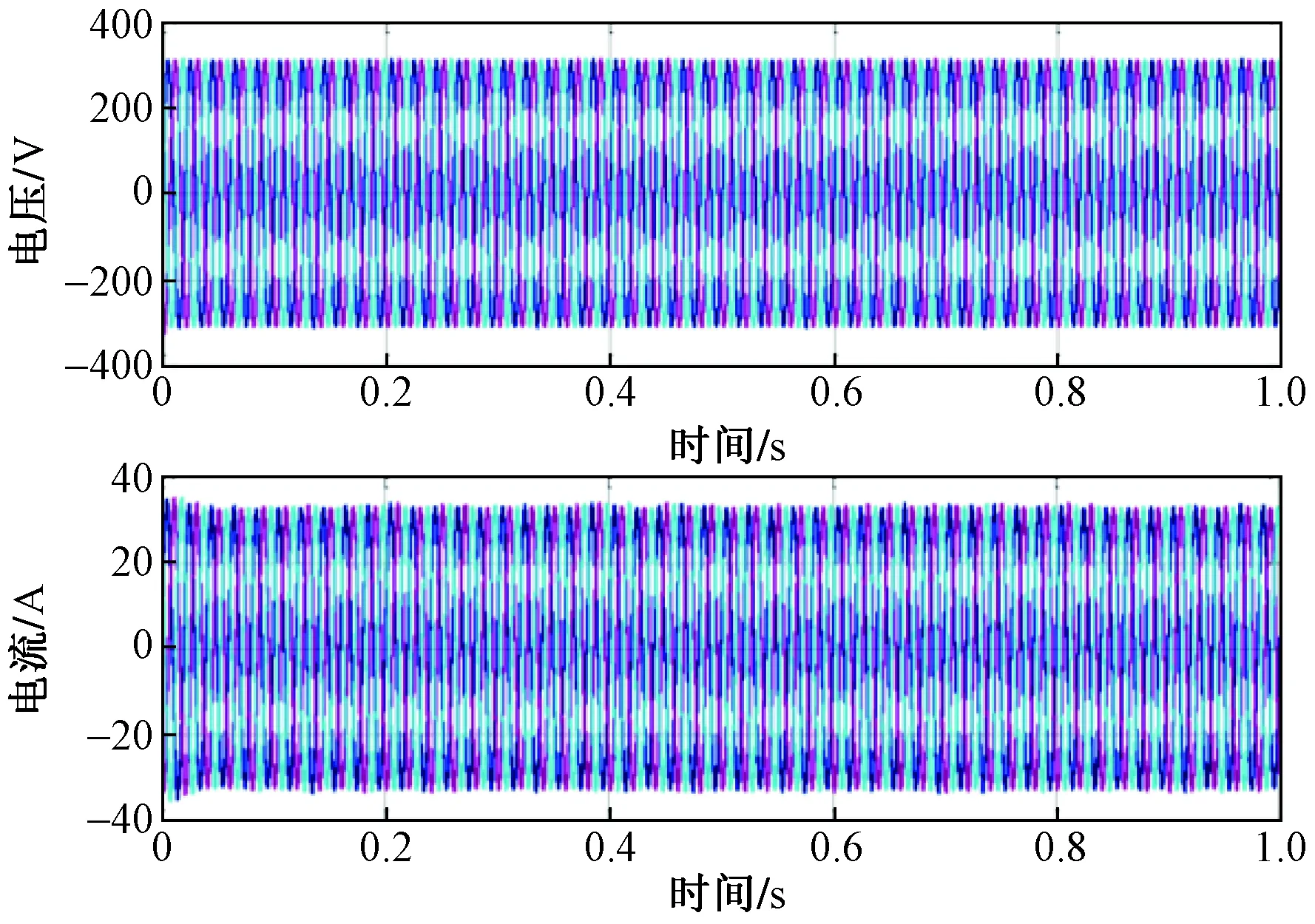
图7 电压、电流波形图Fig.7 Voltage and current waveform

4.3 有效性验证

首先，式(15)可以改写为Ti=Ti0+rsinαTiρ1+rcosαTiρ2，其中rsinα为电路中电感变化区域(Lg=rsinα)，其单位为mH，rcosα为线电阻变化区域(Rg=rcosα)，位于Ω内。此外，算法1可以看作是算法2α=900°时的特例。因此，算法1的验证过程可以嵌入到算法2的验证过程中。此外，线电阻和电感都设置为零，因此αtab被缩小为αtab=[0°,1°,…，90°]，Ti0是一个零矩阵。首先，选择弱电网中的一个网格。根据表1中的相关参数，当线电阻和电感均为零时，等效回比矩阵为差别矩阵。因此，仿真系统必须是稳定的，并且可以通过时域电压、电流波形进行检测。如图8所示，与仿真系统有关的电压、电流波形是稳定的。此外，图9(a)～图9(c)中描绘了3个稳定性分区，分别对应于图6(a)～图6(c)中的子区域。图9(d)中描绘了整个稳定区域，绿色部分为稳定区域。同时，在这种情况下，提出的线阻抗协同稳定区域识别方法的计算时间为4.086 s。根据所提出的稳定运行区域准则，当线阻抗位于图9的绿色区域时，仿真系统必须是稳定的。同时，通过检查时域波形，验证所提出的线阻抗协同稳定域识别方法的结论，仿真系统的稳定性可以很好地得以证明。仿真系统的线路阻抗的参数值为Lg=1.5sin30°=0.75 mH，Rg=1.5cos30°=1.3 Ω。由于线路阻抗位于图9的绿色区域内，仿真系统必须处于稳定状态。如图10所示，在该线阻抗下，电压和电流波形都是稳定的，与本文方法的分析一致。在稳定区边界值(Lg=1.16sin60°=0.00456 mH,Rg=1.16cos60°=10.58 Ω)处仍然进选择线阻抗，如图9所示。同时，时域电压、电流波形是稳定的，如图11所示。由于提出的稳定域准则是一个充分且不必要的条件，因此系统很可能在稳定域边界值处的线阻抗下稳定。最后将仿真系统的线阻抗值改为Lg=10 mH，Rg=15 Ω。显然线阻抗位于图9的绿色区域之外，因此模拟系统可能不稳定，因此时域电压、电流波形也是不稳定的，如图12所示。综上所述，验证了线阻抗协同稳定域识别方法的性能。

图8 理想主电网下单台逆变器仿真系统的时域电压/电流波形Fig.8 Time domain voltage/current waveform of single inverter simulation system in ideal main grid

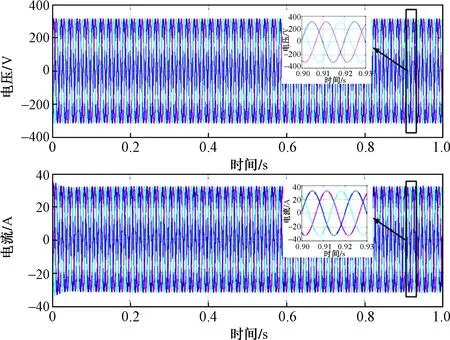
图10 单台逆变器仿真系统在Rg=1.3 Ω和Lg=0.75 mH时的时域电压/电流波形Fig.10 The time-domain voltage/current waveforms of the single inverter simulation system under Rg=1.3 Ω and Lg=0.75 mH

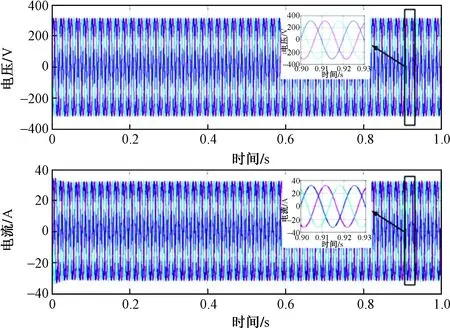
图11 单台逆变器仿真系统在Rg=1.004 56 Ω和Lg=0.75 mH时的时域电压/电流波形Fig.11 Time domain voltage/current waveform of single inverter simulation system at Rg=1.004 56 Ω and Lg=0.75 mH

图12 单台逆变器仿真系统在Rg=15 Ω和Lg=10 mH时的时域电压/电流波形Fig.12 Time domain voltage/current waveform of single inverter simulation system at Rg=1.004 56 Ω and Lg=0.75 mH

为了进一步验证线阻抗协同稳定区域识别方法由多个网格构成的弱电网中的有效性，搭建了由3个网格组成的仿真系统。具体系统参数见表1，为了使实验应用范围更广，将这三个网格的有功功率分别设置为15、15和7.5 kW。3个稳定子区域如图13(a)～图13(c)所示，依次对应于图6(a)、图6(c)中的子区域。整个稳定区域如图13(d)，其中绿色部分为稳定区域。另外，在这种情况下，线阻抗协同稳定域识别方法的运行时间为4.088 s，通过观察稳定区域面积可知，随着网格数目的增加，系统稳定性降低。根据提出的稳定工作区域，当线阻抗位于图14的绿色区域时，仿真系统必须是稳定的。通过对时域波形的检验，验证了该方法的结论，从而证明了仿真系统的稳定性。令仿真系统的线阻抗参数值为Lg=0.35 mH，Rg=3 Ω。由于线阻抗位于图13的绿色区域，因此仿真系统必须稳定。如图14所示，在这种线阻抗下，电压和电流波形都是稳定的，与提出的方法的结论一致。将仿真系统的线阻抗改为Lg=0.5 mH，Rg=5 Ω。显然线阻抗位于图13的绿色区域之外，仿真系统可能不稳定，同时时域电压、电流波形也是不稳定的，如图15所示。从而验证了线阻抗协同稳定区域辨识方法在多逆变器情况下的性能。

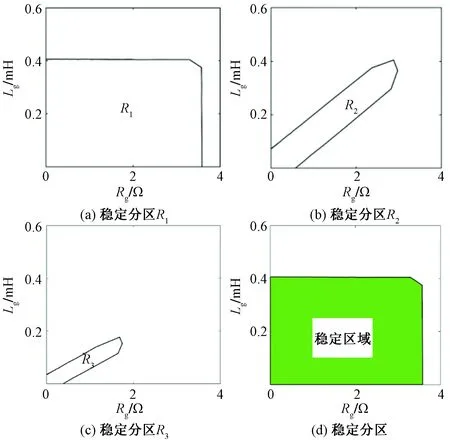
图13 多电平变换器下的线路阻抗协同稳定域Fig.13 The cooperative stability region of line impedance in multilevel converter

图14 多逆变器仿真系统在Rg=3 Ω和Lg=0.35 mH下的时域电压/电流波形Fig.14 Time domain voltage/current waveform of multi inverter simulation system under Rg=3 Ω and Lg=0.35 mH

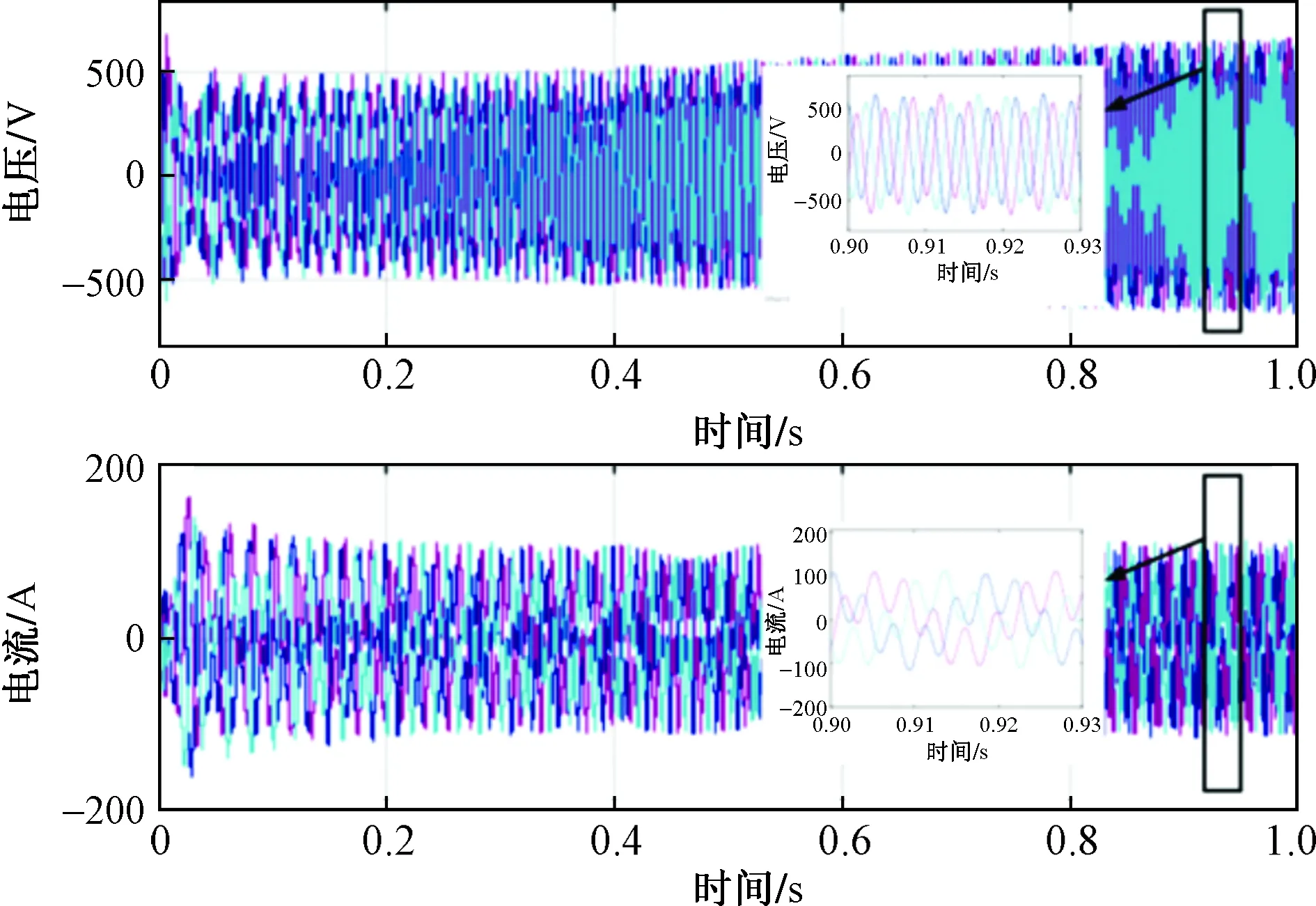
图15 多逆变器仿真系统在Rg=5 Ω和Lg=0.5 mH下的时域电压/电流波形Fig.15 Time domain voltage/current waveform of multi inverter simulation system under Rg=5 Ω and Lg=0.5 mH

5 实验结果

实验平台采用TMS320F28335和Xilinx-Spartan6 FPGA，实验环境设置为550 W、55 V、50 Hz。实验参数如表1所示。与仿真结果相似，初始线电阻和电感均设为零，使αtab变小，Ti0为零矩阵。基于算法2，得到的线阻抗协同稳定区域如图16所示，其中绿色部分为稳定区域。图16(a)～图16(c)依次对应于图6(a)～图6(c)中的子区域。这样设计人员可以方便地获得详细的线电感和电阻的协同稳定域。根据本文提出的稳定运行区域，当线路电阻和电感都位于图16的绿色区域时，实验系统将是稳定的。同时，通过对时域波形的检测，验证了本文提出的线阻抗协同稳定区域辨识方法的结论，以及实验系统的稳定性。将实验系统的线电阻和电感值设为Lg=5 mH，Rg=5 Ω，位于图16的绿色区域，此时实验系统处于稳定状态。但是35 Hz下回比矩阵的负实特征值在禁止区域，如图4中的B点所示。此外，当频率从72 Hz升高到482 Hz时，回比矩阵的单位范数值大于单位值。根据有限范数稳定性准则和三种常见的稳定性禁区准则，实验系统可能是不稳定的。此外，在该线阻抗下，电压波形是稳定的，与提出的协同稳定区域的结论一致。此外，将实验系统的线电阻和电感值改为Lg=10，Rg=12 Ω。显然线电阻和电感都位于图16的绿色区域之外，因此实验系统可能不稳定，同时，时域电压波形也是不稳定的。因此，上述实验结果可以充分验证线阻抗协同稳定区域辨识方法的性能。