吸附作用下煤体变形叠加关系研究

贾立锋，董 擎，梁 冰，孙维吉

（1.安阳工学院，河南 安阳 455000；2.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000）

在瓦斯流动过程中，围岩应力、瓦斯压力、吸附/解吸作用均会引起煤体变形[1]。围岩应力和瓦斯压力变化时，煤体受到的有效应力变化引起的煤体变形为有效应力变形；吸附/解吸作用下引起基质表面能变化产生的膨胀/收缩变形为纯吸附/解吸变形。当围岩应力恒定时，孔隙压力变化既引起了有效应力变形，又产生纯吸附/解吸变形。目前，煤体变形由吸附膨胀（解吸收缩）应力和有效应力共同作用已经成为共识，当不考虑煤体内层理、端割理、面割理的影响时（各向同性），部分学者认为纯吸附/解吸变形和有效应力变形可以进行叠加。1996年，何学秋[2]最先建立了煤体变形与瓦斯压力作用变形、纯吸附膨胀变形之间的函数关系，认为煤体变形可由纯吸附膨胀变形减去瓦斯压力压缩变形；2005年，吴世跃[3]首次考虑了有效应力与膨胀应力的关系，建立考虑有效应力作用煤体变形公式；郭平等[4-5]基于煤-气吸附界面的表面自由能变化等于煤体弹性能变化的基本假设，从理论上推导了吸附膨胀变形表达式和吸附膨胀应力表达式；祝捷等[6-7]建立考虑吸附/解吸变形随时间变化的煤体变形力学模型；此外，梁冰等[8-9]开展了横观各向同性煤等温吸附变形实验，从压力作用和吸附膨胀变形机理的角度间接检验了吸附平衡压力和煤吸附变形的关系。但是由于纯吸附变形是表面能变化引起的变形，实验测试纯吸附变形时会受到瓦斯压力变化引起压缩变形的影响，为了排除瓦斯压力的干扰，对该叠加关系检验需要更为合理的验证方法。因此，在吸附膨胀变形机理的基础上，提出了吸附作用下煤体变形叠加关系验证方法，利用该方法结合已经公开的实验数据对吸附作用下煤体变形叠加关系进行检验。煤体变形叠加关系的研究，对建立考虑煤体结构特征的吸附/解吸本构方程，进一步丰富气固耦合理论，煤层瓦斯抽采效果评估、煤层瓦斯抽采参数优化有重要意义。

1 煤体变形叠加关系验证方法

基于吸附膨胀理论提出一种煤体变形叠加关系验证方法，该方法基于以下4点假设：①煤体吸附过程的环境等温；②煤体的变形为宏观变形，相同应力下吸附平衡前后煤体的弹性模量等参数不发生变化；③氦气吸附不会引起煤体产生变形；④等温吸附曲线符合朗格缪尔方程。

煤吸附膨胀变形普遍认为是煤基质吸附膨胀应力（解吸收缩）和有效应力共同作用的结果。将吸附过程简化为2个过程：首先是吸附压力p作用下的绝对吸附变形，其变形量为εa；其次是在有效应力σet作用下的压缩变形，其变形量为εc。煤体吸附变形为吸附膨胀应力和有效应力作用下变形，其变形量为ε。煤体吸附变形示意图如图1。

图1 煤体吸附变形示意图Fig.1 Schematic diagram of coal body adsorption deformation

如果吸附作用下煤体变形满足叠加关系，那么：

若要证明式（1）成立，只需验证式（2）成立即可。

前人研究表明绝对吸附膨胀变形量εa可以用式（3）描述[2]：

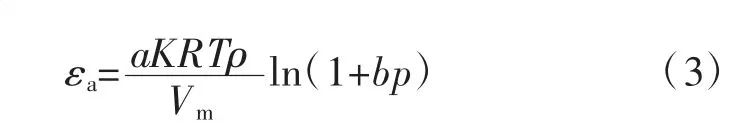
式中：a为吸附剂的极限吸附量，m3/t；K为比例常数；R为普适气体常数，取8.3145J/（mol·K）；T为吸附温度，K；ρ为吸附剂密度，kg/m3；b为吸附常数，MPa-1；p为吸附平衡压力，MPa；Vm为气体的摩尔体积，取22.4×10-3m3/mol。

同一块煤样，式（3）中的参数均相等。利用2个不同的压力测点和下的绝对吸附膨胀变形量比值消除难以求解的参数，并结合式（2），得：

式中：εi、εj为煤体总线应变，通过煤体吸附甲烷实验确定；εci、εcj为煤体压缩线应变，通过煤体吸附氦气实验确定。

对于式（4）的验证，需要对公式中的参数进行求解。公式等号左边项通过理论计算获取，公式等号右边项中参数通过实验获取。最后对公式等号左右两边求得数值进行误差分析，验证吸附作用煤体变形叠加关系的合理性。

2 吸附作用煤体变形叠加关系的验证

目前已经有学者对吸附/解吸煤体变形开展了大量的实验研究，为了保证吸附/解吸煤体变形叠加关系验证的严谨性，验证数据来自于文献[10]。文献[10]开展了氦气和甲烷作用下煤体吸附应变动力学特征研究，实验温度为30℃，甲烷吸附曲线符合朗格缪尔方程。实验使用了6块型煤试样，其中编号Y8R、Y8、Y7为无烟煤，H4为瘦煤，W8、W7为1/3焦煤，吸附常数b分别为1.204（Y8R）、1.234（Y8）、1.300（Y7）、0.821（H4）、0.453（W8）、0.325（W7）MPa-1。根据文献[10]中煤样吸附氦气和甲烷的拟合公式（拟合公式相关性系数均大于0.99），反演出吸附平衡压力为1、2、3、4、5、6、7MPa时的体积应变，煤吸附/解吸体积应变计算结果见表1。

由于式（4）为单一方向上的线应变，而表1中测得的体应变。线应变和体应变之间的关系如下：

表1 煤吸附/解吸体积应变计算结果Table1 Calculation results of coal adsorption/desorption of volumetric strain

式中：εv为体应变；ε1、ε2、ε3为3个主应力方向的线应变。

由于型煤具有各向同性的性质，吸附时试样各个方向的线应变情况相等。

将式（5）和式（6）代入式（4）可得：

式中：ε1i、ε1j为压力pi和pj下的主应力方向总线应变；ε1ci、ε1cj为压力pi和pj下的主应力方向压缩应变；εvi、εvj为压力pi和pj下的总体应变；εvci、εvcj为压力pi和pj下的压缩体应变。

式中：Kij为不同实验条件下理论值比例系数；Hij为不同实验条件下实验值比例系数。

因i和j的取值为1～7MPa的整数，且i与j不等。所以，Kij和Hij分别有42个数据，将表1中的数据代入式（8）和式（9），求出Kij和Hij。不同试样理论值比例系数和实验值比例系数关系如图2。

图2 不同试样理论值比例系数和实验值比例系数关系Fig.2 Relationship between proportions of theoretical values and experimental values of different samples

从图2可以看出，无烟煤（Y8R、Y8、Y7）、瘦煤（H4）、1/3焦煤中W8理论值比例系数和实验值比例系数均在y=x函数附近，符合式（7）；焦煤试样W7对于理论值比例系数和实验值比例系数小于2.5 的值符合式（7），大于2.5 的值略有偏差。每个试样得到的数据点较多，采用统计方法分析误差更为合理，因此引入平均相对误差公式：

式中：δMAE为平均相对误差。

不同试件的平均相对误差见表2。

表2 不同试件的平均相对误差Table2 Average relative error of different samples

从表2可以看出，除了W7的误差为9.53 %外，其余误差均小于4.24 %。无烟煤、瘦煤、1/3焦煤6块试样平均相对误差的均值为4.27 %，实验数据验证结果表明式（1）成立，吸附作用下煤体变形是纯吸附膨胀变形和有效应力变形的叠加。

3 解吸作用下煤体变形叠加关系讨论

在理想情况下吸附和解吸互为可逆过程，随瓦斯压力变化的吸附变形曲线与解吸变形曲线重合。前人实验结果表明：煤吸附膨胀变形和解吸收缩变形存在3种情况：①可逆变形：即吸附变形曲线与解吸变形曲线重合[11-12]；②残余变形：即解吸曲线应变值高于相同瓦斯压力下吸附应变值[13-14]；③富裕变形：即解吸曲线应变值低于相同瓦斯压力下的吸附应变值[15]。瓦斯压力变化过程中煤体解吸变形示意图如图3。

图3 瓦斯压力变化过程中煤体解吸变形示意图Fig.3 Diagram of coal desorption deformation during gas pressure change

目前普遍认为瓦斯压力降低后，吸附气体残留在煤胶粒结构内部，部分游离气体被禁锢在微孔隙和微裂隙中，因此当气体解吸后，煤体存在一定的残余变形。而富裕变形本质上受游离态瓦斯引起的膨胀变形能力、游离态瓦斯析出引起孔隙和裂隙闭合导致的收缩变形能力以及塑性变形能力综合影响。

利用文献[10]数据验证了吸附作用下煤体变形的叠加关系，但由于解吸过程存在可逆变形、残余变形、富裕变形3种情况，提出的煤体变形叠加关系验证方法应用于解吸变形曲线时存在一定的局限性。当解吸曲线是可逆变形时，与吸附作用下煤体变形叠加关系的验证方法得到的误差相同。当解吸曲线有残余变形存在，解吸作用下不同平衡压力下的理论值比例系数和实验值比例系数的平均相对误差必然与吸附作用下不同；当解吸曲线为富裕曲线时，在低压的情况下实验值比例系数可能存在负值，而理论值比例系数恒大于0，因此这种情况下无法验证。

4 结 语

1）基于吸附膨胀理论提出1种验证煤体变形是由吸附膨胀变形和有效应力变形叠加而得的方法。

2）经验证吸附作用下煤体的变形可以由纯吸附膨胀变形和有效应力变形叠加而得。

3）煤体变形叠加关系验证方法适用于可逆变形、残余变形的解吸曲线，不适用于富裕变形的解吸曲线。