基于平面应变下扩展SMP 准则的土体强度公式

张宁宁

（1.河北省水利规划设计研究院有限公司，石家庄 050021；2.西北农林科技大学水利与建筑工程学院，陕西咸阳 712100）

平面应变状态是目前工程中广泛存在的一种应力状态，这种应力状态只在平面内有应变，而与该平面垂直方向上应变可以忽略，但存在一定的压应力。具有这种特性的物体其一个方向的尺寸（通常沿轴线方向）比另外两个方向的尺寸大很多，且沿轴线方向的横截面形状和大小无变化，如重力坝、堤防及条形基础等。 分析土体处于平面应变状态下的强度与变形是工程中经常遇到的一个问题， 但在平常工作中却忽略了这种特殊应力状态， 常以常规三轴压缩试验得到的强度指标（c、φ）来代替平面应变状态下的强度指标，这种代替显然不符合实际情况；三轴试验的三向应变均不为零， 而当土体处于平面应变状态时，其中主应力σ2方向（通常沿轴线方向）的应变dε2=0， 这就对土体在dε2方向的变形发展得到了限制，进而使得中主应力σ2变的更大，这种应力状态不仅对土体的强度有一定增强作用， 而且还随着土体的有效内摩擦角的增大而增大， 即采用常规三轴试验的强度指标用于平面应变状态下是偏于保守的，这种强度指标只能作为参考使用，并不能代替，但两者又有一定联系。因此，建立两种应力状态下的强度参数之间的关系式有重要意义。

诸多研究者对于平面应变状态下土体的内摩擦角φps值和三轴压缩状态下土体的内摩擦角φtc值两者之间提出了各种关系式。 朱思哲［1］通过试验证明在平面应变状态下， 土体的强度和变形特性与三轴试验的结果有明显不同，对于同样的砂，平面应变下的φps值约比三轴压缩下的φtc值高出4°～7°，并且提议在选取土体强度参数φ时，取平面应变的φps值比三轴压缩下的φtc值要经济合理。 姚仰平等［2-3］将本构模型与SMP准则相结合考虑了应变增量方向与应力方向的非共轴性，并给出了扩展SMP准则。

本文基于扩展的SMP准则和佐武的平面应变状态， 推导建立了适合各种应力状态下的一般黏性土体的平面应变强度公式， 并且通过试验验证了该公式的合理性。

1 一般黏性土的破坏准则

1.1 渍ps与渍tc之间关系推导

对于各项同性的无黏性土， 三轴压缩状态下对应明确的应力条件（滓1＞滓2=滓3）和应变条件（dε1＞dε2=dε3）； 而土体在平面应变状态下只对应着明确的应变条件（dε2=0），应力条件不确定。 因此，通过理论建立平面应变状态下的应力条件， 对于研究其强度公式是非常必要的。 Satake［4］推导出了平面应变状态下的应力条件：

图1显示， 在子～滓空间上两个应力摩尔圆的公切线恰好通过坐标原点， 这表明由应力比控制的摩擦性材料， 在平面应变状态下两个小摩尔圆具有相等的贡献。

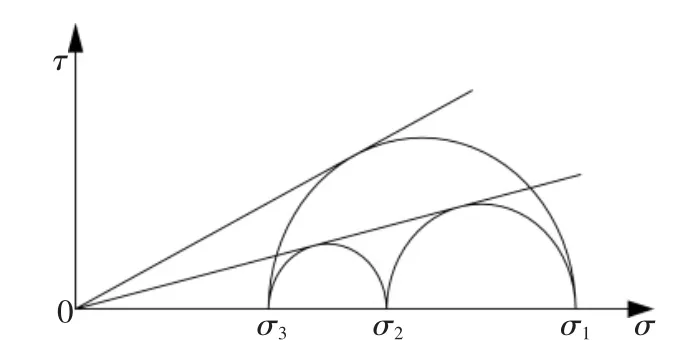
图1 摩擦性材料的Mohr圆

式（2）中建立滓1、滓2及滓3之间的关系，可以绘制图2所示的摩尔圆， 两个小摩尔圆的公切线为水平直线，这表明对于由剪应力控制的金属（黏着性）材料，在平面应变状态下两个小摩尔圆具有相等的贡献。

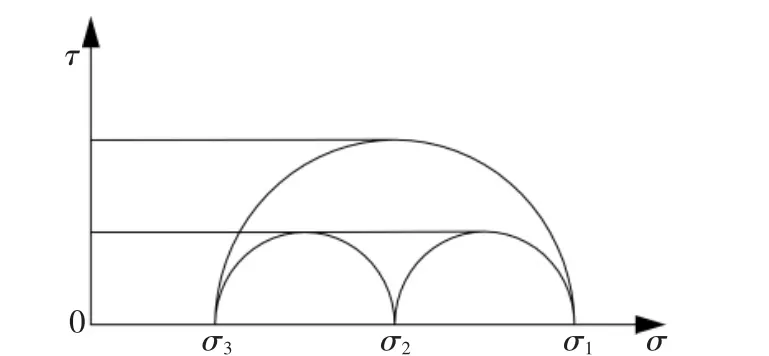
图2 金属材料的Mohr圆

由式（1）与（2）知，材料的特性不同，平面应变状态下中主应力与其他两个主应力滓1、滓3的关系也不同。

对于完全摩擦性的无黏土， 由上文可知应力摩尔圆的公切线均会通过坐标原点， 但在实际中土体并非完全摩擦性材料， 强度破坏包线一般不通过原点，与子轴有一定截距。 假设强度破坏包线总是通过一个公共点O0，如图3。

图3 扩展的SMP准则

式（13）就是根据扩展的SMP破坏准则和Satake的平面应变状态下的应力条件式得出的平面应变下一般黏性土体的破坏条件。 若把平面应变状态下土体的内摩擦角用φps表示，则按照内摩擦角的定义：

式（15）为平面应变状态下内摩擦角φps与三轴压缩条件下内摩擦角φtc之间的函数关系， 绘制φps与φtc之间的关系曲线如图4。

图4 φPS与φtc之间的关系曲线

由图4可看出， 当内摩擦角在0°＜φtc＜90°范围内时，φps＞φtc。 所以平面应变状态下的内摩擦角大于三轴压缩条件下的内摩擦角， 但目前的实际工程平面应变的分析中采用三轴压缩试验得到的抗剪强度参数φ是偏于保守的。 由图还可看出，φps与φtc有良好的相关关系，φps可用φtc来表示，其关系式为：

且相关系数高达R2=0.9998。

1.2 cps与ctc之间关系推导

在平面应变下一般材料的Mohr-Coulomb破坏准则为：

图5 kps与φtc之间的关系曲线

2 试验值与预测值比较

本文采用泾阳、杨凌、子洲、北杨村及兰州5个不同地区的黄土分别进行平面应变试验及三轴压缩试验，来验证公式的合理性［7］。 图6为φps的试验值与预测值结果比较； 图7为cps的试验值与预测值结果比较。 由图6知，不同地区的黄土在平面应变状态下的内摩擦角φps预测值与实测值相接近，说明式（15）理论推导的正确性及合理性。 由图7可知，不同地区的黄土在平面应变状态下的黏聚力cps实测值均落到预测值区域范围内，说明式（2）～式（23）理论推导的正确性及合理性。

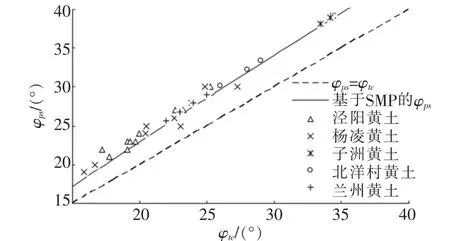
图6 φps的试验值与预测值结果比较

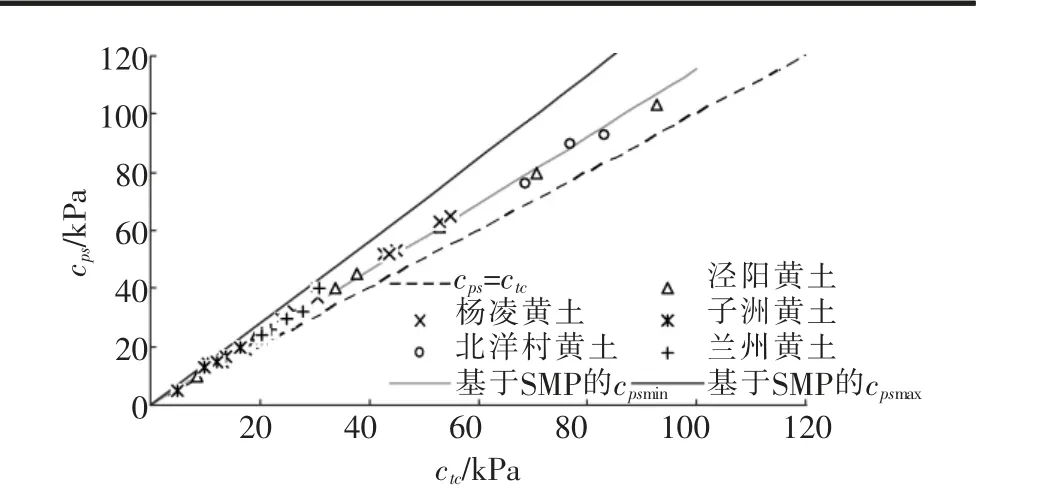
图7 cps的试验值与预测值结果比较

3 结语