改进自适应MOEA/D算法的楼宇负荷优化调度

2022-01-25易灵芝林佳豪刘建康罗显光

计算机工程与应用 2022年2期

易灵芝，林佳豪，刘建康，罗显光，李旺

1.湘潭大学自动化与电子信息学院&湖南省多能源协同控制技术工程研究中心，湖南湘潭 411105

2.湖南省风电装备与能源变换2011协同创新中心，湖南湘潭 411101

3.大功率交流传动电力机车系统集成国家重点实验室，湖南株洲 412001

随着化石能源的不断开采和使用，促使风能、太阳能等可再生能源的发展和利用已成为当今社会的重要任务[1]。能源消耗与当今社会之间的关系日益紧张，加上全球变暖、污染排放等环境问题，促使了加快可再生清洁能源的消纳[2]。需求响应[3]通过价格的变动或激励促使用户调整自身用电习惯减少用电，是智能电网的核心部分[4]。需求响应，通过分析用电负荷特征和用户用电需求，利用家庭智能开关控制智能家居设备的通/断状态，并结合可再生清洁能源和储能电池联合达到降低用电负荷峰谷差和降低用户电费的作用，保证用户侧的用电经济性和稳定性[5]。由于电力市场与用户需求之间的不断变化，导致阶梯电价和分时电价下用户参与价格需求响应的积极性降低以至影响削峰填谷的效果。实时电价有效地解决了分时电价下峰谷平时段交界处采用相同电价的不合理问题，同时也避免多数用户向低电价时段用电的回弹现象[6]。因此，基于实时电价下的智能楼宇负荷日调度研究具有重要意义。

近年来许多学者对用户侧负荷调度展开了一些研究，Althaher等人[7]提出家用电器能源管理控制器求解混合整数非线性优化问题，通过当天电价的波动来控制能源控制器的开断，在满足一定用户用电舒适度的条件下实现用户用电费用降低，并设置功率阈值避免用户集体向低电价时段用电造成新的用电峰期，在实现用户电费和保持用户用电舒适度上有不错的效果，但是没有考虑新能源消纳和用电峰谷差。文献[8]中针对用户用电费用和住户用电舒适性，利用核密度估计方法提取带有定时器装置负荷的概率模型，运用数据驱动策略优化求解负荷调度模型，由于没有从整个用户所有可调用电负荷进行优化，在降低电费上可以体现得更加充分。Joo等人[9]建立了二级家庭分布式能源管理系统，并针对空调、洗衣机等负荷设置用户使用偏好和用户用电舒适度建立数学模型，提出分布式优化算法对目标寻优，仿真算例验证了电费和用户舒适度的有效性。文献[10]构建了居民用电管理系统优化模型，针对空调、洗衣机、电动汽车等负荷进行优化调度，以用电电费最小为目标函数，但是未考虑新能源消纳和储能负荷。上述文献对家庭用户负荷进行优化调度，针对负荷侧能源优化管理存在多种数学模型，如何寻找并有效运用优化算法对其求解得出满意调度方案和可再生能源利用率都是目前存在的难题。由于目前负荷侧优化调度做法未考虑新能源的接入，而新能源的加入能有效缓解当前能源短缺的现状，因此本文引入可再生能源，提高能源利用率。

本文针对上述问题，提出一种智能楼宇住户负荷优化调度策略。该策略通过对负荷特性的分析和用电住户的用电信息描述将用户和负荷进行分类并建立相应的ADR数学模型。以用电费用最小、新能源消纳最大和用电峰谷差最小为目标建立数学模型，通过改进自适应权重向量和自适应选择策略的MOEA/D算法对优化调度模型进行寻优求解，实现了用户侧电费降低、促进了新能源的消纳并保证了负荷侧楼宇住户的稳定性。

1 问题描述

自动需求响应（automatic demand response，ADR）是用户与电网之间的桥梁，通过电网电价或激励政策来促使住户对响应做出相应改变，通过自动调整用电策略实现经济性。ADR降低了用户侧费用并减少电网用电峰谷差达到电网削峰填谷的作用，既提高了新能源消纳和用户对电力市场的经济性，又加强了电网的稳定性[11]。

将楼宇居民用电负荷分为两大类。第一类为不参与调度的不可控负荷，第二类为可控负荷，包括可中断负荷、可转移负荷、充电负荷和储能负荷。下面搭建各类负荷模型，并分析其约束条件。

1.1 可中断负荷

由于存在热惯性，空调类可中断负荷在短时间内停电不影响签约住户居民舒适性，可调度空间较大，基于时间参数的模型为：

其中，Ti,min,on为负荷i最小需要允许运行时间，Ti,max,off为其最大允许可中断时间，Ti,t,on、Ti,t,off分别为其连续运行时长和连续关断时长，Tstart、Tend分别为可调度的起始时间和结束时间。

1.2 可转移负荷

洗衣机等可转移负荷持续运行时间固定，可以将负荷运行时间在可调度范围内平移，基于时间参数的模型如下：

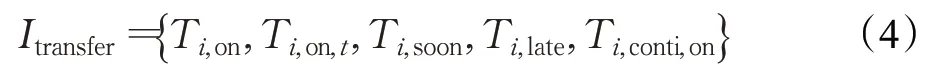
其中，Ti,on、Ti,on,t分别为负荷i的开始运行时间和持续运行时间，Ti,soon、Ti,late分别为负荷i最早和最晚可调度时间，Ti,conti,on为负荷i需持续运行时间。

1.3 充电负荷

设定签约住户拥有充电汽车，基于时间参数的充电负荷模型如下：

其中，Ti,on、Ti,off分别为充电汽车i充电开始时间和结束时间，Ti,start、Ti,end分别为其可调度充电开始时段和结束时段，为充分利用夜间峰谷电力，建议选取22点和次日7点。

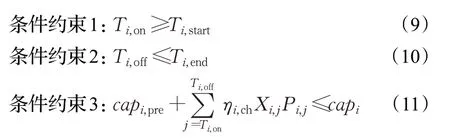
其中，capi为负荷最大充电容量，capi,pre为负荷i初始储能电量，ηi,ch为负荷i的充电效率，Xi,j为负荷i在第j时段的负荷状态（0：不充电，1：充电），Pi,j为i负荷在j时段的运行功率。

1.4 储能负荷

基于时间参数的蓄电池组储能模型为：

其中，Tin,on、Tin,off分别为蓄电池开始充电时间和结束时间，Tout,on、Tout,off分别为蓄电池放电开始时间和结束时间。

储能电池在m用电时段的剩余存储电量为：

其中，capi,pre为每日零点的初始剩余电量，ηch为充电效率，ηdi为放电效率，Xi,j为设备i在j时段的运行状态（11：放电；10：充电，00或01：挂起）。Pi,j为设备i在j时段的充放电功率，capi,h为设备i在h时段的容量，αi,max、αi,min分别为最大和最小充放电程度百分比。

储能负荷受最大和最小充放电使用程度约束，约束条件为：

1.5 新能源发电设备

作为电能输入，新能源发电设备以光伏发电为主，暂考虑其发电量与发电时间，且电价与电网电价一致。光伏电能直接供给楼宇住户使用，将多余的电能储存在蓄电池备电。基于时间参数的发电设备为：

其中，Tnew,start、Tnew,end分别为新能源发电开始时间和结束时间，Tinstart、Tinend分别为蓄电池充电开始时间和结束时间，Toutstart、Toutend分别为蓄电池放电开始时间和结束时间。

1.6 优化目标

以住户用电电费、新能源消纳率，用电峰谷差为目标函数进行数学建模。目标函数如下：

N为一户中共设备总数，H为总用电时段，Ti,j为设备i第j用电时段，cj为j时段的实时电价数据，Pi,j为设备i在j时段的运行功率。

新能源消纳率U与丢弃率Y关系为：

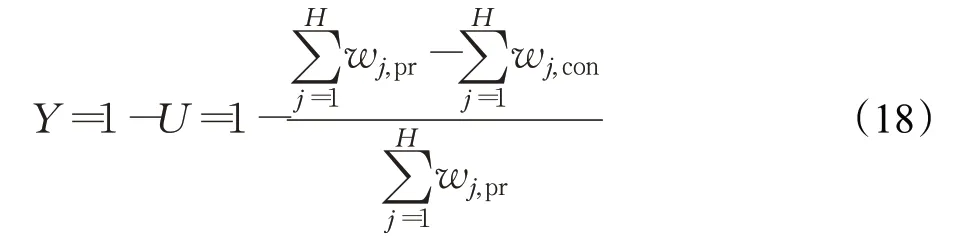
H为总用电时段，wj,pr为新能源在第j时段产生的电量，wj,con为新能源第j时段利用消纳的电量。

日用电峰谷差为：

前一项为N个负荷一天中第j时段最小功率总和，后一项为N个负荷一天中第j时段最大功率总和。

1.7 ADR负荷控制编码

决策变量为签约住户中每种负荷通/断状态顺序编码，各类可控负荷统一由智能开关来控制通断状态，因此将1天24小时以15分钟为单位分为96个时间段，每个时间段每个设备的开断状态用0-1状态编码，其中储能设备的可控编码为00、01或11编码表示，通过此负荷控制编码可以算出式（17）、（18）、（19）的适应度值并作为算法种群点参与迭代进化，具体编码如图1所示。其中，xin为可中断负荷H维编码，xtr为可转移负荷H维编码，xst为储能负荷2H维编码，控制编码按可中断负荷、可转移负荷、发电新能源、充电负荷和储能负荷的顺序进行编码，图1中只表示了部分编码以做解释。

图1 控制编码Fig.1 Control coding

2 改进自适应权重向量与自适应选择策略的MOEA/D算法

基于分解的多目标进化算法（multiobjective evolutionary algorithm based on decomposition，MOEA/D）是一种利用分解策略解决多目标问题的算法[12]。该算法通过聚合函数将多目标问题分解为N个子问题，每个子问题分配一个对应的权重和相关种群点的邻域[13]。种群迭代通过邻域内随机选择两个父代点交叉产生新的子代点后更新参考点Z，然后通过聚合方法比较子代点与父代点，更新邻域内所有被支配的点，有效地利用局部信息，避免陷入局部最优，最后将非支配解存入外部存档（external population，EP）。MOEA/D通过分解的思想，每一个点（子问题）对应一个权重进行求解，由于权重是均匀分布在目标空间的，故MOEA/D算法相对于其他算法在计算效率提高的同时保证了点的均匀分布[14]。

MOEA/D算法在处理连续多目标问题时具有较好的性能，但点对应的权重较离散时，可能会陷入局部最优。为了缓解这一现象，引入广义分解的思想结合均匀分配权重设计了一种自适应权重向量，算法每次循环后更新权重，使权重更适合于当前的目标空间内点的分布；由于没有适合所有多目标问题的交叉算子，故设计一种基于历史经验自适应选择交叉算子策略，对模拟单点二进制交叉算子（simulated binary crossover，SBX）和差分进化算子（differential evolution，DE）在所有种群中随机分配，对存入外部存档中的非支配解使用的交叉算子进行计数，采用轮盘赌的方式实现自适应选择策略，提升了算法的鲁棒性；为了避免算法陷入局部最优，引入映射思想将产生新的子代种群点进行修正，间接地增加了算法搜索范围，提高了算法种群多样性；采用基于欧式距离计算外部存档中非支配解的稀疏度来更新外部种群。

采用切比雪夫聚合函数，将楼宇微电网负荷调度的住户电费最小、新能源消纳率最高（丢弃率最小），日用电峰谷差最小的多目标问题分解为N个子问题，第j个子问题目标函数如式（20）所示：

2.1 自适应权重向量产生策略

按照广义分解的思想[15]，切比雪夫聚合函数第j个子问题的目标函数可以另表示为式（21）：

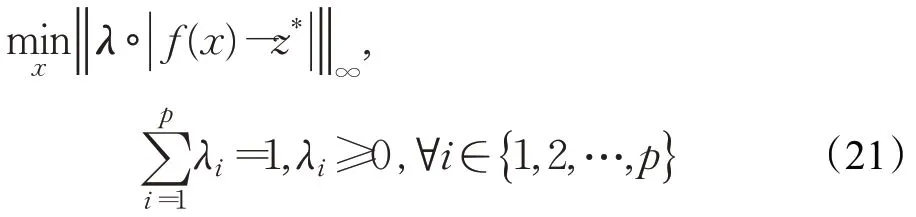
其中，∘表示为权重向量λ与的阿达玛积，代表求无穷范数，p表示维度。从式（21）可以得出生成的非支配解x*，对应唯一确定的权重向量λ*，对应的λ*具有如下性质：

因此通过每一代循环产生的非支配点可以确定相应的非支配权重向量λ*。

自适应权重向量产生具体操作如下：首先运用均匀分配生成一组均匀分布的权重向量λ1,λ2,…,λN[15]。由于切比雪夫聚合函数中权重向量与搜索方向互为倒数[16]，所以将均匀生成的权重向量λN表示为式（23）：

λi的约束条件如式（24）所示：

利用权重向量V=(V1,V2,…,VN)进化迭代产生的每一代非支配解利用公式（21）计算出唯一确定的相对较优权重向量ε1,ε2,…,εN，将得出来的新权重向量ε1,ε2,…,εN与V=(V1,V2,…,VN)相加得到需要的自适应权重向量δ1,δ2,…,δN。

2.2 基于历史经验的自适应交叉算子选择策略

种群交叉进化是算法中核心部分，它直接影响了算法搜索策略的多样性和帕累托前沿的准确度。如没有免费的午餐定理[17]解释，通常单一的交叉算子难以兼顾每一个多目标问题的多样性和算法的鲁棒性，故将多种交叉算子结合使用使其适应各种多目标函数并一定程度上提高了算法的鲁棒性。采用SBX[18]和DE[18]构建基于历史经验的自适应交叉算子选择策略。

为了构建基于历史经验的交叉算子选择策略，需对每一代循环使用的交叉算子进行计数索引处理，如SBX=2，DE=3。当种群初始化时，将两个交叉算子以1/2的概率随机分配给每个种群点。通过计算每一个存入外部存档的非支配解使用的交叉算子数量来表达两种交叉算子对种群进化的贡献程度，并采取遗传算法轮盘赌[19]的形式选出每一代的交叉算子对应的父代种群点。为避免某个交叉算子没有产生任何非支配解并存入外部存档中，应当设置最小选择概率下限Pmin。

2.3 特性约束映射修正策略

通过上述基于历史经验的自适应选择交叉算子策略产生的子代种群点通过映射条件约束扩展函数将不满足式（2）、（3）、（5）、（6）、（7）约束条件的可中断负荷、可转移负荷和充电负荷可控编码使其变为合格的可控编码，间接地扩大了算法决策变量可行域搜索范围，提升算法进化的多样性。具体约束映射修正策略如下：

（1）可中断负荷：当Ti,t,onTi,max,off时，将断电时间达到最大允许断电时间Ti,max,off后的控制编码置为1。

（2）可转移负荷：当Ti,on,tTi,conti,on时，将负荷运行达到需持续运行时间Ti,conti,on后的控制编码置为0。

（3）充电负荷：当充电汽车已经充满电时，将充满电后的控制编码置为0。

2.4 外部存档更新策略

算法中外部存档EP存储算法进化迭代过程中产生的非支配解，即为帕累托前沿近似值的输出集。外部存档更新机制直接导致算法输出值的好坏，更新机制效果较差可能导致较优的非支配解从外部存档中剔除或过多的非劣解占取大量的存储空间等问题。采用稀疏度[20]的方法剔除外部存档中的冗余非劣解，外部存档更新策略如下：

（1）当修正后的y′适应度值支配EP中非支配解时，则将y′存储到EP中，并将EP中被y′支配的解剔除。

（2）当修正后的y′与EP中的非支配解不存在支配关系，且EP没有达到存储上限，则将y′存入EP中。

（3）当EP达到存储上限，且修正后的y′与EP中的非支配解不存在支配关系；并y′适应度值的稀疏度大于EP中最小稀疏度解时，将y′替代EP中此最小稀疏度非劣解，当最小稀疏度解为多个时，将这些最小稀疏度解同时剔除，稀疏度公式如式（25）所示：

其中，fi为修正后子代点xi的适应度值，表示修正后子代点xi的第p维适应度值对应式（17）、（18）、（19），表示为EP中第i个解的p维适应度值，k表示距离修正解xi最近的k个EP中解的个数。

上述通过对MOEA/D作出一些改进，为了更直观地表达改进后算法的流程，详细给出AWS-MOEA/D算法流程如下。

Input：

根据电费、新能源丢弃率和用电峰谷差设计MOP

N：标量子问题数量（权重数量）

T：每个子问题包含权重向量的个数

G：循环终止条件

通过2.1节生成一组初始权重向量V1,V2,…,VN

Output：外部存档EP

步骤1初始化

步骤1.1设置外部存档

步骤1.2通过欧式距离计算出每个权重向量最近的T个权重向量，对于i=1,2,…,N，集合B(i)={i1,i2,…,iT}，其中为最近的T个权重向量

步骤1.3随机生成初始种群点{x1,x2,…,xN}作为负荷控制编码，并计算每一个xi适应度值对应的电费、新能源丢弃率和用电峰谷差f(xi)

步骤1.4初始化参考点1,2,3)

步骤2进化更新

步骤2.1自适应选择交叉算子并产生新的解y

步骤2.2映射条件约束扩展函数修正y得到y′

步骤2.3更新参考点z：对于每一维j=1,2,…,p，当fj(y′)

步骤2.4更新邻域解：对于j∈B(i)，当gte(y′|λj,z)≤gte(xj|λj,z)，将y′替代邻域内所有被y′支配的点

步骤2.5更新外部存档EP，并记录存入EP中非支配解的交叉算子个数

步骤2.5.1当F(y′)支配EP中解时，将y′存入EP，删除EP中被支配点

步骤2.5.2当EP没有达到存储上限，且y′与EP内非支配解不存在支配关系时，将y′存入EP中

步骤2.5.3当EP达到存储上限，则执行2.4节的稀疏度计算，将稀疏度小的种群点剔除，将y′存入EP

步骤3检查是否满足结束条件

步骤3.1若不满足则将此次循环存入EP中非支配解y′生成新的自适应权重向量，具体操作详见2.1节

步骤3.2满足循环终止条件时，输出EP

3 算例仿真分析

以某小区用户调度用电模拟调度效果。这里将1天的用电时间以15分钟为单位分为96个时间段，对普通居家类用户进行调度优化。基于实时电价[21]计算一天住户总用电电费，实时电价曲线图如图2所示。

图2 实时电价曲线图Fig.2 Real time electricity price curve

参与调度的各类负荷数据见表1~3。

表1 可中断负荷参数数据Table 1 Interruptible load parameter data

表1中设定了空调和热水器等可中断负荷的可调度时间范围和负荷运行时的运行功率。表2中微波炉需持续运行时间为5 min在优化时统一设定为最小变量15 min，并提供了可调度时间范围和负荷需持续运行时长。

表2 可转移负荷参数数据Table 2 Transferable load parameter data

表3为充电汽车与蓄电池的充电效率、充电功率，充电容量及其上下限参数，这些参数需满足式（9）、（10）、（11）、（14）等约束。

表3 充电储能负荷数据Table 3 Charging and energy storage load data

为了验证所改进的AWS-MOEA/D算法的有效性和优越性，将其与MOPSO、NSGA-II和MOEA/D进行收敛性和适应度值比较，算法参数都设置为种群100，迭代次数为200；NSGA-II算法中交叉概率为0.75，变异概率为0.01；MOPSO算法中惯性权重为0.73，学习因子均为1.495 1；MOEA/D和AWS-MOEA/D算法中邻域为10，外部存档为80，四种优化算法效果对比如图3所示。从图中可以看出AWS-MOEA/D适应度值最小并拥有较好的收敛效果；MOEA/D算法收敛效果较好，但没有达到预期的适应度值效果；MOPSO和NSGA-II适应度值效果都不满意，过早地陷入局部最优。

图3 四种优化算法效果对比Fig.3 Comparison of effects of four optimization algorithms

智能楼宇负荷调度算例仿真参数设置如下。设置最小选择交叉算子概率Pmin为0.1，稀疏度阈值k为5，邻域为20，种群数量设为200，迭代次数为500。目前，居民侧大都采用阶梯电价与实时电价，但该电价方式存在峰谷平时段交界处采用相同电价的不合理问题，而实时电价能够有效解决此问题。为充分验证实时电价进行调度的优越性，将实时电价与分时电价[22]在同一天的同类用户下进行调度实验，如图4所示。图中实线代表的实时电价在一天用总电趋势中整体较平缓，用电峰谷差相差不大，有效达到了削峰填谷的效果，并且在12：00到17：00高电价时段用电量在分时电价曲线之下；虽然分时电价在06：00到07：00之间降低了总体用电电量和增加了19：30到23：30之间的用电电量，但用电峰谷差较大，削峰填谷效果不显著。

图4 两种电价机制下用电量对比Fig.4 Comparison of electricity consumption under two electricity price mechanisms

将改进的AWS-MOEA/D算法分别与NSGA-II和MOEA/D算法在一天中用电调度情况进行对比，如图5所示，从图中可以看出：与其他两种算法调度结果相比，改进后的MOEA/D算法一天整体用电水平更低；在中午12点到下午16点高电价时段降低了用电电量；降低了夜间2：15、3：15、4：15和傍晚19：00、19：45时间点左右的用电量，此电量由白天蓄电池从新能源发电中存储的电量提供，间接地促进了新能源的消纳；NSGA-II算法调度结果在一天中用电量均呈现较高的水平，整体效果不佳；MOEA/D算法调度后用电量虽然在0：00点到2：15间减少了电网电量，但在上午11点到下午14点高电价时段用电量较多导致整体用电电费较高。

图5 三种算法调度后用电量对比Fig.5 Comparison of electricity consumption after dispatching in three algorithms

为说明一天中调度前后总用电量趋势，图6、7展示了居家类用户一天调度前后用电量对比，图中可以看出从上午10：00到下午16：30高电价期间用电量明显减少，这是因为由空调、热水器此类可中断负荷在用户能够承受的范围内间歇性中断用电和洗衣机、吸尘器和微波炉等可转移负荷的用电时段向相对较低电价时段平移造成的；相对增加了晚上20：00到24：00低电价时段的用电量，此用电时段主要是由蓄电池白天向新能源存储的电量和少量电网电量向电动汽车和家庭生活用电供电；凌晨0：00到早上8：00由于减少了空调和热水器此类大功率可中断负荷的用电时长造成了部分低用电量时段的产生。

图6 调度前日用电情况Fig.6 Daily power consumption before dispatching

图7 调度后日用电情况Fig.7 Daily power consumption after dispatching

图8~10分别表示可中断负荷、可转移负荷和充电负荷的典型大功率电器调度后的具体用电时段，图11为小区配备的一台储能电池总储能电量。从图8的空调调度后用电时段分布可以看出，空调减少了白天用电时长，傍晚19：00到早上5：00用电相对密集。图9中洗碗机的用电时段在用户能接受的范围内向相对较低电价时段平移。图10电动汽车用电量主要由白天储能电池充的电来供应，充电达到容量要求后停止充电。图11小区蓄电池电量由白天光伏清洁能源供应，其储存量在晚上19：00达到最大值，后续由于向家庭生活和充电汽车供电导致储存电量持续下降。