强噪声背景下钢丝绳损伤信号降噪方法

吴东， 张宝金， 刘伟新， 李光， 宫涛， 杨建华

(1.鞍钢集团矿业有限公司 眼前山分公司， 辽宁 鞍山 114044； 2.中国矿业大学 机电工程学院， 江苏 徐州 221116； 3.中国矿业大学 江苏省矿山机电装备重点实验室， 江苏 徐州 221116)

0 引言

钢丝绳作为一种柔性强、吸收冲击能力强的绳索类承载元件，在矿山、海港、船舶、桥梁等领域应用广泛[1]。在矿山领域，钢丝绳是矿井提升设备的关键承载部件，承载时变应力、载荷、扭矩等，在提升系统中有着十分重要的作用。但是钢丝绳工作环境恶劣，常面临潮湿、变载荷等工况，易发生磨损、断丝等故障[2]。一旦钢丝绳出现断丝，会导致断丝处承载能力差、抗疲劳能力减弱，极易发生钢丝绳整体断绳，造成大量经济损失甚至人员伤亡。因此，开展钢丝绳损伤检测与识别研究十分必要。

目前最常用、最可靠的钢丝绳损伤检测方法为电磁检测法[3]，其基本原理是利用静磁场沿钢丝绳轴向磁化钢丝绳，出现断丝的地方会产生向外扩散的漏磁，通过传感仪器收集漏磁信息，将钢丝绳断丝漏磁信息与正常磁通量信息进行对比，实现钢丝绳断丝损伤识别。该方法对钢丝绳损伤敏感，检测效果好。但是，由于实际工况中钢丝绳背景噪声很强，对损伤特征提取结果造成一定干扰，损伤特征信号提取困难。因此，钢丝绳损伤特征信号的降噪处理和特征提取成为亟待解决的难题。

钢丝绳损伤信号是一种非平稳无周期性的冲击信号，小波变换方法可以有效适应这种非平稳信号进而实现钢丝绳损伤信号分解、降噪等，在钢丝绳损伤信号处理中应用广泛[4-8]。但是，小波变换的效果严重依赖小波基及分解层数的选择，一旦小波基或者分解层数不适合，会在信号降噪的同时引入其他噪声干扰，影响信号处理与特征提取的效果。

相较于小波变换方法，移位平均法具有抗干扰能力强、信号适应性好、操作简单、计算量小等优点，只需要选择一定的移位窗宽即可实现对信号的有效降噪，因而被广泛应用于各类信号的降噪处理中。孙正宇等[9]提出了一种基于正态分布的滑动平均滤波法，可有效去除个别极端噪声数据，实现信号降噪处理。邵兴臣等[10]结合滑动均值算法和小波阈值降噪法有效地降低了噪声干扰，提取出叶间间隙信号。王龙等[11]针对钢丝绳损伤信号降噪问题，提出滑动平均结合小波阈值分析的算法，可实现钢丝绳损伤信号的自适应提取。但是上述研究中移位的窗宽需要人为选择，盲目性大。针对该问题，本文提出一种强噪声背景下钢丝绳损伤信号降噪方法。利用钢丝绳漏磁检测传感器采集不同类型的断丝数据，向信号中加入强高斯白噪声，以模拟强噪声背景；利用量子粒子群优化(Quantum Particle Swarm Optimization，QPSO)算法[12]优化移位平均法的窗宽，实现自适应参数选择与最优降噪输出。

1 高斯白噪声特性

高斯白噪声是信号处理中的一种常见噪声。钢丝绳在运行过程中由于各种因素不可避免地会产生摆动、振动等，这种振动情况是复杂且没有规律的，通常视为高斯白噪声[13]。

高斯白噪声概率密度服从正态分布，且功率谱密度为常数，满足以下统计特性：

(1)

式中：N(t)为高斯白噪声；t为时间;D为噪声强度；ξ(t)为均值为0、方差为1的标准高斯白噪声；〈N(t)〉为一阶矩，表示噪声的期望；〈N(t)，N(0)〉为二阶矩，表示噪声的均方值；δ(t)为狄拉克函数。

2 钢丝绳损伤信号降噪方法

移位平均法基本原理：将连续采样的信号序列中的一段看作为一个长度为L(即窗宽)的序列，将每次测量到的长度为L的序列中的首个数据去掉，其余L-1个数据依次向前移，从序列的最后一位开始插入新的采样数据。将L个数据相加并取算术平均值，以消除不规律波动等噪声的影响。移位平均法计算公式为

一是迅速摸清灾区水利设施受损情况。工作组到达地震灾区后要立即会同当地水利部门了解水利工程受损情况及可能出现的险情，落实排险避险措施，防止次生灾害造成重大损失。要组织有关专家分析地震前后卫星遥感图像和资料，研判是否存在堰塞湖险情；加强水文监测，分析水情变化和可能存在的风险。

(2)

式中：y(i)为处理后信号第i个点的幅值；x(i)为处理前信号第i个点的幅值。

窗宽的选择会直接影响移位平均法的处理结果，窗宽过大会导致截止频率过低，细节部分被忽略；窗宽过小会导致截止频率过高，降噪效果差。因此，本文提出自适应移位平均法，引入QPSO算法对移位的窗宽进行优化。将损伤信号的信噪比(Signal-to-Noise Ratio，SNR)作为适应度函数，通过QPSO算法使得SNR最大化，从而实现最优信号降噪效果。损伤信号SNR计算公式为

(3)

式中：i1为损伤信号起始点；i2为损伤信号终止点；M为损伤信号两侧的点数。

利用QPSO算法实现自适应移位平均法的流程如下：

(1) 初始化粒子种群，设置迭代次数为50，种群规模为50，初始化需要优化的参数L，同时设置窗宽的搜索范围为[5，500]。

(2) 通过式(3)计算各粒子的适应度值，作为初代粒子的最优位置适应度值Pb(i)，并将其中的最大值作为初代全局最优位置适应度值Pg。

(3) 更新粒子位置，计算每个粒子当前位置的适应度值，迭代更新个体最优位置适应度值Pb(i)和群体全局最优位置适应度值Pg。如果当前位置适应度值大于最优适应度值，则将当前位置适应度值作为最优适应度值，否则不改变最优适应度值。

(4) 若达到最大迭代次数50，则输出最优值；若不满足条件则返回步骤(3)重新计算。

3 实验及实测结果分析

3.1 实验准备

钢丝绳损伤检测实验台主要由Y66霍尔型便携式探伤仪、钢丝绳样绳(6×37S-FC，即钢丝绳有6股，每股有37根钢丝绳，绳芯为麻芯，直径为39 mm)、张紧装置、支撑装置等组成，如图1所示。

图1 钢丝绳损伤检测实验台Fig.1 Wire rope damage detection test bench

制作了4处不同程度的断丝损伤，其中2处相距0.24 m，另外2处相距0.15 m。推动便携式探伤仪在钢丝绳样绳上爬行，采集钢丝绳损伤信号。在实测信号中加入噪声强度D=3的高斯白噪声来模拟外界噪声干扰。

3.2 强噪声背景下平稳信号降噪实验结果

2处断丝损伤的检测信号如图2所示。该信号较平稳，但被噪声信号干扰严重，钢丝绳损伤判断受到很大限制。

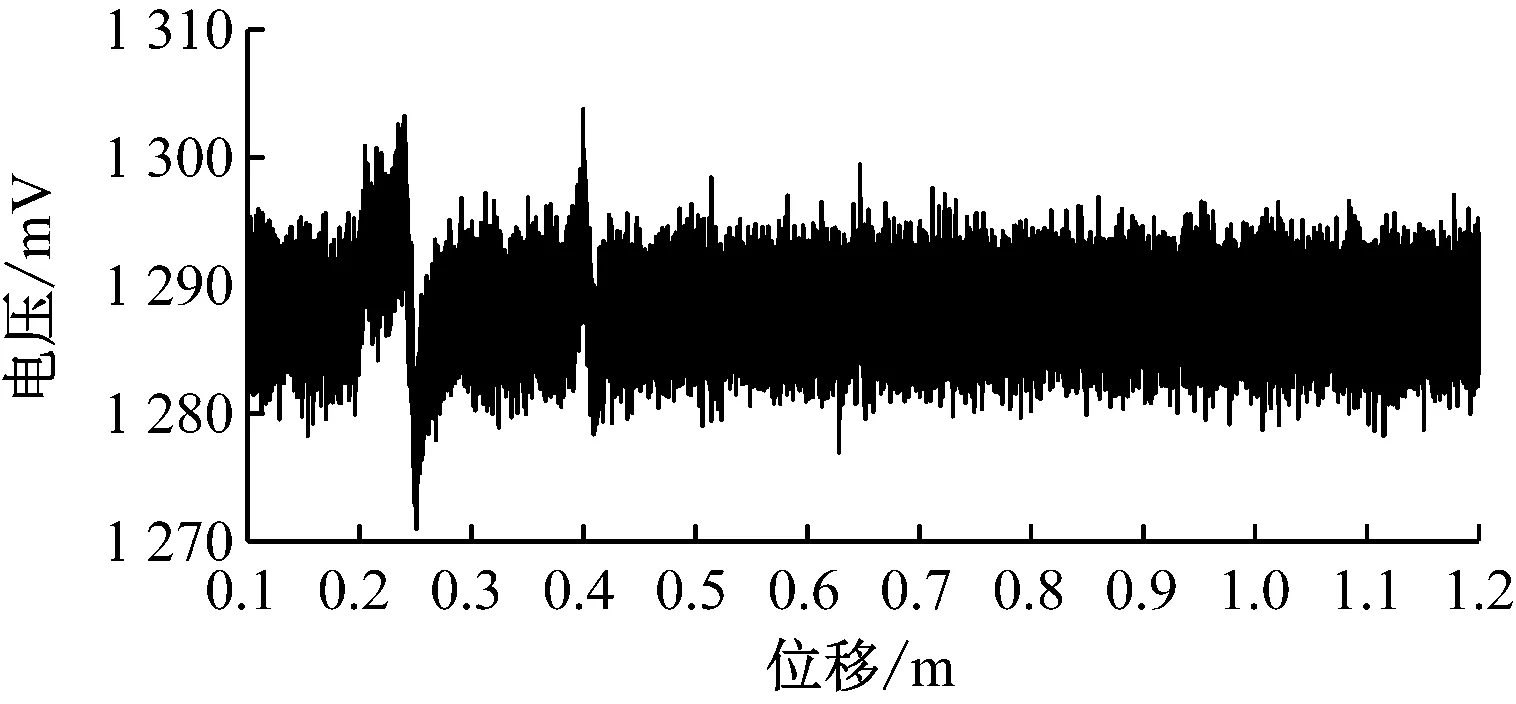
图2 被强噪声淹没的平稳信号Fig.2 Stationary signal submerged by strong noise

采用自适应移位平均法处理钢丝绳损伤信号，QPSO算法迭代曲线如图3所示。可以发现，迭代到第2次时SNR达到最大值-0.885 431 10 dB，此时寻优参数L=300.302 9。

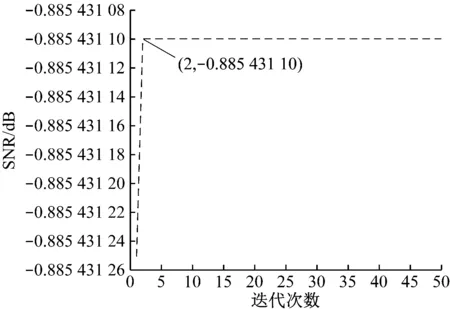
图3 处理平稳信号的QPSO算法迭代曲线Fig.3 Iterative curve of QPSO Algorithm for stationary signal processing

将自适应移位平均法与基于sym4的小波变换、基于db2的小波变换、基于db5的小波变换方法进行对比，结果如图4所示。其中2处损伤特征用虚线圆框标出，检测结果中2处损伤的距离约为0.24 m，与实验设置相符。从图4可知，采用自适应移位平均法处理后的钢丝绳损伤信号噪声干扰更小，信号更平滑，而采用3类小波基变换处理后的信号有一定的噪声干扰，在图4(b)中约1.0 m处甚至出现了强干扰。

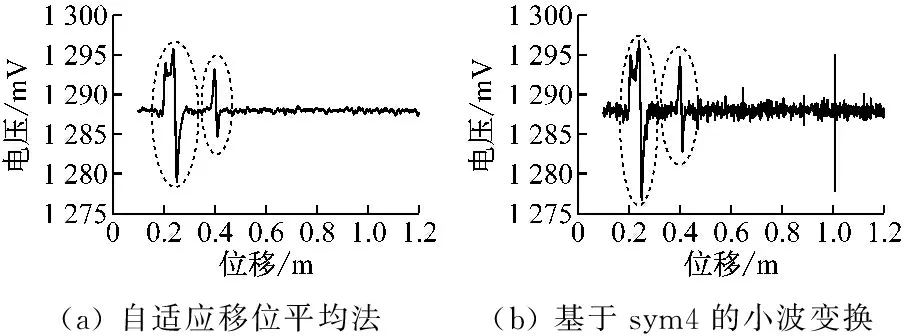
图4 平稳信号处理结果Fig.4 Stationary signal processing results

3.3 强噪声背景下波动信号降噪实验结果

另外2处损伤的检测信号如图5所示。该信号存在一定波动，这在实际检测中十分常见，可能是探伤仪速度波动、钢丝绳微弯等造成。

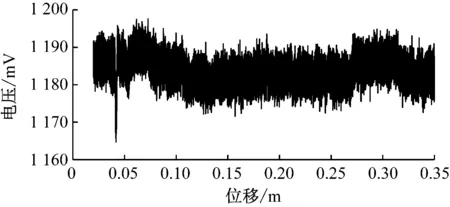
图5 被强噪声淹没的波动信号Fig.5 Fluctuating signal submerged by strong noise

采用自适应移位平均法处理损伤波动信号，QPSO算法迭代曲线如图6所示。可以发现，迭代到第5次时SNR达到最大值0.017 066 7 dB，此时寻优参数L=301.559 1。

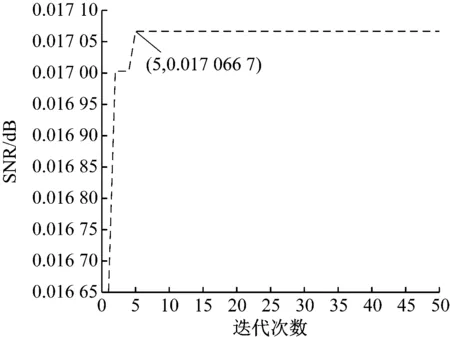
图6 处理波动信号的QPSO算法迭代曲线Fig.6 Iterative curve of QPSO Algorithm for fluctuating signal processing

自适应移位平均法、基于sym4的小波变换、基于db2的小波变换、基于db5的小波变换对波动信号的处理结果如图7所示。可见，检测结果中2处损伤的距离约为0.15 m，与实验设置相符。

图7 波动信号处理结果Fig.7 Fluctuating signal processing results

3.4 实测钢丝绳信号降噪结果

为了进一步说明所提方法的通用性，选取一段现场实测的提升机罐笼钢丝绳损伤信号进行验证。采样点数为4 000，该信号未经过算法处理，信号中含有明显的噪声，但相对较弱，如图8所示。

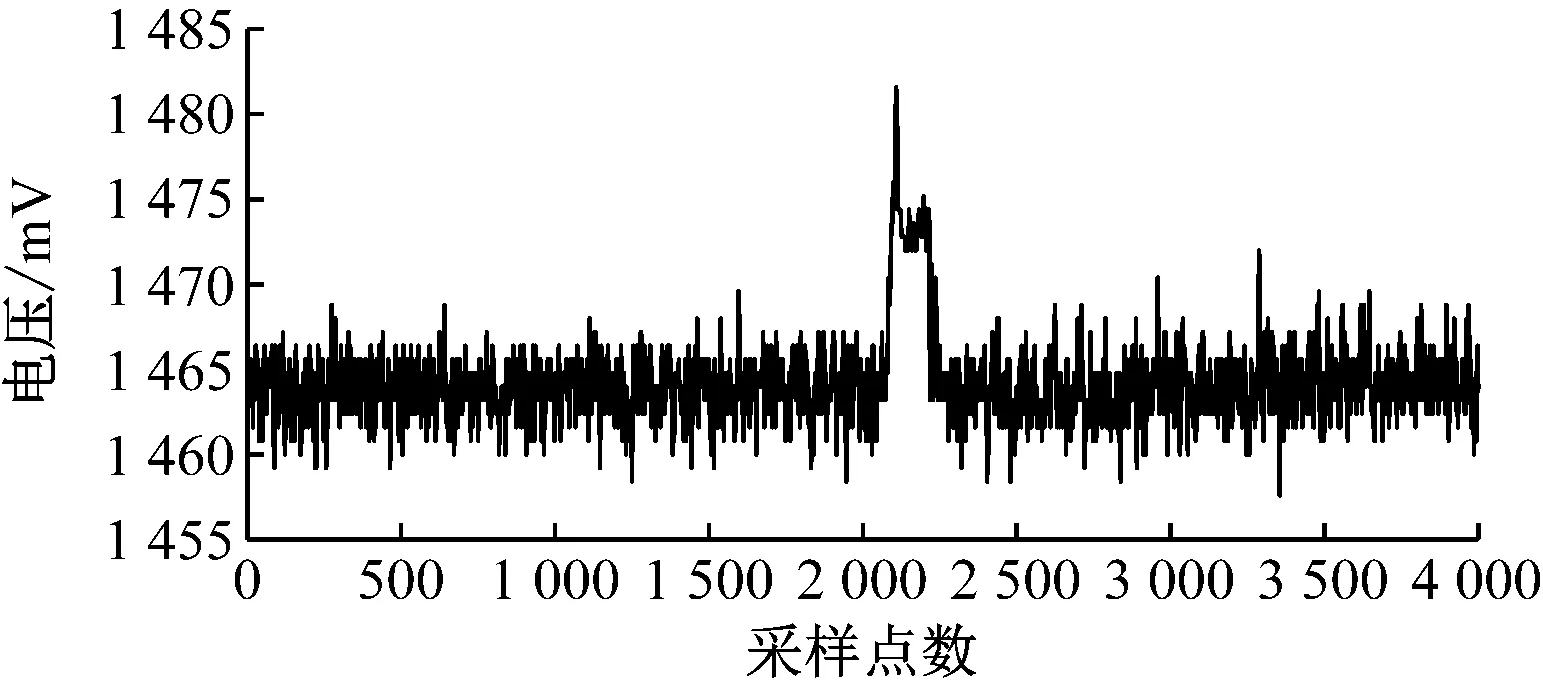
图8 现场实测钢丝绳损伤信号Fig.8 Measured wire rope damage signal on site

采用自适应移位平均法处理现场实测钢丝绳损伤信号，QPSO算法迭代曲线如图9所示。可以发现，迭代到第2次时SNR达到最大值3.633 137×10-7dB，此时寻优参数L=42.709 8。

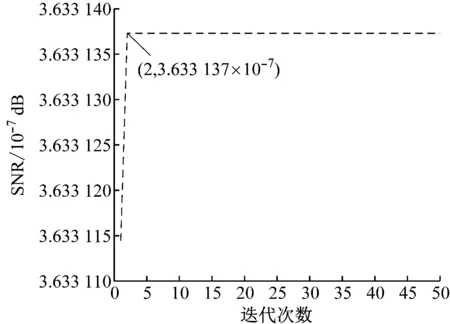
图9 处理实测信号的QPSO算法迭代曲线Fig.9 Iterative curve of QPSO Algorithm for measured signal processing

自适应移位平均法、基于sym4的小波变换、基于db2的小波变换、基于db5的小波变换对现场实测钢丝绳损伤信号的处理结果如图10所示。可看出本文方法处理后的信号更平滑，信号特征更突出。

图10 实测钢丝绳损伤信号处理结果Fig.10 Measured wire rope damage signal processing results

3.5 信号降噪结果对比分析

在平稳信号、波动信号、实测信号处理结果中，分别选取1处损伤特征的SNR进行对比，结果见表1。

表1 钢丝绳损伤信号处理结果对比Table 1 Comparison of processing results for wire rope damage signal

由图4、图7和表1可知，对于强噪声背景下的钢丝绳损伤信号，相较于小波变换，自适应移位平均法的降噪效果更明显，信噪比更高，信号更为平滑。同样，由图10可知，对于现场采集的噪声相对弱一些的信号，自适应移位平均法的降噪效果也比小波变换好。实验及实测结果表明，无论是在强噪声还是弱噪声背景下，自适应移位平均法均具有通用性，为进一步进行损伤信号识别与分类打下了基础。

4 结论

(1) 向钢丝绳损伤信号中加入强高斯白噪声模拟信号，模拟强噪声背景。采用自适应移位平均法实现强噪声背景下钢丝绳损伤信号降噪，通过QPSO算法选择最优窗宽，克服了人为选择窗宽造成的信号降噪效果差的缺点。

(2) 实验结果表明，对于强噪声背景下的平稳和波动信号，相较于小波变换，自适应移位平均法的降噪效果更明显，信噪比更高，信号更为平滑。

(3) 实测结果表明，对于现场采集的噪声相对弱一些的钢丝绳损伤信号，自适应移位平均法的降噪效果也比小波变换好，验证了自适应移位平均法具有较好的通用性。