基于激光测厚系统的精度补偿技术

郭国，赵慧，王称，何礼庆

天津轻工职业技术学院机械工程学院 天津 300350

1 序言

某特殊用途大型机械铝合金网格壁板，其长宽尺寸为5000mm×2500mm，网格壁板厚度范围为2～20mm。因板材需要较高的强度，且需要控制自身质量，所以设计人员对其厚度精度提出了较高的要求，厚度公差为±0.1mm。但由于板材尺寸较大，测量任务繁重，且精度要求较高，所以对传统人工手持超声测厚仪检测方法提出了较大的挑战。针对壁板厚度测量问题，引入双侧激光测厚技术，通过在壁板的两侧对称布置激光测距传感器，两传感器距离值分别与两传感器测距值求差，即可得到壁板的厚度值[1]。激光测量模块配合运动控制装置，可自动测量壁板的厚度。

激光测厚系统的核心部分是激光测量模块（见图1），该模块由一对激光线轮廓扫描传感器组成。因产品精度要求较高，所以设计人员对系统的检测精度提出了较高的要求，系统的静态误差（测量模块与壁板相对静止时的测量误差）应控制在±0.02mm以内。

图1 激光测量模块

该系统的原理并不复杂，但精度要求较高，在调试系统精度的过程中，存在如下问题：①系统的时间稳定性差，即从传感器通电开始，随着时间的推移，测量结果也随之变化（漂移），需要等待较长的时间，传感器才能提供稳定的测量数据。②传感器存在明显的线性误差，导致检测不同厚度的壁板时，测量精度差别较大。针对上述问题，需要对传感器进行修正补偿，提升系统的稳定性和测量精度，以满足设计要求。

2 系统测厚原理

系统所使用的传感器为某进口激光线轮廓扫描传感器，传感器的工作原理是基于激光三角测距法[2]，光路如图2所示。

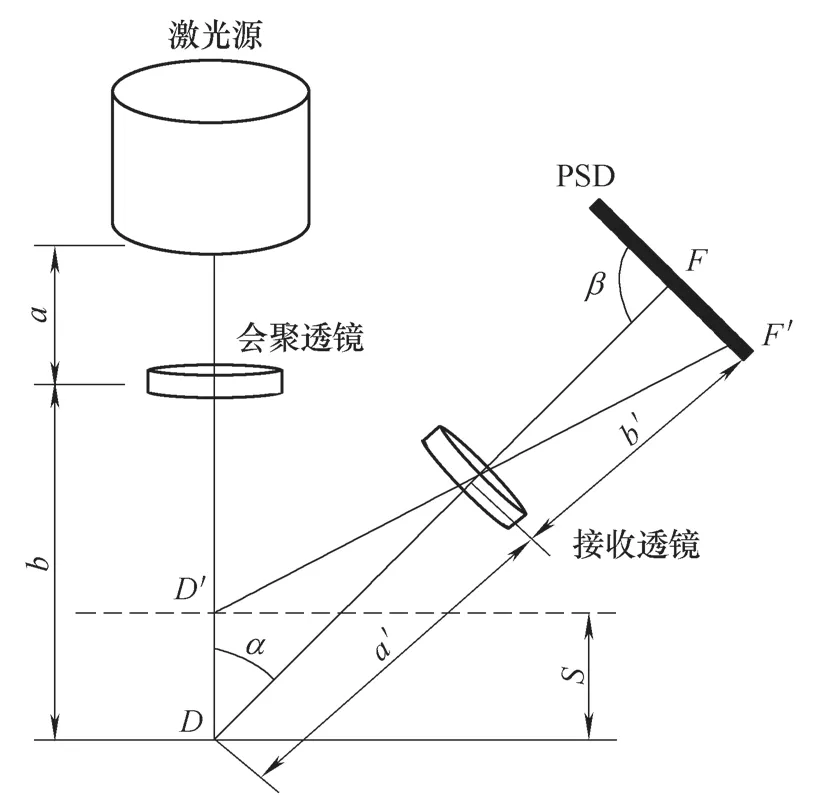
图2 激光三角测距法光路

该传感器的组成主要包括激光源、会聚透镜、接收透镜、探测器（主要是PSD或CCD）及信号处理控制器等。由激光光源发出的激光经会聚透镜到达被测产品的表面，其漫反射光经接收透镜形成光斑，并成像在光电检测器件（PSD）上。该散射光斑的中心位置由传感器与被测物体表面之间的距离决定。被测物体表面的位移改变会使光敏元件上成像光点发生位移，而光电检测器件输出的电信号与光斑的中心位置有关，通过对光电检测器件输出的电信号进行运算处理，就可获得传感器与被测物体表面之间的距离信息[3]。假设当物体位于参考面D时，光斑成像于PSD中心位置F处，被测面与参考面相距S时，光斑像点在PSD上的位移为△S，其中△S=FF'。则S为

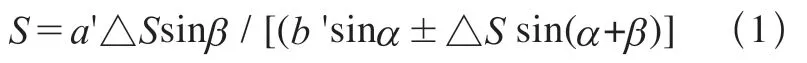
该传感器可实时测量与被测物体表面之间的距离。本系统所使用的激光线轮廓扫描传感器如图3所示。Z方向为传感器的测距方向，量程为80～120mm，即传感器与被测产品之间的距离应控制在Z方向量程内。X方向量程为50mm，即传感器在X方向扫描测量范围为50mm的线。

图3 激光线轮廓扫描传感器

在被测壁板两侧同时安装该传感器，使壁板处于两传感器Z方向工作量程内，预先标定两传感器的距离L，L与两传感器的测距值求差值，即可实现壁板厚度的测量。

3 传感器时间稳定性（漂移）补偿

3.1 问题分析

传感器的时间稳定性较差，即从传感器通电开始，不同时间对同一产品的同一位置进行测量，测量结果存在较大差异。测量现场为恒温、无振动环境，排除了外界环境的影响。为了获得传感器示值随时间的变化规律，进行了相关的试验。

因传感器Z方向工作量程为80～120mm，需要研究传感器在全量程内的示值变化规律。从传感器通电开始，持续跟踪观测传感器Z方向80mm和120mm两个静态目标，观测时长为7200s，分别得到两组示值变化曲线。以传感器1为例，所得数据曲线如图4所示。

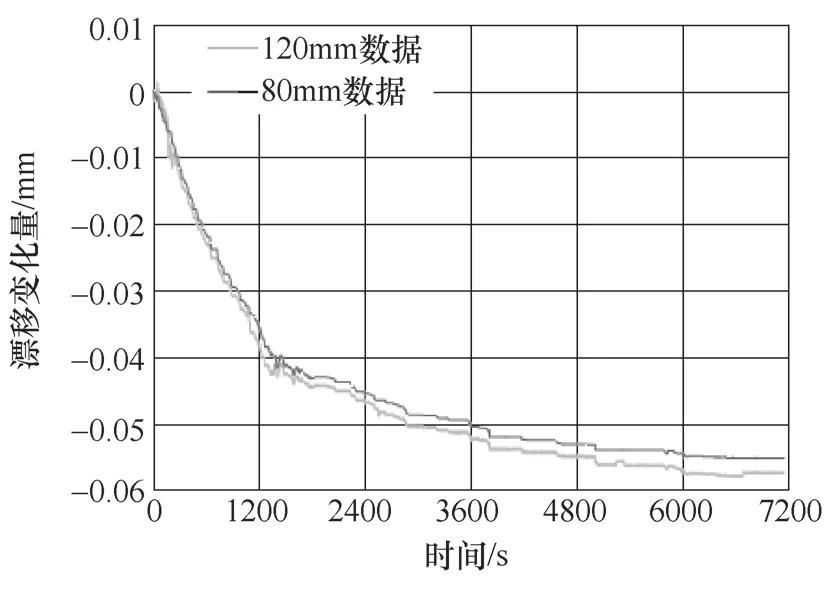
图4 传感器1示值变化曲线

从图4中可获得三点信息：①传感器从开机通电至6000s，传感器示值变化量＞0.05mm，若不增加补偿措施，此时间段传感器难以满足使用要求。②6000s后，两组数据均趋于稳定，最终数值稳定在±0.001mm以内，可以满足使用要求。③两组数据的变化趋势一致，传感器在量程范围内的一致性较好，且稳定状态下（6000s后），两组数据的差值为0.0024mm，有利于对传感器进行补偿。

综上所述，传感器开机通电后，需要等待6000s才能使用，难以满足现场使用要求。需要通过增加补偿措施，缩短传感器从通电到稳定状态所需等待的时长，减小漂移量，提高传感器的时间稳定性，使传感器尽快进入稳定工作状态。

3.2 时间稳定性（漂移）补偿

针对传感器时间稳定性问题，通过硬件和软件算法相结合的方法进行补偿。

（1）补偿原理 以传感器1为例，在传感器Z方向量程下限位置安装一个高精度的补偿板，传感器与补偿板之间的距离记为Zmin，如图5所示。该补偿板为100mm×50mm的矩形薄板，薄板中间部分均匀去掉90mm×40mm的矩形，保证传感器工作时，激光线中间40mm可以透过补偿板投射到被测产品上，用于测量距离。两侧5mm激光线被补偿板阻挡，用于补偿[4]。

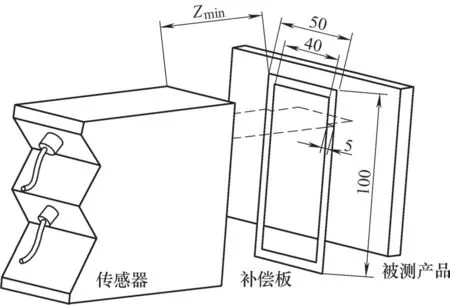
图5 补偿示意

在传感器进入稳定工作状态后（传感器通电6000s之后），读取Zmin处补偿板的距离值，记为Zref，Zref为Zmin处的参考值。从传感器开机通电开始，在任意时刻读取补偿板的值为Zcomp，Zmin处该时刻的实时补偿值记为△fmin，则

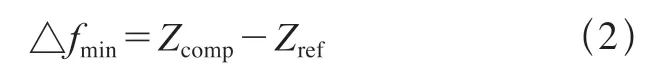
需要注意，在传感器量程下限Zmin和上限Zmax处，稳定后二者示值存在0.0024mm的偏差量，Zmin处的实时补偿值△fmin不能直接用于补偿全量程范围内的误差值，需要增加补偿修正值。为了方便获得量程内的修正值，此处采用了简化求法，将0.0024mm在全量程内进行线性化分布处理，作为任意位置的修正值，记为△fmod。用Zobj表示传感器在任意时刻获取的壁板测量值，则△fmod为

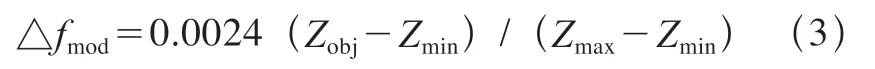
结合式（2）和式（3），可推算出被测目标在传感器进行时间稳定性（漂移）补偿后的数值Ztime

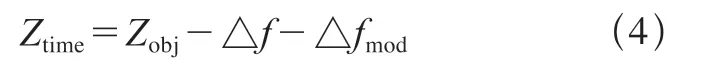
（2）方案实施 传感器1和2在Z方向量程下限处增加补偿板，如图6所示。并将式（2）、式（3）和式（4）加入到算法中进行补偿，用于改善系统的时间稳定性（漂移）。

图6 传感器增加补偿板

（3）补偿结果 对补偿后的测量结果进行验证，从传感器1和传感器2开机通电开始，持续跟踪观察某一静态目标至7000s，两传感器的示值变化情况分别如图7和图8所示。

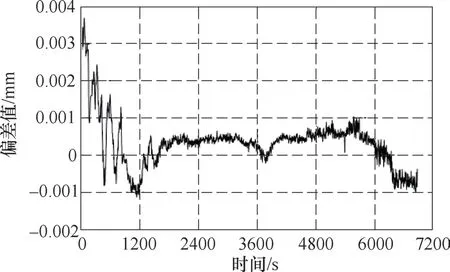
图7 传感器1示值变化情况

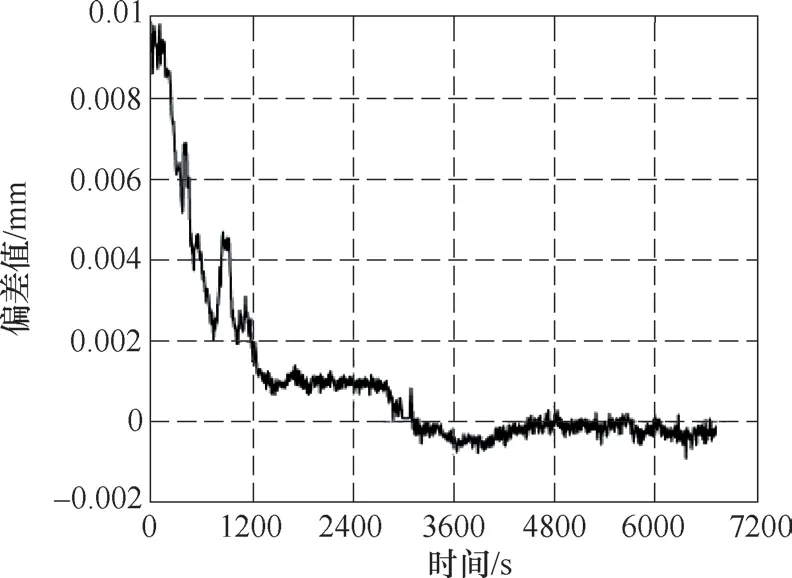
图8 传感器2示值变化情况

由图7和8可知，两传感器均在开机通电1200s后进入稳定工作状态，数据波动量在±0.001mm范围内。与加入补偿之前相比，系统提前了4800s进入稳定阶段，取得了不错的效果。

4 传感器线性误差补偿

4.1 问题描述

因被测壁板的厚度范围为2～20mm，且壁板存在弯曲变形等问题，为了保证系统在上述条件下具有较高的精度，要求传感器在全量程内应具有较好的线性度。

在传感器稳定工作状态下（开机通电1200s之后），将被测样件置于带有高精度光栅尺（精度2μm/m，分辨率0.001μm）的移动机构上，通过对传感器1和传感器2在全量程内进行观测，并与光栅尺示值对比，分别得到两传感器在全量程内的线性误差，如图9所示，横坐标为光栅尺示值，纵坐标为传感器与光栅示值的偏差值。由图9可知，两传感器在全量程内线性误差较大，难以满足使用要求，需要对线性误差进行补偿。

另外，在全量程内对两个传感器进行重复测量试验，两传感器的重复测量误差均＜0.003mm，重复性较好，有利于对传感器进行线性误差补偿。

4.2 线性误差补偿

（1）补偿原理和方法 通过对图9所示的偏差值数据进行换算，得到传感器示值与线性误差补偿值的分段函数图（相邻两点之间用直线连接），如图10所示。图10横坐标为传感器示值，纵坐标为传感器对应的线性误差补偿值，记为△flin。在传感器的量程范围内，对于任意距离的测量值，均可通过图10函数曲线得到对应的线性误差补偿值△flin。将其加入到算法中进行补偿，可以得到线性误差补偿后的测量结果[5]。经过线性误差补偿后的传感器示值记为Zlin

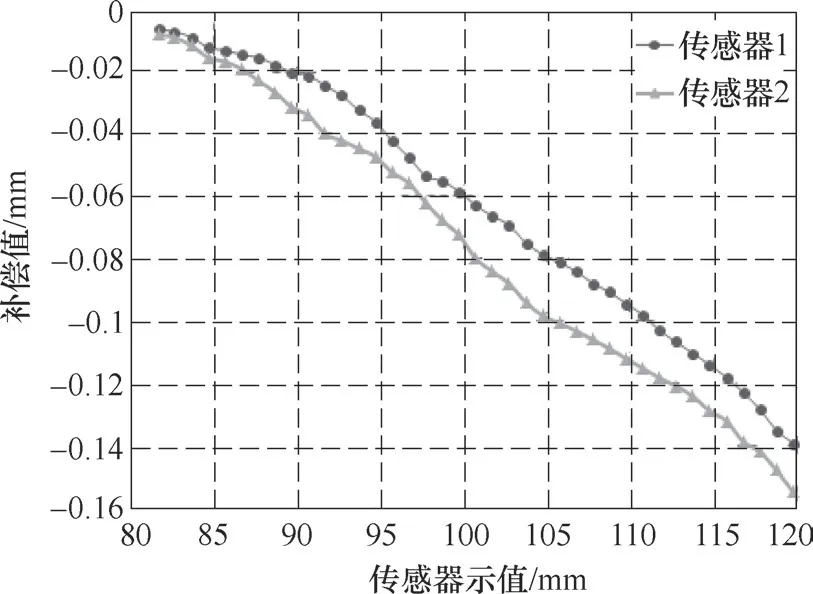
图10 传感器示值与补偿值分段函数曲线

（2）线性误差补偿结果 对经过线性误差补偿的传感器进行测试，与光栅尺示值进行对比，得到两传感器在全量程内的线性误差，如图11所示。由图11可知，两传感器的偏差值均在±0.006mm以内。

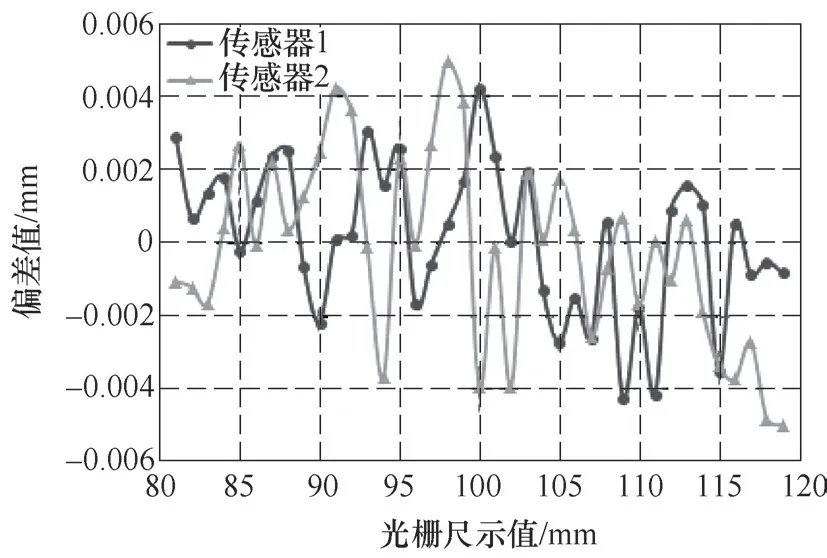
图11 补偿后传感器线性误差

5 测量结果评定

5.1 标定两传感器的距离值

标定两传感器的距离值如图12所示，将标准样板置于两传感器的中间位置，使标准样板同时处于两传感器Z方向工作量程内。将样板的厚度与两传感器的示值进行求和，获得两传感器的距离值Lcalib=200.102mm。

图12 标定两传感器的距离值

传感器1和传感器2经过漂移补偿和线性误差补偿后的测量值分别记为Zlin1和Zlin2，则被测壁板的厚度h为

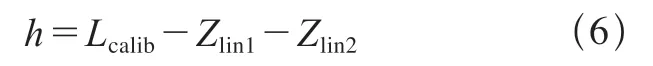
5.2 厚度测量结果评定

在静态条件下，即传感器与被测壁板样件相对静止时，将样件置于系统量程内，应用该测厚系统检测壁板样件，进行静态测量试验[6]，如图13所示。以开机时间和壁板样件厚度为变量，获取多组测量数据，并与三坐标测量机检测结果进行对比，数据见表1，以验证系统的稳定性和精度[7]。由表1可知，系统静态测量误差控制在±0.018mm以内。

图13 静态测量试验

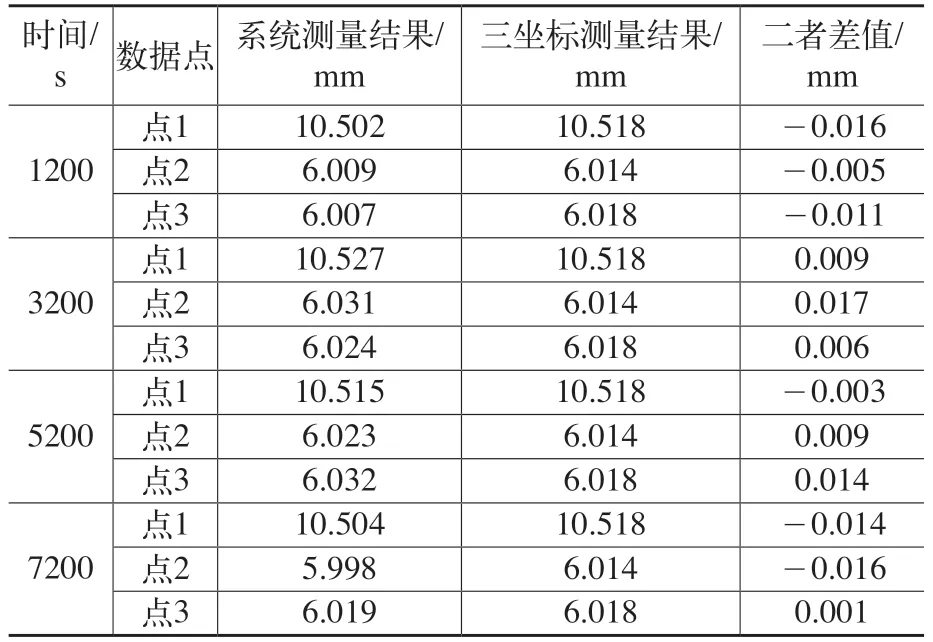
表1 厚度测量对比数据

6 结束语

本文通过开展传感器时间稳定性（漂移）补偿、线性误差补偿及传感器距离标定等试验，缩短了传感器进入稳定工作状态所需时长，提高了系统检测精度。通过开展静态测量试验，验证得测量误差在±0.018mm以内，满足设计要求的±0.02mm，取得了理想的效果，为工程技术人员解决此类问题提供了有效的参考。