基于灰色-尖点突变理论的钢筋混凝土Ⅰ-Ⅱ复合型断裂过程分析

2022-01-25巩妮娜胡少伟范向前蔡小宁

建筑材料学报 2022年1期

巩妮娜，胡少伟，范向前，蔡小宁

（1.江苏海洋大学土木与港海工程学院，江苏连云港 222005；2.河海大学力学与材料学院，江苏南京 210098；3.重庆大学土木工程学院，重庆 400045；4.南京水利科学研究院，江苏南京 210029）

钢筋混凝土的受力特性与裂缝发展密切相关，其断裂过程的定量描述是一个基础性课题.钢筋的限裂作用使混凝土结构破坏前具有相对缓慢的裂缝稳定扩展阶段，因而其断裂行为与素混凝土有明显差异.结构裂缝多处于弯剪复合应力场中，因此钢筋混凝土Ⅰ-Ⅱ复合型断裂过程的研究对于大型结构的损伤预报和安全性评价具有重要的意义.声发射是材料内部快速释放应变能从而产生弹性波的现象［1］，文献［2-3］分析了混凝土断裂过程的声发射特征，指出声发射参量能够识别裂缝扩展过程的临界点.文献［4-5］采用平均频率（AF），上升时间/幅值（RA）等参量表征不同类型混凝土的损伤破坏过程.Soulioti等［6］发现声发射活动性与纤维含量及材料韧度基本成正比.Dev等［7］指出声发射事件定位结果能够表征纤维混凝土梁的裂缝扩展路径.任正义［8］提出声发射损伤定位的优化方法，降低了传统定位方式的误差.

灰色系统理论［9］通过对“小样本”、“贫信息”等原始系统进行数据处理，寻找某段时间内的规律从而进行灰色预测.Thom创立的突变理论［10］可以研究损伤过程中的突变不连续现象，其中尖点突变理论［11-12］形式简单，应用最为广泛.周煜［13］利用灰色理论和突变理论分析混凝土梁断裂过程的声发射信号并确定了临界荷载.陈迪辉等［14］引入尖点突变理论对拱坝安全度进行定量评估，发现其与传统方法的结果相吻合.

目前混凝土Ⅰ型断裂的研究成果较为丰富，而钢筋混凝土Ⅰ-Ⅱ复合型断裂过程的研究尚不多见.本文同步采集断裂过程的声发射信号，基于灰色-尖点突变理论识别系统的突变点，进而分析Ⅰ-Ⅱ复合型裂缝的扩展过程.

1 基于声发射参量的灰色-尖点突变理论

1.1 灰色理论

钢筋混凝土Ⅰ-Ⅱ复合型断裂的过程中，裂缝开裂与扩展的突变行为会导致声发射信号的突变，因此分析声发射过程的突变特征对于描述断裂过程有重要意义.灰色理论通过对“已知”信息进行处理，减少其随机性从而提升信息的确定性，达到对原有数据进行准确拟合的目标［15］.由于断裂过程中直接获取的声发射信号具有一定的随机性，采用灰色累加的方法可以使得数据序列呈现单调增加趋势，更具有序性，因此选取适当的声发射参数构造一个原始序列x（0）［9］：

对式（1）序列进行一次累加，得到Accumulated generating operation（AGO）序列：

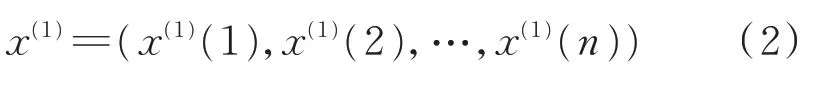
1.2 尖点突变理论

试验表明，钢筋混凝土的损伤断裂过程存在临界状态，而突变理论正适用于描述这类非连续现象.Zeeman提出的尖点突变理论具有1个状态变量x、2个控制变量u、v，其势函数V（x）为［11］：

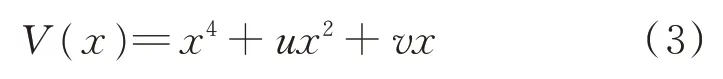
对式（3）求一阶导数得到平衡曲面方程，如图1所示［1］：

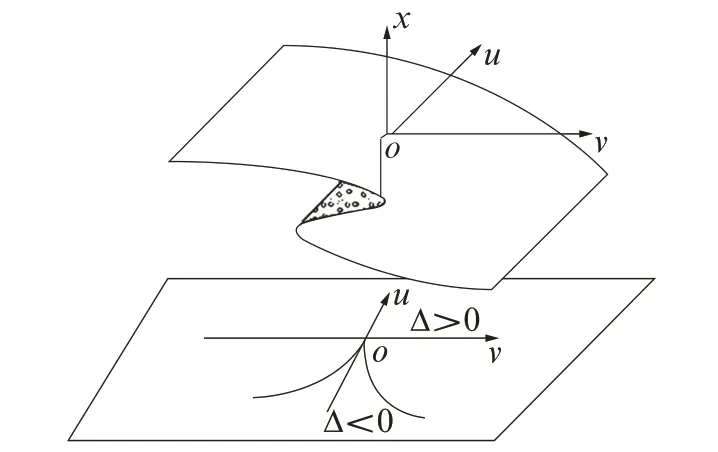
图1 平衡曲面及分叉集Fig.1 Equilibrium surface and bifurcation sets

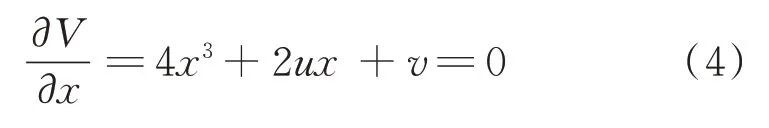
将平衡曲面向u-o-v平面投影，得到分叉集，可由式（4）平衡曲面方程和式（3）二阶导数为零，联立求得特征值：

平衡曲面包括上、中、下叶，设M（u，v，x）为表示系统状态的点，当其沿着上叶、下叶移动时，u、v的平稳变化引起x的平稳变化，即系统稳定；当M点运动轨迹穿过分叉集，位于平衡曲面褶皱处的中叶时，u、v的微小变化即引起M点的突跳，从而导致x的突变［16］.分叉集将控制平面分为不同区域，以特征值Δ表征的判别准则如下［12］：

1.3 基于声发射参量的灰色-尖点突变模型

由于试验测得的振铃计数等过程参量中各数据点的时间间隔有差异，为了消除非等间隔的影响，选择振铃计数率x与撞击数n的关系作为初始序列x(0)，采用式（2）对该序列进行一次累加，得到AGO序列x(1)，将生成序列x(1)展开成幂级数的形式，并截取前5项，则得到x(1)的近似表达形式［1］：

其中A0、A1、…、A5为待定系数，可通过多项式拟合方法来确定，对式（7）求导得到还原后的声发射参量序列：

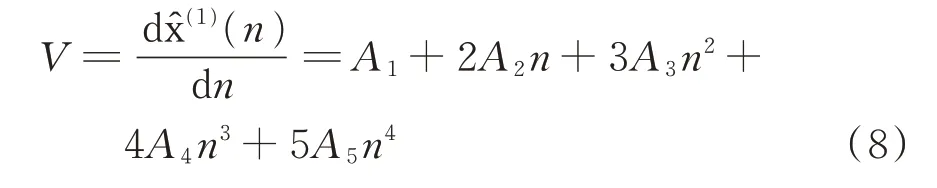
令a0＝A1，a1＝2A2，a2＝3A3，a3＝4A4，a4＝5A5，利用参数代换将式（8）构造为标准势函数表达形式，令n＝Z－q（a4＜0），q＝，可得［14］：

当a4＞0时，V(z)＝z4+uz2+vz+w（9）式中：u＝.

当a4＜0时，V(z)＝－z4－uz2－vz+w（10）式中：. 其中k1＝－4q3a4+3q2a3－2qa2+a1，k2＝6q2a4－3qa3+a2.

式（9）、（10）中，w为剪切项，对突变分析无影响，可忽略.由尖点突变理论可知，分叉集方程形式为式（5），当Δ＜0时，系统产生突变.

2 钢筋混凝土Ⅰ-Ⅱ复合型断裂过程分析

2.1 试验概况

为了判断钢筋混凝土Ⅰ-Ⅱ复合型断裂过程的突变点，以DL/T 5332—2005《水工混凝土断裂试验规程》推荐的三点弯试件为基础，通过调整其裂缝位置使裂尖处于弯拉复合应力场.直偏裂缝三点弯曲梁的尺寸（L×B×H）为1 000 mm×120 mm×200 mm，跨间尺寸800 mm，预制裂缝偏离跨中160 mm，初始缝高比为80/200＝0.4，试件具体参数见图2.混凝土配合比取m（水泥）∶m（水）∶m（砂）∶m（石子）＝1.000∶0.440∶1.367∶2.907，其中水泥为P·O 42.5普通硅酸盐水泥，采用同批次混凝土浇筑棱柱体试块150 mm×150 mm×300 mm测得轴向抗压强度为36.50 MPa.底部配置2根直径为6.5 mm的HPB300光圆钢筋，配筋率为0.276%，保护层取25 mm.按照试件尺寸预制木模板，将纵向钢筋绑扎固定，采用尖端V型厚度约3 mm的不锈钢板插入模板相应位置以形成预制裂缝，混凝土初凝后拔出钢板，室内常规养护28 d.

由于混凝土Ⅰ-Ⅱ复合型断裂过程中会出现跨中底部和裂缝尖端2个薄弱位置［3］，本试验在混凝土表面粘贴了2组应变片：裂尖两侧布置2个应变片，以裂尖和加载点连一直线，垂直于直线方向相等间隔布置4个应变片，其中应变片1、2、3用来检测裂尖起裂荷载，应变片4、5、6监测裂缝发展过程；为了获得跨中开裂荷载，在跨中底部粘贴2个应变片7、8，应变片布置如图2所示.

本试验在500 t的三轴压力试验机上进行，主要采集数据为：荷载P，裂缝开口位移，应变值ε等，其中荷载P采用荷载传感器测量，通过连续采集模式将数据传至数据采集与控制系统.采用美国声学物理公司研发的8通道声发射系统开展声发射试验，在加载前采用砂纸打磨布设传感器的混凝土表面使其光滑，涂抹凡士林以确保传感器与试件表面接触良好，将4个声发射探头通过胶带固定在试件前后表面形成空间定位，探头距试件上下底面均为50 mm，试验中前置增益设为40 dB，滤波频率设为1～60 kHz，探头布置情况见图2，其中实线圈和虚线圈分别表示在试件正面和背面布置的声发射传感器.

图2 直偏裂缝三点弯曲梁Fig.2 Three-point bending beam with a straight offset notch（size：mm）

2.2 声发射参量时程分析

直偏裂缝三点弯曲梁的起裂荷载通过裂尖附近粘贴应变片的应变-时间（ε-t）曲线的转折点获得.随着加载进行，裂尖附近能量聚集，应变值逐渐增大，当达到起裂荷载时，裂缝尖端起裂，此处的能量释放，附近应变片1、2、3的应变值减小［17］，此时即为起裂点，如图3中A点所示.同理，跨中底部开裂荷载也通过应变片7、8的应变值回缩点来确定，如图3中B点所示.达到图3中C点后，荷载-时间（P-t）曲线出现小幅下降，可视为试件首次出现失稳扩展［18］，该临界荷载记为Pc.由于钢筋的存在，P-t曲线的峰后阶段变得平缓，裂缝扩展速率得以抑制，随后荷载逐渐恢复甚至超过临界荷载Pc，说明钢筋的加入控制了失稳扩展并提升了构件承载力.

图3为能量释放率与荷载时程曲线.图4为振铃计数与荷载时程曲线.由于加载初期经历了加载装置与试件接触、逐渐压密等事件，外部环境对声发射信号产生较大影响，因此本文从140 s开始统计.由图3可见：在裂尖起裂时刻，能量释放率并未表现出明显的突变行为，而在跨中开裂B点和临界状态C点时有较为明显的突增.跨中开裂后，随着加载的进行，损伤加剧，同时混凝土承担的荷载逐渐转移至钢筋，二者交替承载不断形成新的平衡，从B点至C点之间能量释放率也出现了若干次峰值，其最大值甚至超出B点和C点的对应值，说明这一阶段声发射活动性显著增强，且跨中开裂B对应的能量释放率接近2.5×106，大于临界状态C点的数值，即跨中开裂是断裂过程中一个重要的临界点.图4中振铃计数与能量释放率具有类似的特征，但能量释放率在B点和C点的突变行为更加明显.

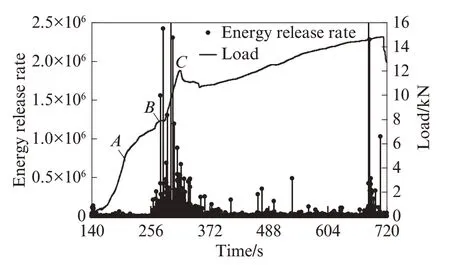
图3 能量释放率与荷载时程曲线Fig.3 Time history curve of energy release rate and load

图4 振铃计数与荷载时程曲线Fig.4 Time history curves of AE ringing counting and load

2.3 基于灰色-尖点突变理论的断裂过程分析

选取振铃计数率按照1.3所述方法计算所得特征值Δ的绝对值较大，为了更加清楚地在图中表达其正负特征，定义突变指标Δ′如式（11）所示，Δ′与Δ正负相同，但绝对值减小：

根据上述方法对裂缝扩展过程中不同时刻的突变指标Δ′进行计算，时间间隔取50 s，临界时刻附近适当加密，将560 s之前的计算结果列于表1，其余时刻的结果见图5～7.

表1 裂缝扩展不同时刻的突变指标Table 1 Catastrophe index at different moments of crack propagation

图5为突变指标Δ′与裂尖处应变时程曲线.由图5可见，当t＝203 s时，裂尖附近应变片的ε-t曲线出现回缩，即裂尖起裂，对应于这一时刻Δ′为－14.99，第1次出现负值，表示系统不稳定，发生突变.

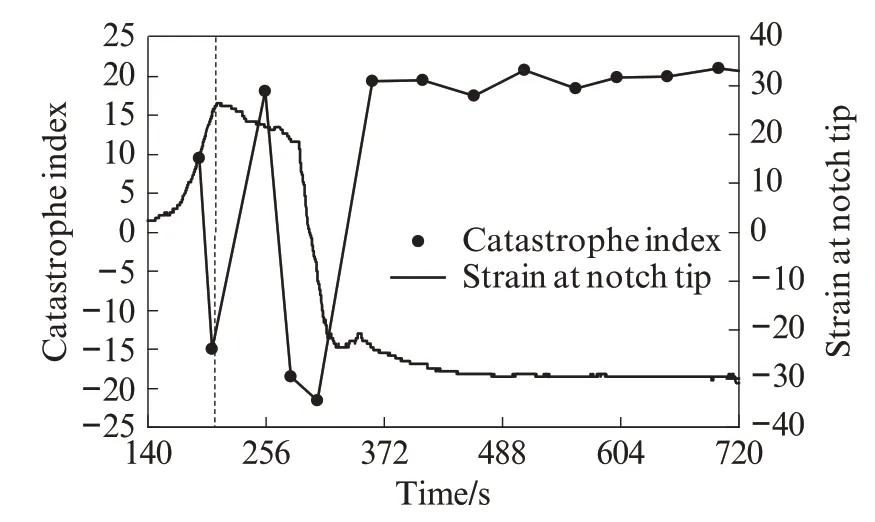
图5 突变指标与裂尖处应变时程曲线Fig.5 Time history curve of catastrophe index and strain at notch tip

图6为突变指标Δ′与跨中应变时程曲线.由图6可见，在280 s附近，跨中附近应变片的ε-t曲线出现明显回缩，即跨中开裂，该时刻的Δ′为－18.54，第2次出现突变.

图6 突变指标与跨中底部应变时程曲线Fig.6 Time history curve of catastrophe index and strain at midspan

图7为突变指标Δ′与荷载时程曲线.由图7可见，在306 s附近荷载达到Pc，随后出现小幅下降，对应于此时刻的Δ′为－21.62，出现第3次突变.计算过程发现当t取765 s时，Δ′亦出现负值，但此时试件已发生破坏，此处不再讨论.同时分析预制裂缝位置和跨中位置处的钢筋应变可知，从裂尖起裂至跨中开裂阶段，钢筋应力近似线性增长，从跨中开裂起线性增长速度变快，到达临界荷载Pc后，钢筋应力突增随后达到屈服，如前所述，荷载出现小幅下降后逐渐回升，由于钢筋应力强化使得荷载在后期可能超过Pc，钢筋的加入提升了构件的承载能力.

图7 突变指标与荷载时程曲线Fig.7 Time history curve of catastrophe index and load

如2.2所述，能量释放率和振铃计数在裂尖起裂时刻均未表现出明显的突变特征，而基于振铃计数率的灰色-尖点突变模型能够有效的识别裂尖起裂、跨中开裂和Pc等3个临界时刻，在此基础上可将裂尖起裂与临界荷载Pc之间的断裂过程视为裂缝稳定扩展阶段，这一模型可作为声发射基本参量分析方法的有益补充.

图8为试件破坏图，试件的宏观破坏路径表现为起始于裂尖的复合型斜裂缝（如红色线条所示）.图9为加载初期和试件破坏时的声发射事件三维定位图，蓝色线框示意预制裂缝.由图9可见：在加载初期出现少量损伤点（图9（a）），并主要存在于跨中底部，这是由于跨中底部承受最大弯矩亦是薄弱部位，钢筋在加载初期对于预制裂缝有限裂作用；试件破坏时大量的损伤点同时出现在复合型斜裂缝（路径Ⅰ）周围和跨中底部附近（路径Ⅱ）（图9（b））.这一现象表明，虽然试件的跨中底部并未形成可见的宏观裂缝，但在加载过程中内部已产生大量的损伤，基于振铃计数率的灰色-尖点突变模型能够有效地识别出跨中这一薄弱部位的开裂时刻，该分析方法可为大型结构裂缝稳定性分析和预警监测系统建立提供基础.