螺旋槽对自适应迷宫密封的影响研究*

赵炬颖 陈 义 祝天一 徐乙人 祁志浩 李永健

(1.清华大学摩擦学国家重点实验室 北京 100084； 2.西安电子科技大学机电工程学院 陕西西安 710071 )

燃油系统是航空发动机各工作系统中最为复杂、重要的系统之一，是发动机控制的核心。燃油泵则是燃油系统的核心，起到给燃烧室供应燃料、驱动多种执行机构的作用，其工作能力和可靠性对航空发动机的工作性能和安全性能具有重要影响。而密封又是其中不可或缺的一环，其中一种较为常见的密封形式就是迷宫(篦齿)密封。

迷宫密封是一种工业上较为常见的非接触密封形式，它具有结构简单、方便使用、易于维修等特点，被广泛应用于航空发动机中，起到了防止工作介质泄漏、提升设备运转效率的重要作用[1-3]。其密封原理是密封齿与转轴之间形成了一系列节流间隙和膨胀空腔，当泄漏流体流经节流间隙时，其部分压力转换为流体的速度，但由于膨胀空腔的作用，流体的速度无法再转换为流体的压力，而是转换为热能耗散，从而使得流体压力逐级降低，达到密封效果[4]。

降低航空发动机的油耗比已成为提高民用、军用航空发动机效率的关键问题。与压气机和涡轮的改进相比，密封每减少1%的泄漏，就能增加1%推力，减少0.1%油耗比[5]。此外，NASA的先进亚音速计划表明，若在几个关键位置使用先进的密封件，就能使发动机的油耗降低2.5%以上[6]。因此，降低迷宫密封的泄漏，并提升其可靠性就成为了提升发动机功耗的关键[7]。CHUPP等[8]对叶轮机械中的密封问题进行了概述，提出了其密封可靠性的关键在于泄漏系数、流量系数、换热系数、转子动力系数。WANG等[9]发现在定常状态下，密封的下游处总流量会出现一个突变。MICIO等[10]的研究表明，泄漏量随着间隙的增加而增大，并且该增大趋势并非是单调的。BOZZI等[11]设计并确定了一种非接触的密封的几何形状，从而确定了低泄漏量对于间隙的依赖性。杜发青等[12]通过正交实验研究了篦齿几何参数对于气体密封的影响，李文凯等[13]在此基础上进一步进行了数值研究，最终确定密封间隙对气体密封影响最大，其次是齿数、齿高等篦齿参数。

综上所述，密封间隙对迷宫密封的泄漏性能起着决定性的作用。但由于燃油泵运转速度极高，转子与静子之间的相对运动速度极大，使用传统的密封方法实现泵内高压燃油的密封十分困难。常规迷宫密封泄漏过大，石墨圆周密封磨损太快，这些密封方式都不能满足高速离心式燃油泵的工作需求，原因在于高速下泵转子的径向振动和变形会导致较大幅度的径向位移，如果密封件与转子之间间隙过小，就难免会加剧磨损甚至碰摩；如果间距过大，就会加大泄漏量。这一矛盾的根本问题在于，密封间隙无法自发进行调整，进而适应高速转子的运动和变形。

引入浮环密封就可以一定程度上解决密封间隙自发调整的问题。浮环密封是一种浮动式非接触密封，可用于航空发动机轴承腔等部位。与传统的篦齿密封相比，由于浮环密封可以在一定程度上适应密封间隙的改变，并进行自对心，相比迷宫密封，它可以有效降低密封间隙并减少动静碰摩[14-17]。

浮动迷宫密封在传统迷宫密封的基础上，结合了浮环密封的特点，设计并加入了一段能够依靠流体动压效应浮起的区域，通过自身的径向运动来适应转子的径向偏移，从而能够在较小的预设间隙下避免碰摩；同时它还兼顾了迷宫密封的特点，达成小泄漏和低磨损的目标。本文作者在浮动迷宫密封中加入了螺旋槽和直线槽，从而进一步提升密封环的浮动性能，并通过建立浮动迷宫密封的CFD数值分析模型，对其浮动能力、泄漏量进行仿真计算，进一步探究不同开槽方式对于浮动迷宫泄漏特性和浮起性能的影响；同时还搭建有效的验证试验平台，对数值模拟仿真结果进行验证分析。建立的浮动迷宫密封设计方法以及CFD数值分析模型，对航空动力系统中的迷宫密封性能研究有重要的参考意义。

1 数值计算模型

1.1 浮动迷宫密封结构以及原理

浮动迷宫密封一般由密封环、垫片、波形弹簧、挡圈及壳体等组成[18]，浮动迷宫密封和与之配对的主轴轴套形成主密封面，是一种非接触式密封，能适应很高的线速度，其基本结构如图1所示。工作前受重力作用密封环内壁与跑道外壁贴合，两者之间有极小的间隙，此时密封环圆心与跑道圆心的存在偏心值e，在发动机工作时，左边气体流路的压力于右边轴承腔，防止滑油泄漏。此时，通过浮动迷宫密封减少气体泄漏量，从而降低发动机的功率损耗。

图1 浮动迷宫密封结构示意

正常工作时密封环与跑道表面被刚性流体膜隔开，阻止高压侧气体向低压侧泄漏，同时密封环端面在波形弹簧及两侧气体压差的作用下紧紧贴合在壳体内侧，防止气体沿径向泄漏[19]。密封环上浮是浮动迷宫密封安全可靠工作的必要条件[20]，浮动迷宫密封只有在上浮状态下才能保证密封环与旋转跑道不会产生接触摩擦或碰撞。

为了改善迷宫密封的浮起性能，文中提出了2种优化设计结构，通过在密封跑道上开槽的方式来改变迷宫密封的气流特性，一种结构是在迷宫节流段前面增加直线槽，直线槽的尺寸为2 mm×9 mm×0.05 mm，另一种结构是在迷宫节流段前面增加螺旋槽，螺旋槽与主轴轴向呈30o夹角。直线槽与螺旋槽结构示意图如图2和图3所示。

图2 直线槽浮动迷宫密封跑道示意

图3 螺旋槽浮动迷宫密封跑道示意

1.2 浮动迷宫密封数学模型

泄漏气体为理想可压缩气体，描述气体流场的控制方程为三维的Navier-Stokes方程：

(1)

式中：t为时间;Q为守恒型变量;E、F、G为无黏通量；Ev、Fv、Gv为黏性通量；Re为雷诺数。

(2)

(3)

式中:ρ为密度;u、v、w分别为笛卡尔坐标系中沿x、y、z3个不同方向的速度分量。

黏性应力分量为

(4)

(5)

(6)

τxy=τyx=μ(uy+vx)

(7)

τxz=τzx=μ(uz+wx)

(8)

τyz=τzy=μ(vz+wy)

(9)

理想气体的状态方程为

pV=nRT

(10)

式中：p为气体压力；V为气体体积；n为物质的量；R为理想气体常数；T为温度。

1.3 浮动迷宫密封数值计算模型

利用三维建模软件分别对密封环和轴套进行实体模型的创建，然后进行偏心安装，形成三维实体模型并抽取螺旋槽浮动迷宫密封气膜模型，气膜几何模型如图4所示。

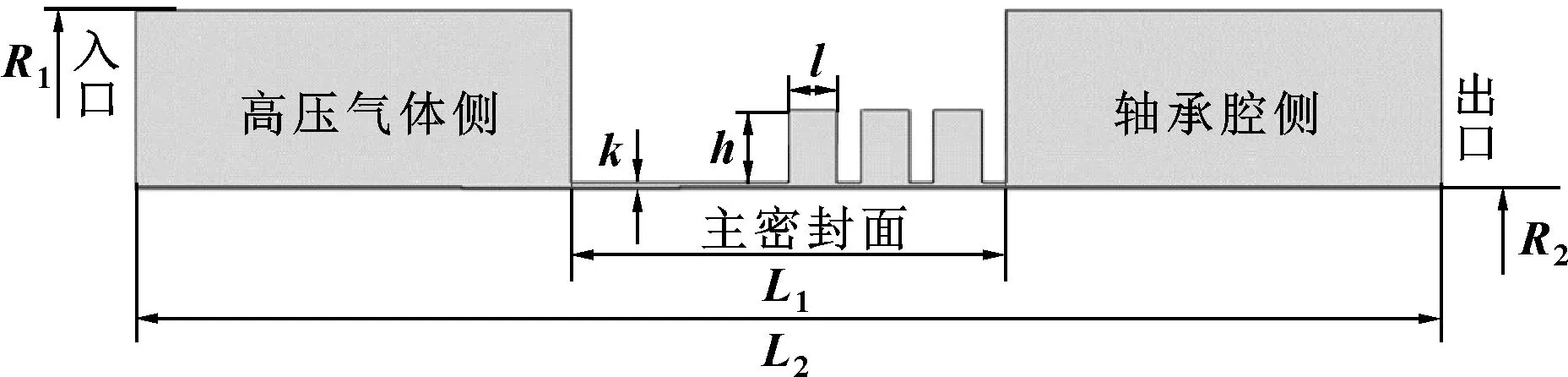
图4 数值计算几何模型

图4中几何模型具体尺寸如表1所示。

表1 浮动迷宫密封气膜模型几何尺寸 单位:mm

螺旋槽浮动迷宫密封气膜结构较为复杂，横纵尺度跨度较大，气膜整体结构存在偏心，最薄的区域只有几微米。因为气膜模型为偏心结构，不满足周期性模型划分条件，且螺旋槽为非回转结构，因此采用六面体网格方法进行划分。

工质设置为空气(理想气体)，采用标准k-ε湍流模型，湍流强度5%，迭代过程采用SIMPLE(semi-implicit method for pressure-linked equation)算法。转子和静子壁面设置为绝热光滑无滑移壁面，静态工况下偏心率为5%。在密封进口设置总压，出口设置平均静压出口，其余边界设置为壁面，包括旋转壁面和静止壁面。当各方程残差值达到10-5，进出口流量相差小于0.1%时，认为计算收敛。

工况设置为浮动迷宫密封试验件上下游压差分别为0.05、0.1、0.15、0.2、0.25和0.3 MPa，主轴转速设置为200、500、1 000、1 500、2 000、2 500和3 000 r/min，计算浮动迷宫密封的泄漏量(即计算稳定后出口的流量)和浮起力。

2 浮动迷宫密封验证试验

设计的动迷宫密封试验台示意图如图5所示。试验台主要由试验台架、检测系统、控制系统组成。试验台架主要包括电机、减速器、联轴器、轴承箱、密封试验腔及其内部主轴、轴套、带螺旋槽的浮动迷宫密封试验件组成。控制系统主要是电控箱以及控制台。检测系统由一套流量计、压力计、激光传感器、扭矩测量仪、转速测量仪构成。试验时，由控制系统给定电机转速，电机经由联轴器、轴承箱带动主轴及套在主轴上的轴套旋转，然后控制系统打开外部气体压缩机，使压缩气体经由高压气体入口流入密封腔中，泄漏气体从出口流出。试验过程中，气体流量、压力等由流量计、压力表测得，转子转速、扭矩由转矩测量仪测出，浮动迷宫密封环的位移以及自对心情况由激光位移传感器测出。由于在压力恒定后，高压气体入口进气量就为通过浮动迷宫密封的泄漏量，所以此时进气量与泄漏量相等，可以通过流量计读数得到泄漏量。

图5 浮动迷宫密封试验台示意

3 结果与分析

3.1 浮动迷宫密封浮起力分析

当转速为 3 000 r/min时，压差从0.05 MPa变化到0.3 MPa时，3种密封结构浮起力随着压差变化规律如图6所示。由图6得：随着压差的不断增加浮起力也在不断地增加，浮起力在压差为0.05 MPa到0.3 MPa范围内近似为线性增长。在0.05 MPa到0.3 MPa范围内直线槽浮动迷宫密封浮起力最大提升了32.6%，螺旋槽浮动迷宫密封浮起力最大提升了40.8%。在压差小于0.175 MPa时，直线槽对浮动迷宫密封浮起力的提升作用略大于螺旋槽，当压差大于0.175 MPa时，此时轴向流螺旋槽的提升作用较为显著。由此可见，直线槽与螺旋槽对浮动迷宫密封浮起力的影响作用相差不大，但是随着压差的逐渐增加，螺旋槽对浮起力的影响相较于直线槽而言会越来越大。

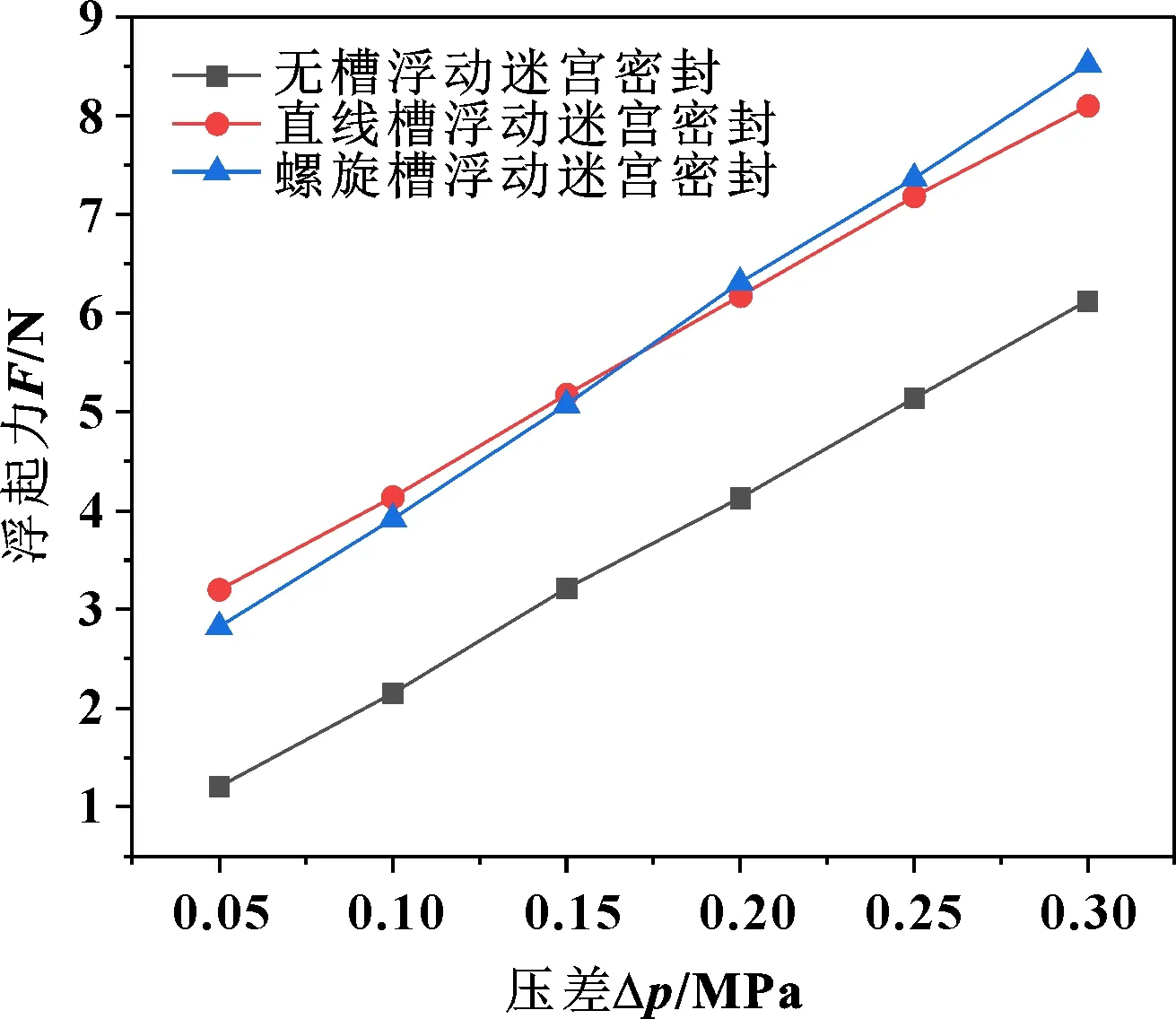
图6 转速为3 000 r/min时不同压差下3种密封结构的浮起力

当浮动迷宫密封入口出口压差为0.3 MPa，跑道转速从0变化到3 000 r/min时，浮起力随着转速变化规律如图7所示。可以看出，直线槽与螺旋槽对浮动迷宫密封浮起力的影响作用相差不大；2种开槽结构气膜模型的浮起力均大于无槽密封结构，直线槽浮动迷宫密封和螺旋槽浮动迷宫密封浮起力相对于无槽结构最大提升分别为32.45%和40.8%。这一研究结果与文献[21-22]的研究结果相似，在密封跑道的周向设置直线槽和螺旋槽，既避免了在密封环上开槽的加工难度性和减小了密封环的变形，又增加了浮动迷宫密封的浮起性能。螺旋槽随着旋转而产生的流体动压效应与气膜偏心产生的挤压效应共同提高了气膜承载力，从而支撑浮环与密封跑道分离，所以螺旋槽结构对于浮起性能的提升略优于直线槽结构。

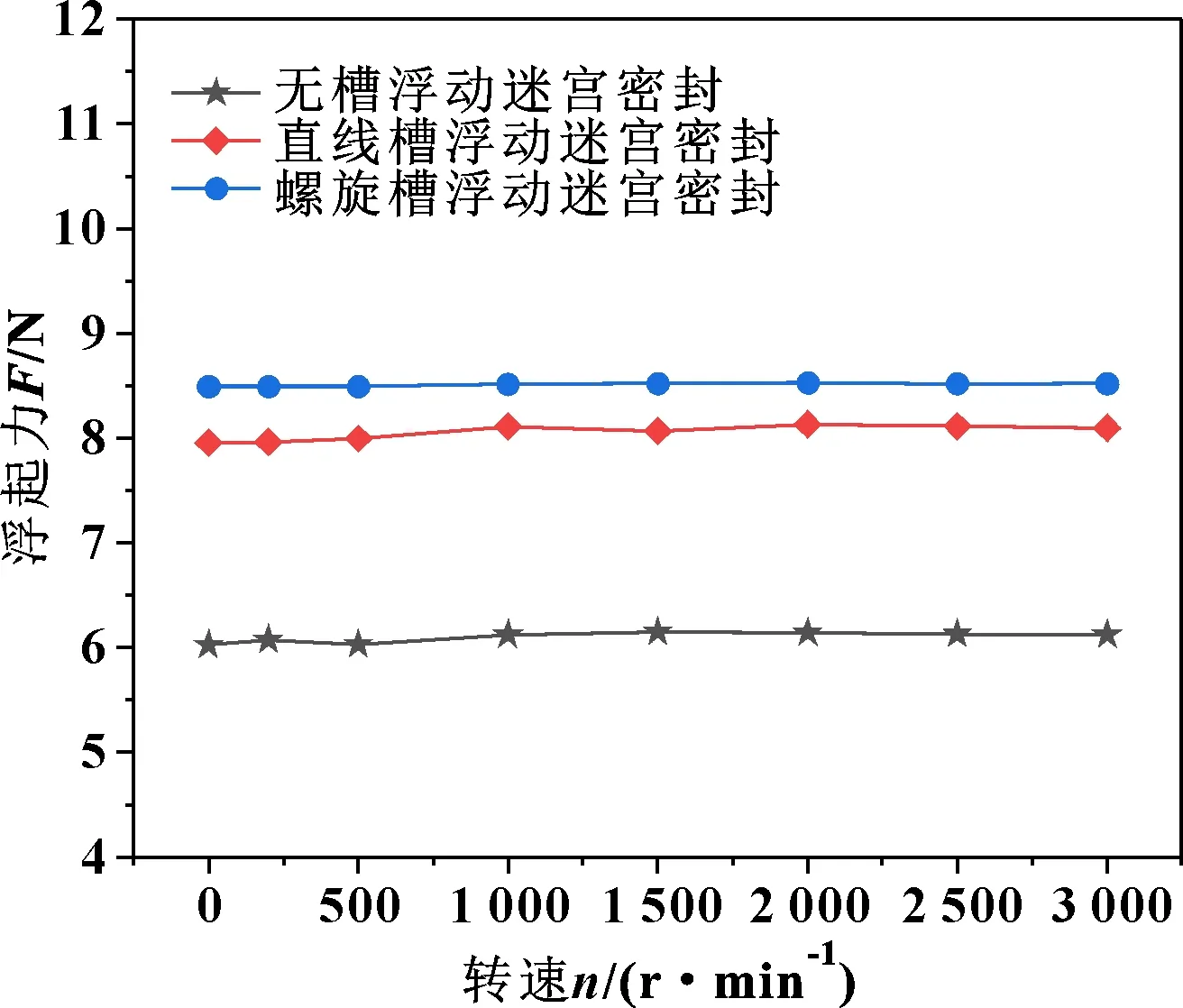
图7 压差为0.3 MPa时不同转速下3种密封结构的浮起力

3.2 浮动迷宫密封泄漏特性分析

图8所示为3种浮动迷宫密封结构沿气体流动方向的压力云图，入口压力设置为0.3 MPa,转速设置为0。可以看到，在密封环与密封跑道入口处，压力变化梯度比较大，然后再缓慢减小；改变轴套的结构，在轴套槽区部分流场压力会受到影响，直线槽与螺旋槽对压力分布的影响基本相同。

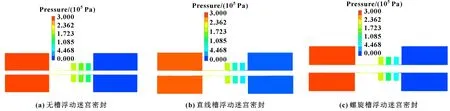
图8 3种密封结构轴向压力云图

图9所示为3种浮动迷宫密封结构槽区部分沿周向方向的压力云图，入口压力设置为0.3 MPa,转速设置为0。可以看出，无槽浮动迷宫结构在周向气膜压力均匀分布，而在轴套上切了槽以后，气膜压力在周向分布受到槽区的影响，在槽区内部会出现压力较小的区域，槽区内外出现较小的内外压差，直线槽与螺旋槽对周向压力分布影响规律基本相似。

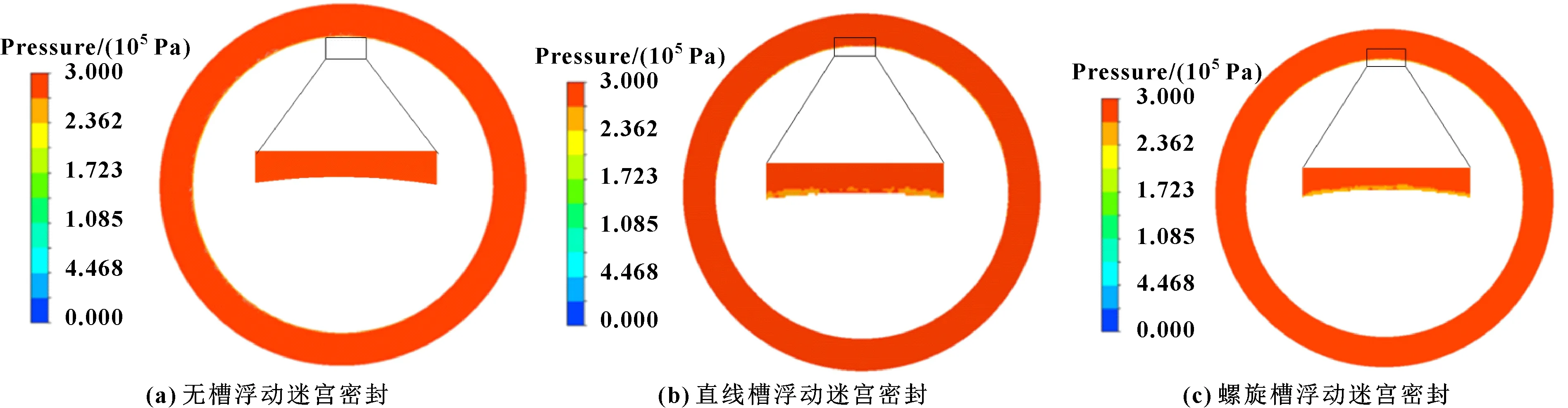
图9 3种密封结构周向压力云图

当转速为3 000 r/min时，压差从0.05 MPa变化到0.3 MPa时，3种密封结构泄漏量随着压差变化规律如图10所示。可以看出：泄漏量随着压差的增大近似呈线性地增长，在压差从0.05 MPa增长到0.3 MPa时，泄漏量变化的大致范围为12.138～43.621 m3/h。对于浮动迷宫密封，流体流动主要由跑道旋转运动产生的剪切流和进出口产生的压力梯度导致的轴向流构成。密封的泄漏主要发生在轴向和径向方向的流量，随着压差的不断增大，流速在不断地增加，轴向流量同时也在不断地增加，进而泄漏量在不断地增大。

从图10还可以看出，无槽浮动迷宫密封在不同压差下数值计算得到的泄漏量与试验结果的最大偏差为4.77%，最小偏差为1.14%。直线槽浮动迷宫密封在不同压差下数值计算得到的泄漏量与试验结果的最大偏差为4.78%，最小偏差为0.5%。螺旋槽浮动迷宫密封在不同压差下数值计算得到的泄漏量与试验结果的最大偏差为6.74%，最小偏差为2.83%。随着压差的增加，直线槽浮动迷宫密封与螺旋槽浮动迷宫密封泄漏量数值计算值最大增幅分别为16.1%和18.7%，试验值最大增幅分别为14.5%和15.1%，螺旋槽密封结构的泄漏量增幅都略大于直线槽密封结构。主要是因为螺旋槽具有和直线槽相同的轴向长度，螺旋槽结构与轴向有30°的夹角，因此螺旋槽的结构比直线槽具有更大的平均泄漏间隙。同时由于螺旋槽结构有着较好的流体动压效果[23]，所以随着压差的增加，螺旋槽浮动迷宫密封动压浮起力增加，流体间隙增加，泄漏量便有着更大幅度的增加。

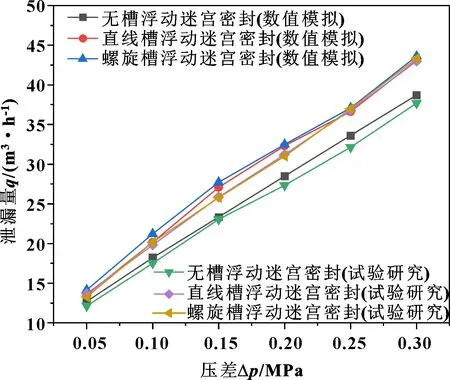
图10 3种浮动迷宫密封泄漏量随压差的变化

当浮动迷宫密封入口出口压差为0.3 MPa，跑道转速从0变化到3 000 r/min时，泄漏量随着转速变化规律如图11所示。如图11所示：泄漏量随着转速的增大只是在很小的范围内波动，转速从0增长到3 000 r/min时，无槽浮动迷宫密封结构数值计算值与试验值最大波动范围分别为0.526%与1.631%，直线槽浮动迷宫密封结构数值计算值与试验值最大波动范围分别为0.278%与2.277%，螺旋槽浮动迷宫密封结构数值计算值与试验值最大波动范围分别为0.806%与1.568%。相同转速下，直线槽与螺旋槽结构浮动迷宫密封泄漏量基本相同，但是比无槽浮动迷宫密封结构最大增加了16%，相比于压差对气膜泄漏量的影响，转速的增加对泄漏量的影响很小。随着转速的不断增加，泄漏量的增幅不断减小，逐渐趋于稳定。主要是由于浮动迷宫密封在刚启动的时候，开启力没有达到一定的值，密封系统没有稳定下来，泄漏量会波动；当转速增加到一定的值时，开启力和闭合力相等，密封系统趋于稳定，所以泄漏量也逐渐稳定下来。

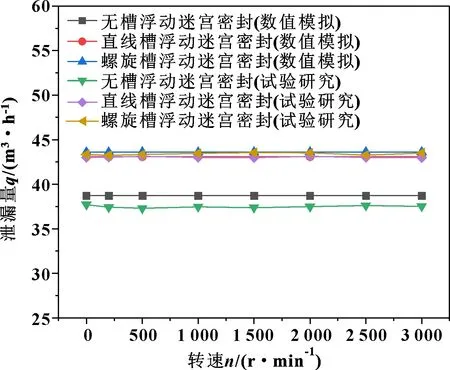
图11 3种浮动迷宫密封泄漏量随转速的变化

4 结论

(1)为了增强浮动迷宫密封的浮起性能，增强浮动迷宫密封环对于转子径向跳动的适应性，在其内部跑道设计了2种槽型的密封结构，包括直线槽浮动迷宫密封和螺旋槽迷宫密封；建立了浮动迷宫密封的流场气膜模型，计算了不同压差与不同转速工况下3种密封结构浮起力。结果表明：直线槽与螺旋槽对浮动迷宫密封浮起力影响作用相差不大，但是随着压差的逐渐增加，螺旋槽对浮起力的影响相较于直线槽而言会越来越大。

(2)为了验证数值模型计算的可靠性，进行了不同工况下的密封泄漏特性试验验证。结果表明：随着压差的增加，泄漏量随着压差的增大近似呈线性增长，直线槽浮动迷宫密封与螺旋槽浮动迷宫密封泄漏量数值计算值最大增加分别为16.1%和18.7%，试验值最大增加分别为14.5%和15.1%；随着转速的增加，3种密封结构的泄漏量变化很小，而且直线槽与螺旋槽密封结构泄漏量都大于无槽密封结构。