Python求解圆周率的方法

王德贵

圆周率π和e一样，都是常用的数学常数，且都是无理数，也称为超越数。在数学和物理课程中，经常用到π和e两个常数，也经常会想，它们是怎么算出来的？怎么被发现的呢？今天我们来学习用Python求圆周率π的近似值。

其实圆周率求解方法很多，归纳起来有大致四类方法，故称“求解圆周率四法”。我们选择其中两种来学习。

使用随机数（或更常见的伪随机数）来解决很多计算问题的方法，称为蒙特卡洛法，它是统计模拟方法。当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。主要步骤：构造或描述概率过程;实现从已知概率分布抽样;建立各种估计量。

正方形内部有一个相切的圆，它们的面积之比是π/4（图1）。

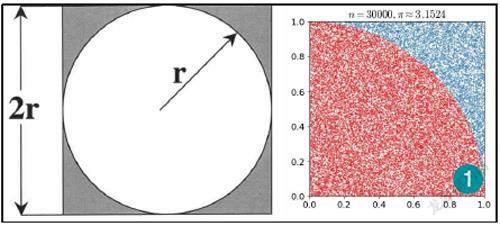
现在，在这个正方形内部，随机产生n个点，计算它们与中心点的距离，并且判断是否落在圆的内部。若这些点均匀分布，则圆周率 PI=4 * m/n， 其中m表示落到圆内投点数，n表示总的投点数。

显然投点数目越多，数值越精确，误差越小。于是我们采用循环的方法产生n个（0，1.0）区间上的随机数，即第一象限内的点，然后判断在单位圆内的个数m，求得圆周率近似值。

从前面的分析， 得出程序如下。这里用到了随机函数模块（random），利用random（）生成一个（0，1.0）之间的随机浮点数（图2）。

单位圆标准方程为x+y=1：，条件判断里，“x*x+y*y<=1”表示点（x，y）在圆上或圆内。投入1亿个点，某次运行结果为3.1515122。

利用随机数求圆周率，每次求得的近似值不一定相同。

所谓“割圆术”，是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法。

魏晋时期数学家刘徽在《九章算术注》中为“割圆术”计算圆周率建立了严密的理论和完善的算法。约480年，南北朝时期的祖冲之在此基础上算出圆周率在3.1415926和3.1415927之间，相当于精确到小数第7位，他是第一位将圆周率值计算到小数第7位的科学家。

用割圆术来求解圆周率。可以设置初始正多边形为正三角形、正方形、正六边形等等，我们用正六边形，因为此时圆半径和边长相等，计算上简便一些（图3）。

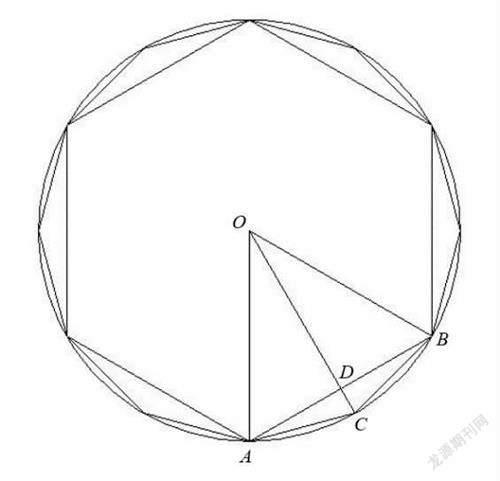
如图3所示，设圆半径为1，这样圆面积就是s=πr=π，计算出面积，即求出圆周率。基本思路就是无限的成倍分割，这样新的正多边形面积，就是在原正多边形面积基础上，每条边与圆弧之间多了一个等腰三角形，对于正六边形到正十二边形的分割中，就是多了6个的 △ABC 面积。下面进行计算。

这样依次计算下去，正多边形的面积就会越来越接近圆面积，因此，正多边形边数越多，计算越精确。

这里用到了math模块（数学基本运算库），应用之前需要导入，有两种导入方法：（1）import math;（2）from math import* 。两种导入方法的区别，是Python等级考试四级内容，大家可以注意一下，本文不做赘述。sqrt（）是开平方运算（图4）。

运行程序，输出结果如图（图5）：

误差已经很小了。当然如果边数小于6，那就按六边形算的了，所以取值要尽量的大，才会更接近圆周率的真值。

Python默认有效数字为17位，那么如何得到更精确的位数呢？

我们可以利用decimal模块求解18-100位精度的有效数字，默认值为28位。decimal意思为十进制，提供了十进制浮点运算支持，主要是用来处理要求特别精确的小数。decimal所表示的数是完全精确的，而float浮点数不能使用decimal，因为float浮点数本身就不精确。

getcontext（）.prec = 50，即设置精度为50位（图6）。结果如图7。

从输出可以看到第一行是28位有效数字，这是默认值。第三行是50位有效数字。第二和第四行，与设置精度无关，因为它们是浮点数转换过来的，不准确。要想精度提高，必须将数值转换为字符再输出。

下面是割圆术基础上，设定有效数字位数，来求近似值的程序（图8）。

運行结果（图9）：

如果超过100位呢？那么后面就都用0补充了。更多位也不会有区别了（图10）。

想要更精确的结果，必须设定小数点后位数，可以先放大多少倍，最后计算结束时再舍去多少位，以保证精度，这个过程稍难，程序如图11。

运行结果可以看到，可以精确到小数点1000位（图12）。

大家可以自己验证，程序可以求出任意位数的小数。你注意到了吗？程序是把计算结果，转换为字符串后处理输出的，这是因为输出整数时，会自动转换为科学记数法，不会显示多于17位的有效数字。

SymPy模块可以进行符号计算，可以定义符号变量，进行代数运算，以及微分运算、积分运算等。利用evalf（）函数传递数据。比如要输出1000位有效数字，则程序为（图13）：

结果如图14：

从前面的分析和测试中，我们看到求解圆周率的方法很多，精度也不尽相同，一般来说Python默认的17位有效数字已经足够了，如果需要高精度的结果，需要使用相应的方法。

通过圆周率的计算，我们也更深刻了解了圆周率的发展史。电子计算机的出现，把计算精度提高到了惊人的数量级。现在圆周率最高位数已计算到31.4万亿位，准确地说是31415926535897位，是2019年工程师爱玛在谷歌云平台的帮助下完成的。比2016年的纪录又增加数万亿位。

其实π精度的追求更多的是人类对极限的追求，毕竟十位小数的π就足以使地球周界准确到一英寸以内，三十位小数的π便能使整个可见宇宙的四周准确到连最强大的显微镜都不能分辨的一个量。

如果你对此感兴趣，可以继续深入研究，求出更多位数，刷新圆周率计算史上的纪录，成为一名数学家！