改进的无约束优化3D-DV-Hop定位算法*

张 晶，李 煜

(1.昆明理工大学信息工程与自动化学院，云南 昆明 650500；2.云南枭润科技服务有限公司，云南 昆明 650500；3.昆明理工大学云南省人工智能重点实验室，云南 昆明 650500；4.昆明理工大学云南省计算机技术应用重点实验室，云南 昆明 650500)

1 引言

无线传感器网络WSNs(Wireless Sensor Networks)是由许多具有感知和通信功能的传感器节点部署在某个区域中组成的感知网络[1]，随着科学技术的发展和人民生活水平的日益提高，传感器的身影已经随处可见。比如，畜牧业中羊群的检测与跟踪，森林火灾的检测，甚至战争中敌军的行动检测等等。传感器网络感知的信息很重要，可是在更多时候，人们更需要信息的发生位置[2]。为此，国内外的一批学者对无线传感器网络的定位算法进行了深入研究。由于实际部署的地点往往是三维空间而少有二维平面，因此本文主要研究传感器网络的三维定位问题。

目前根据是否需要实际测量节点之间的距离，无线传感器网络的定位算法分有2种[3]：一种是需要给传感器附加额外装置来获取节点之间的间距(称为测距算法)。这种算法更精准，但是由于需要添加额外的硬件设备也使得这种算法的部署对节点成本的要求较高[4]，不适合大型区域的监测。另一种是不需要添加任何其他硬件设备对节点间间距进行测量，只需要依靠网络拓扑结构即可完成定位的非测距算法。这种算法定位精度低，但由于其相对测距算法而言节点造价低，适合于大型无线传感器网络的监测，成为近些年研究的热点。本文要探讨的就是非测距算法中的典型算法——DV-Hop三维定位算法。

DV-Hop三维定位算法可以从3个方面进行优化：跳数优化、平均跳距优化以及对未知节点的估计。文献[5]提出新的平均跳距计算方法，对定位精度有一定优化，但是计算时采用的跳数未经优化，本身就会引入误差，其次最后采用传统极大似然估计法对节点进行定位，不能将定位误差最小化。文献[6]对平均跳距进行优化，同时升级辅助锚节点以提高定位覆盖率，但是使用遗传算法计算节点位置，过多的迭代次数增加了节点计算开销。文献[7]的算法在第2阶段使用蛙跳算法改进跳距误差，并在第3阶段使用混合遗传-粒子群算法，提高了定位精度，但大量的仿生计算也极大增加了传感器节点的功耗和定位所需的时长，对于节点能量有限的传感器来说是不合适的。文献[8]使用2种灰狼算法对平均跳距进行优化，对精度有一定提升效果，但是未对跳数进行优化，且使用的最小二乘法没有考虑到权值误差最小化问题。

综上所述，现有大多数三维定位算法都是采用仿生算法或者机器学习[9]的算法进行优化，虽然取得了一定的效果，但是对于能量有限的传感器而言，计算任务过于繁重。然而最小二乘法[10]的整体误差最小化思想又无法对未知节点进行精确求解。本文针对传统DV-Hop三维定位算法定位精度低，且传感器节点能量有限不适合进行大量计算和通信的特点，对DV-Hop算法进行改进。针对DV-Hop三维定位算法的定位方式，本文从3个方面对其进行优化：(1)采用二通信半径(分别为R和0.5R)优化跳数值；(2)采用平方代价函数计算跳距，并对其进行加权优化；(3)使用Lagrangian乘子法求解未知节点方程组，将最小二乘的整体误差最小化转换加权误差最小化，使用加权误差最小化的思想来对未知节点进行定位计算。最后通过4种算法进行实验，结果表明，本文算法在不需要进行大量计算的基础上，能够大大提高节点定位精度，降低误差率。

2 传统DV-Hop三维定位算法和误差原因探讨

2.1 传统DV-Hop三维定位算法

传统DV-Hop三维定位算法包括3个步骤，分别是：

Step1确定最小跳数值。在开始组网过程中，每个锚节点使用通信半径R将包含自身编号id、所处GPS定位信息和跳数值为0的数据包发送给邻居节点，并且每经过一次邻居节点的转发就对跳数值增加1。当邻居节点(可能是未知的节点或锚节点)接收到该类数据包之后，分2种情况处理：若自身已经接收到该id编号的数据包，则对比路由表中具有相同id编号的数据包和接收到的数据包的跳数值大小，如果接收到的数据包中的跳数值比存储的小，则用接收到的跳数值替换已存储的跳数值；若接收到数据包中的跳数值大于存储在路由表具有相同id编号的跳数值，则舍弃本次接收到的数据包。如此重复，便能得到对于各锚节点而言的最小跳数值。

Step2计算锚节点的平均跳距值和未知节点与各锚节点的距离。通过Step 1获取到与各锚节点之间的最小跳数值之后，在传统算法中，锚节点的平均跳距值的计算如式(1)所示：

HopSizei=

(1)

其中,j=1,2,…,m且i≠j，m为锚节点数量,(xi,yi,zi)和(xj,yj,zj)是由GPS定位出的锚节点i和锚节点j的三维位置信息，hij为锚节点i距锚节点j的最小跳数(由Step 1得出)。

计算出所有HopSizei后，每个锚节点使用通信半径R对其计算出的HopSizei进行广播,未知节点p只存储第1次接收到的平均跳距值。当未知节点p接收到锚节点i传来的HopSizei时，使用式(2)计算其与各锚节点的估计距离：

dp,j=HopSizei×hpj

(2)

其中，dp,j表示未知节点p与锚节点j在三维空间中的估计距离，j=1,2,…,m。

Step3未知节点坐标估计。本文令未知节点p的三维位置信息为(x,y,z)，由GPS定位的第i个锚节点的三维位置信息为(xi,yi,zi)，其中i=1,2,…,m，根据Step 2计算出的p与各锚节点的估计距离d1,d2,…,dm，可以利用极大似然估计法列出如式(3)所示的方程组：

(3)

式(3)的矩阵形式为AX=B,其中，

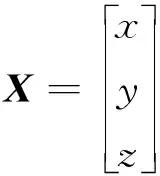
B=

使用最小二乘法,可以解得：

X=(ATA)-1ATB

(4)

2.2 算法误差产生原因

在传统DV-Hop三维定位算法中，对跳数的估计是不精确的，如图1所示。

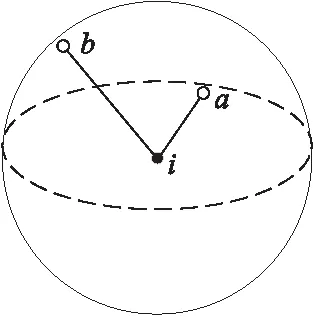
Figure 1 Schematic diagram of hop error图1 跳数误差示意图

从图1中可以看出，未知节点a与锚节点i的距离大约为0.5R，未知节点b与锚节点i的距离为R，但是由于未知节点a和b在传统DV-Hop算法中的跳数值均为1，导致节点a估算的距离与实际的距离0.5R差别很大，引入了接近一倍的误差，降低了定位精度。定位误差产生过程如图2所示。

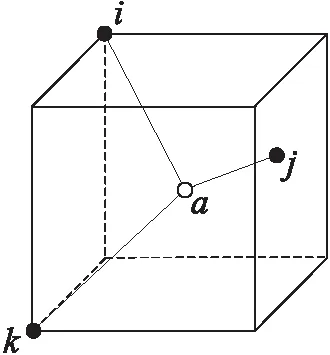
Figure 2 Generation process of positioning error图2 定位误差产生过程

在图2中，锚节点i,k与未知节点a的距离为R，锚节点j与未知节点a的距离略小于0.5R，此时传统DV-Hop三维定位算法依然将其跳数值处理为1，其与i、k和j的距离本应为1*HopSize,1*HopSize和0.5*HopSize，却由于跳数值为1变为1*HopSize,1*HopSize和1*HopSize,由此造成了定位误差。

其次，传统DV-Hop三维定位算法处理每个锚节点的平均跳距时，采用的代价函数如式(5)所示：

(5)

最后，传统DV-Hop三维定位算法采用极大似然估计[11]的思想列出的方程组并没有考虑误差的权值，且使用最小二乘法对方程进行求解，然而最小二乘法在矩阵接近奇异时的求解也十分不理想，因此造成了2方面误差的产生。

3 改进的DV-Hop三维定位算法

由于传统DV-Hop三维定位算法的一系列缺点[12]，本文结合无线传感器网络的特点，从3个方面分别进行改进。

3.1 最小跳数值的修正

传统DV-Hop三维定位算法在获取最小跳数值时，只采用了一个通信半径[13]，这样做的缺点有：若通信半径过大，则会造成最小跳数值极不准确；若通信半径过小，则会造成网络连通性很差，甚至出现盲节点。为此本文提出二通信半径的思想：

在执行Step 1之前，锚节点使用通信半径的一半(0.5R)传播数据包，相邻节点接收到数据包存储在数据表中，考虑到传感器节点特点，相邻节点并不转发数据包，随后，锚节点使用通信半径R对数据包(同Step1)进行洪泛，以此获得修正的跳数值，从而使得节点之间的最小跳数值更准确。

3.2 平均跳距的改进

3.2.1 采用平方代价函数计算HopSize

在传统DV-Hop三维定位算法中，采用代价函数f1的计算方式不理想，所以本文采用平方代价函数f2计算平均跳距值，如式(6)所示:

(6)

对HopSizei求偏导，并令其值为0，即:

(7)

则可以求解出平均跳距值HopSizei如式(8)所示:

(8)

3.2.2 平均跳距的加权

DV-Hop的定位实质上与节点的拓扑有着密切的关系，当未知节点与多个锚节点之间的距离和跳数均相差不大时，单单依靠一个锚节点的平均跳距就会产生相当大的误差，但是若采用全部锚节点进行加权，则会增加不必要的计算量,因此应当有选择性地选择锚节点的个数。为此，本文采用对距未知节点最近的3个锚节点引入权值的思想，仅对距离未知节点最近的3个锚节点引入权值1，其余锚节点权值均为0，即只使用3个锚节点的平均跳距信息。由于这3个锚节点与未知节点的距离是有区别的，越靠近未知节点的锚节点越能反映出未知节点周围的拓扑情况，使用该锚节点的平均跳距的权重也应当越大。本文使用Wi来表示锚节点i的平均跳距对于未知节点的权重比例，如式(9)所示：

(9)

其中，i、j和k分别是与未知节点距离最近的3个锚节点，Ni、Nj和Nk分别是未知节点与锚节点i、j和k经过最小跳数修正后得出的跳数值。

在本文中，未知节点p平均跳距采用式(10)进行计算：

(10)

3.3 无约束的Lagrangian乘子法

3.3.1 构造无约束方程组

传统DV-Hop三维定位算法，几乎都是使用蛙跳算法、差分进化算法和遗传算法等一类仿生算法来求解式(3)，不可否认这些算法都相当优秀，但是过多的迭代次数和庞大的计算量加剧了传感器网络的能量消耗。本文使用无约束的Lagrangian乘子法对未知节点进行求解。

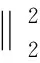
(11)

用前m-1个方程依次减去最后一个方程并展开得到式(12)：

(12)

(13)

令：

ai=2(xm-xi)

bi=2(ym-yi)

ci=2(zm-zi)

αi=-2di

β=2dm

则式(13)可以写成如式(14)所示形式：

(14)

式(14)的矩阵形式为CY=D，其中,

Y=[x,y,z,e1,e2,…,em]T

D=[D1,D2,D3,…,Dm-1]T

经过上述一系列步骤，求解问题转换为式(15)所示的约束问题:

s.t.CY=D

(15)

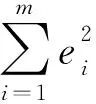
为体现出误差的权值性，本文在此引入权值矩阵Q对误差项进行加权，从而将问题转化为权值误差最小化问题：

于是约束问题转换为式(16)所示形式：

mineTQe

s.t.CY=D

(16)

使用Lagrangian乘子法将式(16)的约束问题转换成无约束问题，如式(17)所示：

(17)

其中，λ为Lagrangia乘子，λ>0且为常数。

3.3.2 无约束方程的求解

首先令f对矩阵Y求梯度矩阵为：

(18)

f对矩阵Y的Hessian矩阵为：

H[f]=2(Z+λCTC)

(19)

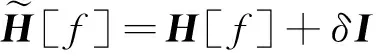
H[f]=2(Z+λCTC+δI)

(20)

其中，δ为扰动因子且δ>0，I为m+3阶单位矩阵。

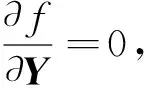
Y=(Z+λCTC)-1λCTD

(21)

由于H[f]为正定矩阵，所以Y=(Z+λCTC+δI)-1λCTD，至此,可以解得未知节点的坐标 。

4 仿真结果及分析

4.1 仿真环境及评价指标

为验证本文算法与传统算法、改进算法1、改进算法2的定位精度，在Matlab 2016a中进行仿真实验。其中改进算法1采用本文提出的跳数、跳距优化及最小二乘法的策略；改进算法2采用本文提出的跳数、跳距优化及粒子群算法的策略。实验场景为边长均为100 m的山区地形环境，并于其中随机投放未知节点和锚节点[14]，如图3所示。

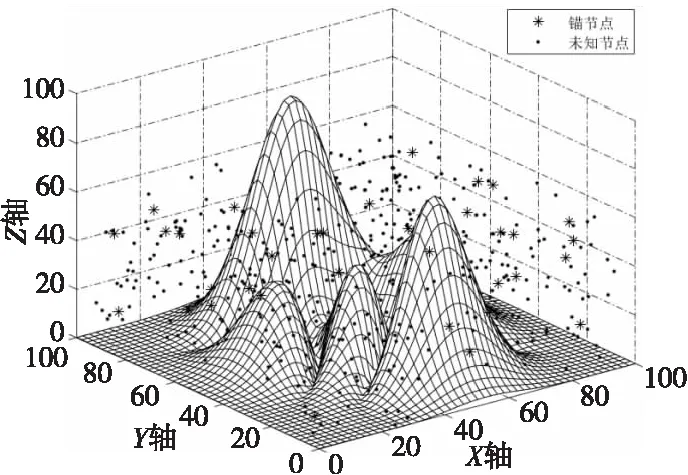
Figure 3 Node 3D distribution map图3 节点三维分布图

本文使用式(22)所示的未知节点平均定位误差作为评价算法优劣的标准[15]：

Avg_error=

(22)

其中,(xi,yi,zi)为未知节点的真实三维坐标，(x′i,y′i,z′i)为通过算法求出的未知节点的三维坐标，n为实验中未知节点的个数。

4.2 仿真结果分析

本文从锚节点数、通信半径和节点总数3个方面来对4种算法进行分析讨论。

4.2.1 锚节点数与平均定位误差分析

在边长均为100 m的山区地形环境随机投放200个节点，且实验采用的通信半径均设置为40 m,观察当锚节点比例变化时，对4种算法定位误差的影响，其中锚节点比例分别取0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5。实验结果为各类算法运行100次的均值，并绘制变化趋势图，如图4所示。

Figure 4 Trend of anchor node proportion and average positioning error图4 锚节点比例与平均定位误差的关系变化趋势图

从图4中可以看出，4种算法的平均定位误差均随着锚节点比例的增加而下降，且改进算法2的平均定位误差略低于本文算法的。在整个实验过程中，传统算法、改进算法1和改进算法2的平均定位误差分别为0.318 1,0.207 6和0.113 0,本文算法的平均定位误差为0.118 6。具体变化情况如表1所示。

Table 1 Average positioning errors under different anchor node proportion

从表1中可以得出，在锚节点比例为0.1时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.203 2,0.080 2,-0.003 5；在锚节点比例为0.3时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.197 5,0.091 5,-0.007 8；在锚节点比例为0.5时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.200 8,0.095 1,0.000 7。由此可知本文算法不论在何种锚节点比例情况下，相对于传统算法均能将平均定位误差降低0.20左右，相对于改进算法1均能将误差降低0.09左右，相对于改进算法2而言，本文算法仍具有与其相当的精度。

4.2.2 通信半径与平均定位误差分析

在边长均为100 m的山区地形环境随机投放200个节点，且实验采用的锚节点比例均设置为0.25，观察当通信半径变化时，4种算法的平均定位误差变化趋势，其中，通信半径分别为40,45,50,55,60,65,70，实验结果为各类算法运行100次的均值，并绘制变化趋势图，如图5所示。

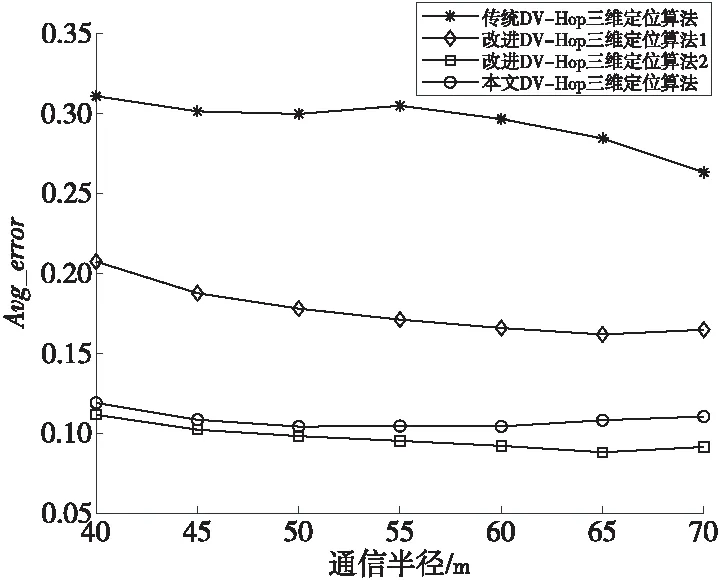
Figure 5 Trend of communication radius and average positioning error图5 通信半径与平均定位误差的关系变化趋势图

从图5中可以看出，传统算法与改进算法1的平均定位误差均随着通信半径的增加而降低，改进算法2与本文算法的平均定位误差虽随通信半径变化不大，但均处于较高精度水平。整个实验过程中，传统算法、改进算法1和改进算法2的平均定位误差分别为0.294 2,0.176 5,0.096 9,本文算法的平均定位误差为0.108 3。具体变化情况如表2所示。

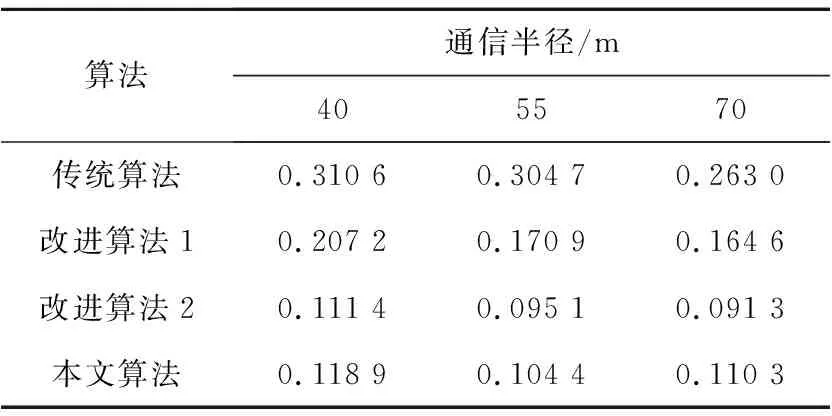
Table 2 Average positioning error under different transmission radius

从表2中可以得出，在通信半径为40 m时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.191 7,0.088 3,-0.007 5；在通信半径为55 m时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.200 3,0.066 5,-0.009 3；在通信半径为70 m时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.152 7,0.054 3,-0.01 9,其中本文算法与改进算法2在通信半径为65 m时误差相差最大仅为0.02，故从本文算法与改进算法2在整个实验中的平均定位误差均值与其之间的最大误差差值来看，这种差值仍是可接受的良性水平。

4.2.3 节点总数与平均定位误差分析

在边长均为100 m的山区地形环境内，设置锚节点比例恒定为0.4，参与实验节点通信半径均设置成50 m，观察节点总数变化，对4种算法平均定位定位误差的影响，其中，节点总数分别为100,150,200,250,300,350,400,450,500。实验结果为各类算法运行100次的均值，并绘制变化趋势图，如图6所示。

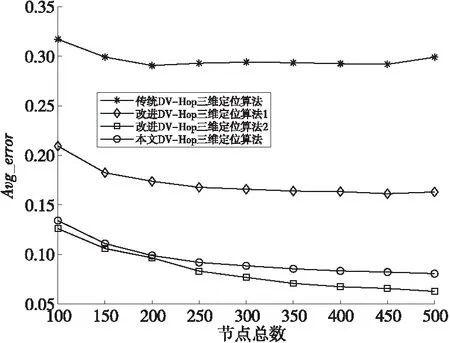
Figure 6 Trend of total number of nodes and average average positioning error图6 节点总数与平均定位误差的关系变化趋势图

从图6中可以看出，在节点总数大于250时，改进算法2与本文算法定位精度差距变大。在整个实验过程中，传统算法、改进算法1和改进算法2的平均定位误差分别为0.296 7,0.172 4,0.084 0，本文算法的平均定位误差为0.095 2。具体变化情况如表3所示。

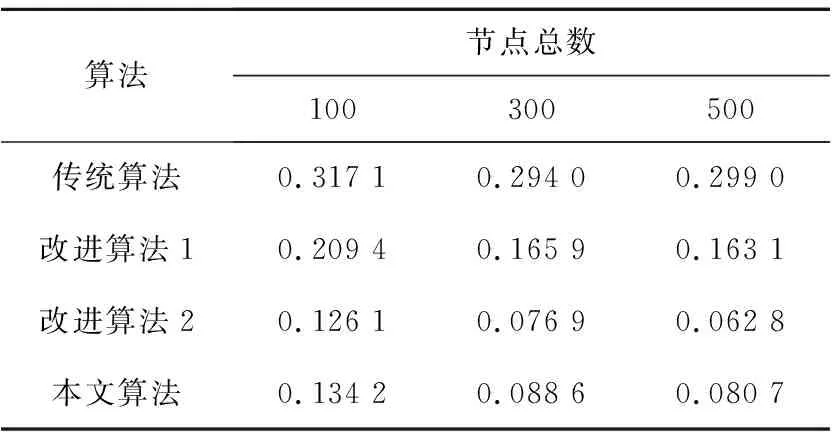
Table 3 Average positioning errors under different total number of nodes

从表3中可以得出，在节点总数为100时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.182 9,0.075 2,-0.008 1；在节点总数为300时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.205 4,0.077 3,-0.011 7；在节点总数为500时，本文算法相对传统算法、改进算法1和改进算法2的平均定位误差分别降低了0.218 3,0.082 4,-0.017 9,其中改进算法2与本文算法在整个实验过程中的平均定位误差差值为0.002 4和0.017 9，节点总数为200时平均定位误差差值最小，节点总数为500时平均定位误差差值最大。不论是平均定位误差还是最大定位误差差值，本文算法在不进行大量计算的情况下与使用仿生算法的改进算法2之间的误差差值都是比较小的。

4.3 算法计算复杂度与计算时间分析

算法的计算复杂度与该区域未知节点数相关，令频度函数为T(η)=(1-δ)η，其中，η为节点总数,δ为锚节点比例，令T(η)的各未知项均为υ，可得T(υ)=υ2，故可知传统算法与改进算法1及本文算法的计算复杂度均为O(υ2)。改进算法2的频度函数为T(η)=(1-δ)η·MAXG·NP，其中,MAXG为最大迭代次数，NP为种群数量，令T(η)的各未知项均为υ，可得T(υ)=υ4，因此改进算法2的计算复杂度为O(υ4)，远高于本文算法的计算复杂度。

在一个1.8 GHz Intel Core i7 CPU和8 GB RAM的系统上测试各算法的运行时间，其中锚节点比例为0.3，通信半径为50 m，改进算法2的MAXG为100，NP为100，时间结果取算法运行100次的均值，如表4所示。

Table 4 Comparison of algorithm average running time under different conditions

不论从计算复杂度还是计算时间来看，改进算法2的计算代价比本文算法都要高，而本文算法与改进算法2之间的最大定位误差差值却不到0.02，本文算法在不使用大量迭代运算的前提下，对精度的提升是十分明显的，也是具有实际应用意义的。

5 结束语

本文指出了传统DV-Hop三维定位算法在跳数计算、平均跳距计算和最小二乘法的不足3个方面的缺陷，并有针对性地提出了改进方法：采用二通信半径使得跳数计数更为准确；采用平方代价函数的思想使跳距误差更小，并针对未知节点与多个锚节点相邻的情况，提出加权跳距的方案；使用无约束优化并对误差加权，使得加权误差最小化。最后通过实验表明，本文算法在不进行大量计算的前提下能够大大提升定位精度，具有较好的应用前景。