考虑倾角影响的扩大头锚杆极限抗拔力

2022-01-24江建洪曾庆义

哈尔滨工业大学学报 2022年2期

江建洪，曾庆义，马健

(1.苏州大学轨道交通学院，江苏苏州 215131；2.深圳钜联锚杆技术有限公司，广东深圳 518034；3.上海勘察设计研究院(集团)有限公司，上海 200093)

扩大头锚杆因其抗拔承载力高、适应性广和安全经济等优点日益得到广泛应用[1]。但目前关于扩大头锚杆的力学机制和抗拔力计算理论仍在不断发展中[2-15]。现行的《建筑基坑支护技术规程》[16]对锚杆极限抗拔力仅考虑了锚固体与所在土层之间的摩阻强度。在关于摩阻强度的经验表格中，对扩孔工艺施工的锚杆建议在表中数值基础上适当提高，这种做法经验性较强，没有考虑扩大头锚杆端部正压力所提供的抗拔力。郭文龙等[2]采用有限差分法研究了竖向扩大头锚杆的抗拔力及相关影响因素。郭钢等[3]通过室内试验研究了竖向扩大头锚杆的各阶段破坏及其规律。陈帅等[4]结合极限分析法和有限差分法研究了抗浮锚杆的抗拔力及相关影响因素。李粮纲等[5]结合弹性理论和现场试验对竖向扩大头锚杆的最大抗拔力计算公式及相关影响因素进行了探讨。以上研究均集中于竖向扩大头锚杆的抗拔力。刘波等[6]通过现场试验对扩大头锚索在饱和粉细砂层中的受力特性进行了研究，考虑了锚杆倾角的影响。国外研究大都集中在无黏性土中完全竖直或水平的板式锚杆的极限抗拔力[7-8]，对倾斜的情况也有一定的研究[9-13]。Frydman等[9]针对埋置于砂土中的板式锚杆，根据试验结果提出了锚杆倾角对板前土压力影响的经验表达式，但该公式仅仅是曲线拟合表达式，不包含砂土性质的相关物理量。Murry等[10]采用极限分析方法得到了无黏性土中板式锚杆倾斜情况下的极限抗拔力，并与已有相关试验结果进行了对比。Hanna等[11]根据试验现象提出破坏面假设，推导了砂土中板式锚杆倾斜情况下的极限抗拔力。Bhattacharya等[12]结合极限分析下限法和有限元方法考察了砂土中不同倾角下板式锚杆的极限抗拔力。Yu等[13]采用块体理论分析了砂土中不同倾角下板式锚杆的极限抗拔力。以上板式锚杆抗拔力的研究可供扩大头锚杆的端压力研究借鉴，但仅限于无黏性土的情况，对其他土体的适用性有待考察。Xanthakos[14]针对无黏性土和黏性土地层分别给出了考虑扩大头端压力的极限抗拔力表达式，但相关的承载系数经验性较强，没有考虑锚杆倾角的影响，且应用范围较小。曾庆义等[15]根据扩大头锚杆的受力过程，提出了其极限端压力和极限抗拔力的计算方法，并为现行的《高压喷射扩大头锚杆技术规程》[17]和公司规程[18]所采用。曾庆义等[15]对扩大头锚杆端压力的表达式局限于锚杆完全水平或完全竖直的情况，而规程[17-18]对于扩大头锚杆倾斜的情况，近似采用锚杆完全水平时的端压力。

应该认识到，扩大头锚杆为了提高其抗拔承载力往往需要避开软弱土层，而将扩大头选择设置在工程性质较好的土层中，这就使得扩大头锚杆往往具有一定的倾角。因此，锚杆倾角对扩大头锚杆的极限端压力及极限抗拔力的影响值得深入研究。本研究在原有工作基础[15]上，提出考虑倾角影响的扩大头锚杆极限抗拔力计算方法。

1 扩大头锚杆抗拔力计算公式

1.1 力学模型

扩大头锚杆的破坏形式可以是杆体破坏、扩大头段注浆体与杆体握裹力破坏或扩大头端周土体破坏。扩大头锚杆的极限抗拔力应是抵抗这3种破坏的抗拔力最小值。前两种破坏形式可以通过选择合理的结构参数来避免。在第3种破坏形式中，土体随锚杆位移表现出不同阶段的力学反应，包括静止土压力阶段、过渡阶段和塑性区压密-扩张阶段[15]。本研究主要讨论基于第3种破坏形式的扩大头锚杆抗拔力，相应的力学模型见图1。

图1 扩大头锚杆力学模型Fig.1 Mechanical model for end-expanded ground anchor

如图1所示，扩大头锚杆的抗拔力T由3部分组成，包括普通锚固段锚固体侧壁与土体摩阻力所提供的抗拔力T1、扩大头侧壁与土体摩阻力所提供的抗拔力T2和土体对扩大头端部正压力所提供的抗拔力T3，具体如下[15,17]：

T=T1+T2+T3

(1)

T1=πD1L1τf

(2)

T2=πD2L2τfd

(3)

(4)

式中：D1和D2分别为锚杆钻孔直径和扩大头直径，L1和L2分别为非扩大头锚固段计算长度和扩大头长度，τf为非扩大头锚固段地层与锚固体侧壁之间的摩阻强度，τfd为扩大头侧壁与地层之间的摩阻强度。L1、τf和τfd的确定可参考现行的《高压喷射扩大头锚杆技术规程》[17]。在某些情况下，取L1=0而使得T1=0，这将在第2节详细说明[17]。pD为土体作用于扩大头端面上的正压力强度(简称端压力),pD与扩大头埋深、扩大头前端土体性质及锚杆的工作状态有关。不同工况下pD确定后，锚杆抗拔力T可由式(1)～(4)确定。

1.2 基本假定

为确定不同工况下pD，采用曾庆义等[15]工作的4条假定[15]：1)扩大头埋深足够深；2)忽略扩大头前端锚杆杆体对土体应力状态的影响；3)土体单元在某一方向上的压力增量σT，将在与该方向垂直的其他方向产生侧压力增量ξσT，其中,ξ为侧压力系数，并假定ξ大于0且小于1；4)土体处于极限平衡状态时，符合莫尔-库伦强度理论。

曾庆义等[15]对侧压力系数ξ进行了深入讨论，并推荐ξ的经验范围为

ξ=(0.5～0.95)Ka

(5)

式中：Ka为扩大头前端土体的朗肯主动土压力系数，Ka=tan2(45°-φ/2)；φ为扩大头前端土体的内摩擦角。

曾庆义等[15]同时假设锚杆为完全水平或完全竖直[15]。此处取消该假设，考察与水平向呈任意倾角下锚杆的极限抗拔力。如图1，锚杆与水平向夹角为α，与竖直向夹角为β，二者满足α+β=90°。为叙述方便，以下将夹角α简称为锚杆倾角，取值为[0°，90°]。

1.3 扩大头锚杆极限抗拔力的计算公式

一般情况下，土体的静止土压力系数K0<1。如对于正常固结黏土或松砂，常用Jaky公式[19]：K0=1-sinφ，其中,φ为土体的内摩擦角。而曾庆义等[15]在其锚杆抗拔力公式中K0的建议表达式为

K0=1-sin(1.3φ)

(6a)

但对于某些超固结土，其K0可能大于1。比如Mesri等[20]在文中图19给出了各种砂土随超固结比增大的情况，其K0可达2.0左右；在文中图27给出了一种超固结黏土的竖向应力与水平应力关系，其K0为1.63。Das[21]给出了超固结土的静止土压力系数K0,OC与其对应的正常固结土静止土压力系数K0,NC之间的经验关系，即

(6b)

式中ROC为土体的超固结比(OverConsolidation Ratio)。

K0的大小影响土体单元初始大小主应力的确定，因此，此处将区别K0不大于1与大于1这两种情况对扩大头锚杆的抗拔力分别进行讨论。认识到当超固结比较大、K0>1时，土质往往较好，有时采用非扩大头的常规锚杆也能满足工程要求。为保持理论的完整性，下文还是将这两种情况分别进行分析。

1.3.1 静止土压力系数不大于1的情况

在图1中锚杆扩大头前端取一土体单元进行分析，其受力变化情况如图2，相应的应力莫尔圆如图3。为叙述方便，与水平方向呈α角的面称为α面，而另一个与水平方向呈β角的面称为β面。初始应力状态如图2最左侧的单元受力情况。由于锚杆拉力在α方向产生应力增量σT,β面将产生正应力增量σT，而与β面相垂直的其他面产生正应力增量ξσT，最终的应力状态如图2最右侧的单元受力情况。与α面和β面均垂直的另一个面是一个主应力面，其应力变化为在初始地应力的基础上增加正应力增量ξσT。

图2 土体单元受力变化Fig.2 Evolution of stress state for a soil element

图3 土体单元受力变化的莫尔圆(K0≤1)Fig.3 Mohr′s circles for evolution of stress state for a soil element (K0≤1)

在图3莫尔圆中，A点和A′点分别代表α面的初始应力状态和最终应力状态，C点和C′点分别代表β面的初始应力状态和最终应力状态，B点代表与α面和β面均垂直的第3个面的初始应力状态。假设土体单元的初始竖向主应力为σz,0=γh，其中,h为扩大头前端中点到地面的埋深，γ为扩大头上覆土层的加权平均重度。B点的应力状态为(K0σz,0,0)。由于K0≤1，K0σz,0为小主应力，B为图3左侧初始莫尔圆的小主应力点。第3个面产生应力增量ξσT后，应力状态用B′点表示，其坐标为(K0σz,0+ξσT,0)。假设A′点和C′点组成的莫尔圆交正应力坐标轴于S点和Q点。由于应力增量σT较大，右侧Q点的正应力为最终状态的大主应力σ1，而B′点的正应力为最终状态的小主应力σ3，即σ3=K0σz,0+ξσT。以B′Q为直径的莫尔圆是包含最大和最小主应力的应力圆。根据莫尔-库伦强度理论，σ1的表达式为

(7)

式中:c为锚杆扩大头前端土体的黏聚力;Kp为扩大头前端土体的朗肯被动土压力系数，Kp=tan2(45°+φ/2)。以下将通过图3中莫尔圆的几何关系得到关于应力增量σT的表达式。

图3中左侧和右侧莫尔圆的圆心分别为O点和P点。假设右侧莫尔圆的半径为R，则有R=|PQ|=σ1-σP，而σP=(σA′+σC′)/2=γh(1+K0)/2+σT(1+ξ)/2，结合式(7)得

(8)

过圆心P做AC的平行线交CC′于D，则在三角形PDC′中

|DC′|=|CC′|-|CD|=|CC′|-|OP|=

|PC′|=R

∠PDC′=2α

运用余弦定理得

(9)

联立式(8)和(9)得到关于应力增量σT的一元二次表达式：

(10a)

其中系数

A=(ξKp)2-ξ(1+ξ)Kp+ξ

(10b)

(10c)

(10d)

应力增量σT应取其中有意义的实根。

端压力pD=σβ=σβ,0+σT，结合图3中C点正应力σβ,0的表达式得

(11)

(12)

此时图3中B点与C点重合，C′点与Q点重合，端压力pD取C′点的正应力值，即

(13)

这与之前研究中锚杆完全水平时的端压力表达式相同[15]。

(14)

此时图3中A点与B点重合，C′点与Q点重合，端压力pD取C′点的正应力值，即

(15)

这与之前研究中锚杆完全竖直时的端压力表达式相同[15]。

以上特殊情况(锚杆完全水平或完全竖直的情况)的端压力pD，也可以由式(10)和(11)直接得到。

1.3.2 静止土压力系数大于1的情况

当K0>1时，土体单元受力变化仍如图2所示。由于此时初始竖向应力σz,0=γh为小主应力，而σx,0=K0γh为大主应力，其莫尔应力圆与K0≤1的情况有较大不同，具体如图4所示。

图4 土体单元受力变化的莫尔圆(K0>1)Fig.4 Mohr′s circles for evolution of stress state for a soil element (K0>1)

A点和A′点分别代表α面的初始应力状态和最终应力状态，C点和C′点分别代表β面的初始应力状态和最终应力状态，B点代表与α面和β面均垂直的第3个面的初始应力状态。在图4左侧的初始莫尔应力圆中，B点的正应力K0γh为大主应力。在应力增量σT发生后，A′点、B′点和C′点分别代表3个相互垂直面的应力状态。由此可见，最终状态的大小主应力发生在A′点和C′点所构成的应力圆上，小主应力为S点的正应力，而大主应力为Q点的正应力。根据莫尔-库伦强度理论表达式，并在直角三角形A′TC′中运用勾股定理可得关于应力增量σT的一元二次表达式(16a)、(16b)、(16c)和(16d)。应力增量σT应取其中有意义的实根。

(16a)

其中

(16b)

(16c)

(16d)

端压力pD为C′点的正应力值，即

(17)

特别地，当锚杆完全水平时，α=0°，由式(16)和(17)得

(18)

(19)

当锚杆完全竖直时，α=90°，由式(16)和(17)得

(20)

(21)

注意到式(20)和(21)分别与式(14)和(15)相同，这是因为在这两种情况下，σz都从γh增大为大主应力γh+σT，而σx和σy是等同的，都从K0γh变为小主应力K0γh+ξσT。锚杆完全水平时的情况有所不同：当应力增量沿着水平方向X施加时，σy和σz是不等同的，因而式(18)、(19)与式(12)、(13)不同。

2 锚杆倾角的影响及算例

为了考察锚杆倾角的影响，定义一个比例函数f(α)，简称为锚杆端压力倾角比例函数，满足如下表达式

pD(α)=f(α)pD(α=0)

(22)

此处pD(α)为任意倾角α下的端压力，pD(α=0)为锚杆完全水平情况下的端压力。对于K0≤1的情况，pD(α=0)见式(13)，pD(α)见式(11)；而对于K0>1的情况，pD(α=0)见式(19)，pD(α)见式(17)。

借鉴曾庆义等[15]的工程实例参数考察锚杆倾角对锚杆抗拔力的影响。某基坑的3根锚杆，其锚杆参数和工况完全相同：埋深h=9 m，土层参数γ=18.8 kN/m3、c=60 kPa、φ=28°、τf=τdf=90 kPa，锚杆参数L1=4 m，D1=0.14 m，L2=4 m，D2=0.4 m。此处K0=1-sin(1.3φ)=0.41，而ξ=0.95Ka。据曾庆义等[15]报道，按锚杆完全水平计算所得的锚杆抗拔力为1 327.5 kN，远大于设计抗拔力670 kN和规程[16]的计算值663.3 kN。试验情况是其中两根锚杆加载到1 042 kN而没有破坏，另外一根锚杆加载到1 302 kN时钢绞线断裂一股，而扩大头前端土体还没有达到破坏状态。原设计方案采用普通锚杆时，其设计倾角为35°。

按上述例子，此处设计5个工况，其变化参数为c、φ和h，而其余参数与上述例子相同。注意到K0、Ka、Kp和ξ为φ的函数，随φ而变。对于K0≤1的情况，按式(6a)，当φ=28°时，K0=0.41；当φ=24°时，K0=0.48。对于K0>1的情况，假设超固结比ROC=12，根据式(6b)，当φ=28°时，K0=1.41；当φ=24°时，K0=1.67。各比较工况及相应锚杆水平或竖向时的端压力见表1。

表1 各比较工况及相应锚杆水平和竖向时的端压力Tab.1 Different working conditions and related earth pressures on the expanded end for horizontal and vertical ground anchors

由表1中工况1、2和3可知，锚杆水平时的端压力pD(α=0)随着扩大头前端土体黏聚力c的增大而增大；由工况4和2对比可知，端压力pD(α=0)随着扩大头前端土体内摩擦角φ的增大而增大；由工况2和5对比可知，端压力pD(α=0)随扩大头埋深h(或扩大头前端土体受到的地应力)的增大而增大。这可以从其物理意义得到解释。因为假设扩大头前端土体应力处于极限状态时符合莫尔-库伦强度准则，c、φ或h的增大都将使土体强度增大。如表1所示，锚杆竖向时的端压力pD(α=90°)也随扩大头前端土体黏聚力c的增大而增大，随扩大头埋深h的增大而增大；但是pD(α=90°)随φ的变化是增大还是变小，其情况不一定，因为此时随内摩擦角φ引起的各向异性因素(包括K0的变化)起较大作用。端压力pD(α)受锚杆倾角α的影响较大，其变化规律将在后面进行详细讨论。

由表1可知，当K0≤1时，各工况下锚杆水平时的端压力大于相应竖向时的端压力，这可从图3的莫尔应力圆得到解释。当锚杆水平时，α=0°，图中点C和C′分别与点B和Q相重合，应力增量σT=|CC′|较大；而当锚杆竖向时，α=90°，图中点C和C′分别与点T和Q相重合，应力增量σT=|CC′|相对小些。因为达到极限状态时，应力增量σT在端压力pD中占主导作用，锚杆水平时的端压力大于相应竖向时的端压力。相应地，由表1可知，当K0>1时，各工况下锚杆水平时的端压力小于相应竖向时的端压力，这可从图4的莫尔应力圆得到解释。其论述过程与当K0≤1时的情况类似，不再赘述。

当K0≤1时，根据式(11)、(13)和(22)可得锚杆端压力倾角比例函数f(α)，具体见图5。可以看出，各工况下，其锚杆端压力随着锚杆倾角的增大而减小，上述表1显示的锚杆水平时的端压力大于相应竖向时的端压力是f(α)曲线两端点大小的情况。并且，锚杆倾角对f(α)的影响较大，在工况1黏聚力c为0时，f(α)在α=90°时为0.24，即此时的竖向端压力仅为其相应水平端压力的0.24倍。对比工况1、2和3可知，随着黏聚力c的增大，其f(α)的减缓速率变小。这是由于黏聚力c是各向同性的，当黏聚力占主导作用时，如黏聚力取较大值60 kPa时，由内摩擦角引起的各向异性因素K0、Ka和Kp及由倾角引起的各向异性便不占主要作用。对比工况2和4可知，随着内摩擦角φ的减小，其f(α)的减缓速率稍有变小。这是因为随内摩擦角φ的减小，由内摩擦角引起的各向异性因素(Ka、Kp和K0)的影响均有所减小。对比工况2和5可知，随着埋深h的增大，其f(α)的减缓速率变大。这可能是由于随着埋深的增大，由地应力和内摩擦角引起的各向异性因素起较大作用。

图5中扩大头锚杆端压力随着锚杆倾角增大而减小的规律，与板式锚杆板前土压力在常规砂土中的表现规律一致[9-10,13]。此处的f(α)包含黏聚力和内摩擦角等土体性质参数，因而能从力学机制层面对端压力的变化规律进行解释，同时能给工程实践提供理论指导。

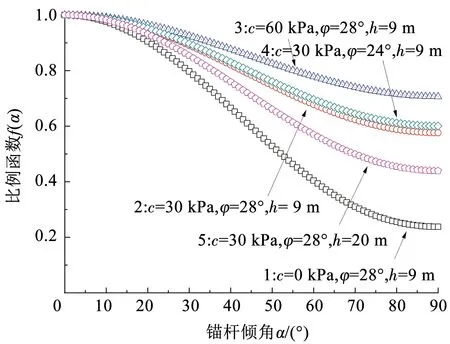
图5 各工况下锚杆抗拔力倾角比例函数(K0≤1)Fig.5 Ratio function of pullout capacity with inclined angle for end-expanded anchors under different working conditions (K0≤1)

当K0>1时，根据式(17)、(19)和(22)可得锚杆抗拔力倾角比例函数f(α)，具体见图6。

图6 各工况下锚杆抗拔力倾角比例函数(K0>1)Fig.6 Ratio function of pullout capacity with inclined angle for end-expanded anchors under different working conditions (K0>1)

由图6可以看出，各工况下，其锚杆端压力随着锚杆倾角的增大而增大，且锚杆倾角的影响较大。在工况4内摩擦角φ为24°时，f(α)在α=90°时为2.67，即此时的竖向端压力为其相应的水平端压力的2.67倍。对比工况1、2和3可知，随着黏聚力c的增大，其f(α)的增大速率变小。这是由于黏聚力c是各向同性的且其占主导作用时，锚杆倾角的影响将减弱。对比工况2和4可知，随着内摩擦角φ的减小，其f(α)的增加速率变大较多。此处与K0≤1时f(α)变化不敏感的情况较为不同。随内摩擦角φ的减小，由内摩擦角引起的各向异性因素各自变化。其中Ka和Kp的影响减小，但是K0由φ=28°时的1.41变为φ=24°时的1.67，变化较大且在各向异性因素中占主要作用。因此，各种各向异性因素综合作用的结果使得f(α)的增加速率变大。对比工况2和5可知，随着埋深h的增大，其f(α)的增加速率变大。这可能是因为由地应力和内摩擦角引起的各向异性因素起较大作用。

由锚杆抗拔力公式(1)～(4)可知，端压力pD仅影响T3部分的抗拔力，对T1和T2部分没有影响。对于T3随锚杆倾角的变化同样满足T3(α)=f(α)T3(α=0)，即如图5、6所示的情况。仍然取曾庆义等[15]工作中的参数，得到表1各个工况下锚杆的极限抗拔力各分量与总量，如表2所示。

表2 各工况下锚杆的极限抗拔力各分量与总量Tab.2 Total ultimate pullout force and its components for ground anchors under different working conditions kN

由表2可知，各个工况下，锚杆倾角对T3的影响较大，对T有一定的影响。当K0≤1时，T随锚杆倾角的增大而减小；当K0>1时，T随锚杆倾角的增大而增大。值得注意的是，L1是锚杆普通锚固段的计算长度，对于非预应力锚杆，常取实际长度减去两倍扩大头直径；对预应力锚杆，取值为0[17]。郭钢等[3]关于砂土中扩体锚杆承载力特性模型试验的研究表明：普通锚固段相比扩体锚固段，与其周围土体之间通常先产生界面剪切破坏，而扩大头端压力因土体硬化可以持续加强。因此，在实际应用时，T1可能会更小，T3对T的贡献可能会更大，因而锚杆倾角对T的影响比较大。

对于常见的K0≤1的情况(见图5)，如果将倾斜锚杆的抗拔力取值为完全水平锚杆的抗拔力，其理论取值将偏大，在工程上或偏于不安全。但当锚杆倾角较小时，或可以采用锚杆完全水平时的解来估算土体对倾斜锚杆扩大头端部正压力所提供的抗拔力T3。比如，图5中各工况，在倾角小于20°时，T3的误差在10%以内。类似地，对于K0>1的情况，如果将倾斜锚杆的抗拔力取值为完全水平锚杆的抗拔力，其理论取值将偏小。图6中各工况，在倾角小于20°时，T3的误差在19%以内。

对端压力公式(11)和(17)进行进一步的说明。曾庆义等[15]给出了土体K0≤1时扩大头锚杆完全水平或完全竖直情况下的极限端压力，是本研究极限端压力公式的两个极端情况，而其他锚杆倾角下的端压力介于这两者之间。本研究分别讨论了土体K0≤1和K0>1的情况，因而研究成果对任意K0的土体均适用。对于常规土体(K0≤1的情况)，扩大头锚杆极限端压力与前人研究[9-10,13]中板式锚杆板前土压力随锚杆倾角的变化规律相一致，在定性层面上说明本文公式的正确性；关于扩大头锚杆极限端压力随倾角变化的相关实测数据还较为缺乏。而对于特殊土体(K0>1的情况)，相应的试验数据更为缺乏。将本文的抗拔力理论解析解与各种情况实际试验结果(或数值模拟结果)进行广泛深入的对比研究，是未来急需进行的工作。