一种自适应分数阶变分图像复原模型

徐慧娴,田洋川,陈明举,2*，熊兴中

(1.四川轻化工大学 人工智能四川省重点实验室，四川 宜宾 644000；2.四川轻化工大学 企业信息化与物联网测控技术四川省高校重点实验室，四川 宜宾644000)

0 引言

图像在获取、传输和存储过程中不可避免地会受到不利因素的影响，造成质量退化。后期应用中往往需要高质量的清晰图像，这就要求图像复原技术尽可能地恢复出真实的原始图像[1]。图像复原问题是一个病态问题，通过求解Tikhonov正则化[2]，对原始函数的估计正则化函数采用全变分模型可以较好地去除图像的模糊，复原图像的真实信息[3]。近年来，产生了许多经典的基于变分技术的图像复原模型，如异向全变分模型[4]、高阶变分模型[5]以及非局部变分模型[6]等。通常，变分模型都是基于整数阶微分梯度，整数阶梯度不能有效地区分图像高频信息与干扰噪声，在图像复原过程中，部分噪声被当作图像高频信息进行增强处理，产生阶梯现象，造成图像模糊。

为抑制阶梯效应并更好地复原图像纹理信息，相关研究发现分数阶微分具有“弱导数”的性质，对不同频域成分采用不同的处理策略，在增强图像高频信息的同时，能够较好地保留图像中的低频信息[7-8]。将分数阶微分引入变分模型中，势必提高变分技术图像增强的性能。Chowdhury等[9]根据图像的特性，建立去除泊松噪声的分数阶变分模型，有效地克服了阶梯现象。王迎美等[10]将分数阶与整数阶变分(Integer and Fractional Order Total Variation,IFOTV)相结合，分别极小化分数阶与整数阶的梯度，实现噪声的消除，有效地克服了阶梯现象。Fairag等[11]通过分数阶代替图像复原变分模型的变分项，建立分数阶的图像复原变分模型(Fractional Order Total Variation,FOTV)，以获得更好的图像去模糊性能。

利用分数阶变分非线性特性，可以有效识别图像的不同频域成分信息，实现图像细节与纹理的高效复原，从而获得更好的图像处理效果。但分数阶变分技术在图像复原处理中仍存在一定的不足，未充分考虑图像局部特性[12]，在不同特性的区域采用恒定的图像修复策略，欠缺对退化函数先验知识的有效利用与优化求解困难等[13-14]。

针对上述问题，本文在分数阶图像复原模型的基础上，提出了一种充分利用退化函数先验信息的自适应分数阶图像复原模型。该模型首先引入图像梯度算子控制模型的分数阶变分项，以实现在图像不同特征区域采用不同的分数阶变分策略和变分阶数的自适应；通过极小化退化函数分数阶范数，实现退化函数的平滑先验知识的有效利用。然后，将对偶算法引入交替极小化算法中[15]，实现模型的优化求解，从而实现对原始图像的准确估计。最后，通过对比实验证明，建立的自适应分数阶图像复原模型可以更好地复原图像的结构与纹理信息，图像复原性能更优。

1 相关理论

1.1 分数阶变分模型

Wei等[16]将整数n阶扩展到整个实数空间，引入伽马函数Γ(n)，得出连续函数f(t)任意阶次α的分数阶:

(1)

式中,α为任意实数阶次；h为微分步长；[]为取整符号；Γ(n)为伽马函数；t和a分别表示m的取值范围。在图像全变分模型中将分数阶微分算子代替整数阶微分算子，可得分数阶变分模型：

(2)

(3)

(4)

将分数阶代入正则化模型，得到图像复原的分数阶变分模型FOTV:

(5)

1.2 Bregman迭代与对偶算法

直接通过极小化图像梯度的能量泛函通常存在不稳定现象，Bregman迭代与对偶算法能有效地消除变分求解过程中的不稳定现象，从而快速迭代实现收敛。本文采用分裂Bregman迭代交替极小化的思路[17]，将对偶算法引入交替极小化算法，实现模型的优化求解。

Bregman迭代引入次梯度算法，并通过极小化图像的Bregman距离实现图像能量泛函的求解。令：

J(u)=‖αu‖1。

(6)

图像u与un的分数阶Bregman距离定义为：

(7)

通过FOTV极小化问题转化为极小化Bregman距离:

(8)

另一方面，对偶算法(Primal Dual,PD)可以消除图像的鞍点[18]，有利于变分求解的稳定。定义分数阶对偶算子为：

(9)

式中，

(10)

FOTV模型采用对偶算法的极小最大值法转化为：

(11)

2 自适应分数阶变分复原模型

2.1 自适应分数阶变分复原模型的建立

由式(5)可以看出，分数阶变分模型在图像的不同区域都采用权重恒定的分数阶变分项，未能根据图像的局部特性进行相应调整。另外，分数阶变分模型未充分利用退化函数的特性，若充分利用退化函数的先验知识，其复原性能将进一步提高[19]。

基于上述思想，采用l1范数对退化函数的分数阶梯度进行表示，并通过梯度大小控制分数阶变分项的阶数，构建图像复原的自适应分数阶变分 (Adaptive Fraction-Order Total Variation,AFOTV)模型：

(12)

式中，g(u)为权值，大小由图像局部梯度确定：

(13)

由式(13)可知，g(u)大小由图像的梯度决定。在图像平滑区域，其值较大，着重于模糊的去除；在图像边界区域，其值较小，着重于图像信息的保持，从而实现在图像的不同特性区域采用不同的分数阶策略，可以更好地复原图像的真实信息。另外，式(13)中加入对退化函数进行分数阶描述，对于常见的退化函数，如滤波卷积、运动模糊以及大气湍流等，其梯度泛函值较小，增加了对退化函数k的分数阶先验知识的利用，可以进一步提高复原图像的质量。

2.2 模型的求解

为了实现AFOTV模型的稳定迭代求解，采用分裂迭代(Split Bregman,SB)交替极小化思想，引入辅助变量ω，AFOTV模型极小化问题可转化为：

(14)

(15)

ωn+1=ωn+f-kωn+1。

(16)

引入对偶算子的思想u与k的极小化问题可以进一步转换为：

(17)

(18)

利用对偶算子分别求解式(17)和式(18)，可得：

(19)

un+1=un-τ1[λ1(α)Tpn+1+(kn)T(knun-f-ωn)]，

(20)

(21)

(22)

kn+1=kn-τ2[λ1(α)Tqn+1+(un+1)T*(knun+1-f-ωn)]，

(23)

式(19)和式(20)中∏X(z)，∏Y(z)表达式分别为：

(24)

(25)

综上分析，AFOTV模型的PD+SB迭代求解流程如下：

3 结果与讨论

为了证明AFOTV模型的性能，将AFOTV图像复原的结果与FOTV，IFOTV进行对比分析实验，采用峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似性(Structural Similarity Index,SSIM)作为评价指标。

为了使分数阶α的取值最优，首先在常见的退化环境下(高斯模糊、均值模糊以及移动模糊)对α取不同的值进行实验，选择最优α进行下一步对比分析，结果如图1所示。由图1可以看出，对于高斯模糊、均值模糊以及移动模糊α取值为1.6，1.8，1.6时，获得最大的PSNR值。

图1 分数阶α取不同值时对cameraman图像复原性能的影响Fig.1 Influence of the fractional orders α on the restoration performance of a cameraman image

为了进一步说明AFOTV模型具有更好的图像复原性能，图2～图4给出了cameraman，woman以及boat图像在高斯、均值以及运动退化环境下采用3种模型复原后的结果，并在各图的右下角给出红色区域的局部放大图。

(a) 原图

由图2可以看出，在高斯退化环境下，经过FOTV复原的图片存在一定程度的失真现象，细节信息也存在一定的模糊。IFOTV对边缘信息的损失严重，人脸、相机及衣角的边缘模糊。而本文的AFOTV模型不存在图像失真现象，并且能更好地复原图像的细节纹理信息，人脸、相机及衣角的轮廓都更为清晰，视觉质量最佳。由图3可以看出，在均值退化环境下，FOTV及IFOTV复原后的图片中，眼窝、鼻梁及头发阴影部分的失真较大，并且边缘存在一定程度的模糊，而AFOTV对眉毛以及眼睛轮廓的复原效果最好。由图4可以看出，在运动退化环境下，AFOTV可以更好地复原图像的细节纹理信息，文字更加清晰，边界轮廓也处理得更好。综上分析可知，在3种退化环境下，AFOTV模型在采用分数变分描述退化函数的同时实现对图像分数阶变分的自适应，更准确地实现对图像的描述，获得了更好的图像复原性能。

表1给出了图2～图4中复原前后各图片的PSNR与SSIM。由表1可以看出，FOTV复原后的图像的PSNR和SSIM最低，AFOTV模型图像复原后的PSNR和SSIM最高，其PSNR和SSIM分别高于IFOTV 0.5 dB和0.01 dB。由客观指标可以看出，AFOTV模型在对退化函数分数阶变分描述的同时通过图像梯度实现自适应分数阶变分，有效利用图像的先验知识，获得更好的图像复原性能。

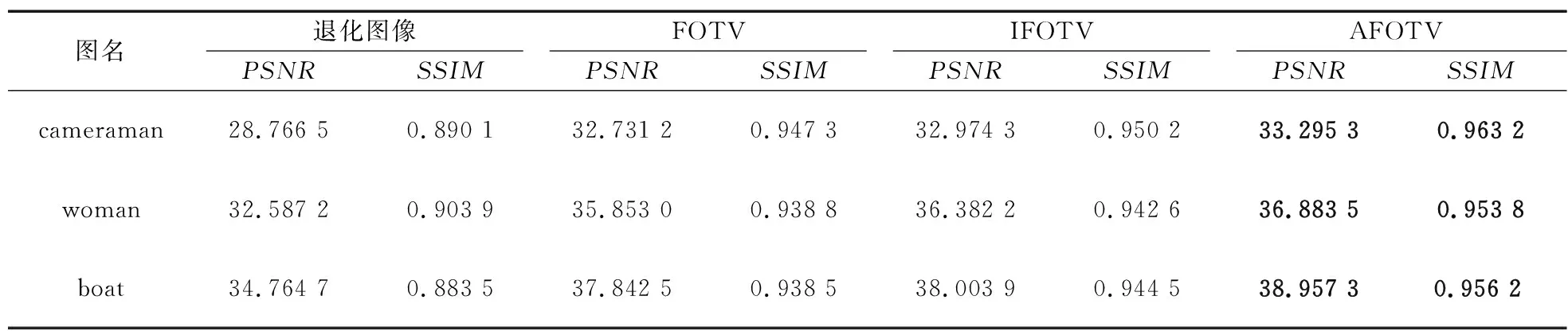
表1 不同退化图片采用3种模型复原后性能比较

4 结束语

本文建立了一种自适应分数阶图像复原模型，采用图像梯度的算子对分数阶变分项进行修正，以实现在图像不同特性区域进行不同程度的变分复原；对退化函数采用分数阶变分进行描述，以更好地利用退化先验知识实现对原始图像的估计。在模型的求解中，通过结合Bregman迭代与对偶极小化实现建立的自适应分数阶图像复原模型优化求解，并通过对比实验证明该模型具有更好的图像复原性能，能更好地复原图像的结构与纹理信息。因此，自适应分数阶图像复原模型具有很好的参考价值与应用前景。

由于新模型的建立是假设退化函数梯度的泛函较小的前提，对于高斯模糊、均值模糊以及移动模糊退化复合上述假设，对于其他退化环境，如大气湍流退化、辐射退化以及多种复合退化场景，本模型的适用性还有待进一步研究。另外，模型的求解采用Bregman迭代与对偶极小化实现，该方法涉及多个变量的极小化，迭代收敛时间较长，下一步将新的数学理论应用于模型的求解中，以缩短收敛时间。