水资源需求重大改变后的效能保障策略研究

郭建斌，梁 翔，杨 沾

（河海大学能源与电气学院，南京 211100）

0 引 言

近年来随着民生用水需求的日益增加，受制于自然水资源和工程设计等固有条件限制，水资源发电用水普遍面临巨大挑战，兼顾民生与发电用水需求的调度策略成为保障工程高效运行的重要技术手段。

调度图方法是水库运行的常规技术手段，其成果较多表现为可行解而非最优解［1-3］，不能满足多目标工程问题的最优解决。近年来，遗传算法、粒子群算法、蝙蝠算法等计算方法大规模应用于工程优化问题［4-7］其中快速非支配排序遗传算法（NSGA-Ⅱ算法，下同）通过种群杂合、精英化策略和拥挤度比选等措施促进了多目标最优解的获取，具备复杂非劣排序遗传算法的适应性和快速收敛的优点，日渐成为工程多目标寻优任务的常用算法。王学斌等应用NSGA-Ⅱ算法制定了黄河下游生态、综合供水和发电效益之间多目标共赢的调度策略，形成了不对称竞争关系的协同效益最大［8］；方国华等通过NSGA-Ⅱ算法制定了平衡生态保护和发电量的优化调度策略，试图通过少量降低发电量促进下游河段生态环境保护等多目标的综合最优［10］；Alahdin 等应用NSGA-Ⅱ算法制定了梯形水库群水资源分配和发电量的多目标优化调度策略，实现了三座梯形水库水资源高效利用和发电效益的多目标综合最优［11，12］。可以知道，用水需求重大变化背景下，应用NSGA-Ⅱ算法寻求多目标最优的调度策略，能够均衡在役水库民生、发电等用水多目标的相互竞争问题，从而提高水资源综合利用效益，减缓水资源短缺面临的瓶颈效应，具有重要的工程与现实意义。

1 基于NSGA-Ⅱ算法的水库多目标优化调度模型

1.1 水库多目标优化调度模型

水库多目标优化调度策略模型，呈现各目标既非完全对立也非完全协调的特征［10］，即某一目标效益增加可能造成其他目标效益增加或减少［13］，优化算法实现各目标之间分配和协调策略［14］成为工程运行增效的重要研究内容。在多目标优化问题的求解中，很难找到一个真正意义上的单一最优解，最终的目标值会输出一系列可行解，称之为非支配解（Pareto 解），这些可行解的集合为Pareto最优解集［15］。

模型通过决策最优建立多目标函数，按照约束条件开展水资源需求的递归比选，获取最优调度策略。水库多目标优化调度模型按图1 所示构建，目标函数和边界约束条件按式（1）、式（2）、式（3）所示（含水量平衡约束和供水保障约束）建立关联关系。

图1 水库多目标调度模型图Fig.1 Multi-objective dispatching model diagram of reservoir

式中：W 为调度期内水资源综合利用目标函数，f 为子目标函数集合，W1，W2，W3，…，Wn为水 资 源利用子目标函数；V|(t)、V|(t + 1)分别为水库t 时段、t+1 时段蓄水量，m3；Qin|(t)、Qout|(t)分别为水库t 时段入库流量、下泄流量，m3∕s；Δt 为计算时段长度；D|(t)、S|(t)分别为水库下游t 时段的需水量和供水量，m3；t、T 分别为调度期内时段编号和总时段数；λ 为水库下游的用水保证率。

1.2 水库运行策略的优劣度量

工程一般对发电、供水等多目标较为关注，水资源调度策略优劣可简化为民生缺水、发电缺水度的整体综合最优。为了更好对水库运行策略的优劣进行评定，以综合保障需水产生的发电效益增长来确立综合最优评价指标η，按照相对民生缺水度增加发电量的程度进行定义，表征单位民生缺水度变化对发电增加量的影响程度，是水资源运行策略优劣的无量纲度量［按式（4）所示］，一般选取η 大于1 的运行策略。其中缺水度［16］，采用最小二乘法平方和形式［17］呈现水资源用水需求面临的挑战，取。

式中：η 为综合最优评价指标；E、Ea分别为策略发电量Q|(t)· H|(t)·Δt 和实际运行方案发电量，GWh，其中，k 为出力系数；WS_D、和Wa分别为策略民生缺水度和实际运行方案民生缺水度。

1.3 NSGA-Ⅱ算法

NSGA-Ⅱ算法是获取水库多目标优化调度策略的常用手段，应用NSGA-Ⅱ算法的多目标优化调度计算流程见图2 所示，设置决策变量生成种群，操作交叉、变异、快速非支配排序和拥挤度距离计算等内容，按照约束条件对中间值和目标值迭代计算和比选，并通过惩罚函数omega 和惩罚因子c 对目标函数WS_D|(t)、E|(t)进行补偿［见式（5）所示］。

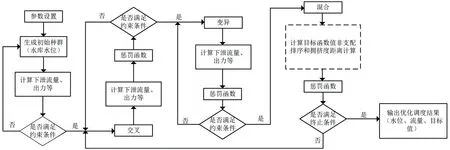
图2 应用NSGA-Ⅱ算法的水库多目标优化调度计算流程Fig.2 The calculation process of reservoir multi-objective optimal dispatching using NSGA-Ⅱ

决策变量的选择一般以水库运行中对各运行参数起到广泛影响的变量为依据。本文所选取的水位是水库运行中重要的组成部分，是有效反应水库不同时段之间变化的直观表现。以水位作为决策变量，可形成水库优化调度计算的闭环，从而更好地输出最优调度策略。

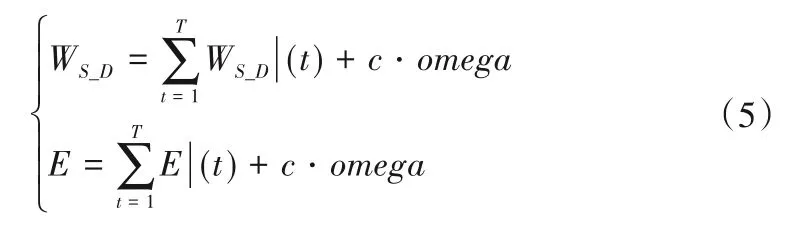
式中：WS_D|(t)、E|(t)为民生缺水度、发电量目标函数；c、omega为惩罚因子、惩罚函数。

2 需求改变后工程效能保障策略

广东某水库位于乳源县的南水河，属于多年调节水库。近年来，随着水库民生用水激增，水库需求发生重大改变，兼顾民生、发电等多目标用水竞争的策略，成为保障水资源效能高效利用的重要工程软技术手段。根据水库历史资料，选取典型蓄放水调度周期（2005年3月-2008年1月），共35 个计算时段。调度期内水资源实际运行方案的整体民生缺水度为15.67、总发电量为702.14 GWh。相关数据列见表1，水库历时曲线见图3所示。

表1 典型调度周期入库流量表Tab.1 Inbound flow meter for typical dispatch period

图3 典型调度周期流量水位变化图Fig.3 Flow and water level changes in a typical dispatch cycle

2.1 水库优化调度策略

应用NSGA-Ⅱ算法开展优化调度策略研究。其中调度策略模型的种群规模为30，最大迭代次数取1 000次，交叉概率为0.95，变异概率为0.05，惩罚因子c 为20，出力系数k 为8.1。计算所得Pareto 最优解集由缺水度和发电量组成，现将30 组最优解集由综合最优评价指标η分布形式呈现，见图4所示。

图4 Pareto最优解集按综合最优指标分布图Fig.4 Pareto optimal solution set according to the comprehensive optimal index distribution diagram

Pareto 最优解集编号按整体民生缺水度数值大小升序排列。如图4 所示，顶部策略整体民生缺水度大于实际运行方案整体民生缺水度，呈现综合最优评价指标过大的特点。以该策略为界限，考虑整体民生缺水度小于实际运行方案整体民生缺水度，按照综合最优评价指标η值大于1的先行定义，获取虚线框中调度策略Ⅰ～Ⅳ，其数据列见表2。

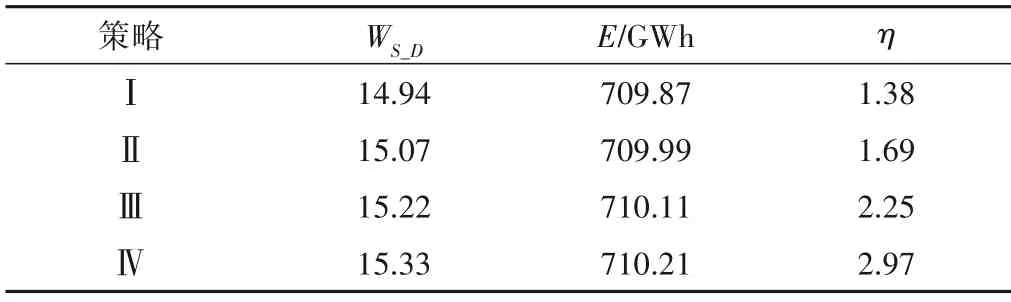
表2 最优调度策略相关数据Tab.2 Related data of optimal scheduling strategy

为直观反映策略Ⅰ～Ⅳ对民生、发电用水的兼顾程度，建立逐月民生缺水度、发电量与实际运行方案对比见图5、6所示，以及各策略水位调度图见图7所示。

图5 逐月民生缺水度对比图Fig.5 Comparison of the water shortage of the people's livelihood by month

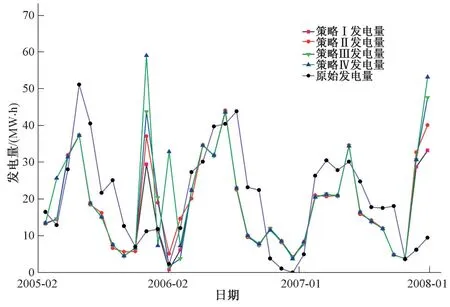
图6 逐月发电量对比图Fig.6 Comparison of the monthly power generation

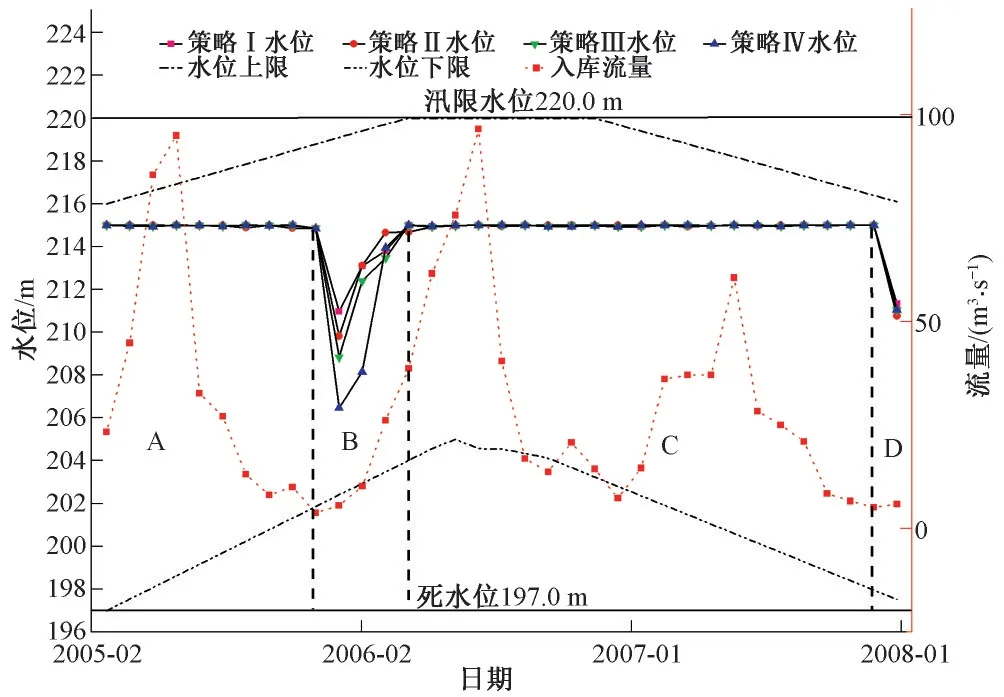
图7 水位调度图Fig.7 Water level scheduling diagram

2.2 调度策略评估与分析

（1）策略Ⅰ～Ⅳ兼顾了民生与发电用水需求。其中B 区（2005年12月-2006年4月）、D 区（2007年12月-2008年1月）两段调度期内充分利用较高库水位条件，尽可能多安排发电用水计划，其他时段内（A 区、C 区），以保障民生用水为主，尽可能减少水资源消耗，甚至不发电，呈现积蓄水资源抬升库水位的特点。由水位调度图可以知道，4 种策略用水均受入库流量影响不大，减少了电站对自然水资源的依赖度。

（2）与现行运行方案相比，策略Ⅰ～Ⅳ发电量分别增加了7.73、7.85、7.97、8.07 GWh，对应民生缺水度分别下降了4.66%、3.83%、2.87%、2.17%。相对于实际运行方案，调度策略Ⅰ～Ⅳ不仅使民生用水的缺水度得到有效遏制，又提高发电量，使水资源利用的整体效能得到更好利用。

3 结 语

水资源需求发生重大改变的时空背景下，建立了应用NSGA-Ⅱ算法的水库运行多目标优化调度模型，以工程实际水库为对象进行了示例研究，利用综合最优评价指标η 对调度策略进行了优劣评定，主要结论如下。

（1）以缺水度及发电量定义的综合最优评价指标η，可以对多目标优化的Pareto 解集进一步最优选取，有效选择出了兼顾民生与发电用水需求的调度策略，具有一定的工程实际参考价值。

（2）通过实例验证，获取的最优调度策略Ⅰ～Ⅳ既减缓了水资源面临的短缺，又充分利用了水资源效能，使得工程经济效益得到了明显改善。 □