一维卷积长短期记忆神经网络的管道泄漏检测方法

2022-01-24刘伯相冉义建

中国农村水利水电 2022年1期

聂维，江竹，刘伯相，林豪，冉义建

（西华大学能源与动力工程学院，成都 630019）

0 引言

输水管道是现代化建设的基础设施之一，管道服役过程中遭受多种内外因素影响会引发的泄漏、损坏等故障，造成难以挽回的经济损失和安全事故，甚至会带来环境污染等问题。毋庸置疑的是输水管道泄漏检测技术在工程应用中彰显着重要意义［1］。目前常用的泄漏检测方法主要分为管外和管内两种检测法，管外检测法主要依靠人工巡检，存在检测效果差且人物力浪费较大等问题；而管内检测法主要分析管内压力、流量和温度等数据，反馈结果的准确性较之增加。其中，以管内压力数据为驱动的检测方法有着可靠性强、检测距离远、便于工程实施等诸多优点而被得到广泛应用［2］，该类方法主要依靠传感器采集信号，应用支持向量机［3］、BP神经网络［4］等人工智能方法提取和筛分信号的演变特征［5］，实现泄漏检测的目的。但这类传统的智能识别方法［6-8］，多是基于浅层网络的学习，尚不具备学习复杂非线性关系的能力，以至于泄漏检测的精度分析亟待提升。

近年来，可挖掘数据深层特征的深度学习算法已成功应用于许多领域中，尤其是卷积神经网络（Convolutional Neural Networks，CNN）和循环神经网络（Recurrent neural network，RNN）都已取得了令人瞩目的成绩［9，10］。CNN 具有超强的空间特征提取能力，在管道泄漏检测中的应用也逐渐成熟。分析发现，CNN 实现泄漏检测一般分两种，其一是直接利用一维卷积神经网络（1-Dimensional Convolutional Neural Networks）学习数据中的泄漏信息，Cai 等［11］便是通过一维CNN 学习方法实现了管道的泄漏检测。此外，变换方式将原始信号转化为二维矩阵，CNN 再从中抓取泄漏特征实现学习计算。宁方立等［12］利用二维时频图作为输入的CNN 对泄漏特征进行学习。Hu 等［13］通过转换CNN 模型中数据协方差矩阵的最大特征向量，准确提取了泄漏特征参数进而判断管道状态。Zhou 等［14］提出了一种基于卷积神经网络的泄漏检测图像识别方法，能较好地解决不同泄漏孔径或位置特征高度相似的问题。但这些方法在对信号进行特征提取的过程中仅仅考虑了数据的局部空间分布特性，而忽略了数据在时序上的演化特性，反映了数据一维分布处理分析的局限性。

管道压力信号作为一维时间序列，其泄漏特征除表现在局部空间，在时间维度上亦有所体现。因此，仅靠CNN 难以全面捕捉泄漏信号的时变趋势。值得一提的是长短期记忆网络（Long Short-Term Memory，LSTM）作为一种改良的循环神经网络，在时域方面展现出的强学习能力，弥补了CNN 单独使用时泄漏检测的不足［15］。因此，为了进一步提升管道泄漏检测分析反馈精度，本文将卷积神经网络和长短期记忆网络相结合，建立一维卷积长短期记忆神经网络（1D-CNN-LSTM）。基于这一网络模型的方法，将去噪后的管道压力信号作为输入，先后利用CNN 和LSTM 提取其局部空间上和时间维度上的演变特征，找到管道压力信号与管道状态之间的对应关系，实现管道泄漏的准确检测。

1 基础理论

1.1 一维卷积神经网络

卷积神经网络（CNN）是一种深度前馈神经网络，其典型结构由输入层、卷积层、池化层与全连接层构成。一维卷积神经网络是指在一维数据上进行卷积和池化等操作，其结构如图1所示。CNN 实际上是通过建立多个滤波器来提取数据的局部特征，多网络层数可提取到更深层次的数据特征，最后得到具有平移旋转不变性的鲁棒特征［16］。泄漏发生时，管道内压力下降，表现出明显的局部空间特性［17］，利用CNN 可实现有效提取其局部特征，完成数据的收敛分析。

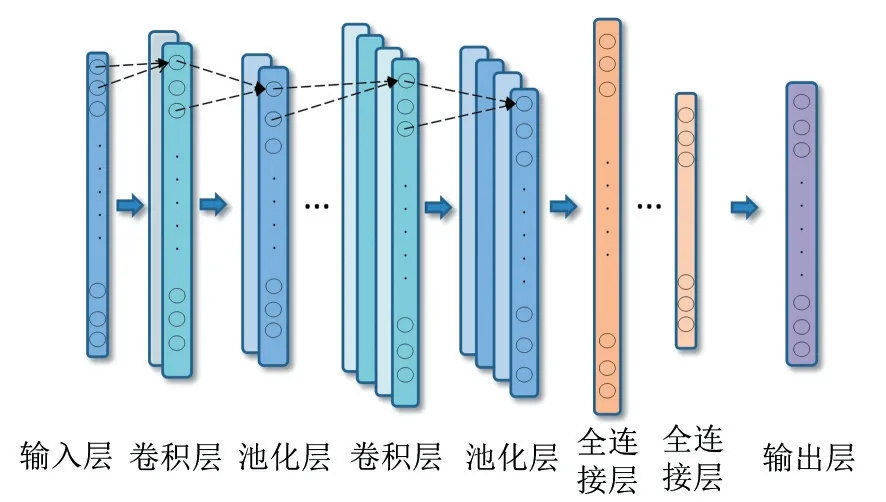
图1 一维卷积神经网络结构Fig.1 1-Dimensional convolutional neural network structures

CNN 在提取特征过程中，卷积层和池化层交叉排列形成卷积组，逐步提取信号特征。在卷积层中，前一层的输出由卷积核进行卷积操作，利用激活函数输出特征矢量。一维卷积的数学模型可描述为：

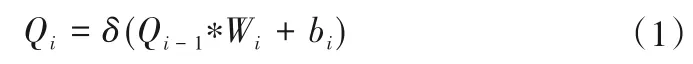
式中：*表示卷积操作；Qi-1和Qi分别表示卷积前后的特征量；bi和Wi表示的是第i层卷积核的偏置向量和权重矩阵；δ表示激活函数。

卷积操作是为了建立层与层之间的映射关系。池化层对卷积后的数据进行降维操作，可以进一步提取不同范围的特征以及减小计算量。其计算过程表示为：

式中：ys-1和ys分别表示第s层池化的输入和输出；pool()表示池化函数。最大池化和平均池化是常用的池化方式。

1.2 长短期记忆网络

LSTM 是一类改进的循环神经网络［18］，其结构包括输入层、隐藏层和输出层，由于隐藏层的各神经单元中加入了记忆单元，可以控制时间序列上的信息被遗忘或输出，解决了RNN 中梯度爆炸和梯度消失的问题，在处理长序列数据时远比RNN表现得优异。本研究所用数据为管道内的时域压力信号，其时间序列上的特征信息能够有效地被LSTM 提取。t时刻LSTM 网络的单元结构如图2所示。

图2 LSTM 网络结构Fig.2 LSTM network structure

在LSTM 单元中有3 种不同的门控，其中，输入门控制当前输入数据流入记忆单元的方式，遗忘门筛分历史信息并决定部分信息将会被丢弃，输出门控制记忆单元对当前输出值的影响，门控的耦合作用实现了LSTM 对信息的储存和更新。首先，遗忘门根据上一时刻的隐藏状态ht-1和新输入数据xt来判断是否保留先前单元状态信息：

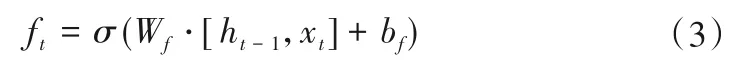
然后，输入门从ht-1和xt计算获得的信息及本单元所需保存的状态：

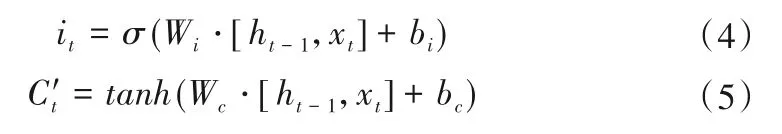
接下来更新单元状态，更新后单元状态由保留的先前单元状态加上本单元状态信息所得：

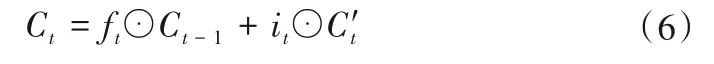
最后，由输出门和单元状态计算输出：

式中：it、ft、ot分别表示LSTM 中第t个单元的输入门、遗忘门和输出门；⊙代表逐个元素相乘；xt为t 时刻的输入；ht为t 时刻单元的输出；C′t、Ct分别表示隐藏状态和更新后的单元状态；Wf、Wo、Wi、bf、bo、bi为对应门控的权重矩阵与偏置向量；σ、tanh表示两种激活函数。

在管道泄漏检测中，需建立多对一形式的LSTM 模型，即输入到LSTM 网络的为序列数据，最后一个输出ht作为管道泄漏检测的结果。

1.3 基于1D-CNN-LSTM 的管道泄漏识别模型

针对管道泄漏的压力数据同时拥有局部特征和时间序列特征，本文提出1D-CNN-LSTM 神经网络模型来检测管道泄漏，其网络结构如图3 所示。该模型由一维CNN 和LSTM 组合而成，泄漏压力信号深层空间特征和时间维度的特征信息能被其有效提取。首先，CNN 从压力信号数据中自适应提取泄漏局部特征后，考虑到管道压力信号在时间维度上的相关性，用LSTM继续对CNN 提取到的特征量进行二次特征提取，获取特征的时序信息。随后通过全连接层将特征量维度降至与分类数相同，再使用Softmax分类器完成特征分类，以检测管道是否泄漏。

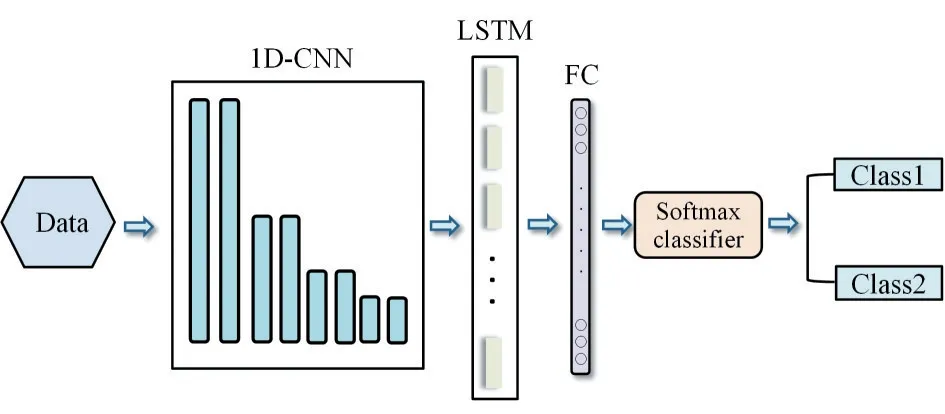
图3 1D-CNN-LSTM 网络结构Fig.3 1D-CNN-LSTM network structure

理论上，提取到的数据特征与网络层数呈正比关系，即网络层数越多，网络深度越高，能够提取到更多的特征；但复杂度也会随之增加，训练困难度上升，并伴随着网络过拟合的风险，因此选择合适的网络层数是提高网络性能的关键。为得到该模型的最优结构和参数，需要不断地训练网络，具体流程如图4所示。将采集到的数据打乱分为训练集和测试集，训练集用来训练网络得到网络的各项内置参数，在训练期间的每次迭代过程中前向计算出损失函数，再根据误差反向传播算法更新参数，经过多次迭代之后得到训练完毕的网络，而后将测试集代入该网络中测试网络的分类效果，若网络的损失或分类准确率不满足要求，说明网络的结构或参数设置不合理，则需修改模型再次进行训练，直到损失和准确率满足要求。其中分类准确率为分类正确的样本数与总样本数之比。网络损失为交叉熵损失函数，其数学定义如下：

图4 本文方法处理流程Fig.4 Process of the method in this paper

式中：y′表示目标概率分布；y表示输出概率分布。

2 实验验证

2.1 数据获取与处理

2.1.1 数据采集

为了验证所提基于1D-CNN-LSTM 神经网络方法对管道泄露检测的有效性和可行性，选取真实管道就传统方法进行对比分析试验。实验管道的分布结构如图5 所示，其中水源由城市消防栓开阀供给，消防栓出口设有压力计，显示压力稳定在约1.6 bar。实验管道与消防栓用长5 m 的消防带相连。实验管道总长18 m，内径80 mm，壁厚4 mm，末端封闭，管身材质为Q235B 钢。管道安装有四个水龙头，用以模拟不同位置的漏点，控制水龙头的开度模拟不同大小的泄漏，设定了a、b、c、d、e五种开度，分别对应的漏点面积是0.5、2、3、5、8 mm²。

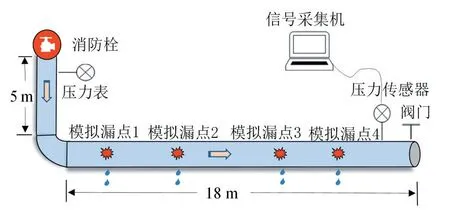
图5 实验管道示意图Fig.5 Diagram of experimental piping

采集泄漏信号时，快速打开某一模拟漏点，获取在泄漏产生前后时间段的管道压力数据；各模拟漏点对每一种开度模拟五次泄漏处理，采样频率为500 Hz，共采集100 组泄漏数据，每组泄漏信号的采集间隔为3 min；正常工况下的数据采集采用连续不间断采集方法，采集完成后再依次分割成100组数据，以漏点1 为例，采集到的不同模拟漏点开度情况下及无泄漏情况下的压力信号分布如图6 所示。由图可知，无泄漏时的管道压力在一定范围内小幅波动，但总体平稳，呈现稳定的服役信息反馈；当发生泄漏时，压力值开始下降，经历较短压力下降时间之后趋于动态平稳演变；显而易见的是漏点面积越大，相应的压力下降幅度也越大。

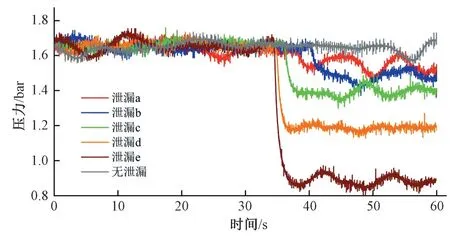
图6 管道不同状况下的采集信号Fig.6 Signals collected under different conditions of the pipeline

2.1.2 数据集扩充

采集到的原始管道压力信号是一维时间序列信号，泄漏特征出现在其某一段时间内。实现深度学习算法对管道泄漏检测需要大量的训练样本，且泄漏特征所在位置具有多样性。因此，本文采用平移的方式截取信号，其示意图如图7所示。在一组原始信号中截取多个样本，且各样本泄漏出现时刻各不相同，实现对训练数据的扩容以及涵盖了样本多样性。

图7 样本扩充示意图Fig.7 Schematic representation of the expanded sample

由于样本长度过短会导致无法从中提取充分地泄漏信息，同时样本长度过长又会加大计算量和计算时间，综合考虑下，本文选择的样本截取长度为30 000 个点，并在每一组已采集的原始信号上共平移截取10次，平移长度为1 500个点，数据集的样本容量能够扩充至2 000组信号，平移截取的部分样本如图8所示。同一原始信号上截取到的不同样本在时序上发生了变化，泄漏特征出现的对应时间各不相同。

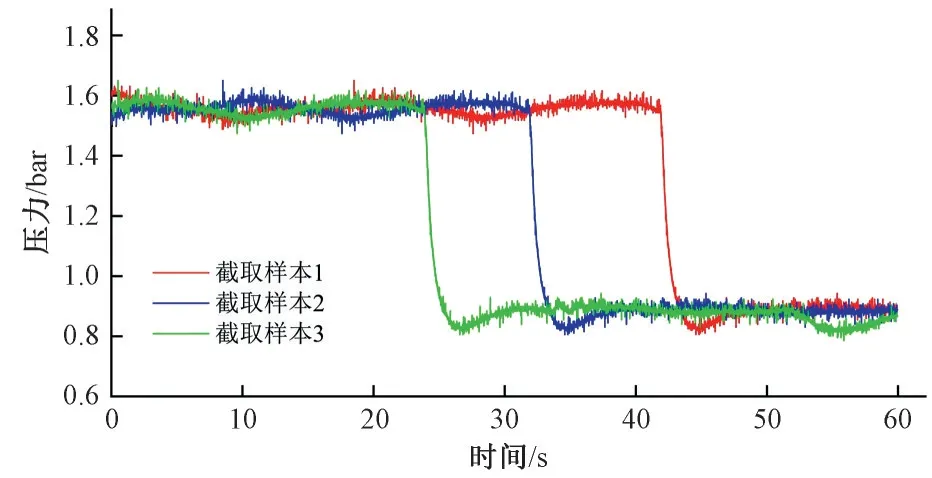
图8 平移截取部分样本Fig.8 Samples intercepted in panning

2.1.3 去噪处理

由于外部环境的干扰因素存在，原始压力信号中存有大量的噪声，这些噪声很可能会掩盖信号中的泄漏特征。变分模态分解［19］（Variational Mode Decomposition，VMD）是一种性能优良的去噪算法，能将原始信号分解为一系列本征模态函数（Instrinsic Mode Function，IMF），并不断迭代更新每个分量的中心频率和频段带宽，分离原始信号的自适应频率成分，提取包含管道内压力特征的频率分量。VMD 可以有效地克服模态混叠问题，有着很好的鲁棒性，因此本文采用该方法对信号进行降噪处理，将采集到的原始信号分解为5 个IMF 分量，剔除掉4个包含较多噪声的高频IMF 分量，实现对信号的去噪，其效果如图9 所示，去噪后的信号演变曲线密集的峰刺特征消失并逐渐变得平滑。去噪后的数据将被作为1D-CNN-LSTM 网络的输入。

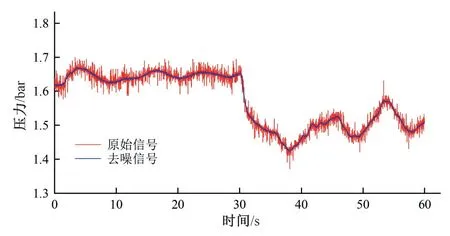
图9 去噪效果图Fig.9 Demonstration of denoising effect

2.2 模型参数与检测结果分析

在本文网络的训练过程中，初始学习率设置为0.001，且每经过三轮训练后学习率减半，该操作能使模型在前期训练较快，且后期波动性被明显抑制，从而更加容易接近最优解；采用了shuffle batch 方法打乱样本，增加随机性，可以提高网络泛化能力，避免过拟合；训练执行环境为CPU，Batch-size 为200；经过多次训练，最终得到最优网络的各项主要参数如表1所示。

表1 神经网络参数Tab.1 Neural network parameters

该最优网络的训练过程如图10 所示。图10 中蓝色曲线是训练准确率的变化过程，红色曲线是网络损失值的变化过程。由图10 所知，随着训练的推进，训练集准确率在大体上不断上升，反之网络损失值也在不断下降伴随着小幅演变振荡。当迭代次数达到60 次后，训练集准确率与损失值的变化都趋于平稳。直到迭代124 次后找到了最优结果。本次训练结果中，训练集准确率为100%，损失值为0.008 6，表明本网络的训练结果较好并将之保存。为证明网络的实际检测效果，将测试集带入本网络，得到测试集准确率为99.75%，说明本网络结构对管道泄漏有着良好的检测效果。

图10 准确率与损失的变化曲线Fig.10 Accuracy and loss variation curves

2.3 对比实验

在研究过程中发现，设置不同的网络层数，会对训练耗时和结果造成影响。理论上，网络层数越多，能够学习到更复杂的特征，损失值越小，检测准确率越高；同时，网络的复杂度也会相应增加，训练更加困难，效果不理想。

为验证本文所选模型对管道泄漏检测的有效性，同时考虑到通常CNN 网络的层数会设置三层及以上，本文设计了四种不同层次的1D-CNN-LSTM 网络结构以及1D-CNN 和LSTM 网络，在相同数据集的情况下，用其他神经网络和本文所用网络对比，为了避免偶然因素对网络的影响，每种网络的统计数据为3 次实验结果的平均值。各网络的训练过程如图11 所示，结果如表2所示，此外，测试集中各网络对于不同位置与不同开度的泄漏及无泄漏情况下的具体检测准确度如表3所示。其他网络结构如下：

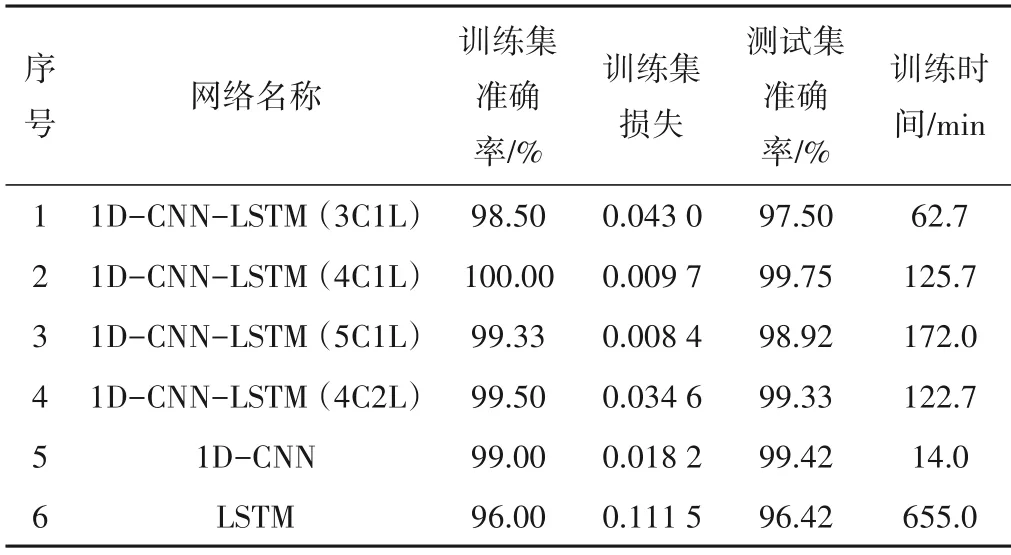
表2 不同网络结构的训练结果对比Tab.2 Comparison of training results for different network structures

表3 各网络对于不同情况的检测准确度Tab.3 Detection accuracy of each network for different situations

图11 不同网络结构的准确率与损失变化曲线Fig.11 Accuracy and loss variation curves for different network structures

（1）1D-CNN-LSTM（3C1L）：与本文结构相比，只保留前三个卷积组，LSTM层数为1。

（2）1D-CNN-LSTM（4C1L）：本文所用的网络模型。

（3）1D-CNN-LSTM（5C1L）：在本文所用结构基础上，再多加一层卷积层和池化层，其卷积核尺寸不变，深度为32，池化层与前层保持一样。

（4）1D-CNN-LSTM（4C2L）：与本文结构相比，多加了一层LSTM层，隐藏节点也为64。

（5）1D-CNN：只保留本文结构中的1D-CNN 部分，去掉LSTM 层，卷积层和池化层数目为4，其他参数与本文所用参数相同。

（6）LSTM：与本文所用结构相比，没有1D-CNN 部分，只使用单层LSTM层，隐藏节点数为64。

1～4 号网络是不同层次结构的1D-CNN-LSTM 网络，它们的对比实验探究了网络层次与训练结果的关系，其中，1号网络相比本文网络少了一层卷积层和池化层，在网络结构调试时发现，1 号网络由于网络深度较浅，对特征提取的能力不足，损失下降效果不好，有欠拟合的可能，损失值为0.043 0，在4 组网络中是最高的，相应的测试集准确率为97.50%，在4 组网络中最低。2 号网络是本文所用的网络结构，其网络拟合度以及泛化效果最优。3号网络在本文所用网络结构上多加了一层卷积层和池化层，随着网络深度的增加，网络复杂度也相应增加，训练损失虽比2号网络稍低，但训练耗时更长，且测试集准确率不是很理想，泛化效果不佳。4号网络在本文所用网络的基础上，增加了一层LSTM 层，与2 号网络相比，训练损失和测试集准确率都在下降，原因是网络深度的增加导致了过拟合。

将5 号和6 号网络与本文所用网络作对比，是为了探究本文所用网络将CNN 和LSTM 结合所带来的优势。相比之下，本文所用网络的训练准确率和损失都是最优的，原因在于1DCNN 和LSTM 网络分别只对局部空间特征和时序特征的敏感度高，训练过程中收敛较困难，在较长时间之后准确率和损失都有在一定范围的波动，收敛效果并不理想，所以训练结果稍差。而本文所用网络针对管道泄漏数据的局部空间特征和时序特征，建立的1D-CNN-LSTM 神经网络结合了CNN 和LSTM 的优点，可以充分提取时域压力信号中的泄漏特征，使网络的训练结果最优。

除此之外，在表3 中对比了各网络在各具体情况下的检测准确度，结果表明，当相对位置不同时，同一网络的泄漏检测准确度无明显差异；而泄漏大小不同时，对于较大泄漏，各个网络的检测准确率都较高，但开度a 与开度b 所对应的小泄漏，各个网络对其进行检测的准确率有较大差异，而本文所用网络对较小泄漏的检测也有很高的准确率，相较于其他网络为最优。