基于可拓神经网络的排涝泵站主机组动力特性大数据修正方法

2022-01-24杨玉泉张仁贡

中国农村水利水电 2022年1期

杨玉泉，张仁贡

（1.浙江同济科技职业学院，杭州 311231；2.浙江禹贡信息科技有限公司，杭州 310009；3.浙江工业大学，杭州 310014）

0 引言

为减少城市及工矿洪涝灾害改善水环境，许多城市、矿山都建设了排涝泵站。随着泵站综合效益日益提高，泵站主机组常年在配水调度需求下运行。主机组是泵站运行安全的重要设备，成为泵站长期稳定运行关键要素。泵站经多年运行，受自然和人为因素作用（制造、安装、运行管理等），泵站主机组设备常会出现振动、噪声以及机组故障问题。一个泵站若有多台机组，还涉及机组的优化组合、机组负载均衡以及机组损耗等问题［1］。上述问题的解决都涉及泵站主机组的动力特性研究。但是如何获取精确的泵站主机组动力特性是一个世界性难题，主要原因有：①我国大部分水泵建设时未考虑安装在线监测仪表，当泵站主机组安装完成后，无环境条件再加装在线监测仪表。②泵站主机组动力特性的主要参数中包含功率、扬程和流量，流量监测本身难度较大，尤其是流量的在线监测。③泵站主机组动力特性需要在不同扬程条件下的流量数值，其特性是一个曲面，但为了简化问题的分析，一般依据实际情况选取多个典型扬程，功率从0 到额定功率的条件下，获取流量数值，形成典型扬程下的动力特性方程。水工模型试验是解决复杂水力学问题的有效手段，所得到的试验结果真实可信。为此，需要做水泵主机组的真机试验，泵站要在维修工况下安装试验仪器，成本高，测量时间长，对整个泵站的运行产生较大影响。综上所述，寻找一种既可靠安全、又能够较高精度获取泵站主机组动力特性的方法具有较高的研究价值和较为广阔的实用前景。

一般在泵站主机组制造时，先做泵机模型，再对该模型进行模拟试验得到模型运转综合特性曲线，以指导泵站主机组的制造和安装，并作为第一手厂家试验资料提供给泵站主机组使用单位。从泵站主机组模型运转综合特性曲线获得的泵站主机组动力特性在教科书上有一定的介绍，本文简称为泵站主机组模型动力特性，该动力特性精度很低，往往与真机动力特性存在很大差距。随着自动化技术和物联网技术的发展，泵站运行基本上都采用自动化，利用物联网感知技术［2］，将泵站主机组的运行数据存储在云数据库中，多年运行积累形成了大数据［3］。但如何利用运行存储的大数据，来不断修正泵站主机组模型动力特性，使之不断自学习接近泵站主机组真机动力特性［4］，目前，国内外尚没有相关文献刊载该研究。

为此，笔者依托国家自然基金项目“流程化工业生产过程中的不确定动态调度方法及其应用（60874074）”、浙江省教育厅科研项目“基于大数据的杭州七堡排涝泵站运行优化研究”（Y201942901）和浙江省水利厅课题“泵站机组异常振动和温升研究——以七堡排涝泵站为例”（RC1981）的研究，通过泵站主机组模型运转综合特性曲线获得泵站主机组模型动力特性，利用大数据技术，结合可拓神经网络方法的动态修正和逼近，以获取排涝泵站主机组真机动力特性，并将该方法编译为计算机动态链接库（DLL），开发了“七堡泵站大数据仓库管理信息系统V1.0”（国家软件著作权登记号：2018R11L1440166），为下一步开展泵站的主机组振动原因分析、机组优化组合以及负荷优化调度奠定基础［5］。

1 关于模型动力特性方程

泵站主机组厂家提供给用户单位的模型综合运行特性曲线和获得的主机组模型动力特性曲线如图1 所示。功率流量（扬程）特性是主机组模型动力特性的主要特性，以下就以该动力特性为例进行研究。

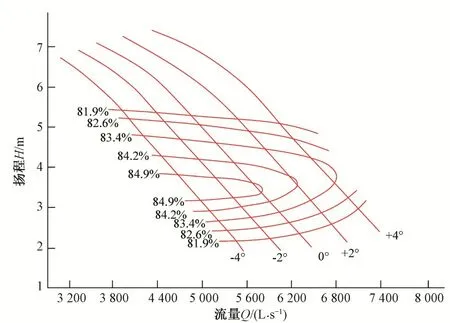
图1 水泵运转综合特性曲线Fig.1 Operation synthesized characteristic curves of hydraulic turbine

教科书中已有将水泵运转综合特性曲线获取功率流量（扬程）特性离散数据的步骤，本文不再累述。离散数据通过最小二乘法进行拟合为样条三次曲线方程［6］，在计算机语言求解中主要采用高斯函数和牛顿替代法［7］，技术应用常见于文献。所获得的方程在界面中绘制，即为图1。

2 三次指数矩阵数据处理方法

采用水泵运转综合特性曲线获取的水泵主机组模型动力特性对于正在运行的真机而言，精确的是很不够的。模型机经过放大制造、安装和长期运行，变化比较大。特别是对于大流量等非标准水泵，需要定制生产。故水泵主机组模型动力特性尚不能用于指导水泵的运行［8］。为此，笔者通过计算机监控系统的历史数据库以及云端运行管理数据库抽取实际数据，对水泵主机组模型动力特性方程进行修正，以提高动力特性精度。水泵主机组的扬程、功率、流量及效率的计算公式为：

式中：Qj为水泵主机的出口流量，m3∕s；Pj为水泵输入功率，kW；Hj为扬程，m；ηj为水泵的运行效率；j为水泵主机组的编号。

假设在历史数据库或云端运行管理数据库的大数据中抽取到一组数据，如某主机组的流量Qi和功率Pi，采用三次多项式拟合方程［9］表示为：

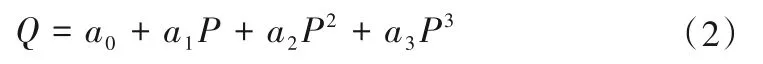
而依据模型动力特性方程获得流量为：

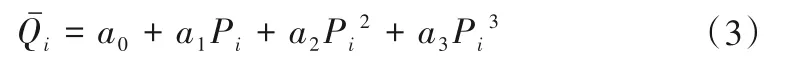
则它们的误差为：

两边平方可得：

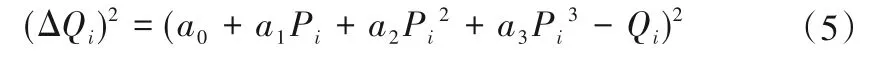
若有在历史数据库或云端运行管理数据库的大数据中抽取到n组数据，其总误差平方和为：

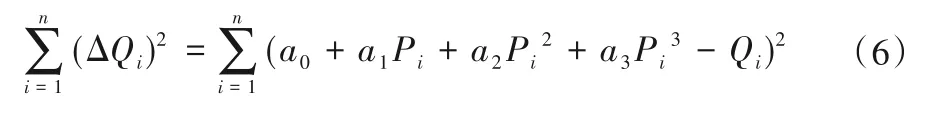
根据最小二乘法原理，当式（6）关于待定系数a0，a1，a2，a3的偏导数为零时，总的误差平方和取到最小值。并采用指数矩阵表示可得：

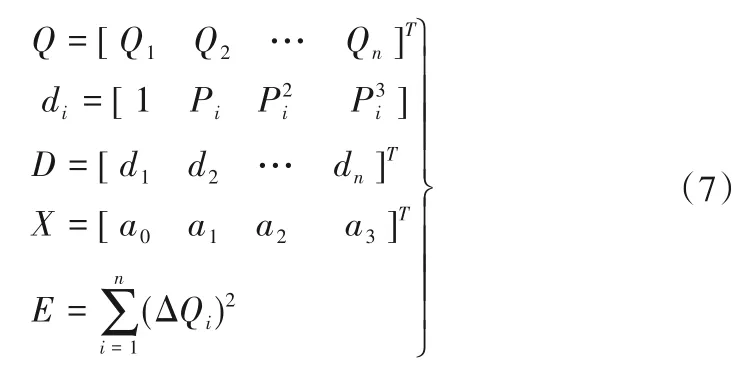
式中：Q为主机组的出口流量矩阵；di为主机组的功率矩阵；D表示功率转置矩阵；E 为总误差平方和；X 为系数矩阵。于是E 可表示为：

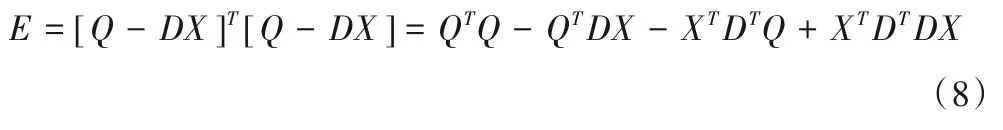
其中：

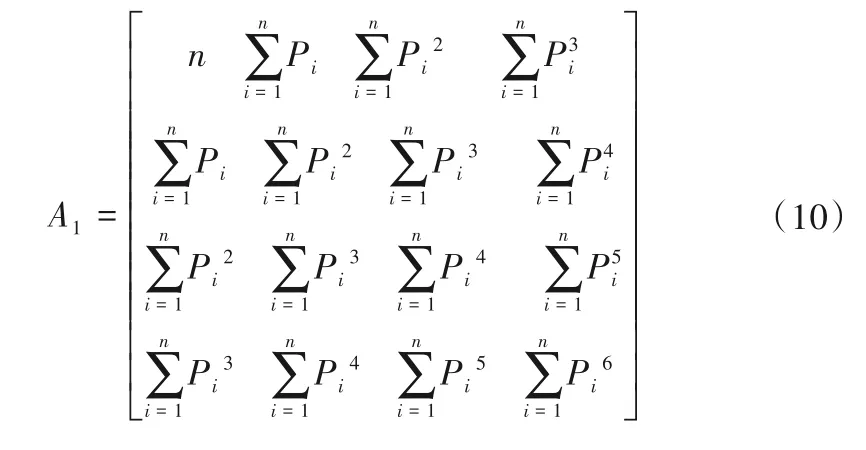
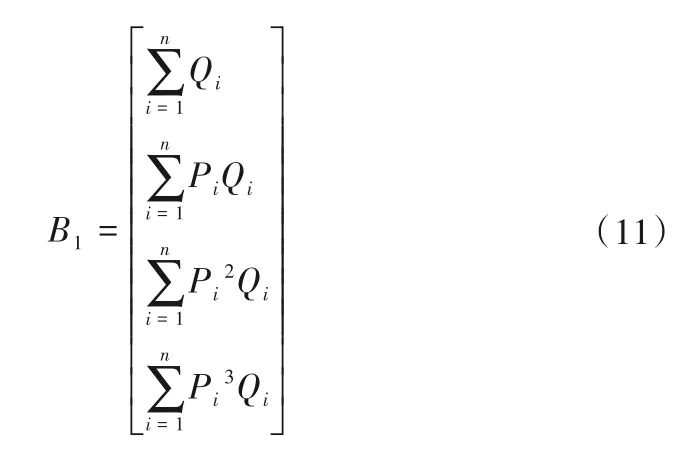
依据指数矩阵计算方法，原数据和新数据是一个叠加关系，对于大数据中抽取所得的一对流量数据Q和功率数据P，计算可得：

对于原数据引入衰减因子α（0 ＜α ＜1，可取α＝0.95），并与新数据合并可得：

于是，对于大数据中抽取所得的新数据流量Q和功率P，通过以上方法重新拟合新的功率流量（扬程）动力特性方程。

由于泵站主机组的动力特性方程在不同扬程或上下游水位下，具有相同趋势且不相交的特点（同趋不相交），研究表明所得曲线方程依据扬程的不同，具有线性等间距的特性（扬程等间距）［10］。由上述的三次指数矩阵数据处理方法可知，该方法是一种静态的以点替代点从而带动整个曲线进行修正的处理方法。该方法的缺点在于：①无法保证动力特性的“同趋不相交”和“扬程等间距”；②仅仅从历史数据库中抽取数据进行修正，无法从后续不断运行的数据中抽取数据而进行动态连续修正，使之不断逼近真机运行特性工况。为此，本文引入一种基于神经网络的动态可拓训练修正方法。

3 神经网络可拓训练方法

目前，随着大数据、云计算、5G、人工智能等技术的发展，神经网络（Artificial N euron Networks.ANN）［11，12］计算方法逐步得到流行，在使用该方法之前，需要将历史数据库云端化，并与云端运行管理数据合并为统一数据仓，本文称之为泵站云数据仓［13］。如何清洗、合并、存储、量化、归一等多数据仓库合并技术需要另外著文论述，本文不做介绍。神经网络方法将模拟人的大脑和神经元，将泵站云数据仓分为多个神经元节点，利用信息传输系统实现并行分布式处理，具有将数据进行快速分析、存储、计算、拟合和闭环循环，具有自学习和自适应能力，但神经网络方法的缺点在于比较适应于初始值为零或随机数据，对于抽取数据密集度过高，往往会陷入局部极值或死循环［14］。为此，笔者受到蔡文教授可拓理论（extension theory）［15］和赵燕伟教授的《可拓设计》［16］等启发，引入了可拓理论中的元理论，有效地解决了神经网络方法的上述缺点。

泵站云数据仓中将不断产生新的数据，一旦数据触发了规定的阀值，即可作为初始值输入神经网络系统进行计算，为了避免陷入局部极值或死循环，在定义阀值时引入可拓元理论，即计算旧数据与获取的新数据的可拓距，当可拓距满足条件时再进入神经网络系统进行计算，可拓距可以变换为阀值使用［17］。本研究利用可拓物元模型确定初始权值，可拓距的计算采用下式：

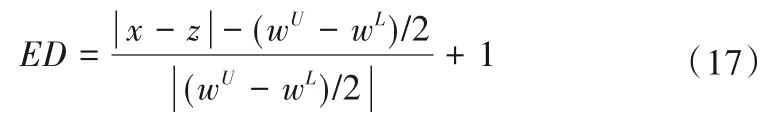
式中：ED为可拓距；[wU，wL]为可拓物元区间；x为可拓区间外待测对象即泵站主机组（或具体的流量、功率、扬程等工况）。

ED 用来判别待测对象x和一个可拓物元区间[wU，wL]的可拓距。由于在泵站云数据仓中存在海量数据，同时存在多个分类或聚类数据，例如振动区间、气蚀区域、磨损趋向等聚类，为了辨识多个分类或聚类数据并与神经网络的并列分布计算方法相适应，采用一种双向并列的链接结构［18］，融入到神经网络计算方法中，不妨称该算法结构为可拓神经网络双向并列链接结构，图2所示。

图2 可拓神经网络双向链接拓扑结构Fig.2 Topological structure diagram of extension neural network with bidirectional links

由于采用泵站云数据仓的可拓距过滤式阀值数据采纳方法，所用的神经网络方法是一种具有自适应的非监督学习算法，而可拓神经网络双向并列链接结构有效改进了神经网络的非监督学习算法，利用可拓距ED 度量聚类中心、符合目标的边界数值和初始权值。

具体方法为：①当可拓距ED 度量通过时，获取对应初始权值的样本，作为第一个样本，称之为原始样本。②在符合目标的边界数值的条件下，采用神经网络方法计算原始样本，每次传到至下一个神经元时，采用可拓距ED 度量聚类中心，避免陷入局部极值或死循环，直到获得计算最优结果，作为第二个样本。③第一个样本和第二个样本进行可拓距ED 度量，记录比较后符合条件的样本。④不断并行和循环计算该过程，直到所有样本数据计算完成，进入稳定的分类和聚类集合，更新替换原来数据样本集合。若将可拓距ED 度量转换为对应参数如流量、功率、扬程等数据阈值时，可以设置样本特征的总个数。由于根据可拓距原理，当一个数据点落在可拓区间内时，则可拓距小于1。

因此，当泵站云数据仓获取n个特征数据，对于xi=｛xx1，xx2，…，xxn｝，则当EDp=min{EDm}＞n，则说明了xi不属于聚类p，需要创建一个新的样本聚类。如果EDp＜n，则样本xi属于聚类p，对于聚类p 所对应的样本需要进行调整或替换，主要动态修正样本的权值和聚类中心点，如式（18）～（21）。

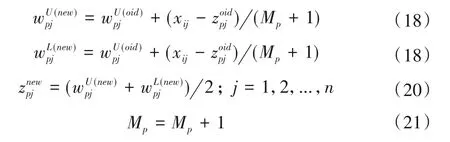
式中：Mp是为修正后聚类p的新样本个数。

如果输入第i 个新样本的数据物元xi从原聚类O 变换到新聚类k，则修正后调整聚类O 所相对应的权值和聚类中心点，如式（22）～（25）所示。

综上所述，本研究所提出的神经网络可拓训练方法，将可拓元理论及计算方法融入到神经网络非监督学习算法中，经过实验比较可知，其训练时间平均可提升50%，且容易获取数据库的数据或知识［19］。同时，优化了神经网络算法，避免局部收敛，具有稳定性和可塑性等特点。值得注意的是，要保持神经网络的良好优化计算效果，可拓距的选取非常重要，可拓距与阈值距离参数紧密关联，这就使得阈值距离参数的选取至关重要，因此需要进行不断试验研究和较长时间的观察积累，进行调整才能结合实际数据实时修正训练的需要。

4 实例分析

杭州市某排涝泵站位于江干区和睦港出江口，主要承担上塘河流域防洪排涝，兼顾上塘河流域的环境景观配水。共布置7台10 kV直接启动的高压潜水轴流泵，1～4号泵采用1400QZ-130 型，5～7 号泵采用1600QZB-125 型。由于制造、安装或运行工况偏差（泵站受钱塘江潮位影响，其扬程变化频繁，变化幅度大）等原因，5 号泵运行状态不稳定，振动较大，噪音偏高，故障率较高，对整个泵站的安全和优化运行及调度产生较为明显影响。因此本文取5 号泵为例进行研究，5 号泵设计流量12 m3∕s，设计扬程3.5～6.0 m，转速295 r∕min，电机功率800 kW，叶轮直径1.54 m，设计运行效率81.3%～84.3%。

依据5 号泵厂家提供的泵主机组模型运转综合特性曲线，获取模型动力特性数据，然后采用最小二乘法进行拟合，拟合后的方程组如式（26），流量功率动力特性曲线如图3（a）所示。

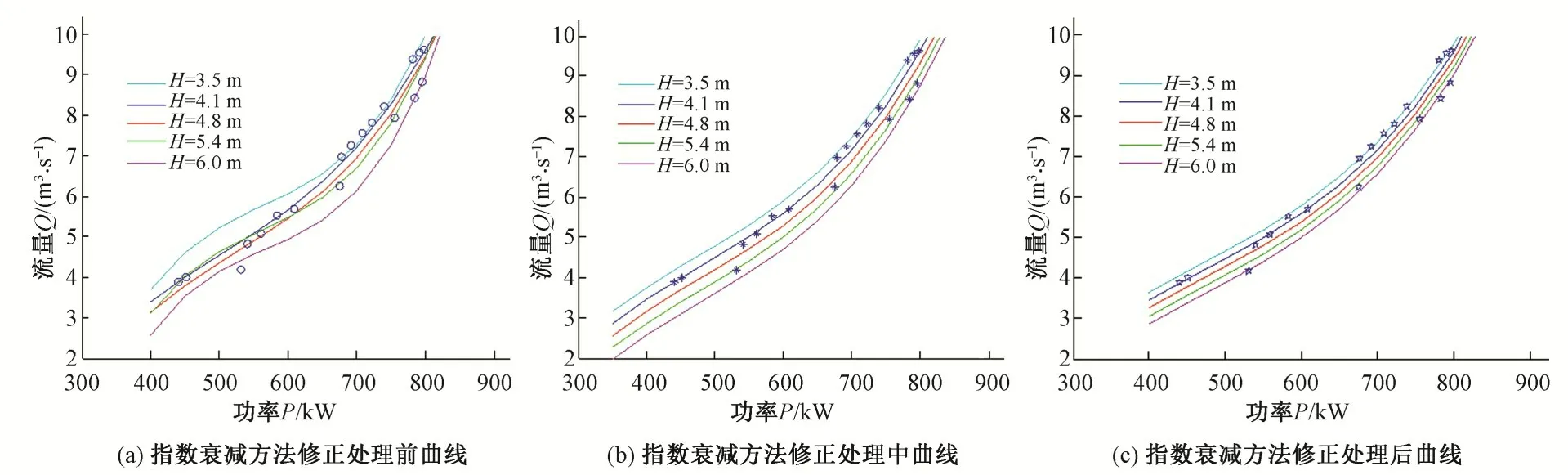
图3 指数衰减方法修正处理前后曲线Fig.3 Before and after comparisons fixed by Exponential decay method

从图3（a）可知，在设计扬程3.5～6.0 m 之间，除了3.5和6.0最小和最大扬程外，另取4.1、4.8、5.4 作为典型主机组扬程，从模型运转综合特性曲线获取的离散数据拟合的流量功率动力特性曲线方程，绘制后可见其趋势和间隔都不均匀，且各个典型扬程特性的曲线有明显的相交现象，不符合实际要求，尤其是当扬程为H=3.5 m时，失真特别厉害。

从该泵站云数据仓由计算机监控系统历史数据库［20］和泵站标准化运行管理数据库云化合并而成［21，22］，从云数据仓中挖掘3.5、4.1、4.8、5.4、6.0 m 等典型泵机扬程的真机运行数据进行基于三次多项式指数矩阵处理方法的修正，取矩阵修正系数α＝0.95，修正替代后重新最小二乘法三次多项式拟合后其特性方程如式（26），绘制的曲线如图3（b）所示。从图3（b）可知，修正后的方程其曲线有比较明显的改变，但是3 个典型扬程下的特性曲线虽然不再交叉，但是依然存不等距现象，不符合泵站主机组流量功率动力特性“扬程等间距”的要求。这也是上文所提到的基于三次多项式指数矩阵处理方法的缺陷，因此需要采用可拓神经网络方法进行进一步动态数据训练和修正。

按照“同趋不相交”和“扬程等间距”的流量功率动力特性的要求，将3.5、4.1、4.8、5.4、6.0 m 扬程作为泵站数据仓触发器［23］，激发实时获取后续运行样本，采用可拓神经网络方法进行动态训练和修正，经过一年多时间的训练运行，获得各数据样本98 个，符合可拓距的样本62 个，选择符合聚类可更新数据样本54个进行列表，如表1所示。

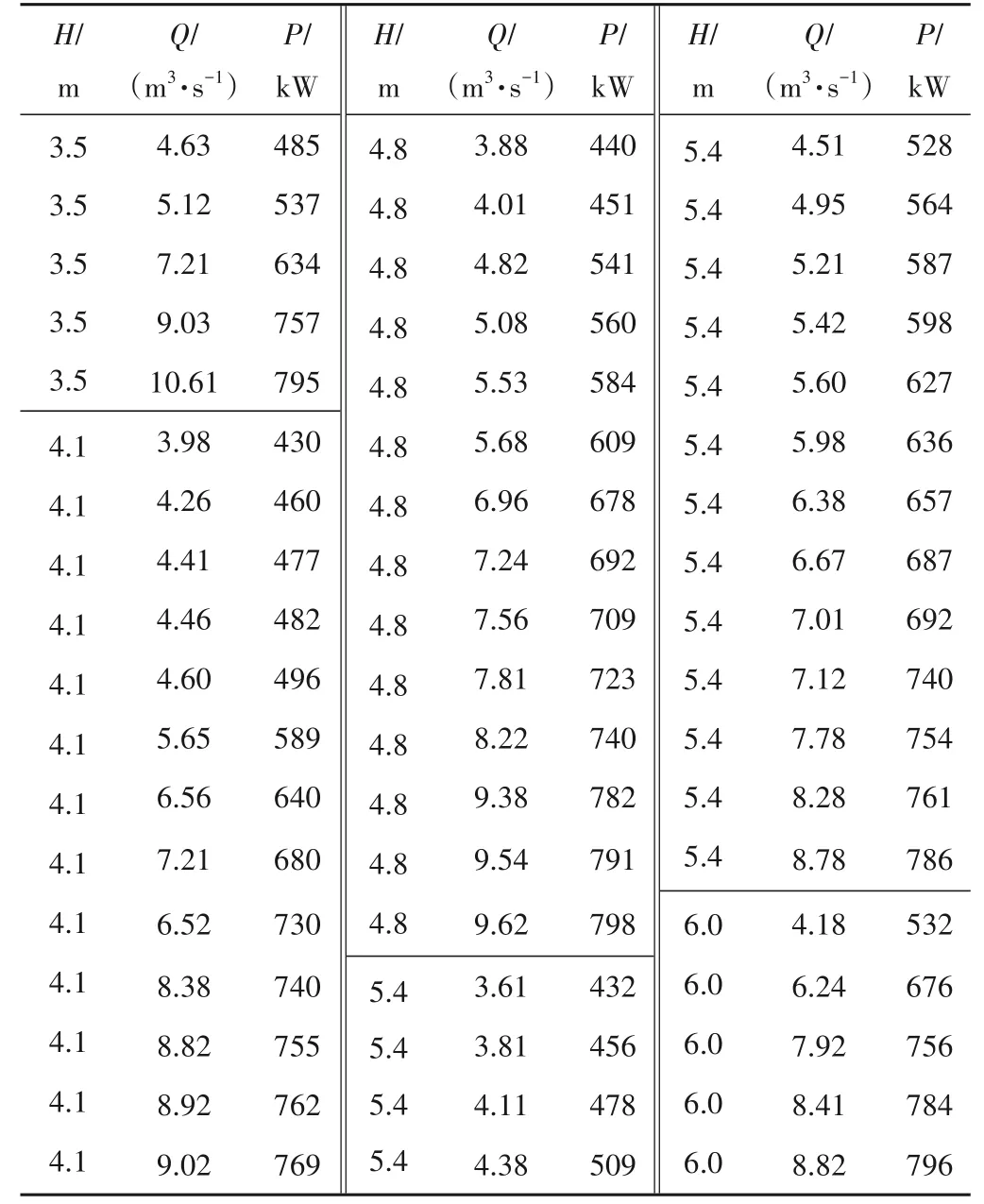
表1 各典型扬程下的流量功率聚类更新数据样本Tab.1 Cluster updating data samples of traffic and power under each typical head

可拓距调整每月进行一次，最后经过12 次调整，可拓距阈值距离参数设置如下：｛H ≡3.5｝∈[0.02，0.26]、｛H ≡4.1｝∈[0.27，0.46]、｛H ≡4.8｝ ∈[0.47，0.65]、｛H ≡5.4｝∈[0.66，0.86]、｛H = 6.0｝∈[0.87，0.98]。

经过54个数据样本的可拓神经网络实时训练修订后，重新拟合的方程如式（28），特性曲线如图3（c）。

从图3（c）可知，泵站主机组流量功率动力特性基本符合“同趋不相交”和“扬程等间距”的要求，符合实际情况。表1 中的数据样本比较集中在中高功率段，且最低扬程和最高扬程两个典型扬程的数据样本偏少，这与实际运行的工况密集度有关。随着时间的推移，样本数量越来越多的情况下，特性曲线方程也必将越来越符合泵站主机组的实际运行工况，越来越能指导实际运行调度与决策［24，25］。

采用C++语言将可拓神经网络方法编译形成DLL动态链接库文件，嵌入到七堡泵站大数据仓库管理信息系统中，计算结果可以通过客户端软件泵站主机组动力特性分析系统进行展示，系统主界面如图4。