考虑需求响应和储能寿命约束的多类型电源协同调度

2022-01-23李琳玮宁光涛陈明帆梁亚峰何礼鹏陈皓勇郑晓东

浙江电力 2021年12期

李琳玮，宁光涛，陈明帆，梁亚峰，何礼鹏，陈皓勇，郑晓东

（1.海南电网有限责任公司，海口 570203；2.华南理工大学电力学院，广州 510640）

0 引言

随着能源危机和环境危机的不断加深，各国纷纷走上以开发清洁高效的新能源为主的绿色能源发展道路[1-2]。2020 年12 月，习总书记在国际气候雄心峰会上提出“碳达峰”“碳中和”的发展目标，我国正在大力发展以风电、光伏等可再生能源为主的低碳能源系统，高比例可再生能源并网将是未来电力系统的基本特征[3]。

风电出力具有一定的反调峰特性，当夜间风电出力较高时负荷处于低谷，而白天负荷水平较高时风电出力较小，这间接拉大了负荷峰谷差，增加了调峰压力，系统容易面临灵活性调节资源不足的局面。以火电机组为主的调峰机组常常需要频繁启停，容易造成火电机组在负荷低谷时负荷率不高的运行状况，降低系统运行效率[4]。

电化学储能具有较强的灵活调节能力，能够根据系统的实际运行需要进行快速充放电，这有助于改善火电机组频繁启停的运行状况。近年来，电化学储能发展较快，建设成本不断下降[5]。因此，在电网侧配置一定规模的电化学储能，能够起到削峰填谷、改善负荷曲线特性的作用。

同时，柔性负荷作为一种双向互动的灵活性资源，通过需求侧管理，可削峰填谷、平抑间歇性能源波动和提供辅助服务[6]。利用电化学储能的灵活调节能力和柔性负荷的快速响应能力，发挥源-荷-储联合调度作用，有利于丰富电网调度的调节手段。

文献[7]将柔性负荷分为可转移负荷、可平移负荷和可中断负荷3 类，同时建立考虑3 类柔性负荷的机组组合模型。文献[8]建立了计及可转移负荷、考虑火电机组和风电机组的日前调度方法。文献[9]在微电网运行优化中考虑可中断负荷，建立考虑联络线波动最小的微电网多目标优化运行模型。文献[10]考虑了实际运行中可能发生的随机故障，包括发电机组的停运、输电线路的故障以及可中断负荷的随机毁约，建立机会约束下的含可中断负荷的电力系统优化调度模型。文献[11]在光伏和储能的协调规划模型中考虑柔性负荷，其结果表明柔性负荷能够降低系统所需配置的储能容量，提高光伏消纳率。文献[12]建立考虑柔性负荷响应不确定性的多时间尺度协调调度模型。文献[13]针对新型智能小区，提出一种适用于负荷聚合商的可削减柔性负荷实时需求响应调度策略。文献[14]建立了以电动汽车退役电池为柔性负荷的电力系统风险调度模型。然而，以上所建立的模型存在2 个问题：在考虑电化学储能参与电网调度时，没有考虑到储能电池的放电深度对其寿命带来的影响，容易导致放电深度过高使得储能电池的实际寿命大大缩短；没有将储能与柔性负荷同时考虑在内，没有考虑电化学储能和需求响应的协同作用。

因此，本文建立考虑需求响应和储能寿命约束的多类型电源协同调度模型，同时考虑火电机组、风电机组、水电机组、核电机组，并且引入需求响应（包括可中断负荷和可转移负荷），以发挥电化学储能的灵活调节能力和柔性负荷的快速响应能力。最后，以某地区电网为例进行仿真分析，验证所建模型的有效性。

1 考虑电化学储能的多类型电源模型

本文结合火电、水电、风电、核电等多类型电源的运行特性，建立了考虑电化学储能的多类型电源模型。

1.1 火电机组的相关约束

式中：Pg，t为火电机组g 在第t 时段的出力；Pg，max和Pg，min分别为火电机组g 出力的最大值和最小值；分别为火电机组g 向上和向下爬坡速率的限值；Ig，t为火电机组是否运行的指示变量，Ig，t=1 表示火电机组g 在第t 时段处于运行状态；T 为1 个调度周期内的时段总数；分别为火电机组g 的最小开机时段数和最小关机时段数。

式（1）表示火电机组的出力约束，式（2）表示火电机组的爬坡速率约束，式（3）表示火电机组的最小开机时段数约束，式（4）表示火电机组的最小关机时段数约束。

1.2 风电机组的相关约束

式中：Pw，t为风电机组w 在第t 时段的出力；为风电机组w 在第t 时段的预测出力。

由于风电机组的出力具有随机性，在日前计划中按照风电机组的预测出力进行整定，即在考虑风电全额消纳的基础上，安排其他机组发电计划。

1.3 水电机组的相关约束

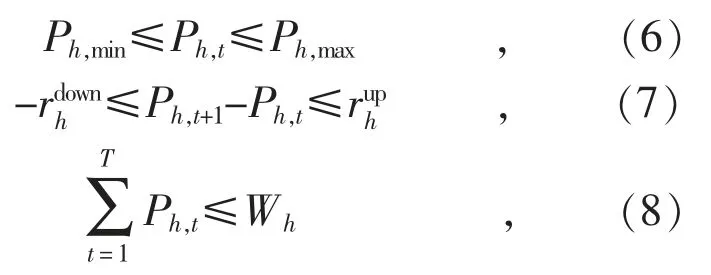
式中：Ph，t为水电机组h 在第t 时段的出力；Ph，max和Ph，min分别为水电机组h 出力的最大值和最小值；分别为水电机组h 向下和向上爬坡速率的限值；Wh为水电机组用于发电的最大水量（已转化为相应电量）。

式（6）表示水电机组的出力约束，式（7）表示水电机组的爬坡速率约束，式（8）表示水电机组用于发电的水量约束。

1.4 核电机组的相关约束

若核电机组参与调峰，频繁调节容易造成反应堆芯局部温度过高等安全问题，因此核电机组一般按照基荷状态设计运行。本次研究考虑核电机组的2 种工作状态[15]：满功率状态A 和低功率状态G。

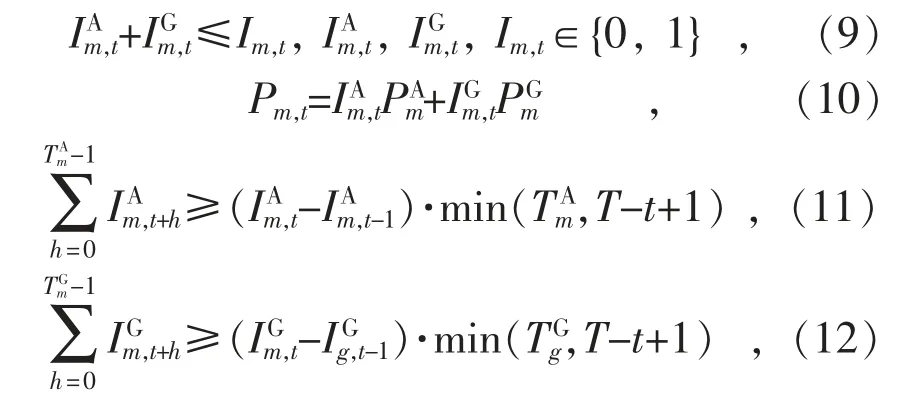
式中：Im，t为核电机组是否运行的指示变量，Im，t=1表示核电机组m 在第t 时段处于工作状态；和分别为核电机组m 运行在满功率状态A 和低功率状态G 的指示变量，取值为1 时表示核电机组处于该种运行状态；Pm，t为核电机组m 在第t时段的发电功率；分别为核电机组m 在满功率状态A 和低功率状态G 下的发电功率；和分别为核电机组m 在满功率状态A 和低功率状态G 下的最小运行时间。

式（9）表示核电机组只能运行在满功率和低功率的其中一种状态，式（10）表示核电机组的2种工作状态只能分别以固定功率运行，式（11）和（12）分别表示核电机组在满功率和低功率运行状态应该满足的最小运行时间约束。

1.5 功率平衡约束

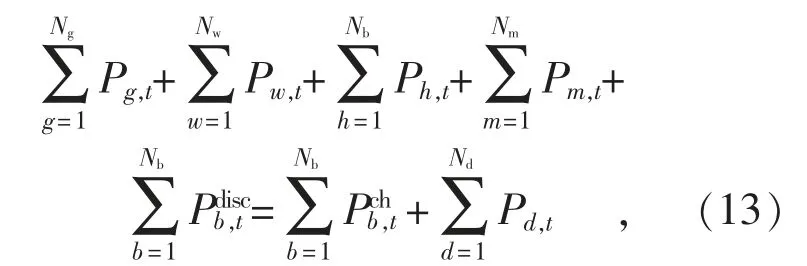
1.6 备用容量约束

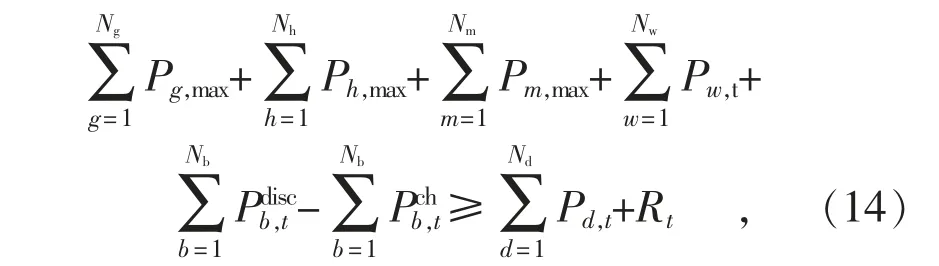
式中：Pm，max为核电机组m 的出力最大值；Rt为第t 时段系统的旋转备用容量。

1.7 线路潮流约束

式中：γgl，γwl，γhl，γbl，γdl分别为火电机组g、风电机组w、水电机组h、储能电池系统b、负荷d对输电线路l 的功率分布因子[16]；Pl，max为输电线路l 的传输功率上限值。

1.8 储能电池模型

在机组组合中考虑储能电池参与电网调度，有利于提升系统运行的灵活性，但储能电池的频繁充放电行为将大大降低储能电池的使用寿命。忽略储能电池的寿命约束将导致对调度方案的运行成本计算偏低。放电深度和日循环次数会对储能电池的使用寿命带来影响。因此储能电池的实际寿命Tcalendar由电池的浮充寿命Tfloat和循环寿命Tcycle中的较小值确定，即：

式中：浮充寿命Tfloat是出厂时的服务年限；循环寿命Tcycle反映了电池在达到寿命终点之前的充放电次数，是电池储能达到失效时的实际工作年限。

工程上常用雨流计数法确定电池储能的放电深度[17]。按照雨流计数法确定循环放电深度之后，电池的循环寿命可以拟合为：

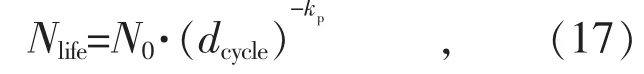
式中：Nlife为电池储能达到实际寿命时的循环次数；dcycle为电池储能每次充放电循环的放电深度；N0为电池储能以100%放电深度充放电时的循环次数；kp为拟合参数。通常电池厂家会提供相关参数。

由式（17）可知，储能电池每次充放电过程的放电深度越大，电池的循环寿命减少得越多。雨流计数法包括非凸的复杂计算，非线性程度较高，为了简化计算，本文采用基于充放电功率的寿命模型。基于充放电功率的寿命模型通过给储能电池每次的充放电功率分摊一定的折损成本，可以较为准确地刻画储能电池产生的运行成本。在调度计划中引入储能电池的折损成本可以限制储能电池的充放电深度和次数，避免电池由于过度充放电损耗太快而减少寿命。因此电池储能的折损成本Fb可以表示为：

储能电池的单位折损成本为：

式中：Lb，T为储能电池系统b 全寿命周期内的总充放电量；Cb，APV为储能电池系统b 投资和运行维护成本的年值；Tb，float为储能电池系统b 的浮充寿命。

储能电池投资和运维成本的年值：

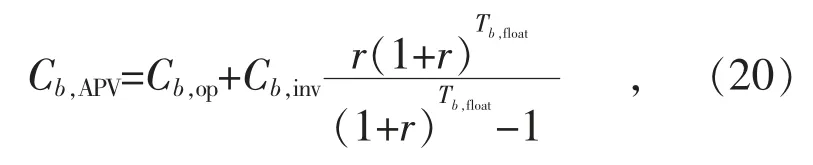
式中：Cb，inv为储能电池系统b 的投资成本，由单位投资成本乘以储能电池容量得到；Cb，op为储能电池系统b 的年运维成本；r 为贴现率。在本文中，N0取1 591，kp取2.09，Tfloat取10 年，r 取5%。

储能电池在运行过程中应该满足充放电功率上下限、荷电量上下限、相邻时段的荷电量耦合等约束条件：

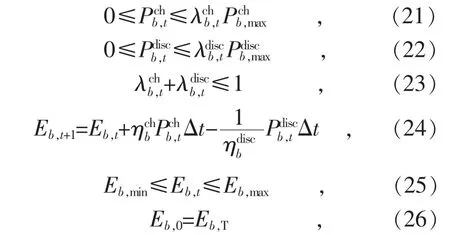
式（21）和式（22）分别表示储能电池的充放电功率约束，式（23）表示储能电池只能运行在充电和放电2 种状态，式（24）表示储能电池系统相邻时段荷电量的耦合约束，式（25）表示储能电池系统荷电量的上下限约束，式（26）保证储能电池系统调度周期始末的荷电量相等。

2 柔性负荷模型

面对不断提高的风电渗透率带来的调峰压力，柔性负荷和电化学储能的协同优化能够更好地提升系统的灵活调节能力。本文将系统中的负荷分为固定负荷和柔性负荷，其中柔性负荷还包括可转移负荷和可中断负荷。显然，用户d 在第t 时段的负荷Pd，t为：

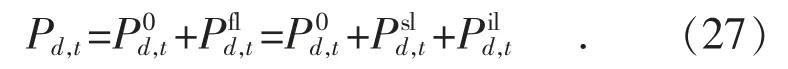
在系统的电力供应中，部分负荷的用电量不受电网调度控制，发电部门需要按照这部分负荷的出力曲线制定发电计划，本文称这部分负荷为固定负荷。

2.1 可中断负荷

按照电网与用户签订的合约，电网根据系统的实际运行要求，向签约用户下达电力中断的指令，同时给予用户一定的经济补偿，可中断负荷的实际负荷值与最大可中断次数、中断负荷量的关系为：

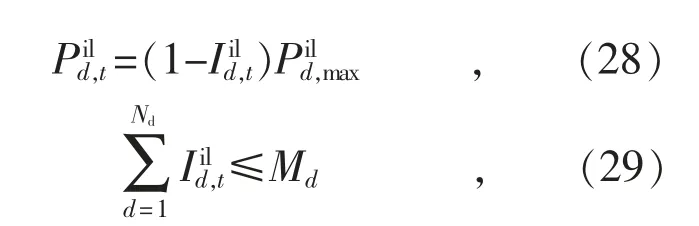
可中断负荷发生负荷中断可以获取一定的补偿费用Fil，可以表示为：

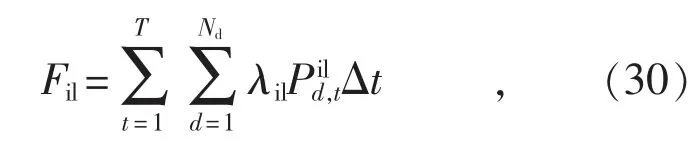
式中：λil为可中断负荷发生中断的单位补偿成本。

2.2 可转移负荷

可转移负荷的负荷特性灵活，可根据运行需要灵活调节各时段的用电量，在一个调度周期（如24 h）内保持总用电量不变，如电动汽车换电站、冰蓄冷以及工商业用户的部分负荷等[18]。

可转移负荷的补偿费用Fsl可以表示为：

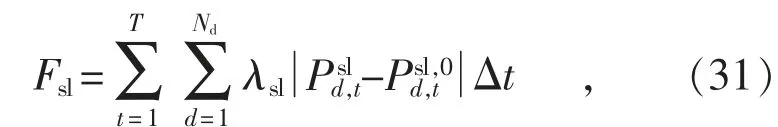
式中：λsl为可转移负荷的单位补偿成本；为用户d 在第t 时段调整前的可转移负荷。

式（31）为包含绝对值的表达式，一般没有办法直接求解，故引入辅助变量，式（31）转换为：

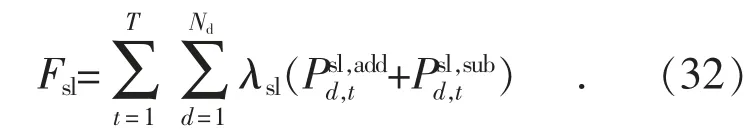
可转移负荷的相关约束为：

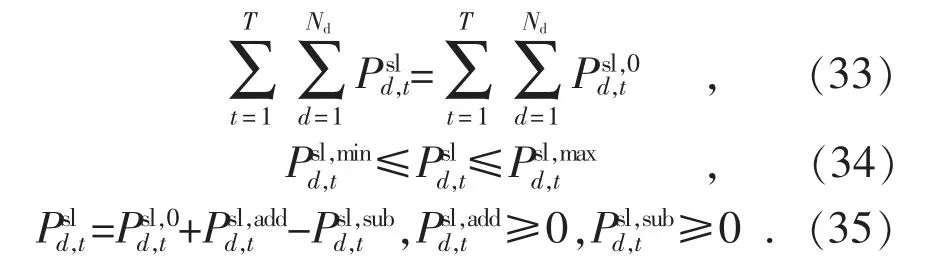
式（33）表示可转移负荷在调度周期内的总量保持不变，各时段的负荷可以在一定范围内进行调整。式（34）对调整后的各时段可转移负荷进行限制，本文取可转移负荷最小值，可转移负荷最大值。式（35）描述可转移负荷调整前后的关系。

3 考虑需求响应和储能寿命约束的多类型电源优化运行

考虑需求响应和储能寿命约束的多类型电源优化运行以系统在调度周期内的运行总成本最小为目标，同时考虑火电机组和核电机组发电所需的燃料费用、火电机组的开停机费用、柔性负荷的补偿费用和储能电池的折损成本。

系统的运行总费用F 可以表示为：

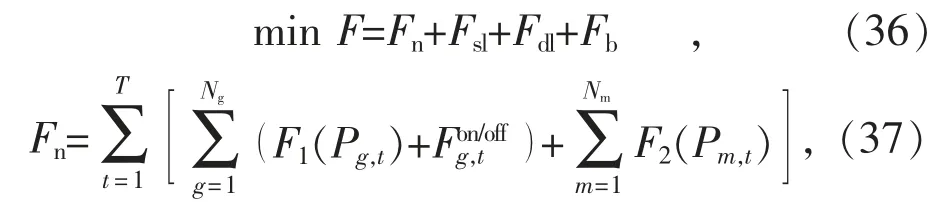
式（36）—（40）中：Fn为火电机组和核电机组的运行费用；F1（Pg，t）为火电机组的燃料费用；为火电机组的开停机费用；F2（Pm，t）为核电机组的燃料费用；ag，bg和cg分别为火电机组g 燃料费用与发电功率的二次函数关系式的二次项、一次项和常数项系数；bm和cm分别为核电机组m 燃料费用与发电功率的一次函数关系式的一次项和常数项系数；分别为火电机组g 的单次开机、停机费用。

表示火电机组燃料费用的二次函数可以通过分段线性化[19-20]的方法进行处理。假设火电机组的出力区间为[Pmin，Pmax]，用n+1 个点x0≤x1≤…≤xk≤…≤xn（其中x0=Pmin，xn=Pmax）将该区间等分为n 个小区间，如图1 所示。

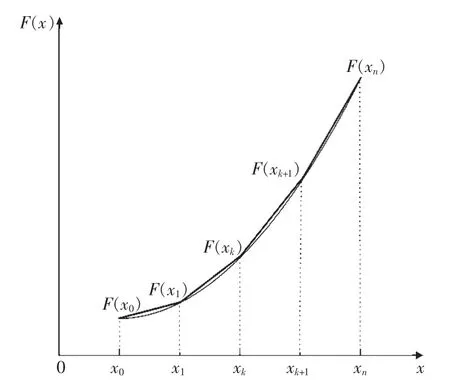
图1 燃料成本二次函数线性化示意图

对于每个小区间内的二次函数值可以用割线进行近似线性化：

式中：xk≤x≤xk+1。

采用数学规划软件GAMS 的SOS2 型变量可以将横坐标x 表示为：

式（43）只有2 个相邻的SOS2 型变量之和为1，其余变量为0。因此，通过SOS2 型变量可以识别出火电机组的出力位于哪个分段区间内，从而采用相应的割线进行线性计算。

4 算例仿真

4.1 算例描述

以某地区电网为例进行仿真分析。该地区共有9 台火电机组、3 台水电机组、5 台风电机组、2 台核电机组，各类电源的装机容量及占比见表1。系统风电渗透率达到25%，属于高渗透率可再生能源电力系统。火电机组和核电机组的基本参数见表2、表3。此外，在现有基础上加入3 套储能电池系统，储能电池系统的基本参数见表4。旋转备用设置为总负荷的10%。固定负荷占总负荷的90%，可转移负荷和可中断负荷分别占总负荷的5%，见表5。可转移负荷和可中断负荷的单位补偿费用分别为50 元/MWh 和400 元/MWh。本文所建模型本质上是一个混合整数规划问题，可以通过成熟的商用求解器进行求解。本文通过数学规划软件GAMS 调用CPLEX 求解器进行求解，运行环境为Core（TM）i5-8250U CPU 1.80 GHz，内存为8 GB。

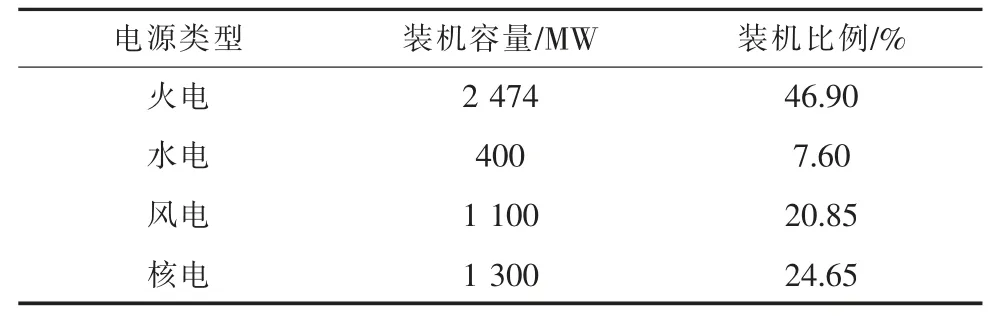
表1 系统各类电源的装机容量及比例

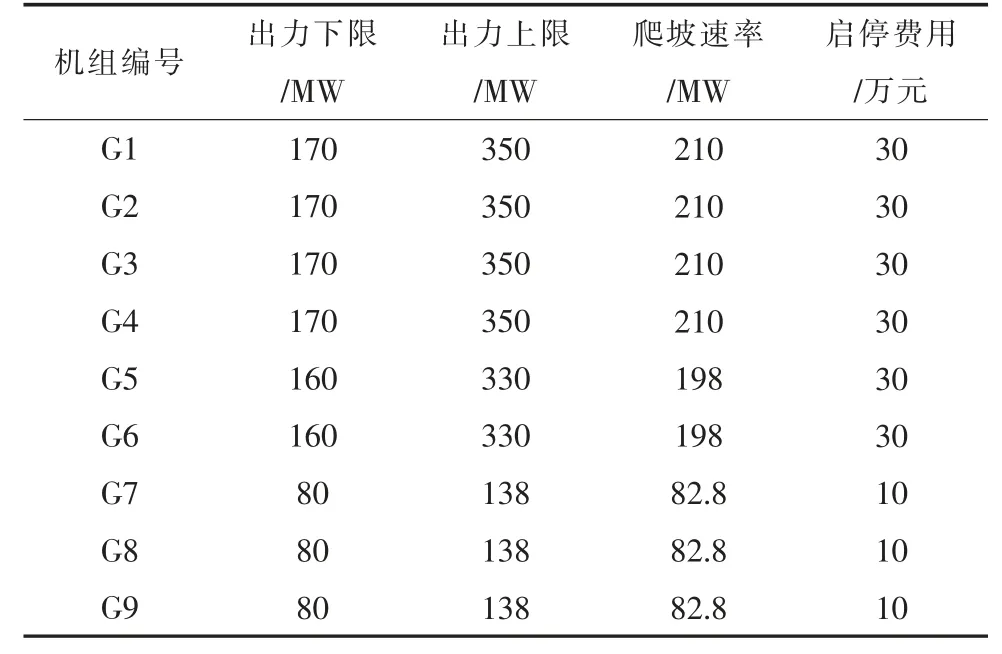
表2 火电机组的基本参数

表3 核电机组的基本参数

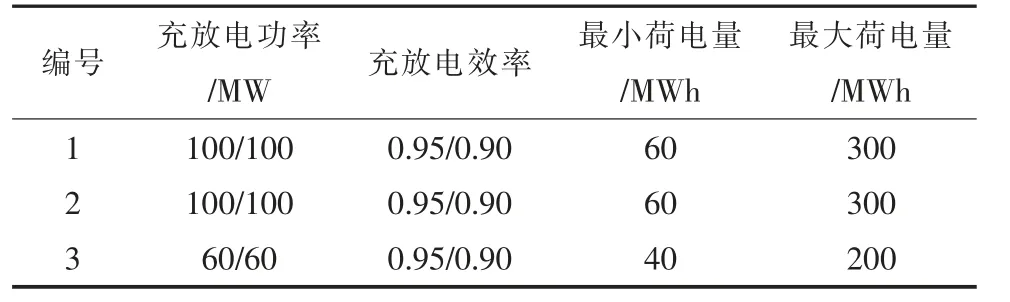
表4 储能电池系统的基本参数

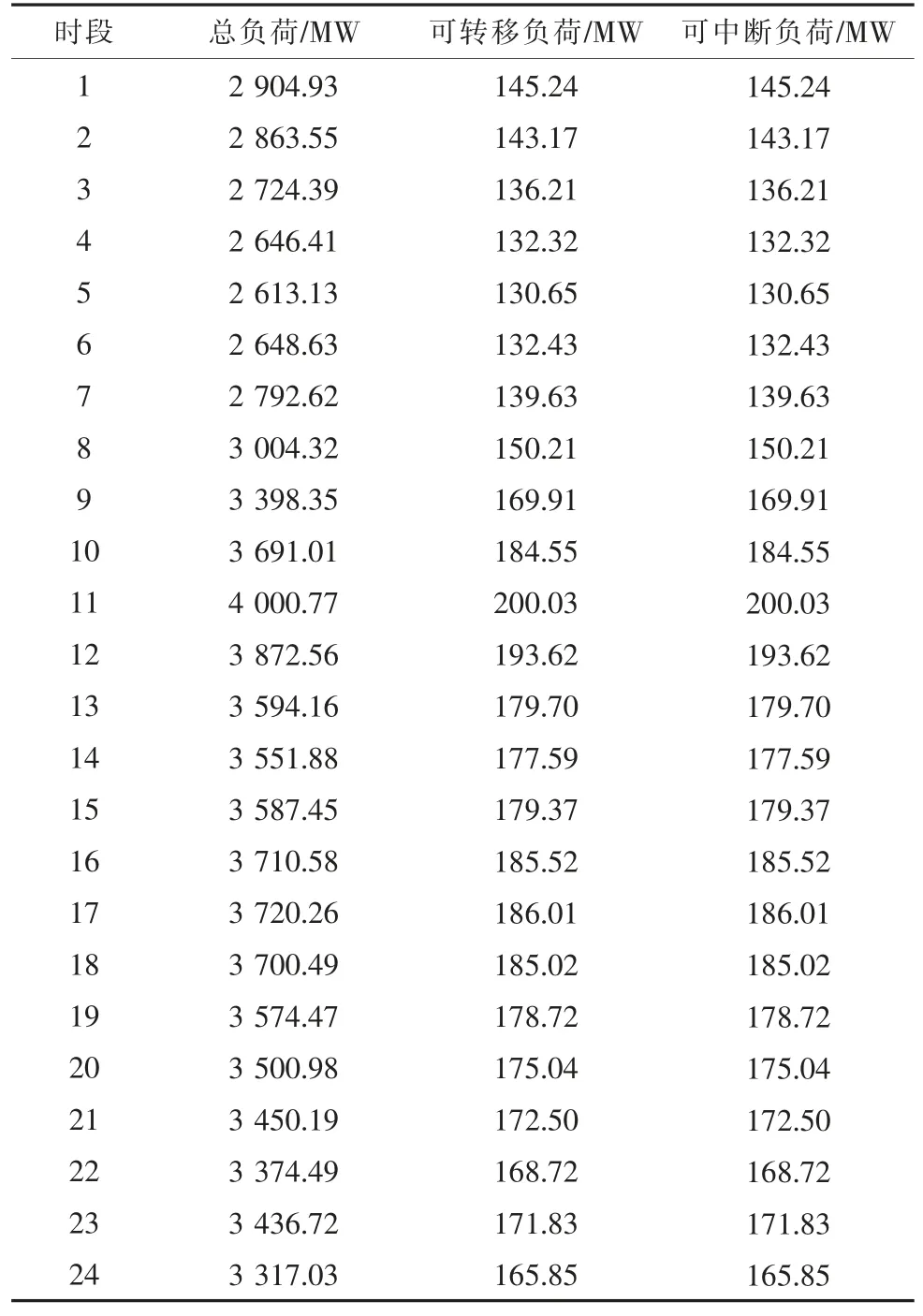
表5 系统各时段的总负荷和柔性负荷

4.2 4 种运行场景的优化对比

为了探究柔性负荷与储能电池协调运行对系统运行经济性的优化效用，下面分为4 种场景进行仿真计算：

场景1：系统没有储能电池和柔性负荷。

场景2：系统有储能电池，没有柔性负荷。

场景3：系统没有储能电池，只有柔性负荷。

场景4：系统既有储能电池，又有柔性负荷。

根据给定的各项参数和设置的运行场景进行仿真计算，得到不同场景下的系统运行经济性，如表6 所示。

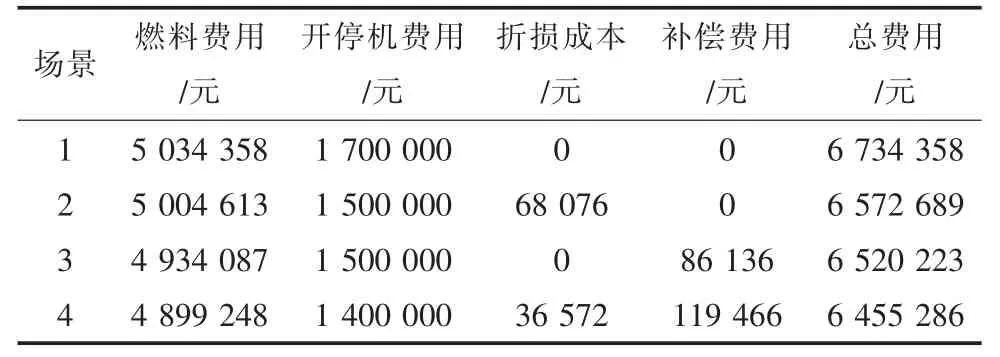
表6 不同场景下的系统运行经济性

1）场景1：基础场景运行分析。

该系统负荷与风电各时段的出力曲线如图2所示，负荷最高时段为时段11 至时段12，风电最大出力时段为时段5 至时段6，风电出力呈现出一定程度的反调峰特性，增加了部分火电机组及水电机组的调峰压力，影响系统运行的经济性。

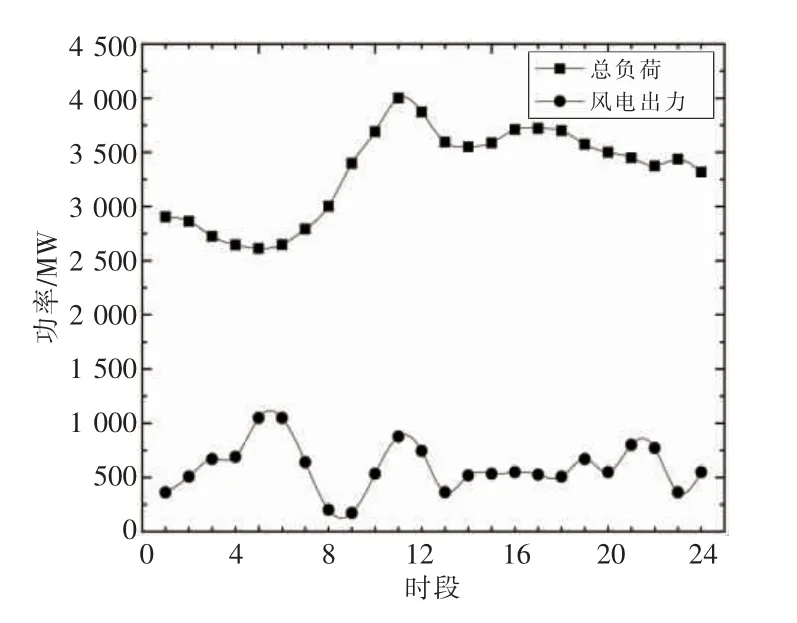
图2 各时段系统的风电出力和负荷曲线

在场景1 中，由于系统没有电化学储能和柔性负荷，只能完全依靠火电机组和水电机组发挥调峰作用。水电机组虽然调节能力较强，能够快速响应负荷的变化，但其每天的发电量受到库容的限制；火电机组受自身的爬坡速率和最小开停机时间约束；核电机组出于安全稳定运行的考虑一般不参与调峰。因此，系统的灵活调节能力不足，无法实现风电的全额消纳。在时段5 和时段6，弃风量分别达到306.57 MW 和271.06 MW，弃风率达到4.0%。同时，由于缺乏柔性负荷的响应能力，无法将部分负荷转移至风电富余时段，造成风电资源的严重浪费，增加了火电机组的燃料费用，导致系统运行效率不高，经济性较差。场景1 的火电机组开停机计划如图3 所示。

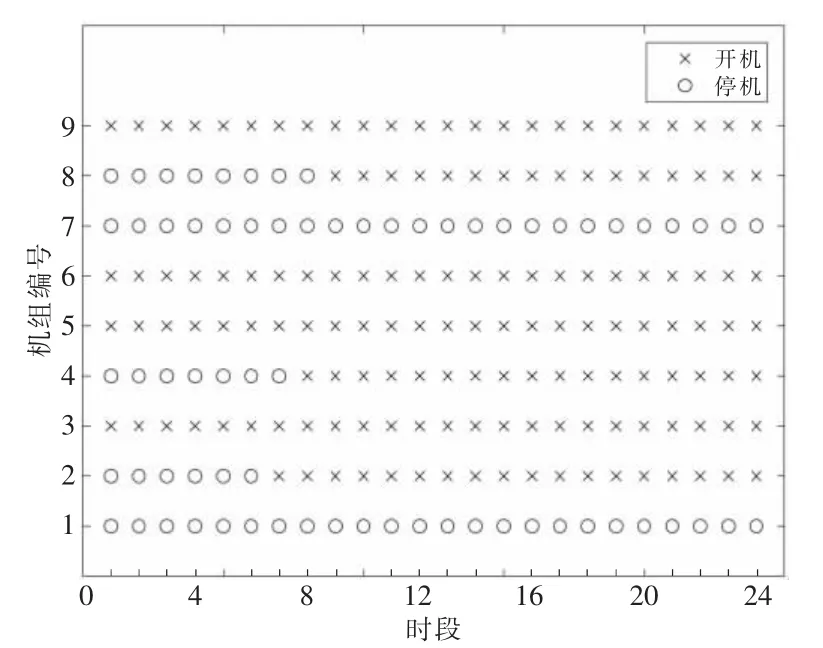
图3 场景1 的火电机组开停机计划

2）场景2：引入储能的优化结果分析。

场景2 的储能电池充放电功率如图4 所示。在场景2 中，电化学储能参与电网调度，能有效应对风电出力的反调峰特性，在风电富余而负荷低谷时将电能储存起来，用于缓解系统负荷高峰而风电出力水平较低时的运行压力，实现风电功率的转移，增强系统的调节能力，提升风电消纳率。对于场景2，时段5 和时段6 的弃风量分别为46.57 MW 和11.06 MW，相比基础场景，弃风率从4.0%下降至0.4%。由于弃风率的降低，系统的燃料费用相比场景1 从5 034 358 元下降至5 004 613 元，同比下降0.59%，系统的运行经济性显著提升。

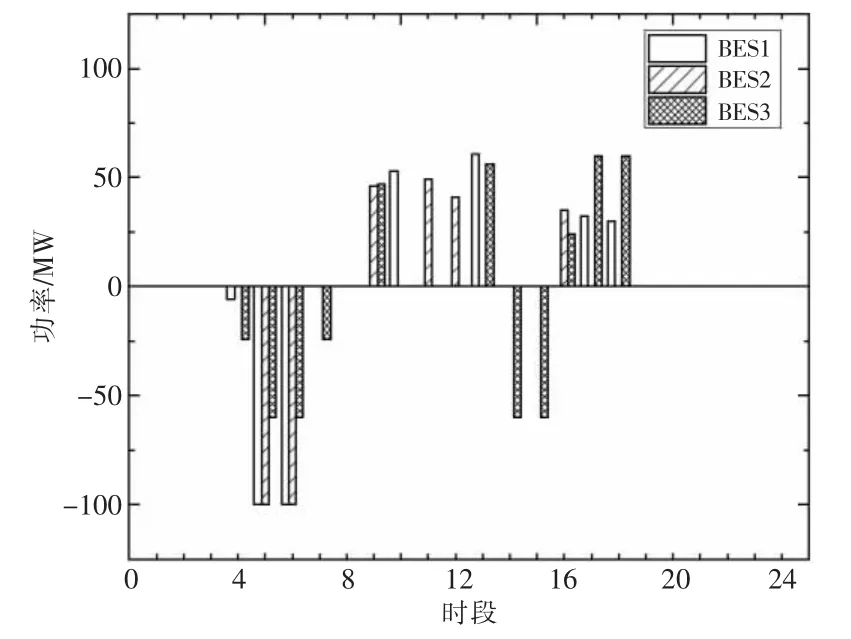
图4 场景2 的储能电池充放电功率

引入电化学储能后得到的火电机组开停机计划如图5 所示。对比图3 和图5 可知，时段1 至时段6 的负荷水平较低，此时开启的机组在整个调度周期都处于运行状态。当进入负荷水平较高的时段7 至时段24，系统配置的储能电池参与到多类型电源调度，能够提升系统运行的灵活性，因此对火电机组的调节能力需求降低，系统不需开启爬坡速率较大但费用较高的火电机组G4，而倾向于开启爬坡速率较小但费用较低的火电机组G7，这有利于减少火电机组的开停机费用，提升整体运行经济性。

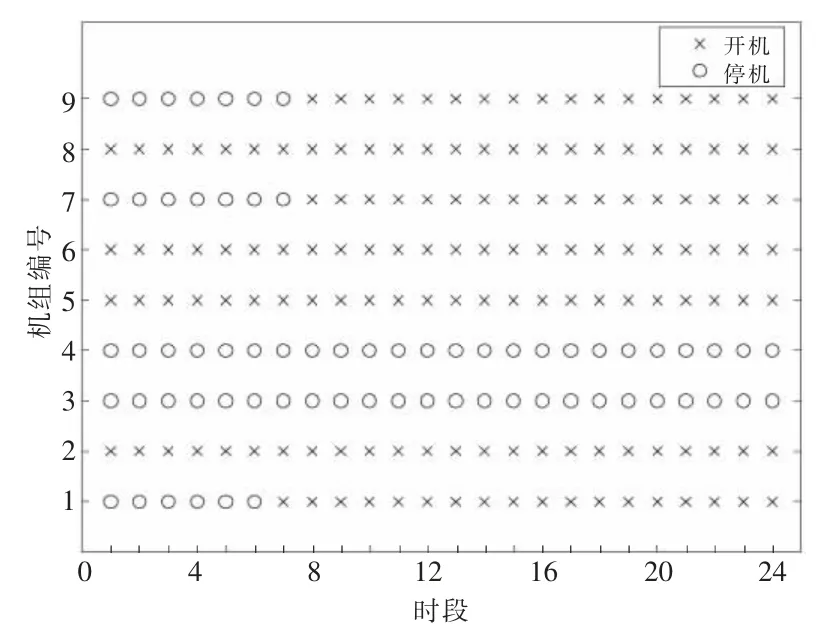
图5 场景2 的火电机组开停机计划

3）场景3：实施需求响应的优化结果分析。

实施需求响应后柔性负荷的响应情况见表7。从表7 可知，高峰时段（时段9 至时段12）的部分负荷转移至低谷时段（时段4 至时段7），必要时进行部分负荷中断。在风电富余的时段5 和时段6，火电机组和水电机组都已经下调至最小技术出力，但可转移负荷的转移量受到限制，且系统的向下调节能力不足，系统无法继续降出力来消纳更多的风电出力，因此系统无法完全消纳风电。在时段5 和时段6，弃风量分别达到42.05 MW 和5.12 MW，相比基础场景，弃风率由4.0%下降至0.33%。因此，在多类型电源电力系统中实施需求响应，能够改善负荷曲线特性，缓解系统的运行压力，场景3 的运行费用相比场景1 从6 734 358 元下降至6 520 223 元。

表7 实施需求响应后柔性负荷的响应情况

4）场景4：需求响应与储能协同优化的结果分析。

场景4 实施需求响应后的负荷曲线如图6 所示。在考虑需求响应和储能寿命约束的协同优化下，负荷峰谷差由调整前的1 387.65 MW 降低至调整后的1 121.88 MW，同比下降19.15%。场景4 中储能电池的充放电次数和放电深度相比场景2 有所降低，这表明较小的负荷峰谷差有利于制定更为经济高效的储能充放电计划。

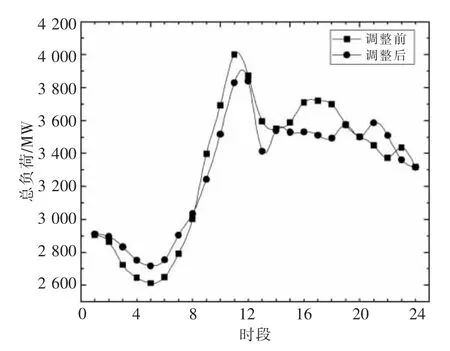
图6 场景4 实施需求响应后的负荷曲线

场景4 各类型电源的出力曲线如图7 所示。在考虑需求响应和储能电池的多类型电源协同调度方案中：核电机组作为基荷机组按照A 模式运行；按照优先消纳新能源的原则，风电机组的出力用于消纳转移至低谷时段的负荷和储能电池系统充电；火电机组出力平缓，承担大部分腰荷；水电机组和部分火电机组作为调峰机组；水电机组的调节能力较快，能够快速响应风电的随机出力和负荷变化；电化学储能和其他调峰机组协同发挥削峰填谷作用。

图7 场景4 各类型电源的出力曲线

不同场景下的火电机组负荷率见表8。可以看出，在考虑需求响应和储能电池协同调度的运行场景中，火电机组的平均负荷率相比基础场景从74.46%提升至80.67%，并且减少了一台火电机组投入运行。这表明储能参与调度运行有助于提升火电机组的运行效率，减少火电机组的开停机次数，降低火电机组的调峰压力。因此，储能和需求响应的协同优化能够降低火电机组的开停机费用，提升系统整体运行的经济性。场景4 的运行经济性为4 种运行场景中最优。

表8 不同场景下的火电机组负荷率

4.3 考虑电池寿命模型的优化对比

为了探究在考虑需求响应和储能电池的多类型电源协同调度中考虑电池寿命对调度方案带来的影响，本文设置2 种不同场景——考虑储能运行成本和不考虑储能运行成本，仿真计算得到的结果如表9 和图8 所示。

图8 储能电池的充放电功率

表9 考虑电池寿命模型的优化结果

在不考虑储能运行成本的场景中，由于在优化过程中不需考虑储能电池的折损成本，储能电池的放电深度较大，最大的放电深度达到80%。采用式（17）对不考虑储能电池折损成本的场景进行估算，其储能电池实际能够运行的寿命只有6.95年，远远小于储能电池的浮充寿命10 年。考虑储能运行成本后，整个系统的运行成本增加了1.0%。因此，在优化运行中考虑储能电池的折损成本，能够更加准确地反映调度计划的运行成本。在安排储能电池运行方式时考虑储能电池的折损成本，得到的调度方案中储能电池的放电深度有所降低，因此能够延长储能电池的使用寿命。现阶段储能的单位建设成本依然较高，折算到单位充放电功率会产生较高的折损成本，随着储能成本的降低，电化学储能将能够更大程度地提升运行经济性。