基于稀疏表示和低秩矩阵逼近的图像去噪算法的研究*

卢文锋，佀同光，韩国勇

（山东建筑大学管理工程学院，山东 济南 250101）

0 引 言

光学相干断层成像（optical coherence tomography，OCT）是一种通过测量物体后向反射光强度进行成像的技术，能够实时快速地对体内组织的表层结构进行成像.OCT系统的基本组成光路为迈克尔逊光路［1］，根据具体使用的光路器件的不同，主要分为时域OCT（time domain optical coherence tomography，TDOCT）和频域 OCT（spectral optical coherence tomography，SOCT）.TDOCT 中，宽带光源发出的光通过分束器得到2束相干光，一束照射需要成像的样品，另一束照射参考镜片；样品反射的样品光与参考镜片反射的反射光在分束器发生干涉；光路中的光电探测器将光信号转换为电信号，并发送到计算机进行处理.通过样品端机械臂的横向移动，获得不同位置的信息，参考端机械臂的移动获得某一位置的深度信息.与TDOCT系统结构类似，SOCT是在TDOCT光路的基础上用光谱仪替换光电探测器.光谱仪能够获得低相干干涉的光谱信号，通过傅里叶变换，能够一次获取某一位置纵向的空间结构信息，故SOCT系统只需样品端机械臂的横向扫描即可.

OCT系统中的样品光，可看作干涉区内被测样品所有背向散射的小波之和，样品中散射点深度分布的随机性及样品中折射率的起伏使这些小波的相位具有随机性［2］，因此，OCT图像不可避免地带有散斑噪声.而散斑噪声与成像光束的波长和成像物体的细节结构有关［3］，会降低信噪比、系统分辨率和探测灵敏度［4］.

图像的自相似性是指图像内部含有大量的非局部相似块，相似块矢量化后的矩阵是低秩的.近年来基于图像的自相似性去噪算法发展迅速.非局部均值（non-local means，NLM）算法首次应用图像自相似先验进行图像去噪［5-6］.在NLM算法中，通常通过某个邻域中所有像素的加权平均值进行滤波.然而，与每个给定像素相关联的权重并不取决于其与目标像素的几何距离，而是取决于其与目标像素的相似性.本文基于图像的非局部自相似性，首先寻找图像中的相似块［7］，然后根据稀疏表示方式和低秩矩阵近似进行去噪.

1 基于稀疏表示和矩阵逼近的去噪算法

本文提出了基于稀疏表示和矩阵逼近的去噪算法，通过对图像子块进行线性表示，代替对整幅图像进行线性表示来减少计算量，同时利用奇异值分解（singular value decomposition，SVD）在数据表示方面的巨大优势［8］.（1）通过对图像块的数据矩阵进行奇异值分解，进行全局子空间分析，确定信号子空间和噪声子空间；（2）计算图像块与信号子空间的距离，将相似的块分组为训练样本；（3）对相似块矩阵进行奇异值分解，并确定表示相似块的奇异向量；（4）去除属于噪声子空间的候选样本，即去除表示噪声的基，得到每个块的局部基.

1.1 全局子空间分析

设一幅含有噪声的灰度图像中共含有L个图像块，每个图像块的尺寸为其中n为图像中含有的像素个数.定义数据矩阵即Y中的每一个列向量为一个图像块的数据.奇异值分解表示为

鉴于SVD在表示矩阵时具有的优良特性，通过奇异值分解来解决低秩矩阵近似问题时，首先计算矩阵Y的秩r=rank(Y)，仅通过采用前r个奇异值所对应的奇异向量，重建矩阵Y［9］.即对于问题

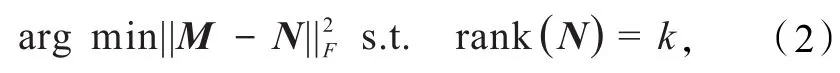
矩阵N经过式（1）的计算后，该问题的解为

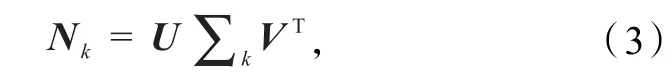
为了确定由表示信号的基构成的信号子空间，需要解决式（4）的最优化问题，

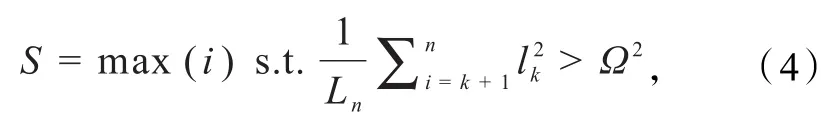
式中：S为基的数量，Ω为噪声标准差，lk为矩阵的第k个奇异值.即使噪声块与去噪块之间的平均平方残差接近噪声方差，来确定信号子空间中包含的S，从而确定前S个奇异值所对应的奇异向量来构成信号子空间.

在确定由表示噪声的基构成的噪声子空间时，运用补集的思想先来确定表示非噪声信号的基，即

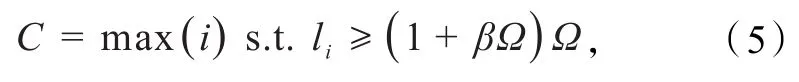
式中：参数β用来控制估计的误差，其值越大，表明噪声子空间包含向量的个数越多.确定式（5）的解即可得到表示非噪声信号基的数量C，从而确定奇异值所 对 应 的 奇 异 向 量来构成噪声子空间 .

式（4和5）中使用的噪声标准差Ω参考文献［10］中的鲁棒中值估计器（robust median estimator，RME）进行确定，即

式中：Yij∈子带HH1，HH1为小波变换中的细节子图，代表了输入图像Y水平和垂直方向的高频成分.

1.2 相似块分组与表示

利用图像的自相似性，将图像中包含的相似块进行聚类，找到每个块的训练样本.聚类的方法和实现算法多种多样，选取最简单的块匹配（block matching，BM）方法［11］.相比于在全局中寻找相似块的方式［12］，本文只在信号子空间中寻找相似块.图像块xi与xj的距离定义为

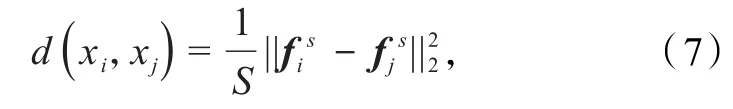
式中：S为信号子空间中包含的向量个数，已由式（4）确定为图像块xi在信号子空间中的投影向量，定义为

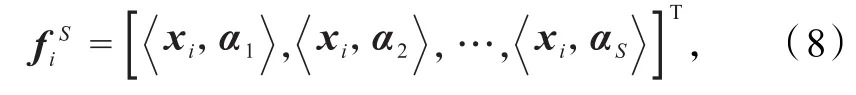
图像块的距离越小，表示二者相似程度越高，然后选取阈值Th来控制样本数据矩阵中含有相似块的数量.

相对于采取奇异值收缩重建矩阵的方法，本文将样本矩阵看作是无噪声数据，由零均值加性高斯白噪声污染后形成的，每一个样本是独立重复实验的观测结果.通过假设检验序列检测源个数的算法估计噪声标准差（σ）［13］，并基于随机矩阵理论通过一系列假设检验估计秩（r），并取前r个奇异向量得到局部基的候选向量.

1.3 去除表示噪声的基

在进行秩估计时，采取的是基于样本独立同分布的假设，在实验中并不成立，使得通过块分组得到的样本可能会有很大的差异，因此，应排除噪声占主导地位的样本和噪声子空间中的候选样本.提出2种方式来去除表示噪声的候选样本.

考虑到图像中不包含边缘结构的图像块信噪比往往较低，同时很难找到合适的样本来训练局部基，因此，第1种方式考虑重建这些图像块.在完成第1步的全局子空间分析后，对于任一图像块xi，所在组为计算图像块组的能量为

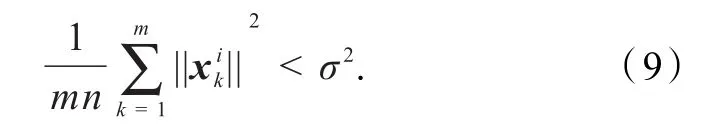
若式（9）成立，即表明该图像块所在组的平均能量较低，直接跳过第2步，用xi的平均值作为对xi的估计值；同时通过式（10）设定方差的值为

式中：参数c＞1且为常数.由于图像中含有较多的相似块，如果一个图像块是平滑的，其邻近的相似块也可能是平滑的.所以当式（9）成立时，通过参数c设置一个较大的σ值，从而检验下一个图像块来防止过拟合现象的发生.如果式（9）不成立，则继续执行第2步即可；此时σ的值仍在第2步中进行确定.

由于2个信号的相似程度可以用向量内积来表示［14］，第2种方式便是通过计算向量的内积来去除表示噪声的基.对于任一候选向量bi，计算其与每一个奇异向量的内积，找到使二者内积最大的奇异向量αi；如果αi属于噪声子空间，则去除该候选向量.

2 实验结果分析

选取真实的OCT图像进行实验，设置β=0.000 5，c=1.02，图像块的尺寸11×11，搜索窗的尺寸39×39.选取三维块匹配（block matching 3D，BM3D）算法［15］、NLM 算法［5］、奇异值分解-低秩矩阵逼近（singular value decomposition-low rank approximations，SVD-LRA）算法［16］等作为比较对象，算法中的参数均为默认值.

通常选取常见的峰值信噪比（peak signal to noise ratio，PSNR）与结构相似度（structural similarity index measure，SSIM）作为评估去噪效果的客观评价准则.PSNR通过计算对应像素点间的误差来评价图像品质，去噪效果好的算法往往对应较大的PSNR值，记为RPSN，其计算公式为

式中：Ems为均方误差，Gmax为图像灰度的最大值.SSIM从结构、亮度和对比度3个方面来衡量2幅图像相似程度.SSIM如下定义，记为ISSM

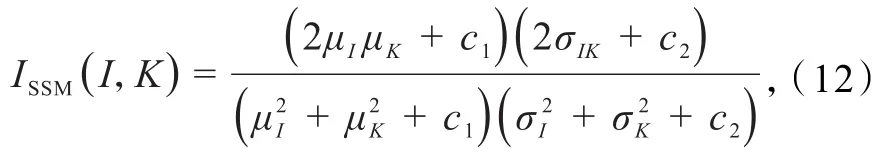
采用不同方法进行降噪处理，并计算降噪图像效果，对应图像和结果如图1和表1所示.可知，本文方法对图像OCT_1处理后PSNR为71.151 2 dB，对图像OCT_2和图像OCT_3处理后PSNR分别为74.464 9和80.587 7 dB，说明本文方法对图像OCT_2和图像OCT_3处理后降噪效果比较好，高于其他3种方法，与目前流行的BM3D方法相比具有很好的竞争力.尤其是对图像OCT_3处理后的SSIM为0.931 4，最接近于1，说明本文方法去噪后能够与原始图像保持良好的结构相似性.对于图像OCT_1，因为散斑噪声严重地影响了OCT成像品质，BM3D算法表现较好，较大程度上减少了散斑噪声，本文提出的算法和SVD-LRA算法均模糊了OCT图像，NLM算法仍保留了较多的散斑噪声；对于图像OCT_3，SVD-LRA算法也由于对图像过度平滑，使图像变得模糊而丢失细节部分，本文提出的算法有效地去除了散斑噪声而且能够保留图像中的细节信息，从视觉上优于其他3种方法.

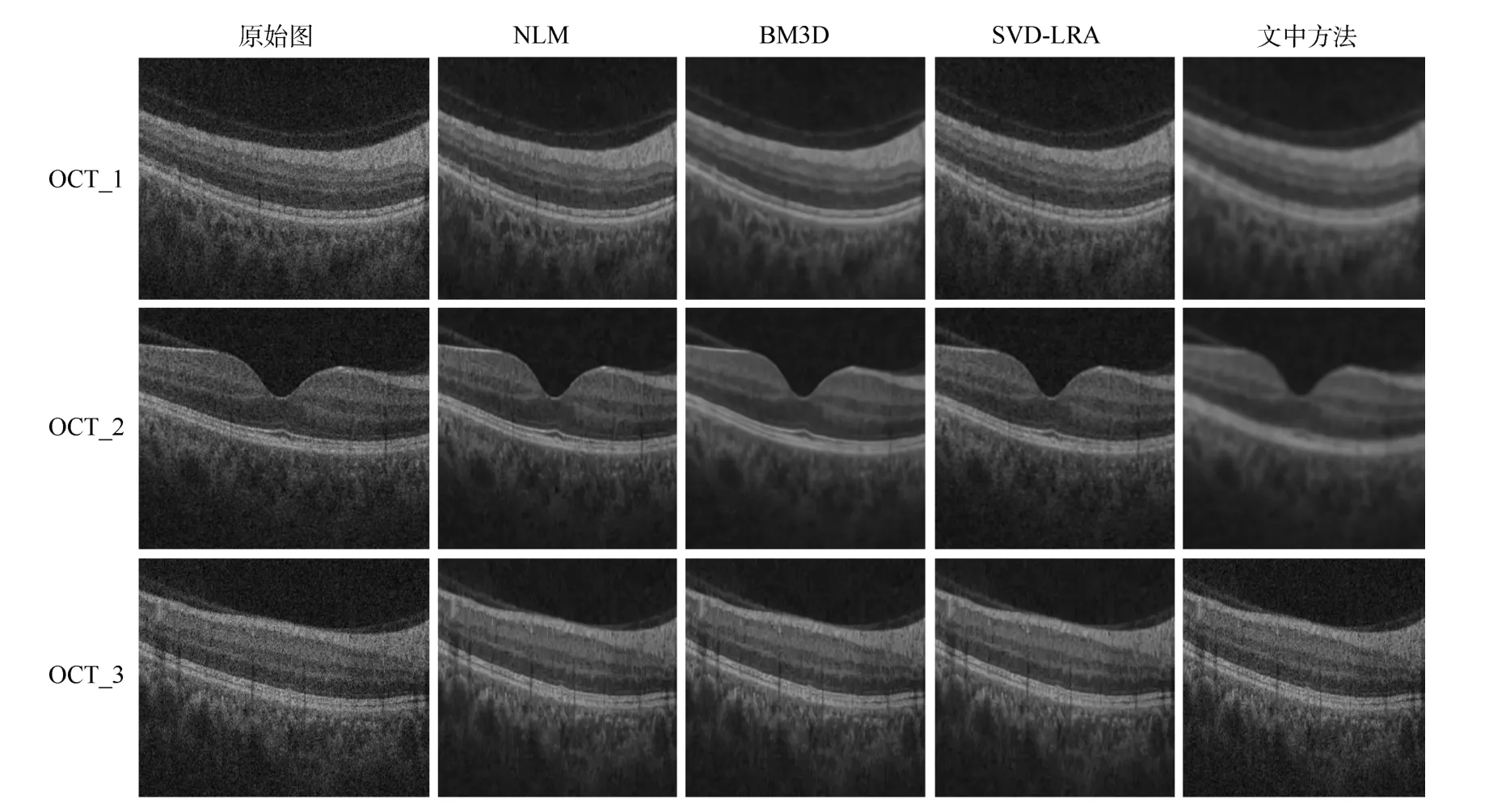
图1 3幅OCT图像经不同方法处理图像对比

3 结束语

相对于目前比较先进的降噪算法，本文提出的基于稀疏表示和矩阵逼近的图像去噪算法，具有以下优势：通过对图像子块进行线性表示代替对整幅图像进行线性表示来减少计算量；利用图像块与信号子空间的距离来寻找相似块，避免在全局中匹配相似块；充分利用了奇异值分解在数据表示方面的巨大优势，用来表示或恢复矩阵.从对OCT图像降噪实验的结果来看，相似块的选取是关键.当图像中结构相似子块较多时，本文提出的方法处理较好.如何准确而有效地选取图像相似子块，提高结构相似性匹配率是下一步要研究的问题.