考虑无功裕度的受端电网暂态电压稳定性控制方法研究
2022-01-23张运厚柳顺楠刘继成任普春关皓闻
张运厚,柳顺楠,刘继成,任普春,关皓闻
(1.国家电网公司东北分部,辽宁沈阳 110002;2.北京科东电力控制系统有限责任公司,北京 100192;3.华北电力大学,北京 102206)
0 引言
近年来,随着我国电力系统规模的不断扩大和可再生能源、多源储能、多能源转换等接入容量的快速增加,远距离大容量输电系统的功率平衡问题日趋复杂[1]。多能源接入与大规模跨区域外送,使电网在经历大扰动时,电压稳定控制变得更加困难[2]。
国内外学者针对电网暂态控制过程进行了大量研究。文献[3],[4]进行了系统安稳控制策略研究,探讨了基于暂态过程能量平衡控制的离线决策控制方法和在线预决策控制方法;两者的策略表生成方式分别通过离线手动计算和计算机在线计算。文献[5],[6]采用稳定性能指标作为暂态能量控制约束条件;通过反向积分计算得到当前故障的线性不等式;通过迭代计算得到最优机组功率控制策略。文献[7]将故障切除时刻的发电机的转子角速度和动能作为暂态能量平衡控制策略优化的关键数据,进行电网下一时段的稳定控制。文献[8]综合系统拓扑和暂态功率控制前后发电机同步系数进行动态网络同步,通过电力系统线性和非线性模型确定最优功率控制策略,得到系统的切机量。文献[9]基于转子运动方程,分析电力系统在正常工况下、故障切除时刻和采取机组功率控制时刻的运行特性,提出一种求取最小功率控制切机量的方法。
电压稳定裕度(VSM)的大小与无功容量正相关。文献[10]提出了一种考虑可信度的可再生能源出力方法。该方法将能量裕度要求作为一个非线性优化问题,进行系统能量平衡优化控制,采用Bender分解法进行模型求解。文献[11]以最大限度地增加无功备用容量及降低系统无功损耗为目标,采用了一种双目标优化控制方法。该方法采用基于最优潮流和Bender分解的非线性优化框架来确定系统最优运行条件。文献[12]引入了基于无功储备约束的最优潮流概念,利用最优潮流框架确定在各种工况和运行条件下,提高电压稳定裕度所需的最小无功电源数量。文献[13]以最大限度地提高电压稳定裕度为目标,实现了系统成本和电压稳定裕度的多目标优化。以上研究主要针对电力系统暂态过程控制,通过控制机组的出力以及相应的无功电源,实现系统有功、无功稳定。但是,目前对于跨区域受端电网的暂态稳定控制研究较少,并未涉及相关电压稳定裕度控制的研究。为解决受端电网暂态电压稳定性问题,对受端系统电压稳定实现精确控制,本文通过分析受端系统暂态电压稳定性条件,结合系统无功裕度计算方法,通过建模得到受端系统的电压稳定性曲线;通过电压稳定预测方法进行优化学习,判断受端系统电压的稳定性。
1 无功裕度与电压稳定性分析
受端电网的无功裕度计算式[14]:

式中:X=[x1,x2,…,xm-1,xm]T,x1,x2,…,xm-1,xm为描述电力系统当前状态的m个状态变量,为电力系统所有节点各自的电压幅值、相角、有功功率、无功功率。
2 系统最大无功裕度优化
在跨区域电力系统中,受端系统电压稳定性受系统无功补偿及无功电源容量的影响。由于无功功率很难通过外送系统获得,因此为保证受端系统的电压稳定性,必须保证受端系统装有足够的无功电源及无功补偿装置。受端系统无功裕度是指系统电压能够在保持稳定范围内所需的无功支撑。为了使系统电压有较大的弹性波动范围,可通过增大系统无功支撑容量使系统无功裕度最大,从而进行电网电压稳定性的控制。系统无功最大裕度表示为
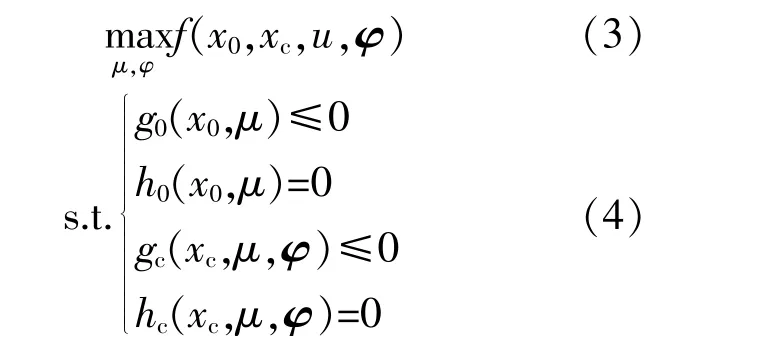
式中:目标函数f(·)为受端系统无功裕度计算函数;μ为控制变量,是由发电机的输出电压和输出无功功率组成的向量;x为控制变量在当前工作点和崩溃点的电压值;φ为状态变量向量,即虚拟无功功率注入向量;g(·),h(·)分别为系统不等式约束和等式约束,等式约束条件由系统当前工作点的潮流方程及控制变量构成,不等式约束由机组运行极限、输电线路节点电压幅值构成。
无功裕度计算目标是发电机正常运行时与最大无功输出运行时的差值最小,目标函数由式(5)给出。在工作点和电压崩溃点受给定等式和不等式约束,如式(6)~(13)所示。
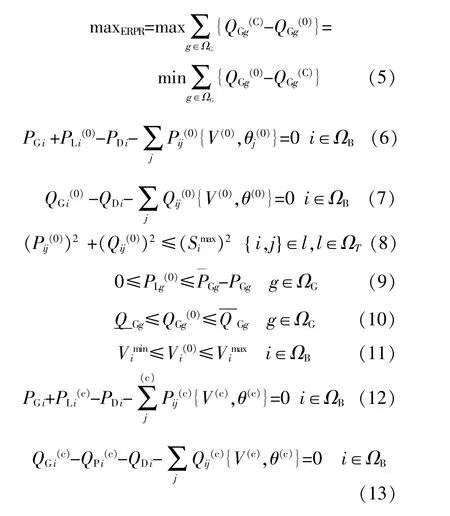
式中:ΩB,ΩT,ΩG分别为母线的集合、线路的集合和发电机的集合;i,j为母线相关参数;l为线路参数;g为发电机参数;Vi为母线i的电压幅值;θ为连接两个节点母线之间的电压角差;P,Q分别为有功功率和无功功率;PGi,PLi,PDi分别为i母线的有功发电量、损耗量和需求量;Pij为各总线ij之间的有功功率流;QGi,QDi为母线内的无功发电量和需求量;Qij为ij母线间的无功流量;QPi为注入第i母线的无功功率矢量。
3 受端电网电压暂态稳定模型
跨区域受端系统电压稳定性是指送端电力系统中出现功率波动或受端出现扰动后,保持系统中所有母线电压稳定的能力。本文主要针对在受端系统负荷突然变化的情况下,因系统无功支撑容量不足所进行的电压稳定性控制。
当负载需求功率超过最大可输出功率时,系统会出现电压波动。正常情况下,系统电压位于电压崩溃临界点上方,其中受端系统负荷需求与负载母线电压大小之间的关系如图1所示。


在进行无功备用(RPR)计算后,利用优化控制方法来增加系统的无功稳定性裕度。首先将无功备用容量和电压稳定裕度(VSM)提高到安全水平所需的最大值内,电压稳定裕度取值为0.92~1.05 p.u.。


不等式(16)约束保证将关键无功备用恢复到最小容量限制;不等式(17)确保电压稳定裕度恢复到更高水平。

不等式(18)表示电压极限采用线性灵敏度。公式(19)的约束保证在恒定功率因数情况下减载,给定负载u的相位角为θLu。为减少负荷,考虑母线的最大值,式(20)~(23)对控制变量进行限制,以确保控制量在允许的控制范围内。
4 基于受端系统无功裕度动态分配
受端系统要充分利用无功补偿装置和无功电源的无功调节容量及调节能力。当系统无功容量不能满足系统电压调节需要时,利用无功补偿装置对受端系统进行无功调节。在进行受端系统无功协调控制时,首先应充分利用受端系统本身发电单元的无功调节裕量,预留尽可能多的无功补偿装置调节裕量,以应对送端电网的暂态波动。
受端系统无功分配方法如下:假设在节点i处的无功补偿容量为QNi,在节点i处的无功补偿装置的输出无功功率的初始分配因子如式(24)所示。

式中:Qbc为无功补偿装置的总容量;m为各节点处投入无功补偿装置的数量。
通过以上分布因子的计算,求解无功调节容量ΔQ在节点i处的无功补偿装置的补偿量为ΔQi。

对各节点处无功补偿容量的调节裕量进行校验,若满足调节条件,方案通过;若无功补偿装置的无功调节裕量不足时,则须进行相应方案的调整。设无功调节容量不足节点的无功补偿单元的集合为ΩLack,ΩLack中包含M个元素。调节裕量不足无功补偿装置的当前调节容量为

通过以上方法,形成调节裕量匮乏的无功补偿装置和裕量充裕的无功补偿单元无功功率调整量分配系数。
5 跨区域受端电网电压稳定性控制方法
通常情况下,跨区域受端电网可通过多个通道受电,其电压稳定水平与单通道无功分配裕度相关,多个通道之间无功裕度均衡性越好,受端电网受电能力越高。采用多通道裕度均值和多通道裕度标准差之和的关联性,表征多通道受电系统暂态受电能力指标。为提高受端系统电压稳定性水平,采用无功裕度控制方式[15],[16]。
计算单通道无功裕度指标,该系数反映单通道无功裕度期望值:

受电比例能够反映受端电网的受电能力,受电比例越高,表明受端电网网架结构越强,受电能力越强。受电比例确定步骤如下:①确定系统的多个通道,建立多通道受电系统的内、外通道模型;②根据模型计算外部通道的无功裕度指标和暂态无功分配系数,同时根据模型计算内部通道暂态无功系数;③根据外通道无功裕度指标和暂态无功分配系数计算多通道受电系统暂态稳定裕度;④基于多通道受电系统暂态稳定裕度、内通道暂态无功分配系数和负荷功率因数,计算多通道受电系统最大受电比例。
为提高跨区域多通道受端电网受电比例计算的速度及准确度,首先应建立电压稳定控制训练数据库,数据库由N个运行点数据组成,其中包含D个数据通道。该数据库由相量测量单元(PMU)记录,每一个运行节点数据均由测量电压和电流的幅值和相位角数值表示。同步相位矢量Xi=[Xi1,Xi2,…,XiN]T表示i个运行点。其中,Xij是特征量,或当系统在工作点i从通道j记录的一定电量的值。集合DU是未标记的数据集合,DU=[X1,X2,…,XN]。对于每个运行点,与Xi对应的矢量为Yi,其向量形式表示为y=[Y1,Y2,…,Yi]。
通过以上矢量数据计算,采用标记的数据集进行机器学习训练,其控制学习模型为f。通过机器学习,可以预测下一时刻系统的不确定元素xj,为控制过程提供电压稳定性控制近似值。通过学习建立对应的数据库,标记每个元素的最佳学习状态。给定未标记的数据DU,可通过学习找到与之对应的目标DL,从而提高在当前目标上训练的机器学习模型的预测精度。
基于主动学习的受端系统电压稳定预测方法如图2所示。利用机器学习模型的不确定性来选择数据点进行标注。在每次迭代中,经过部分训练的分类器从未标记的数据库中选择部分不确定的因子。

图2 电压稳定性学习控制流程Fig.2 Voltage stability learning control process
6 算例分析
在改进的IEEE33节点系统上进行仿真,其中无功补偿装置的接入节点如图3所示。
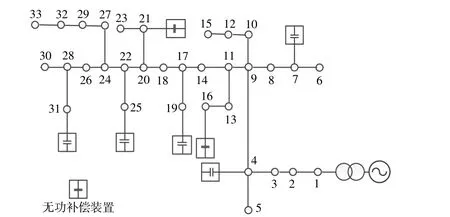
图3 仿真系统Fig.3 Simulation system
采用基于无功裕度的电网电压稳定控制方法对某区域受端系统进行仿真分析。该受端电网中在7个节点处安装无功补偿装置,各节点处电压无功补偿装置的容量以及各节点的电压如表1所示。各节点电压的上限和下限分别为1.05 p.u.和0.95 p.u.。

表1 节点电压及无功补偿容量Table 1 Node voltage and reactive power compensation capacity
图4为采用基于无功裕度的电压稳定控制方案下某节点发生故障后母线电压恢复曲线。由图4可见,采用优化控制后得出的控制方案在电网发生故障后母线电压恢复更快,系统暂态电压稳定性更好。
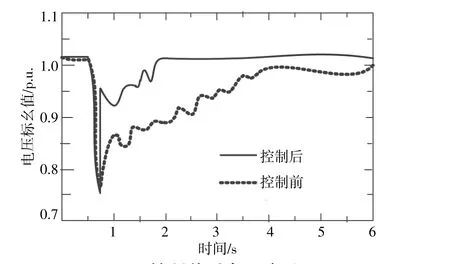
图4 控制前后电压波形Fig.4 Voltage waveform before and after control
从表1可以看出,采用基于无功裕度预测的电压稳定控制方案后,节点4、节点7、节点21和节点31处的接地电压和无功需求裕度均较高。这是因为在该节点处接入负荷中心220 kV网架,对负荷中心的暂态电压支撑作用最为明显。故障前无功补偿装置的出力为1 p.u.,故障切除后的暂态过程中无功补偿发出的最大无功功率为1.06 p.u.,可见提高无功补偿装置的无功裕度,可有效增加故障切除后机组的动态无功功率输出,对系统暂态电压的支撑起到了很好的作用。节点处无功补偿装置出力情况如图5所示。

图5 无功补偿装置补偿容量Fig.5 Compensation capacity of reactive power compensation device
采用所建立的模型获得的暂态电压稳定裕度值非常小,仅为0.006 8,表明其具有非常高的评估精度。图6所示为暂态电压稳定裕度评估结果。图6中曲线清楚地展示了电压稳定预测模型的评估裕度与实际值的贴近程度,且具有同步的变化趋势。电压稳定的整体效果良好,最大偏差不超过0.01,完全能够满足实际评估应用的需要。
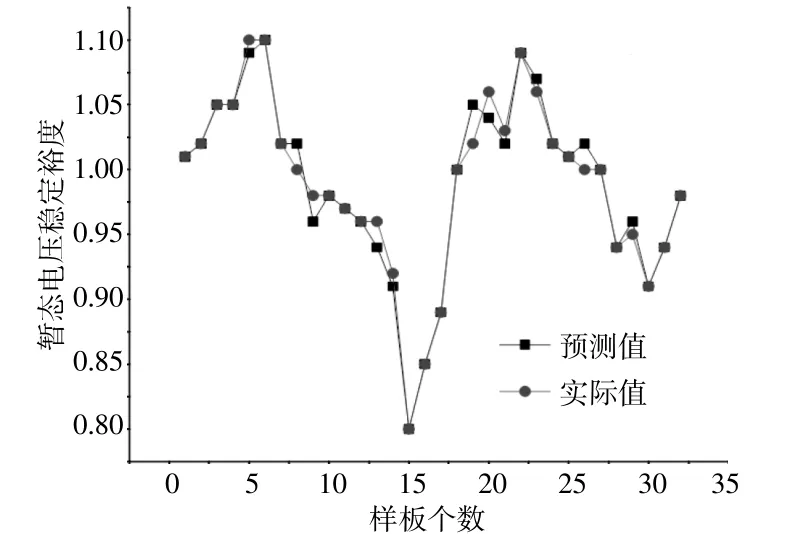
图6 暂态电压稳定预测结果Fig.6 Transient voltage stability prediction results
7 结束语
针对受端系统的仿真算例及其仿真结果的分析表明,本文提出的受端系统暂态能量电压稳定控制模型,在无功控制精度和实时控制的时效性方面均具有较好的控制效果。
本文根据无功与电压稳定性关系提出了基于无功裕度的主动学习方法,通过为机器学习模型建立数据集,进行高效的数据学习预测,可获得精确的预测结果。
