基于频谱包络改进的EWT方法的滚动轴承故障诊断研究

唐诗尧，何佳，任锦胜，吴仕明，柳亦兵

（1.华润电力技术研究院有限公司，广东深圳 518000；2.北京英华达电力电子工程科技有限公司，北京 100022；3.华北电力大学电站设备状态监测与控制教育部重点实验室，北京 102206）

0 引言

近年来，为应对日益严重的能源与环境危机，风力发电技术发展迅猛。滚动轴承是风电机组传动链的重要部件，目前普遍采用测量和分析轴承振动信号的方式对其进行故障诊断。轴承故障产生的摩擦和冲击，通常体现为频谱中的谐波成分。轴承故障振动信号存在冲击现象，一般通过频谱分析和包络谱分析可识别故障特征频率[1]。然而，如果轴承同时存在多点复合故障，且信号中噪声干扰较大，容易造成对轻微故障成分的漏诊。信号分解方法可以增强故障特征信息，提升故障识别效果[2]，是一种有效的轴承故障特征提取方法。

风电机组振动监测模式主要依靠独立数据监测和人工分析诊断[3]。Huang N E[4]提出了经验模态分解算法（EMD），并加入小波理论框架[5]。EMD方法是一种有效的特征提取方法，然而该方法存在端点效应和迭代计算导致的效率低下问题[6]。Frei M G[7]提出了固有时间尺度信号分解算法（ITD），但该方法使用线性方法进行信号分解的基线拟合，所得模态会出现失真现象[8]，[9]。Gilles J提出了经验小波变换（EWT）[10]算法，这种算法既有经验模式分解的自适应性，也有小波变换的多尺度特点。该方法具备无端点效应、无失真且运算快捷等优势[11]，受到研究者的重视。但是EWT算法存在需要人为设置频谱分割数量的问题，影响了其在工程中的应用。

为了完全不需要设置频谱分割数量，研究人员进行了大量研究。文献[12]引入了尺度空间原理，改进了EWT算法，利用ε邻域方法划分信号的频谱，从而无需预设边界数量。文献[13]提出了一种基于无参数经验小波变换（PEWT）和余量因子的自适应故障检测方法，并对故障滚动轴承信号进行分解，证明了该方法的有效性。文献[14]通过截取短时间信号进行傅里叶变换，将短时间信号的低分辨率频谱当作原始信号频谱的简单包络，在频谱的包络中寻找极小值点并作为边界。这些研究成果在一定程度上改善了自适应频谱分割的使用效果，但这些方法受频谱中底噪的影响，底噪鲁棒性较差，容易产生多余分量且分割方法缺乏实际意义，不符合振动信号故障分布机理，难以将故障成分合理筛出。

针对现有EWT算法的缺陷，本文提出了一种改进的EWT频谱分割方法。通过分割因子对频谱进行分段取极值，达到对故障信号幅值谱进行简单包络的效果，然后通过界限因子筛选的幅值谱包络的局部最小值作为分割边界，最后利用Meyer小波分解提取出模态分量。该方法具有原理简单，运算方便且符合振动信号故障分布机理的优点，解决了EWT算法需要人为设置分割数量和不考虑故障机理的问题。由于设置了阈值c，使该方法不受信号底噪的影响。通过两种滚动轴承故障案例进行验证，结果表明该方法对实际轴承故障诊断有效，且较传统EWT方法在故障特征提取方面具有一定优势。

1 改进EWT方法

EWT首先将信号进行傅立叶变换，得到信号的频谱。将频谱分割为N个频率区间，各分割的区间定义为

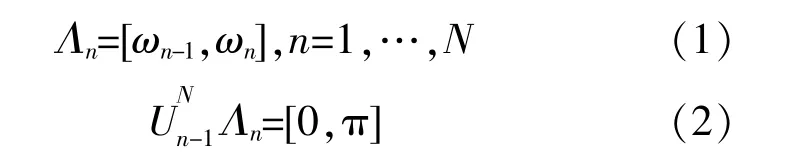
式中:ω为小波带通滤波器的截止频率；U为全集。

围绕每个ω都定义一个过渡段τn（宽度是2τn），除去起点与终点两个边界，需要N+1个分割边界。

频谱区间划分的方法是，将频谱中所有的极大值点找出，共M个。将这些极大值从大到小依次排列。若M大于N，保留局部极大值点的数量为前N-1个；若M小于N，则保留所有的局部极大值点，将N值取为N=M。最后，确定频谱分割的边界，边界ω是两个局部极大值点的中间点。图1为频谱分割图。

图1 频谱分割Fig.1 The segmentation of spectrum

在确定了每个分段区域后，对每个频率段Λn设计正交小波带通滤波器组。使用的小波是Meyer小波，其尺度函数ϕˆn和小波函数ψˆn分别为

式中:γ，β均为经验参数。

取滤波器过渡带带宽为2τn，令τn=γωn，0＜γ＜1。

重构公式得:

在自适应诊断方向上，经验小波变换有很大的发展前景。理想情况下，通过准确分割频带，再使用小波变换进行带通滤波，即可分解出不同故障的信号分量，实现故障诊断识别。

1.1 轴承故障特征分析

滚动轴承的常见故障有疲劳、磨损、腐蚀和电蚀等损伤[15]。轴承处于正常状态时，由于润滑油膜的作用，轴承的滚动体和内外滚道很少有直接接触，振动信号以随机噪声为主，调制和冲击成分较少，频谱中边带成分较少。而当轴承发生故障时，滚动体和内外滚道在故障点产生冲击，振动信号频谱中会出现幅值调制产生的边带成分。图2为多种故障轴承频谱示意图。

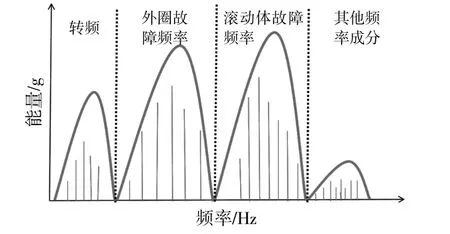
图2 多故障轴承频谱Fig.2 Frequency spectrum of complex-faulty bearing

1.2 改进分割方法

式中:n为采样点数；fs为采样频率；Fz为分段频率。

Sf的设定与最终的分段效果有关，它表示频谱中的点数，Fz要大于或等于2倍的轴承内圈故障频率，以免选中的局部极大值处于两条以故障频率为间隔的边带之间，导致分割出多余的分段。

将频谱分割为l份，每份记作Ai。前l-1份中有Sf个点，将剩下少于Sf个点的部分作第l段，寻找每份频谱中的极大值mi。

求出Ai中所有局部极小值pn。pn是EWT运算中每个模态频率的分割边界。设定阈值c，如果pn＜c，则忽略该极小值。这样做有利于消除噪声对于频谱分段的影响。

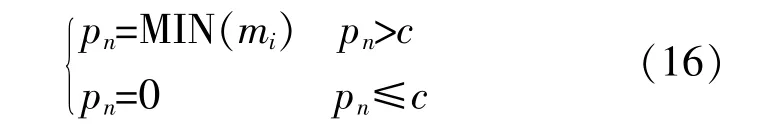
图3为该方法的频谱分割示意图。图3中每个分段的最大值构成频谱的简单包络，有效地简化了频谱的复杂结构，避免了频谱中的局部变化对于分段结果的影响。参照该种方法先得到若干个边界pi，再通过EWT中小波变换的方法来进行剩下的步骤，重构各个部位的信号成分。

图3 改进EWT频谱分割Fig.3 Segmentation of frequency spectrum by improved EWT

2 仿真分析

使用仿真信号来验证该分割方法的实用性，该信号由随机噪声和调制冲击成分组成，模拟了轴承故障的信号特征。

仿真信号为

式中:采样频率fs为12 800 Hz；载波频率fm为3 000 Hz；故障调制频率fc为90 Hz；信号长度n为12 800点。

图4为使用本文提出的频谱分割方法处理仿真轴承信号数据的结果。频谱上方的连线是频谱的简单包络线。由图4可知，改进分割方法将模拟信号分为5段。

图4 仿真信号频谱分割Fig.4 Segmentation of frequency spectrum of simulation signal

图5为仿真信号分解结果图。由图5可知:第二、三模态包含了故障特征；包络谱中存在明显的故障频率。这说明本文提出的改进EWT算法成功提取了冲击成分，本方法对模拟轴承信号有效。

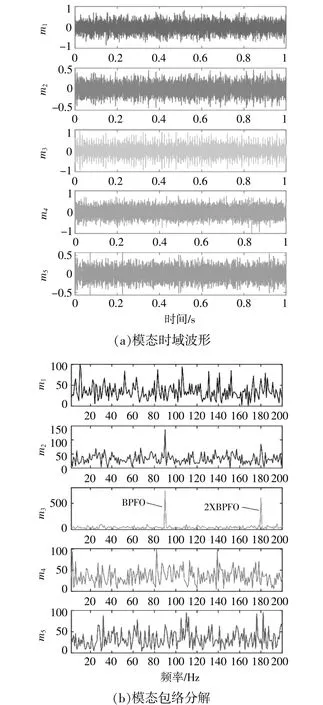
图5 仿真信号分解结果图Fig.5 Simulation signal decomposition result graph

3 现场案例与应用

利用某风电场的风力发电机滚动轴承复合故障信号对本文方法进行验证。故障机组的型号为FD-77，该机组装备有北京英华达在线振动监测系统。图6为测点示意图。

图6 测点示意图Fig.6 Schematic diagram of measuring point

该机组的发电机配备3个滚动轴承，其中驱动端深沟球轴承组合圆柱滚子轴承，自由端有一个圆柱滚子轴承。深沟球轴承型号为SKF 6330/C3VL207，圆柱滚子轴承型号为NU1030 ML SKF。轴承故障频率见表1。

表1 轴承故障频率Table 1 Ball pass frequency of bearing

某台机组驱动端轴承测点报警，经振动分析人员确认，驱动端深沟球轴承存在较为严重的故障。现场人员拆下检查，发现驱动端滚动轴承的外圈和滚动体均有严重损伤。

图7为故障期间的时域波形以及频谱曲线图，转频为29.2 Hz，转速为1 752 r/min。

图7 故障轴承波形频谱Fig.7 Wave and frequency spectrum of faulty bearing

图8为故障轴承信号的包络谱图。图8中明显存在保持架故障频率11.7 Hz及其倍频。保持架故障频率的9倍频与外圈故障频率接近，易误导诊断人员忽略外圈故障频率，误判为单纯的保持架或滚动体故障。

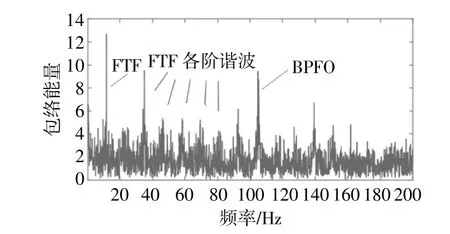
图8 故障轴承包络谱Fig.8 Frequency spectrum envelope

使用改进EWT方法对轴承故障信号进行频谱划分，结果如图9所示。

图9 改进EWT对频谱的分割Fig.9 Segmentation of frequency spectrum of complex-faulty bearing by improved EWT

图10为改进EWT分解图。由图10可知，轴承的外圈故障频率清晰地在第2和第5个模态中显现，第3和第4个模态的包络谱中清晰地显示出保持架故障频率。因此，改进的EWT方法能够将两种故障频率分离，有助于准确诊断故障。

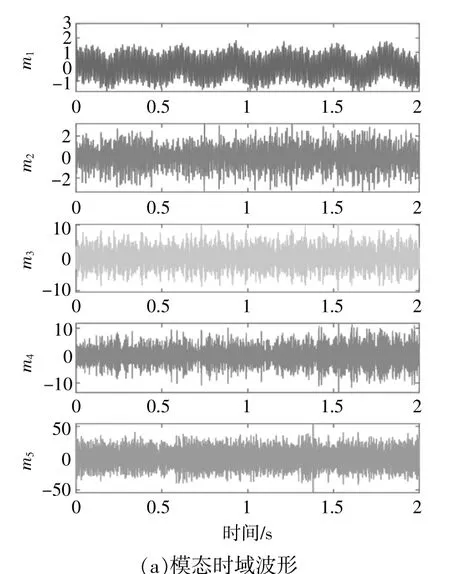
图10 改进EW T模态及包络谱Fig.10 Mode and spectrum envelope of improved EWT

使用原始方法对频谱进行分割，须要设置分段的个数。参考改进分割方法的分解结果，将分解数设置为5。

利用EWT的原始分割方法对案例信号进行处理的结果见图11，12。

图11 传统方法的频谱分割Fig.11 Segmentation of frequency spectrum of complexfaulty bearing by original EWT

由图12可知:按照传统方法同样可以将外圈故障频率提取出来，在模态2和模态3中外圈故障频率和保持架故障频率同时存在于模态；本文提出的方法的分解结果中保持架和外圈频率被完全分离。这说明相对于原始分割方法，本文提出的方法的分离精度更高。

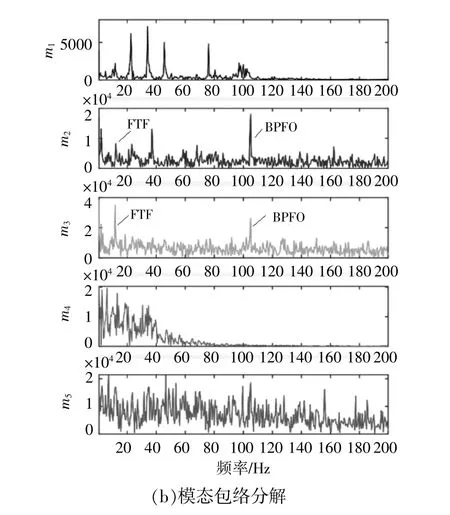
图12 原始EWT方法的模态及包络谱Fig.12 Segmentation of frequency spectrum of complexfaulty bearing by original EWT

现场检查该轴承时发现，该轴承外圈故障已经很严重，滚动体也严重剥落变形。检查结果如图13所示。由于滚动体变形，信号中存在保持架故障频率成分。

图13 故障轴承照片Fig.13 Photo of complex-faulty bearing

4 结论

EWT的分解精度依赖于有效的频谱分割，目前的频谱分解方法需要人为设置分段数量，不符合实际应用的需求。各类自适应分解方法的噪声鲁棒性较差，易引发分解数量太多，影响分析效果。本文提出的改进的频谱分割方法通过分割因子对频谱进行分段取极值，从而达到对故障信号幅值谱进行简单包络的效果，再综合界限量子找出幅值谱包络的局部最小值，作为EWT方法的分段界限。本文方法具有以下优点。

①无需设置分段数量，可自适应确定模态数量。

②不受底噪和频谱局部变化的影响，鲁棒性较高。

③多故障情形下分离效果较好，分离精度高。