标准拉普拉斯分布次序统计量的性质
2022-01-22尹真真邱珍珠
尹真真, 邱珍珠
(上海对外经贸大学 统计与信息学院,上海 201620)
1 引 言
次序统计量是数理统计中的重要概念之一,它在可靠性理论、参数估计和非参数估计等领域有着广泛的应用.比如,串联系统的正常工作寿命为X(1)=min(X1,X2,…,Xn),并联系统正常工作寿命为X(n)=max(X1,X2,…,Xn).陈光曙[1]研究了最小次序统计量和最大次序统计量的联合分布函数,并进一步给出其研究结果的实际应用.关于两参数拉普拉斯分布已有许多文献做过研究.徐晓岭、顾蓓青和王蓉华[2]研究了两参数拉普拉斯分布(L(α,β)),由于它与正态分布相比具有尖峰厚尾的特性,因而在工程科学、质量控制、环境科学以及金融工程等领域得到了广泛的应用.徐晓岭和王蓉华[3]通过构造四个独立同分布于标准正态分布的随机变量的函数得到了标准拉普拉斯分布.匡能辉[4]证明了两参数拉普拉斯分布总体的样本的次序统计量间隔(X(1),X(2)-X(1),…,X(n)-X(n-1))既不独立也不同分布.钱开燕和宁荣建[5]主要研究了指数分布与二项分布、泊松分布、正态分布、均匀分布之间的联系.拉普拉斯分布的应用十分广泛,例如其在研究股指收益率中就经常被用到[6-9].本文主要针对样本容量为2的标准拉普拉斯分布总体,研究其次序统计量X(1),X(2)分布的一些特殊性质.
2 标准拉普拉斯分布极大、极小次序统计量的分布
设随机变量X服从标准拉普拉斯分布,记为X~L(1),其分布函数F(x)与密度函数f(x)分别为
针对标准拉普拉斯分布L(1),易得到如下引理1:
引理1设随机变量X服从标准拉普拉斯分布,则
(i)F(-x)=1-F(x);

(iii)-X~L(1);
(iii)|X|~Exp(1).
设总体X~L(1),样本容量n≥2,X1,X2,…,Xn为总体X的一个简单随机样本,其次序统计量记为X(1),X(2),…,X(n),极小、极大次序统计量的分布由如下定理1给出.
定理1(i)极小值次序统计量X(1)的分布函数FX(1)(x)与密度函数fX(1)(x)分别为
(ii)极大值次序统计量X(n)的分布函数FX(n)(x)与密度函数fX(n)(x)分别为
(iii)X(1)与-X(n)同分布,X(n)与-X(1)同分布.
证(i)对-∞ FX(1)(x)=P(X(1)≤x)=1-P(X(1)>x)=1-P(X1>x,X2>x,…,Xn>x) (ii)对-∞ FX(n)(x)=P(X(n)≤x)=P(X1≤x,X2≤x,…,Xn≤x) (iii)由于标准拉普拉斯分布是对称分布,由引理1可知:X与-X同分布而X(1),X(2),…,X(n)为来自L(1)总体的前n个次序统计量,-X(n),-X(n-1),…,-X(1)为来自L(1)总体的前n个次序统计量,即有X(1)与-X(n)同分布,也即X(n)与-X(1)同分布. 特别地,当n=2时 定理2设总体X~L(1),X1,X2是来自总体X的两个简单随机变量,X(1),X(2)为其次序统计量,则有如下结论: (ii)|X(1)|和|X(2)|的分布函数与密度函数分别为 F|X(1)|(x)=F|X(2)|(x)=2F(x)-1,f|X(1)|(x)=f|X(2)|(x)=2f(x),x>0; (iii)X(1)与X(2)的联合分布函数为 证(i)对x≥0 进而 (ii)对x≥0 F|X(1)|(x)=P(|X(1)|≤x)=P(-x≤X(1)≤x)=FX(1)(x)-FX(1)(-x) =2F(x)-[F(x)]2-2F(-x)+[F(-x)]2=2F(x)-1, F|X(2)|(x)=P(|X(2)|≤x)=P(-x≤X(2)≤x)=FX(2)(x)-FX(2)(-x)=2FX(x)-1, 进而 f|X(1)|(x)=f|X(2)|(x)=2f(x). (iii)对-∞ FX(1),X(2)(x1,x2)=P(X(1)≤x1,X(2)≤x2)=P(X(2)≤x2)-P(X(1)>x1,X(2)≤x2), 若x2≤x1 FX(1),X(2)(x1,x2)=[F(x2)]2, 若x2>x1 P(X(1)>x1,X(2)≤x2)=[F(x2)-F(x1)]2, FX(1),X(2)(x1,x2)=F(x1)[2F(x2)-F(x1)], 则X(1)与X(2)的联合分布函数为 (iv)对-∞ 类似地,对x1≥0,-∞ (v)对x1,x2≥0 若x1≥x2 若x1 由定理2可以得到如下结论: (i)X(1),X(2)既不独立也不同分布; (ii)X(1)与-X(2)同分布,X(2)与-X(1)同分布; 并由此得到“不独立的随机变量X,Y,其函数可能独立,也可能不独立”这一结论. 定理3设总体X~L(1),X1,X2是来自总体X的两个简单随机变量,X(1),X(2)为其次序统计量,则 (i)|X1|与|X(1)|同分布,|X2|与|X(2)|同分布; (ii)|X(1)|与|X(2)|独立同服从Exp(1); (iii)|X1|-|X2|,|X(1)|-|X(2)|同服从L(1). 证(i)显然成立; (ii)对x≥0,F|X(1)|(x)=F|X(2)|(x)=2F(x)-1=1-e-x,即|X(1)|与|X(2)|同服从标准指数分布Exp(1). 又对x1≥0,x2≥0 F|X(1)|,|X(2)|(x1,x2)=P(|X(1)|≤x1,|X(2)|≤x2)=P(-x1≤X(1)≤x1,-x2≤X(2)≤x2), 若x1≥x2 F|X(1)|,|X(2)|(x1,x2)=[F(x2)]2-F(-x1)[2F(x2)-F(-x1)]-[F(-x2)]2 +F(-x1)[2F(-x2)-F(-x1)]2=[2F(x1)-1][2F(x2)-1], 若x1 F|X(1)|,|X(2)|(x1,x2)=F(x1)[2F(x2)-F(x1)]-F(-x1)[2F(x2)-F(-x1)] -[F(-x2)]2+[F(-x2)]2=[2F(x1)-1][2F(x2)-1], 则F|X(1)|,|X(2)|(x1,x2)=F|X(1)|(x1)F|X(2)|(x2),即|X(1)|与|X(2)|相互独立. (iii)对x≥0 对x<0 则|X1|-|X2|~L(1),同理有:|X(1)|-|X(2)|~L(1). 致谢非常感谢各审稿专家给予的宝贵意见.3 样本容量为2的标准拉普拉斯分布次序统计量的性质
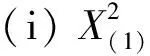
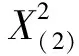
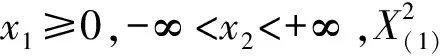
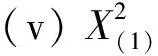

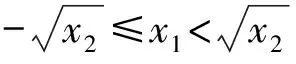
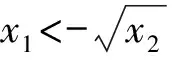
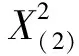
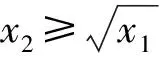
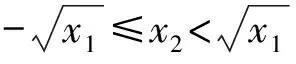
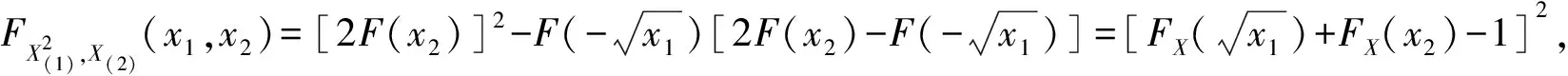
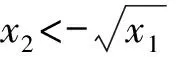
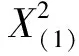
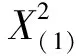
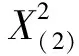
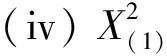
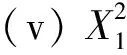
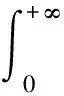
4 结 论