椭圆曲线y2=3px(x2+2)的正整数点

万 飞，邓娅容，汪 越

数学与应用数学

椭圆曲线y2=3px(x2+2)的正整数点

万 飞，邓娅容，汪 越

（红河学院 教师教育学院，云南 蒙自 661199）

椭圆曲线；正整数点；同余；Legendre符号

1 引言及相关结论

椭圆曲线的整数点是数论中很重要的问题[1-9]。对于形如

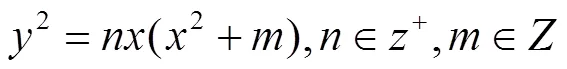
的椭圆曲线方程，当=2时，变为

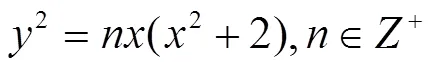
的整数点问题，目前还没有相关结论，本文主要讨论椭圆曲线(2)的正整数点情况。

2 重要引理

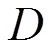
3 相关定理

4 定理证明

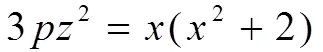
表1 (3)式分解的8种情形

下面分别讨论这8种情形下椭圆曲线(2)的整数点的情况。

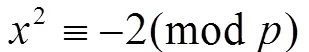
则(4)式不成立。因此，情形Ⅰ不成立，即椭圆曲线(2)无正整数点。

情形Ⅱ 仿情形I证明知该情形不成立，即椭圆曲线(2)无正整数点。

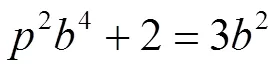
情形Ⅴ 仿情形Ⅰ证明知该情形不成立，即椭圆曲线(2)无正整数点。

情形Ⅵ 仿情形Ⅰ证明知该情形不成立，即椭圆曲线(2)无正整数点。

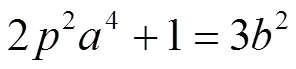
即

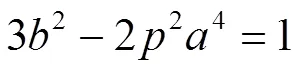
由引理1知，方程(6)至多有1组正整数解，故椭圆曲线(2)至多有1个正整数点。

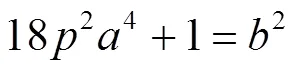
即

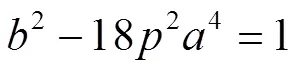
由引理2知，方程(7)至多有1组正整数解，故椭圆曲线(2)至多有1个正整数点。

综上所述，定理得证。

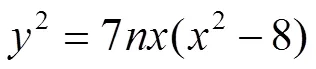
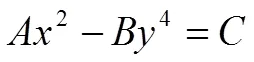
Integer Points of Elliptic Curves2=3(2+2)

WAN Fei, DENG Ya-rong, WANG Yue

(College of Teachers Education, Honghe University, Mengzi 661199, China)

It was proved that the elliptic curve in title at most has two positive integer points with the help of the properties ofcongruence and Legendre symbol.

elliptic curve; positive integral point; congruence; Legendre symbol

O156

A

1009-9115(2021)06-0001-02

10.3969/j.issn.1009-9115.2021.06.001

红河学院大学生科技创新项目（SC1943），云南省教育厅科学研究基金项目（2019J1182）

2020-12-16

2021-05-04

万飞（1969-），女，云南建水人，副教授，研究方向为数学教育及初等数论。

（责任编辑、校对：赵光峰）