一种三角网格模型的轮廓生成方法

秦 宇，曹 力,2，吴 垚，李 琳,2

一种三角网格模型的轮廓生成方法

秦 宇1，曹 力1,2，吴 垚1，李 琳1,2

(1. 合肥工业大学计算机与信息学院，安徽 合肥 230601； 2.工业安全与应急技术安徽省重点实验室，安徽 合肥 230009)

从三维网格模型中提取轮廓信息是一个具有挑战性的过程。现有的方法一般是基于局部形状特征分析，如曲面的曲率和相邻面法向之间的夹角，但其特性通常对模型中的局部特征变化敏感。为了解决这个问题，提出一种基于三维形状几何近似的轮廓提取方法。利用完善的变分几何分割算法来得到一套完整的描述性特征曲线，首先基于变分几何近似方法划分模型为若干分片；其次提取所有分片的内部特征曲线，并过滤较短的特征曲线；然后将分片的边界曲线平滑化；最后合并分片边界曲线与特征曲线，并延伸曲线得到闭合的轮廓。该方法的优点是：在几何近似的基础上结合特征提取方法，使轮廓能够体现三维形状的全局结构。通过在各类网格模型上进行实验和比较表明，该方法在提取模型轮廓的正确性和完整性方面优于现有方法。

网格模型处理；变分形状近似；几何分割；轮廓线提取；特征提取

三维模型的轮廓抽象地描述了物体的几何形状，是计算机图形学应用中的一个重要因素，被广泛应用于几何处理中，例如形状设计[1]、表面重构[2]、形状编辑[3]。在逆向工程领域，三维物体在数字化过程中不可避免地会产生一些缺陷，如噪声、表面细节缺失、某些区域过于光滑等，降低了三维模型的适用性。DEY和WANG[4]提出了一种获取高质量三维物体的表面模型的方法，该方法从扫描的点云数据中提取特征曲线，并使用其重建更好的表面。但由于点云中存在噪声、离群点以及数据和拓扑信息缺失等问题，很难提供可靠的特征曲线。因此，获得高质量重建的模型显得尤为重要[2]。

从点云或多边形网格中提取特征曲线，在许多文献中得到了广泛的研究。在大多数研究中，提取特征线的几何标准是曲率张量或曲率导数[5-7]。通过局部或全局方式拟合网格顶点，然后估算曲率来提取特征曲线。YANG和ZHENG[8]提出了一种新的曲率张量估计算法，通过分段曲面插值在三角形网格上进行曲率张量估计，比曲面拟合的方法有更精确的结果。WEINKAUF和GÜNTHER[9]利用曲面的主曲率提取拓扑骨架，并且引入分界持久性概念以正确区分显著特征边缘和非显著特征边缘。TORRENTE等[10]将Hough变换扩展到三维形状领域，用代数方法识别三维网格上的小特征。LAI等[11]引入特征敏感度量识别特征，并使用数学形态学的思想对特征进一步分类。KIM等[12]采用张量投票理论特征提取，求解顶点的法向投票张量矩阵的特征值，再根据特征值将特征分类为角点、锐边、边界。除此之外，一些研究中还引入了二面角[13]、离散微分几何[14]、移动最小二乘[15]，避免了估计曲率张量或曲率导数时巨大的计算量。

上述研究专注于特征提取技术，且未生成连续的特征曲线，无法直接用于模型的重建工作。通常将离散的特征曲线连接为连通封闭的轮廓线需要用户的交互。LU等[16]提出一种自动检测特征网络的方法，结合曲线曲率和曲面拟合误差提取特征曲线，然后对曲线扩展生成连通的模型轮廓。CAO等[17]通过曲率估算的方法提取特征曲线，保留明显和较长的曲线进一步生成模型分片布局。对于高质量的网格，这种基于局部曲面分析的方法能提取有效的特征曲线。但在含有噪声的网格上、稀疏的网格上曲面拟合产生的误差大，估算的微分量不准确，一些重要的特征曲线常常被忽略。在含有尖锐边缘的CAD模型上，用光滑的曲面拟合也是不合理的。网格分割方法为轮廓线的获取提供了另一种解决方案：从分割结果中提取分片的边界作为轮廓线。NIESER等[18]扩展平面区域划分网格，然后将区域边界作为特征边、区域相交点作为特征点生成网格的特征图。变分形状近似(variational shape approximation，VSA)方法基于平面近似将网格划分为多个区域[19]。在此基础上，WU和KOBBELT[20]扩展了变分形状近似技术，引入球体、柱体作为近似的基本元素进行划分。YAN等[21-22]进一步扩展为二次曲面近似，依据二次曲面拟合误差进行划分。VSA底层采用的度量距离是一个非微分性质的量，加上聚类的约束，使得提取的特征线不会随着噪声的增多而有所改变，在特征提取上更加鲁棒，能处理很多特殊情况下的网格。

本文提出了一种结合几何近似和曲面曲率的方法，可以从网格模型中生成最佳的描述性轮廓。该方法是基于完善的变分几何划分策略。其首先利用VSA算法获得分片集合，分片边界作为初始轮廓。然后，采用特征检测方法提取分片内部特征曲线，过滤，获得内部细节特征。最后通过平滑、合并、扩展等步骤优化曲线，得到最终的轮廓。与现有的方法相比，该方法可以生成一组完整的特征轮廓，将其进一步平滑后转换为输入模型的完整轮廓线。

1 轮廓生成流程

本文方法输入一组三角形组成的网格模型，通过一系列操作步骤，输出描述三维模型形状特征的高质量轮廓线。轮廓线提取流程如图1所示，首先基于VSA方法，将原始网格模型划分为若干分片，并使用最优划分方案，根据输入网格模型的复杂程度确定分片的个数，降低VSA方法随机划分带来的弊端。保留每个分片的边界曲线作为初始轮廓等待进一步连接。其次，对于网格的每一个分片，采用特征检测方法识别内部区域的局部特征，生成内部特征线，借助过滤步骤，去除大量短小的特征曲线。然后，提出边缘平滑方法，处理分片的所有边缘曲线。最后，将边界曲线和每个分片内部的局部特征曲线进行合并，扩展某些尚未连通的曲线，从而生成一个封闭的轮廓。一个连接良好的轮廓，可以用来重建光滑的网格模型以供进一步使用。

如图1所示，轮廓信息生成的核心步骤为：

步骤1. 对网格模型进行VSA划分；

步骤2. 对分片内部进行特征提取并过滤；

步骤3. 对分片边缘平滑处理，提取边缘轮廓；

步骤4. 合并步骤2和3获取轮廓曲线；

步骤5. 检查轮廓的完整性，扩展不连通曲线；

步骤6. 输出轮廓数据。

图1 本文方法流程图

2 轮廓线生成过程

2.1 分片信息提取

VSA方法[19]基于聚类的思想将网格划分为若干片，不需要计算局部微分系数。但是VSA方法在划分过程中随机选取种子点，可使得划分结果不理想。种子点数量过少，丢失过多几何信息，最终提取的轮廓无法描述原模型的形状。种子点数量过多，增加了轮廓的复杂度。因此，在原有的VSA方法的基础上，本文采用优化策略进行合理的分片划分。

(1) 合并分片。通过VSA操作获得分片集。由于种子初始位置的随机性，一些平坦的区域可能会被分割成多个分片，增加不必要的轮廓。因此，需要将这些分片合并为一个。通过计算相邻分片间的2,1距离值衡量分片之间的相似程度，确定是否需要合并。如果2分片的代理间2,1的距离值小于阈值，则需要合并分片。其中，阈值的选择依据文献[23]所提出的种子点优化采样算法，即

其中，R为需要被扩展的分片；P为分片的代理；分片为R内的顶点；()为顶点的法向量；为第个分片的法向量。

(2) 划分分片。一些局部变化明显的区域，需要更多的分片来表示，对于每个VSA划分分片的结果，计算分片中所有三角形法向量的方差。设置一个阈值，如果方差大于阈值，则表明该区域特征变化明显，需要将该分片进行再次划分，直到满足阈值。否则，由少数VSA分块得到的边界曲线不能很好地生成重建结果，甚至可能无法重建。

(3) 边界区域处理。一些三角形由于顶点的平均法线而被错误地聚类到邻接分片中。因此，需要检查每个分片的边界区域的三角形。通过计算这些三角形和附近分片之间的2,1距离，以找到正确的分类(见第1节的步骤1)。

2.2 特征提取和过滤

仅获得分片的边界作为轮廓是不够的，为了获得更详细的模型结构特征，还需要进一步对分片内部的特征线进行提取。对于一般的网格模型，边界信息和小特征都会导致其微分系数值的变化。这些也是现有解决方案中确定小特征的标准。大多数特征感知方法采用微分系数对分片法线进行过滤，从而去除小特征。特征保持方法的关键步骤是识别不同分片的小特征。本文方法采用了一种改进的特征提取方法[6]，基于局部曲面拟合技术估算顶点曲率，获得特征点。对于分片的每一个顶点，用一个三阶多项式方程拟合顶点的小曲面。根据曲率极值捕获特征点，然后连接成特征曲线。特征曲线表示为一组有序的特征点，即={0,1,2,···,v}。

由于特征提取过程中产生了大量的特征线，有些特征强度非常小，表现为短小的特征曲线，这些特征曲线不仅会增加计算量，还会导致最终无法提取到完整的轮廓线。因此，需要将这些曲线滤除。与DFN (detecting feature networks)方法[17]的过滤方案相同，定义尺度无关量来度量特征线的强度。通过对设定阈值过滤掉强度不高的特征线，从而保留显著、较长的特征线。通常通过模型的复杂度和局部特征来设置合理的阈值。如图2所示，大量短小的特征线被过滤掉(见第1节中的步骤2)。

2.3 边界平滑

在分片划分的过程中，VSA划分的分片可能会存在锯齿边界，这是由于边界由三角形的边缘组成所引起的。对于具有小特征的网格，这种情况更为严重。多数情况下，小特征的分布是稀疏的和局部连通的。为了解决该问题，本文提出了一种边缘平滑方法，如图3所示。其主要步骤如下：

步骤1.根据分片所包含的三角形数量对所有分片进行排序。

步骤2. 从包含三角形数量最少的分片开始，搜索其边界附近三角形，如果存在另外一个分片中有2个以上的三角形与该分片中的三角形有相同的边，则该三角形将被合并，然后递归搜索相邻的三角形，直到没有这样的三角形。

步骤3. 通过不断迭代图3(a)和(b)得到光滑的分片边界。

图3 网格细分前后对比((a)网格细分前；(b)网格细分后)

图3需要说明的是：如果初始网格三角面较少，且质量不高(有大量狭长的三角形)，需要进行保边界的细分，变成稠密网格后才能进行处理，否则本文方法流程可能无法给出理想的结果(见第1节中的步骤3)。

2.4 轮廓扩展和合并

上述步骤中的边界和内部特征曲线将继续用来完成特征线合并和延伸的工作。相邻分片之间会存在公共的边界，导致在合并过程中一些边界线段是冗余的。所以有必要去除这些冗余边界，生成简洁的轮廓。

还有一些特征曲线之间互不连通，需要进行处理，将其与附近的曲线连接。针对这种情况，本文提出了一种新的解决方案。扩展曲线的端点生成候选点，其来自于端点附近的网格顶点。在搜索候选点的过程中，首先添加端点的1邻域的顶点，如果1邻域中未满足条件的顶点，进一步扩大搜索范围，在本文中设置最大搜索邻域为3。对于这些候选点，本文设计了一个权重函数来选择最合适的候选点作为新的端点。将选定的端点逐渐添加到线段，直到所有线段都相互连通或者候选点集为空，形成闭合的轮廓，即

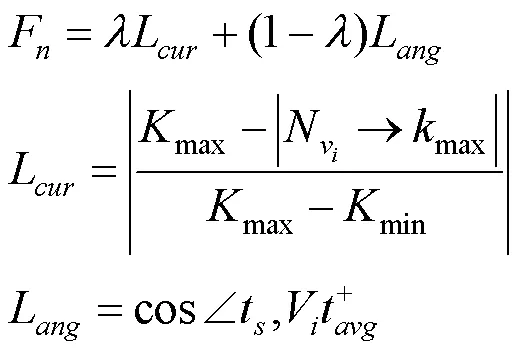
其中，权重函数包含2项，为候选点的曲率影响因子，max和min分别为候选集中每个顶点的最大主曲率值中的最大值和最小值。|N→max|为候选顶点的最大主曲率，其范围为[0,1]。为角度影响因子，即候选顶点和端点的方向与特征线方向之间的角度，其范围为[-1,1]。用于控制不同网格两项的权重(见第1节中的步骤4和5)。

经过以上各步操作，最终可以获得三维模型的简洁、闭合的轮廓表达。

3 结果与讨论

用实验结果来验证本文提出方法的有效性。相关的实验在如下配置的台式机上完成：主频为4.4 GHz的CPU，16 GB内存，1080Ti显卡。程序通过C++编程实现。其中，三维模型的数据均来自于文献[24]中提供的模型数据库。

3.1 对比试验

实验选取了多个网格模型在该方法上进行测试。如图4所示，Torch模型中按钮区域的短特征线由于其长度较短、曲率变化不明显，在使用谷脊线提取的方法处理时会被过滤掉，但本文方法可以被保留。这是由于本文方法基于VSA的划分结果，在生成轮廓线的过程中可以结合模型的全局信息进行处理。

同样，在Vase模型的轮廓线提取中，由于底部的曲率变化不明显，在这些位置的轮廓线缺乏特殊描述，会在特征过滤的步骤中被移除。FCNE (feature curve network extraction)方法[16]虽然可以连通所有提取的特征线，给出比DFN[17]方法更好的结果。但是FCNE的方法也未得到完整的轮廓，如图5(b)所示。而本文的方法利用分片收集模型的全局结构信息，可以得到更完整的轮廓，如图5(c)所示。

为了进一步验证本文方法，实验采用ZHUANG等[25]提出的重建方法对每个模型生成的轮廓重建曲面。该方法输入模型的轮廓线信息即可自动构建三角网格模型。图6～9给出了每个模型的原始网格、基于VSA方法划分后的结果、本文方法生成的轮廓线和使用文献[25]算法重建后的网格曲面。结果表明，本文方法可以获得较优的VSA划分结果，再结合其他优化步骤进一步生成完整、简洁的轮廓线，利用生成的轮廓线可以重建出光滑的曲面。

图4 Torch模型的轮廓线

图5 Vase模型的轮廓线((a)原始网格；(b) FCNE方法生成的轮廓线；(c)本文方法生成的轮廓线)

图6 Block模型的轮廓及处理中间结果((a)原始网格；(b) VSA分割结果；(c)轮廓线；(d)重建模型)

图7 Joint模型的轮廓及处理中间结果((a)原始网格；(b) VSA分割结果；(c)轮廓线；(d)重建模型)

图8 Torch 模型的轮廓表达及中间处理结果((a)原始网格；(b) VSA分割结果；(c)轮廓线；(d)重建模型)

图9 Vase模型的轮廓及处理中间结果((a)原始网格；(b) VSA分割结果；(c)轮廓线；(d)重建模型)

3.2 对比分析

FCNE[16]和FDN[17]方法与本文的研究密切相关，为了分析本文方法生成的轮廓线的性能，实验将本文方法与这2种方法进行比较。实验选取多个模型，并分别用DFN、FCNE和本文方法生成轮廓线，然后利用生成的轮廓线重建模型表面。一般来说，重建结果更好的轮廓线被认为是性能较好的轮廓线。因此，通过比较重建后的曲面来分析轮廓线的性能。豪斯多夫(Hausdorff)距离[26]描述了重建后的模型与原始模型的最大误差。豪斯多夫距离常被用来度量重建结果的好坏。距离越小代表重建效果越好。表1给出了测试模型在3种方法上生成的轮廓线重建后的评估数据，表1中，本文方法与FCNE方法相比，总体上可以减少5%的重构误差；对于FanDisk和Vase模型，甚至可以减少18%以上的误差。本文提出的方法也可以处理一些不能用DFN和FCNE处理的模型，在表1中，N.A.对应的方法无法完成模型重建。从这些模型的实验中，可以看出，本文方法提取的轮廓线的整体质量优于这2种方法。这是因为DFN和FCNE方法的基础是谷脊线提取[6]，通过微分量估计计算特征线的方法应用在特征轮廓的生成中有一定的缺陷。首先提取的特征是少量的，由于特征轮廓曲线相较于提取的特征曲线还是比较多的，DFN和FCNE方法需要延伸的部分很多，延伸是一种基于规则的操作，其准确性不能保证，延伸的越深其结果的可靠性越无法保证。其次，谷脊线方法提取的特征线中并没有太多描述曲面信息的曲线，这部分信息的丢失自然会导致描述的重建网格时信息不充足，重建的网格质量比较差。

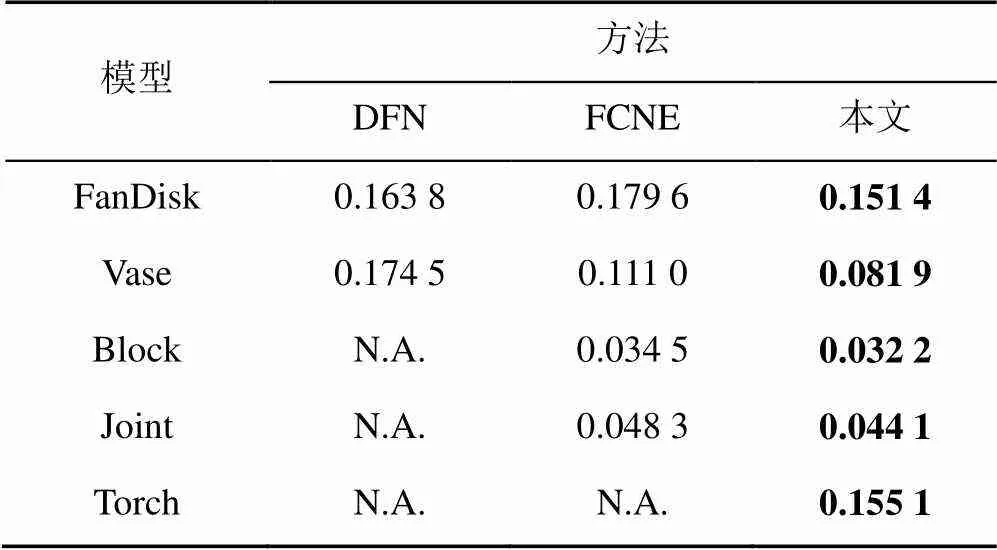
表1 不同方法的重建结果Hausdorff距离

注：N.A.表示无法完成模型重建

3.3 方法的局限性

对于某些类型的网格模型，例如，具有许多不对称特征的模型，用本文方法尚不能很好地获得其轮廓。在这些情况下，因为很难平衡计算成本与精度，所以分片数量的选择是一个难题。为此，在后续的工作中，将进一步改进所提出的方法，以便在保持良好结果的同时，减少分片数量。

4 总 结

在轮廓线提取工作中，本文提出了一种基于几何近似的三角网格模型轮廓生成方法。该方法利用一个成熟的变分几何分割算法来获得一组用于提供初步轮廓信息的分片，并对每个分片进一步分析，得到相对较小的局部特征曲线。该方案的优点是，可靠的特征过滤机制可以固有地融入到几何近似步骤中，从而产生能够捕获三维全局形状结构的描述性轮廓。通过在各种网格模型的实验表明，该方法在提取轮廓曲线的正确性和完整性方面要比现有的一些方法更好。对于具有扫描曲面或复杂结构的网格，能生成较好的轮廓，从而在重建过程中产生较小的重建误差。完整的三维模型的轮廓曲线可以用来完成各种应用，如重网格划分、简化、渲染等。本文方法可以为这些应用提供高质量的轮廓信息，进而更好地表达原始网格。

[1] XU B X, CHANG W, SHEFFER A, et al. True2Form: 3D curve networks from 2D sketches via selective regularization[J]. ACM Transactions on Graphics, 2014, 33(4): 131:1-131:13.

[2] CAO Y H, NAN L L, WONKA P. Curve networks for surface reconstruction[EB/OL]. [2021-02-07]. https://arxiv.org/abs/ 1603.08753.

[3] GAL R, SORKINE O, MITRA N J, et al. iWIRES[J]. ACM Transactions on Graphics, 2009, 28(3): 1-10.

[4] DEY T K, WANG L. Voronoi-based feature curves extraction for sampled singular surfaces[J]. Computers & Graphics, 2013, 37(6): 659-668.

[5] STYLIANOU G, FARIN G. Crest lines for surface segmentation and flattening[J]. IEEE Transactions on Visualization and Computer Graphics, 2004, 10(5): 536-544.

[6] YOSHIZAWA S, BELYAEV A, SEIDEL H P. Fast and robust detection of crest lines on meshes[C]//2005 ACM Symposium on Solid and Physical Modeling - SPM '05. New York: ACM Press, 2005: 227-232.

[7] ARHID K, UNIVERSITY H S, ZAKANI F, et al. An efficient hierarchical 3D mesh segmentation using negative curvature and dihedral angle[J]. International Journal of Intelligent Engineering and Systems, 2017, 10(5): 143-152.

[8] YANG X N, ZHENG J M. Curvature tensor computation by piecewise surface interpolation[J]. Computer-Aided Design, 2013, 45(12): 1639-1650.

[9] WEINKAUF T, GÜNTHER D. Separatrix persistence: extraction of salient edges on surfaces using topological methods[J]. Computer Graphics Forum, 2009, 28(5): 1519-1528.

[10] TORRENTE M L, BIASOTTI S, FALCIDIENO B. Recognition of feature curves on 3D shapes using an algebraic approach to Hough transforms[J]. Pattern Recognition, 2018, 73: 111-130.

[11] LAI Y K, ZHOU Q Y, HU S M, et al. Robust feature classification and editing[J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(1): 34-45.

[12] KIM H S, CHOI H K, LEE K H. Feature detection of triangular meshes based on tensor voting theory[J]. Computer-Aided Design, 2009, 41(1): 47-58.

[13] ARHID K, UNIVERSITY H S, ZAKANI F, et al. An efficient hierarchical 3D mesh segmentation using negative curvature and dihedral angle[J]. International Journal of Intelligent Engineering and Systems, 2017, 10(5): 143-152.

[14] HILDEBRANDT K, POLTHIER K, WARDETZKY M. Smooth feature lines on surface meshes[C]//The 3rd Eurographics Symposium on Geometry Processing. New York: ACM Press, 2005: 85

[15] KIM S K, KIM C H. Finding ridges and valleys in a discrete surface using a modified MLS approximation[J]. Computer-Aided Design, 2006, 38(2): 173-180.

[16] LU Z D, GUO J W, XIAO J, et al. Feature curve network extraction via quadric surface fitting[C]//2019 Pacific Conference on Computer Graphics and Applications (PG 2019). Goslar: The Eurographics Association, 2019: 47-52.

[17] CAO Y H, YAN D M, WONKA P. Patch layout generation by detecting feature networks[J]. Computers & Graphics, 2015, 46: 275-282.

[18] NIESER M, SCHULZ C, POLTHIER K. Patch layout from feature graphs[J]. Computer-Aided Design, 2010, 42(3): 213-220.

[19] COHEN-STEINER D, ALLIEZ P, DESBRUN M. Variational shape approximation[J]. ACM Transactions on Graphics, 2004, 23(3): 905-914.

[20] WU J H, KOBBELT L. Structure recovery via hybrid variational surface approximation[J]. Computer Graphics Forum, 2005, 24(3): 277-284.

[21] YAN D M, LIU Y, WANG W P. Quadric surface extraction by variational shape approximation[C]//The 4th International Conference on Geometric Modeling and Processing - GMP 2006. Heidelberg: Springer, 2006: 73-86.

[22] YAN D M, WANG W P, LIU Y, et al. Variational mesh segmentation via quadric surface fitting[J]. Computer-Aided Design, 2012, 44(11): 1072-1082.

[23] 徐源廷. 面向三角网格分割的几何处理技术研究[D]. 合肥: 合肥工业大学, 2020.

XU Y T. Research on geometry processing technology for triangular mesh segmentation[D]. Hefei: Hefei University of Technology, 2020 (in Chinese).

[24] GAO X F, SHEN H X, PANOZZO D. Feature preserving octree-based hexahedral meshing[J]. Computer Graphics Forum, 2019, 38(5): 135-149.

[25] ZHUANG Y X, ZOU M, CARR N, et al. A general and efficient method for finding cycles in 3D curve networks[J]. ACM Transactions on Graphics, 2013, 32(6): 180: 1-180: 10.

[26] DUBUISSON M P, JAIN A K. A modified Hausdorff distance for object matching[C]//The 12th International Conference on Pattern Recognition. New York: IEEE Press, 1994: 566-568.

A novel wire frame generation for triangle meshes

QIN Yu1, CAO Li1,2, WU Yao1, LI Lin1,2

(1. School of Computer and Information, Hefei University of Technology, Hefei Anhui 230601, China; 2. Anhui Province Key Laboratory of Industry Safety and Emergency Technology, Hefei Anhui 230009, China)

Extracting wire frame from 3D models is a challenge. Existing methods are typically based on the analysis of local shape properties, such as surface curvatures and angles between faces, which are generally sensitive to small features in the model. In order to solve this problem, we proposed a wire frame extraction method based on geometric approximation of 3D shapes. This method employed a well-established variational geometric segmentation algorithm to derive a complete set of descriptive feature curves. Firstly, the model was divided into several patches based on the variational geometry approximation method. Secondly, the internal characteristic curves of all patches were extracted, and the short characteristic curves were filtered. Then, the boundary curves of patches were smoothed. Finally, the patch boundary curves and characteristic curves were merged, and the closed wireframe network was obtained by extending the curves. The advantage of the proposed method was that descriptive wire frames can capture the global structures of the 3D shapes using a reliable feature filtering mechanism that was inherently incorporated in the geometric approximation step. Experiments on various kinds of meshes have been carried out and the results demonstrate that our method is superior to existing approaches in terms of correctness and completeness of the extracted wire frame.

mesh model processing; variational shape approximation; geometric segmentation; wire frame extraction; feature extraction

TP 391

10.11996/JG.j.2095-302X.2021060963

A

2095-302X(2021)06-0963-07

2021-04-13；

2021-05-21

国家自然科学基金项目(61602146)；安徽省自然基金青年基金资助项目(1708085QF137)；中国高校基本科研业务费专项资金资助项目(JZ2019YYPY0011)

秦 宇(1996–)，女，山西吕梁人，硕士研究生。主要研究方向为计算机图形学。E-mail：18856329235@163.com

曹 力(1982–)，男，安徽芜湖人，副教授，博士。主要研究方向为计算机图形学、几何分析等。E-mail：lcao@hfut.edu.cn

13 April，2021；

21 May，2021

National Natural Science Foundation of China (61602146);Youth Fund of Anhui Provincial Natural Science Foundation (1708085QF137); Fundamental Research Funds for the Central Universities (JZ2019YYPY0011)

QIN Yu (1996–), female, master student. Her main research interest covers computer graphics. E-mail：18856329235@163.com

CAO Li (1982–), male, associate professor, Ph.D. His main research interests cover computer graphics, geometric analysis. E-mail：lcao@hfut.edu.cn