基于加权直方图均衡化彩色图像增强仿真
2022-01-22王利娟
王利娟,常 霞,任 旺
(1.北方民族大学宁夏智能信息与大数据处理重点实验室,宁夏 银川 750021;2.北方民族大学数学与信息科学学院,宁夏 银川 750021;3.北方民族大学算机科学与工程学院,宁夏 银川 750021)
1 引言
高质量的彩色数字图像对于描述图像信息内容具有重要价值。在不良的捕获环境下,会捕获到一些低对比度、色偏严重的低质量图像。利用增强算法改善图像质量成为重中之重。图像增强技术在获取视觉情报信息、目标追踪和航空航天遥感等领域具有重要的价值。
直方图均衡化算法[1]是众所周知的传统空域类图像增强方法。HE算法一方面旨在输出图像的直方图呈现均匀的分布,另一方面旨在输出图像的亮度保持。近年来,对于HE算法提出了大量的改进算法。算法基于均衡化思想可以被划分为全局直方图均衡与局部直方图均衡两大类。基于全局类算法是通过加法减法等变换算法对图像灰度值直接调整。Lin等人[2]提出的平均加权直方图均衡化算法(AvHeq)很好的保持了图像的亮度信息,但是AvHeq算法并未考虑图像的色彩信息。基于局部类算法则利用图像局部均值、方差、梯度等信息进行局它的原始直方图呈现两端趋势,灰度级大多占部区域增强,并以单个像素的邻域灰度分布信息设计映射函数,使得邻域不断的逐像素平移。Ganesan等人[3]提出利用子块完全重叠来增强人像面部的细节内容,算法有效地减少了局部光照的不良影响,但算法中“块效应”影响难以消除。Minjie等人通过局部加权平滑算法和局部最小值算法将直方图自适应地分割成背景和目标两个区域的直方图[4],算法有效地避免了过增强现象,但该算法计算量大且无法平衡输入图像和输出图像之间的亮度信息。Zou等人[5]提出一种增强图像亮度的同时,校正图像颜色信息的白平衡算法;以及徐义春等人[6]提出了保持色调不变的图像增强算法,算法在图像的纹理细节恢复方面均未取得满意的效果。Veluchamy等人[7]基于修正直方图分布函数的均衡化思想提出利用伽马函数来修正累积分布函数,史学超等人基于直方图剪切的思想提出改进限制对比度自适应直方图均衡化算法(CLAHE)[8],算法有效地避免了伪像的产生。但无论是修正函数或剪切函数的选择都极其复杂。其它包括结合其它算法的直方图算法,高古学等人提出了CLAHE与带色彩恢复因子的多尺度Retinex的图像增强算法[9],但输出结果中依然存在局部信息丢失现象。
上述图像增强方法[2-9]在提高图像对比度的同时,往往会造成颜色信息的丢失。为改善图像清晰度的同时且能大幅度的提高图像的色彩信息。论文提出一种基于加权直方图均衡化算法。算法利用灰度级的分布特点构造新的均衡化映射函数,为减少传统HE算法中第一次均衡之后出现的灰度级合并造成的部分细节信息丢失问题,利用不同的映射函数对直方图进行二次映射。通过颜色幅度饱和度信息的拉伸,弥补亮度通道均衡化之后出现的去饱和和色彩损失现象。
2 加权直方图均衡化实现彩色图像增强
2.1 颜色幅度拉伸
输入RGB格式的彩色图像。图像可以被表示为
I(u,v)={R(u,v),G(u,v),B(u,v)}
(1)
其中(u,v)表示像素的位置坐标,并且满足u=1,…,U,v=1,…,V。(U,V)是图像的宽度和高度。对于对比度低、有色偏的彩色降质图像,据中间区域。颜色幅度拉伸通常被用作一种预处理技术,可以恢复因不良环境而丢失的部分信息。将R,G和B三个通道信息尽可能的拉伸到最大范围。拉伸公式如下所示:
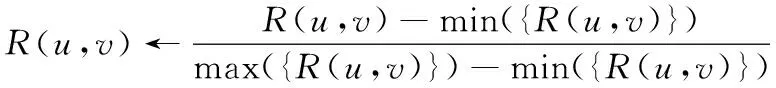
(2)
其中min({R(u,v)})和max({R(u,v)})表示各个通道中像素的最小值和最大值。
2.2 颜色空间转换
RGB模型是基于红、绿、蓝三基色的混合叠加而呈现的色彩。R,G和B之间的平衡因增强算法极易被破坏。HSV色彩空间是一种基于人类视觉效应的更加直观的六棱椎体模型。色度(H)会随着角度的变化而变化,饱和度(S)的大小决定了图像颜色接近光谱的程度,明度信息(V)信息与图像的亮度保持有着直接的联系。对于图像处理和模式识别,HSV空间在视觉特性上比其它颜色空间更具有直观性[10]。论文将RGB格式的图像转至HSV空间中,并对V通道和S通道进行算法增强,转换函数[11]
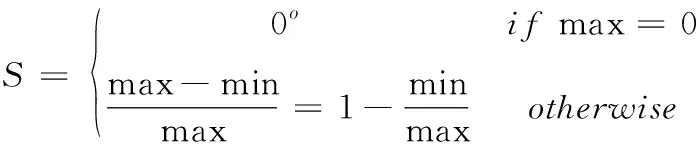
(3)
V=max
(4)
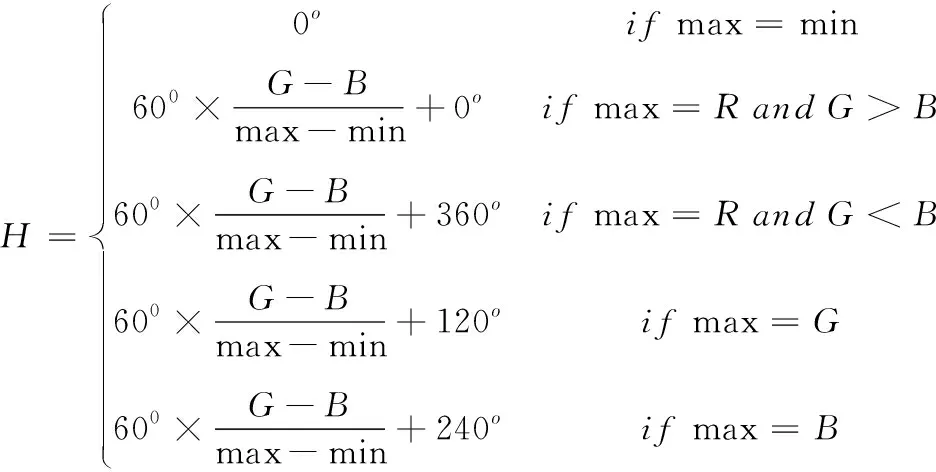
(5)
其中,max和min表示R,G,B的最大值和最小值。
2.3 加权直方图均衡化算法设计
图像的直方图能显示图像像素值的分布特征,通过对直方图的优化,可以使得输出图像的直方图既保持输入图像直方图形状又均匀分布在整个区间。直方图均衡化算法通过对灰度级的非线性映射来提高个数较少的灰度级,削减个数较多的灰度级,使得输出图像的直方图呈现均匀分布。算法具体步骤如下[12]:
1)统计输入图像直方图
p(i)=n(i)/N
(6)
式中,图像的灰度级为i,像素总数为N,n(i)是第i灰度级的像素总数。
2)计算累计直方图分布

(7)
3)利用灰度映射函数,计算变换后的灰度值
T(k)=round(C(k))
J(u,v)=T(k)
(8)
其中round(.)表示取整,J(u,v)=T(k)表示映射函数。实验结果如图1所示。
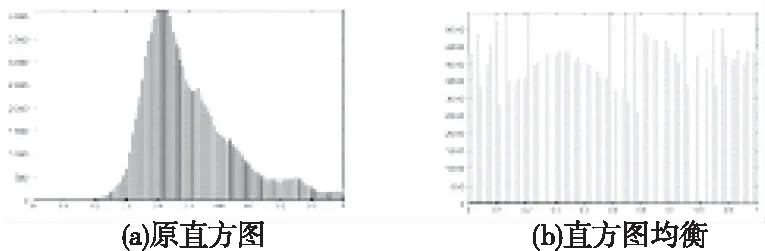
图1 直方图均衡化结果
由HE的算法原理和图1可知,HE算法的图像增强是从连续到离散的近似计算过程。算法存在缺陷:1)量化误差,即两个以上不同灰度的像素值在映射之后会输出为相同的灰度级,造成灰阶合并和图像部分信息丢失情况;2)像素满足离散分布,对图像信息不区分,输出的直方图无法保持输入直方图的形状,如图1b)所示,灰度级均匀分布在整个区间,却并未保持原始形状。这也是造成图像信息丢失的关键因素。
针对信息丢失、灰阶合并现象,算法通过权重将灰度级重新组合成加权和的形式以平衡图像的能量,设计出一种新的映射函数。
(i)←β×h(i)+ω×max(h(i))
0<ω<1,ω+β=1
(9)
其中,h(i),和max{h(i)}分别是灰度级和最大灰度级,i=0,1,…L-1。当h(i)←(L-1),有如下表达式
(i)max←(ω+β)×(L-1),=L-1
(10)
由(10)可得,ω+β=1能确保输出的灰度级始终保持在[0L-1]范围内,尽可能的恢复更多的图像信息。该映射函数可实现高灰度级变小,低灰度级变大,输出图像的直方图呈均匀分的目的,有效地增强了图像的对比度并避免了局部灰度级过增强现象。对于某些急剧变化的灰度级,依然存在部分堆叠造成信息丢失现象。观察直方图的变化可以检测出均衡化后丢失的灰度级。故需对直方图进行重新映射,首先指定一个集合Ω来储存非空的灰度级。公式定义如下
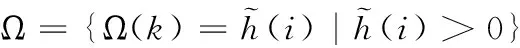
(11)
其中,Ω((k)将存储加权直方图均衡化后生成的非空灰度级的数目,且满足k=1,2,…kmax。依据映射函数将其再次映射到[0L-1]区间内,该映射函数为
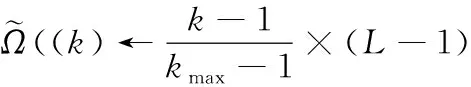
(12)
综上所述,V通道直方图经过二次映射前后输出图像的直方图如图2所示。图2b)显示直方图加权均衡之后依然存在部分灰度级分布不均匀现象。再次映射后,直方图既保持原始直方图形状又均匀的分布在[0 1]范围内。得到的增强结果为
Vout(u,v)=T((i),Ω(k))
(13)
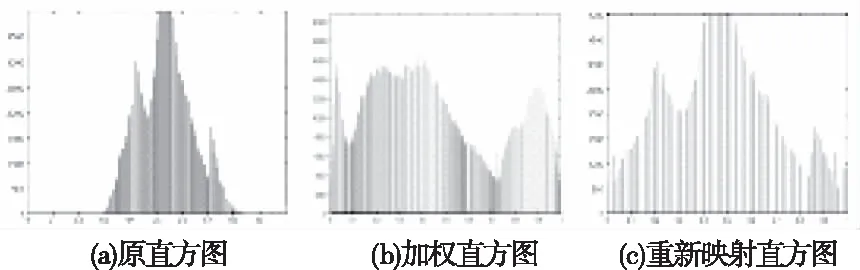
图2 二次映射前后直方图结果
2.4 黄金分割算法
根据等式(9)可知,权重的选择对增强结果有着至关重要的影响。黄金分割算法[13]是一种快速的搜索算法。将图像信息熵H和亮度信息作为搜索依据,故搜索权重的目标函数为

(14)

(15)

1)输入源图像Iin(u,v),计算平均亮度值Iin,m;
2)输入黄金分割点ρ=0.618,迭代初始值为α1=eps,α2=1-eps;
3)误差范围记为Δα=α1-α2,并确定一个较小的精确度值τ→ε=10-4;
4)计算α1,α2所对应的目标函数J1,J2;
5)当满足Δα>τ,J1>J2
更新区间端点α2←α1+ρ×Δα,并将J2记为目标函数
反之,更新端点α1←α1+(1-ρ)×Δα,同时J1记为目标函数
6)不断更新区间端点α1,α2和目标函数J1,J2,直到满足Δα<τ结束搜索;
7)返回并计算权值ω=0.5×(α1+α2),β=1-ω
2.5 饱和度最大化
基于HSV空间的亮度图像被增强后,不可避免的会出现去饱和或颜色损失现象。这是亮度通道增强过程中固有的缺陷。这个缺陷可以在RGB和HSV的变换过程中显示出来[14]。依据等式(3)和 (4),当增强V通道时,图像灰度级会趋于L-1,存在V=max{R,G,B}→(L-1),或者表示成如下形式
R(u,v)←(L-1),G(u,v)←(L-1),B(u,v)←(L-1)
(16)
根据等式(17),最小饱和度如下所示

(17)
针对这一缺陷,需要扩展饱和度至最大范围。饱和度越大,图像的颜色类型越丰富。故有
Sout(u,v)=max{Sin(u,v)}.
(18)
最终输出的增强图像为
[R(u,v),G(u,v),B(u,v)]
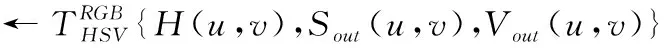
(19)
3 算法实现
针对传统HE算法中存在细节信息丢失和灰阶段合并造成伪影的不足,提出改进HE均衡化过程中的映射函数。具体算法过程如图3所示。
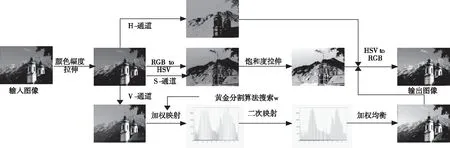
图3 改进算法的实验过程整个图像增强的算法步骤如下所示,
1)输入RGB格式的原图像Iin(u,v),分别对其R,G和B通道进行颜色幅度拉伸;
2)将步骤1得到的拉伸后的图像进转换至HSV空间,得到V通道图像V(u,v)和S通道图像S(u,v);
3)对于步骤2中得到的V(u,v)图像的直方图进行加权均衡化算法操作,其中的权值参数获取是利用黄金分割算法迭代获得,最终得到新的V通道图像Vout(u,v);
4)对步骤2得到S(u,v)图像最大化拉伸算法操作,得到新的S通道图像Sout(u,v);
5)对步骤3和步骤4得到的最终的Vout(u,v)和Sout(u,v)图像作颜色空间逆变换至RGB空间。
4 实验结果分析
将本文算法与HE,CLAHE,AvHeq和文献[5]中算法在Matlab2018b的PC端进行对比实验。实验结果如图4-7所示。图像4和5分别命名为“earth”和“bridge”。图6和图7分别被命名为“126007”和“5096”,原图像来自BSD500数据集中。
4.1 主观分析
图4(a)-(f)显示,b)HE算法的直方图出现了灰阶合并现象,增强结果的部分细节丢失。c)CLAHE算法的色彩和岩石纹理细节恢复不自然,对应的直方图也未能保持原始形状。d)AvHeq算法亮度信息恢复不足,直方图结果存在部分堆叠。e)文献[5]的算法结果对比度较低且模糊,直方图显示图像灰度级集中在中间位置,灰度信息丢失严重。f)改进算法岩石的明亮程度和清晰程度均有很大改善,尤其岩石中间的颜色信息恢复明显,直方图结果既保持了原始形状又均匀的分布于整个区间。在图5(a)-(f)中,改进算法的去雾效果和颜色信息恢复结果均取得了更加满意的效果,尤其是灯笼和树木的颜色以及汉字的信息。对应的直方图结果较其它算法也是最满意的。图6(b)-(f)显示,HE和CLAHE算法均会导致天空颜色出现些许失真。AvHeq和文献[5]算法倒是使得天空的颜色信息有所恢复,但无法很好地保持图像的亮度。改进算法的亮度和对比度均很大程度得到改善,天空和山脊的颜色信息恢复明显。虽然对应直方图结果显示部分灰度级并未均匀分布,但主观视觉效果较其它算法是最满意的。
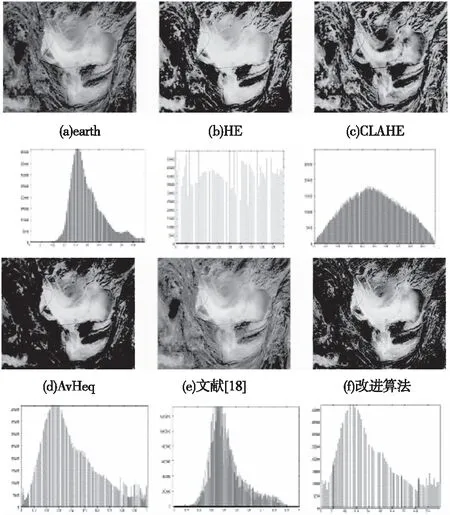
图4 不同算法对图像”earth”的增强结果
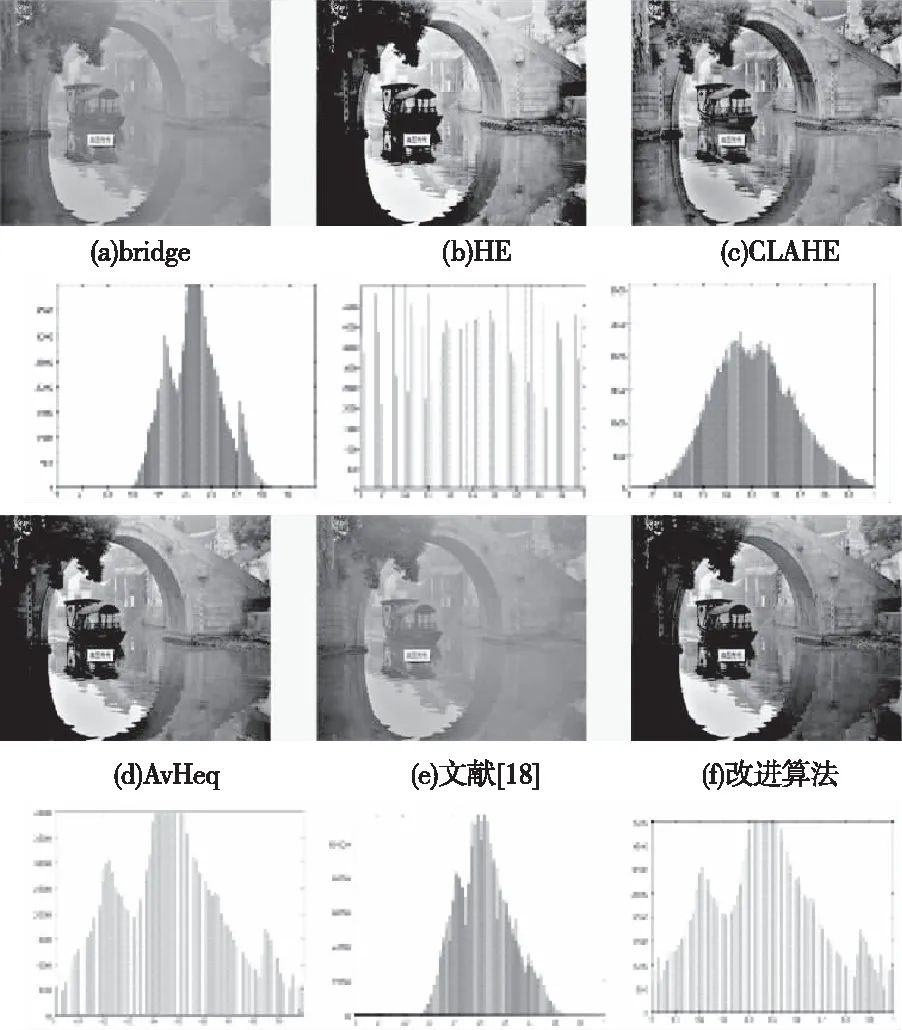
图5 不同算法对图像”bridge”的增强结果
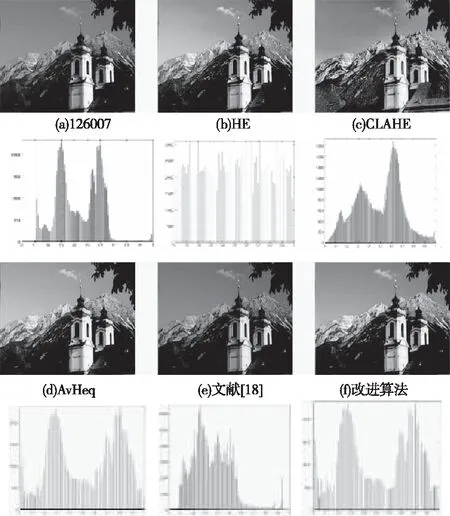
图6 不同算法对图像”126007”的增强结果

图7 不同算法对图像”5096”的增强结果
4.2 客观分析
增强图像的结果除了主观上的表达,还需要使用一些测量数据进行评估,包括熵,图像清晰度[15]和平均梯度[16]。
图像熵是一种基于概率的强度分布统计信息,可以描述图像信息量,如式(15)所示。图像清晰度(Tenengrad梯度)反映了图像的清晰程度。公式如下
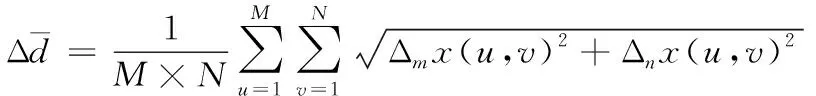
(20)
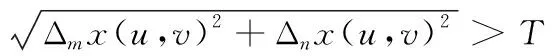
(21)
其中,T为阈值,Δmx(u,v) 和Δnx(u,v)分别是像素(u,v)水平与垂直方向上像素之间的差异。
平均梯度描述了图像细节的对比度和纹理的变化。公式如下
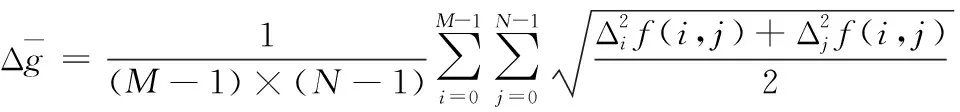
(22)
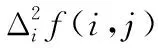
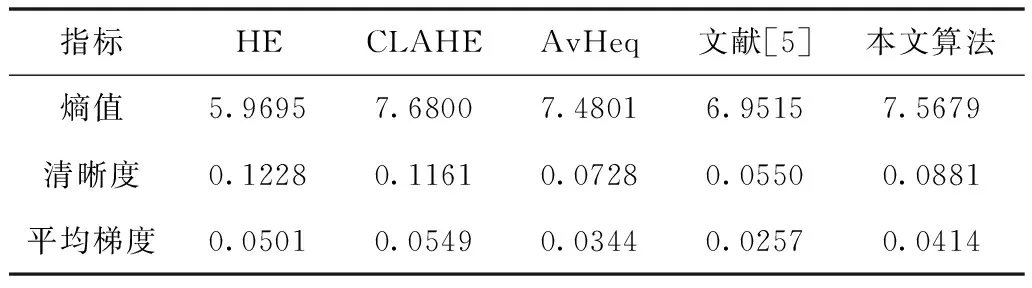
表1 图4的客观评价指标结果
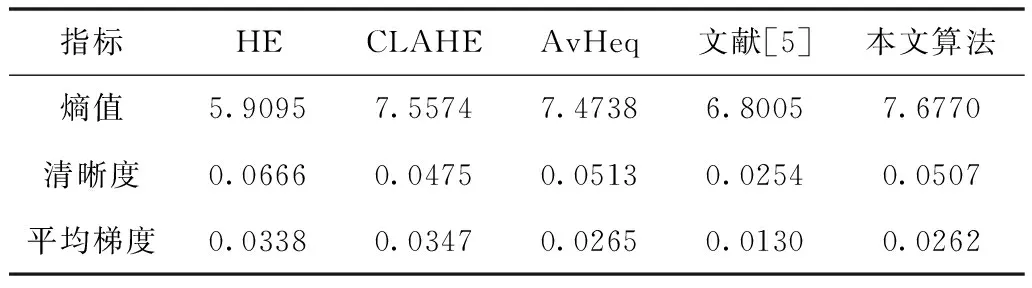
表2 图5的客观评价指标结果

表3 图6的客观评价指标结果

表4 图7的客观评价指标结果
分析表1-4可知,HE和CLAHE算法实验结果提高了图像的清晰度和平均梯度,但局部细节丢失严重以及局部信息出现过增强现象,采取加权直方图均衡可以有效抑制HE和CLAHE算法的不足。AvHeq算法的直方图结果既均匀的分布在整个区间又保持了原始形状,但缺少对颜色信息的恢复,饱和度拉伸可以弥补颜色信息,所以整体视觉效果不如改进算法。文献[5]算法结果对比度低,所以图像熵值、清晰度和平均梯度不如改进算法。总之,实验表明,改进算法的评价指标整体上相对较高,对比度较高,视觉效果清晰;颜色信息和局部细节信息恢复较为明显。这意味着改进算法克服了细节信息和颜色信息丢失的缺点,对于图像亮度保持和颜色信息恢复较其它算法更为有效。
4 结束语
为解决输出图像亮度保持和颜色信息恢复不足的问题,提出一种加权HE的彩色图像增强算法。实验结果表明:①依据图像灰度级分布特点,利用改进的映射函数对图像的灰度级进行重新映射,对于场景图像具有较好的增强效果;②仿真结果显示,改进算法的增强结果较其它算法在增强图像对比度和亮度的同时实现了颜色保真效果;③熵值、清晰度和平均梯度客观指标优于其它算法。算法弥补了图像低灰度区域处理后出现的亮度过度缺陷,并能有效地恢复颜色信息,体现了改进算法的优势。对于构建更简单的目标函数以及引入其它智能搜索算法的进一步研究提供了依据。
