基于转子结构优化的永磁同步电机噪声研究*

2022-01-22王淑旺储轶群

汽车技术 2022年1期

王淑旺储轶群

（合肥工业大学，合肥 230009）

主题词：永磁同步电机径向电磁力波固有模态响应曲面法电磁噪声

1 前言

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）因其结构简单、效率高、功率密度高、调速范围宽等特性，广泛应用于新能源汽车。同时，其噪声也成为新能源汽车噪声的主要来源。电机噪声按产生机理可分为机械噪声、通风噪声和电磁振动噪声，其中电磁振动噪声为主要噪声源。

目前，国内外学者从结构上优化电机电磁噪声的方法主要集中于定子结构优化，但其对电机性能的影响较大，综合考虑电磁噪声和电机性能时，转子结构优化是改善电机电磁振动噪声的重要思路。现有研究在转子结构优化方面主要集中于对转矩脉动和齿槽转矩的抑制，较少从优化径向电磁力的角度考虑。部分学者研究了电机振动噪声的来源：文献[4]研究了不同电机的振动噪声问题，提出电磁激振力是电机振动噪声产生的主要原因；文献[5]指出永磁同步电机的振动噪声问题主要源于径向力波引起的电磁振动，并提出在一定条件下可通过麦克斯韦应力张量法获得径向电磁力波；文献[6]通过分析电机的各噪声阶次，提出低阶次谐波和永磁体磁场相互作用产生的噪声是电机总体噪声的主要贡献量。在此基础上，有学者从电机定、转子结构优化的角度对电机电磁振动噪声优化展开了研究：文献[7]、文献[8]通过耦合的多物理场方法研究了转子表面辅助槽对电磁噪声的影响；文献[9]、文献[10]研究了定、转子槽对径向电磁力波的影响以及槽口的位置和槽型对特定阶次径向电磁力波的影响；文献[11]通过优化转子的磁障结构改善电机的电磁激振力，从而优化电机的电磁噪声。

本文以一台额定功率为60 kW 的车载永磁同步电机为研究对象，首先分析电机特定转速段噪声问题的产生机理，在定子结构优化对改善电机噪声的作用有限且可能恶化电机性能的情况下，提出在转子外表面开设辅助槽的转子结构优化方法，通过对径向电磁力波的有限元仿真验证优化效果，并利用曲面响应法分析得到辅助槽参数对优化目标的影响程度，从而得到最佳优化方案，最后通过样机试验验证优化方案的有效性，为永磁同步电机的电磁振动噪声优化提供参考。

2 径向电磁力分析

永磁同步电机在运行时，由转子励磁和定子电流的激励通过气隙磁导波在气隙中调制出一系列转速、级数、大小均不同的磁场，从而在定子表面产生随时间和空间不断变化的麦克斯韦力。麦克斯韦力切向分量产生电磁转矩和转矩脉动，径向分量称为径向电磁力波，径向电磁力波远大于切向分量，是电机噪声及振动的主要来源，因此本文只针对径向电磁力进行分析。

由麦克斯韦定律，定子表面单位面积上的径向电磁力瞬时值可表示为：

式中，()为气隙磁密；=4π×10H/m为真空磁导率；为该处相位角；为时间。

忽略气隙磁场饱和，则气隙磁密为：

式中，(,)为气隙磁势；(,)为气隙磁导。

永磁同步电机正常运行时，气隙磁势主要由基波合成磁势、定子谐波磁势和转子谐波磁势组成：

式中，()为基波合成磁势；f()为定子绕组次谐波磁势；f()为转子绕组次谐波磁势；、ω为相对于定子的基波旋转角速度和转子次谐波角速度；、、为相应的初始相位角。

由于式（3）已经考虑了转子凸极的影响，求解磁导时，只需求解定子外表面不开槽时的气隙磁导，此时气隙中的磁导为：

式中，为定子开槽且气隙长度为时的气隙平均磁导幅值；λ为次谐波磁导幅值；为定子开槽数。

将式（3）、式（4）代入式（2），得到气隙磁密为：

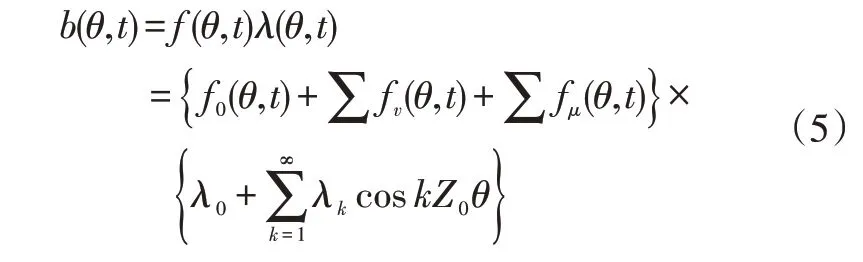
整数槽永磁同步电机定子绕组谐波次数为：

转子永磁磁场的谐波次数为：

式中，=0,±1,±2,…、=0,1,2,3,…为谐波磁场次数，正、负分别表示谐波磁场正、反向旋转；为电机极对数。

式（5）展开后，重点关注转子的主极磁场次谐波和定子绕组产生的电枢磁场次谐波作用产生的径向电磁力波阶数和对应的频率：

式中，=0,1,2,3,...；为电网频率。

由式（8）和式（9）可知，径向电磁力波阶次是电机极数的整数倍，而且由于定子铁心的径向形变量与力波幅值成正比，与力波空间阶次的4 次方成反比，因此低阶次径向力波是电磁振动和噪声的主要来源，可以忽略相对高阶的电磁力波。由式（8）和式（9）计算可知，力波最低阶次为0阶，其次为8阶，因此，针对本文研究对象，关注的影响电机电磁振动噪声的电磁力波阶次为0 阶，8阶及以上阶次电磁力波对电机电磁振动噪声的影响可以忽略。

3 电磁仿真分析和模态试验

永磁同步电机难以用数值分析方法获得径向电磁力，为了得到所研究样机径向电磁力波的分布规律，利用有限元法在Maxwell 中建立二维电磁模型，主要参数如表1所示，模型如图1所示。

表1 电机模型参数

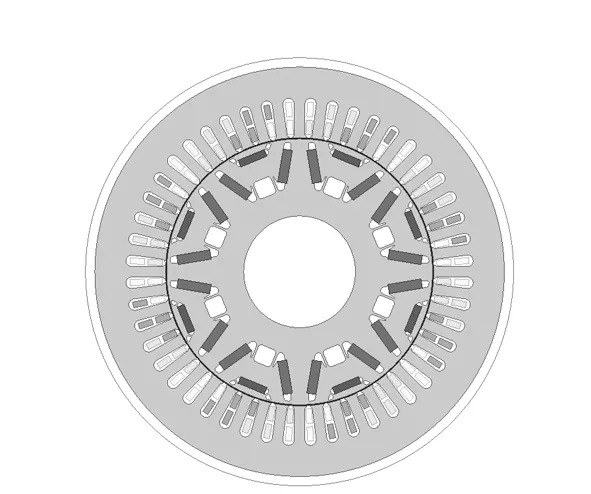
图1 电机二维电磁仿真模型

通过仿真可以得到电机在转速为7 000 r/min 时的电流及其角度，在此基础上对气隙中的电磁力进行仿真，时长为1 个电周期，得到径向电磁力波的时空分布如图2 所示。为了得到不同空间阶次和频率阶次电磁力的幅值，在MATLAB 中，通过二维傅里叶变换对径向电磁力波进行时空分解，得到各空间阶次电磁力在不同频率段的分布，其结果可作为后文多因素试验的响应值。

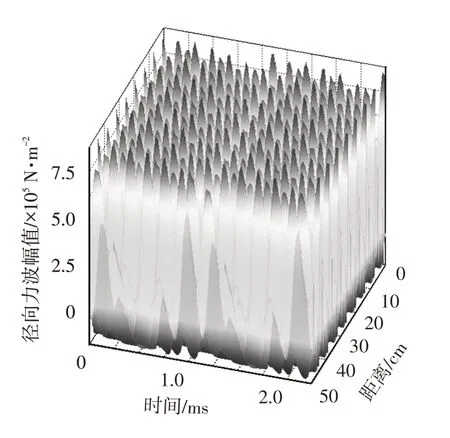
图2 径向电磁力波的时空二维分布

通过模态测试分析可以对电机模态参数进行识别，确定其动态特性并分析可能存在的问题。径向电磁力波与电机发生共振需满足2个条件：径向电磁力波阶次与定子模态阶数一致；径向电磁力波频率与该阶次的定子模态频率接近。因此，在确定径向电磁力波的空间和频率特性后，还需得到电机的模态特性。

由本文研究样机的近场噪声测试结果可知，电机在7 000 r/min处出现噪声最大值，频率公式为：

式中，为阶次值；为转速。

计算可知，48 阶次噪声峰值处对应的频率为5 600 Hz。

本文选用某公司的测试设备和分析软件，利用锤击法对定子和绕组整体进行模态测试，得到低阶次的电机模态振型和模态频率，其中0阶模态振型如图3所示，0阶模态频率为5 576 Hz，与48阶次噪声峰值对应频率接近，可知空间0阶、频率48阶次电磁力波作用在电机定子上，激起整机0 阶模态，使得局部转速段噪声声压级激增，与理论分析结果吻合。

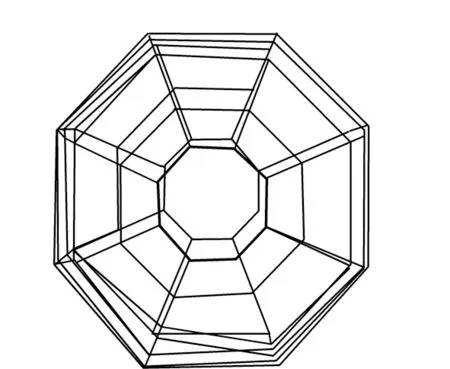
图3 电机的0阶模态振型

4 转子结构优化设计

4.1 优化方案

永磁同步电机的电磁噪声受电磁力波的幅值和电机定、转子结构振动特性的综合影响，在分析电机电磁振动噪声时，可以从这2个角度考虑。电机结构的振动特性与电机材料和结构有关，若改变电机的0阶模态频率使其远离空间0阶电磁力的48倍频率，则需对电机结构进行较大改动，并且会影响电机其他阶次固有频率，从而带来影响电机性能的隐患，因此本文从适当降低径向电磁力波幅值的角度优化电机电磁振动噪声。由式（1）可知，径向电磁力主要取决于气隙磁密，而电机气隙磁密分别与磁势、磁导率成正比，与气隙长度成反比。转子开辅助槽可增大气隙长度，减小气隙磁密的幅值，从而降低径向电磁力波幅值，同时可有效减小电机的磁导，由式（2）知，也使得气隙磁密幅值减小，但同时会影响电机的输出转矩。因此，本文采取在电机转子外表面开设辅助槽的方法来降低电磁噪声，并使用曲面响应法对转子辅助槽尺寸参数进行连续性分析，以确定最佳优化方案。

曲面响应法是一种基于条件参数设计试验并寻找最优结果的方法，对试验得到的数据采用二次回归方程进行拟合，分析并寻求最优参数和最优预测响应值。

为防止转子辅助槽引入谐波影响电机性能，在转子外表面开设对称矩形辅助槽，在尽量不降低电机输出转矩的前提下减小径向电磁力幅值，其分析参数包括槽深、槽宽、夹角，如图4所示，通过对比仿真得到的电机48 阶径向电磁力幅值的大小和变化趋势，选择最优开槽方案。

图4 转子辅助槽尺寸参数

4.2 多因素仿真

综合考虑辅助槽对电机转子强度和电机性能的影响，确定各参数的范围为∈[4°,12°]、∈[0.4,1.2]mm、∈[0.8,1.6]mm，以仿真得到的48 阶径向电磁力波幅值作为评价指标，仿真结果如表2所示。

表2 多因素水平试验结果

根据表2中的数据样本，通过Design-Expert软件得到48阶径向电磁力波幅值的二次多项式回归模型为：

式中，为48 阶径向电磁力波幅值；为双槽角度；为槽深；为槽宽。

根据回归模型的分析结果，采取双变量同时变化的研究方法，利用软件分析各因素的交互效应，得到如图5 所示的三维响应曲面图。由图5a 可知，双槽角度在增加的过程中，电磁力波幅值的变化趋势受槽深影响，双槽角度较小时电磁力波幅值随槽深加深而增大，相反，在双槽角度较大时，电磁力波幅值随槽深加深而减小，由此可得，与槽深相比较，双槽角度对响应值的影响幅度更大。由图5b 可知，双槽角度由4°增大到12°过程中，槽宽越大，电磁力波幅值增幅越大，由此可得，与槽宽相比较，双槽角度对响应值的影响程度更大。由图5c 可知，当槽深较深时，随着槽宽的减小，径向力波幅值增大，响应曲面较为平展，两者之间的交互作用并不明显，对于响应值的影响幅度均较小，因此，槽宽对响应值的影响程度相对于槽深更大。

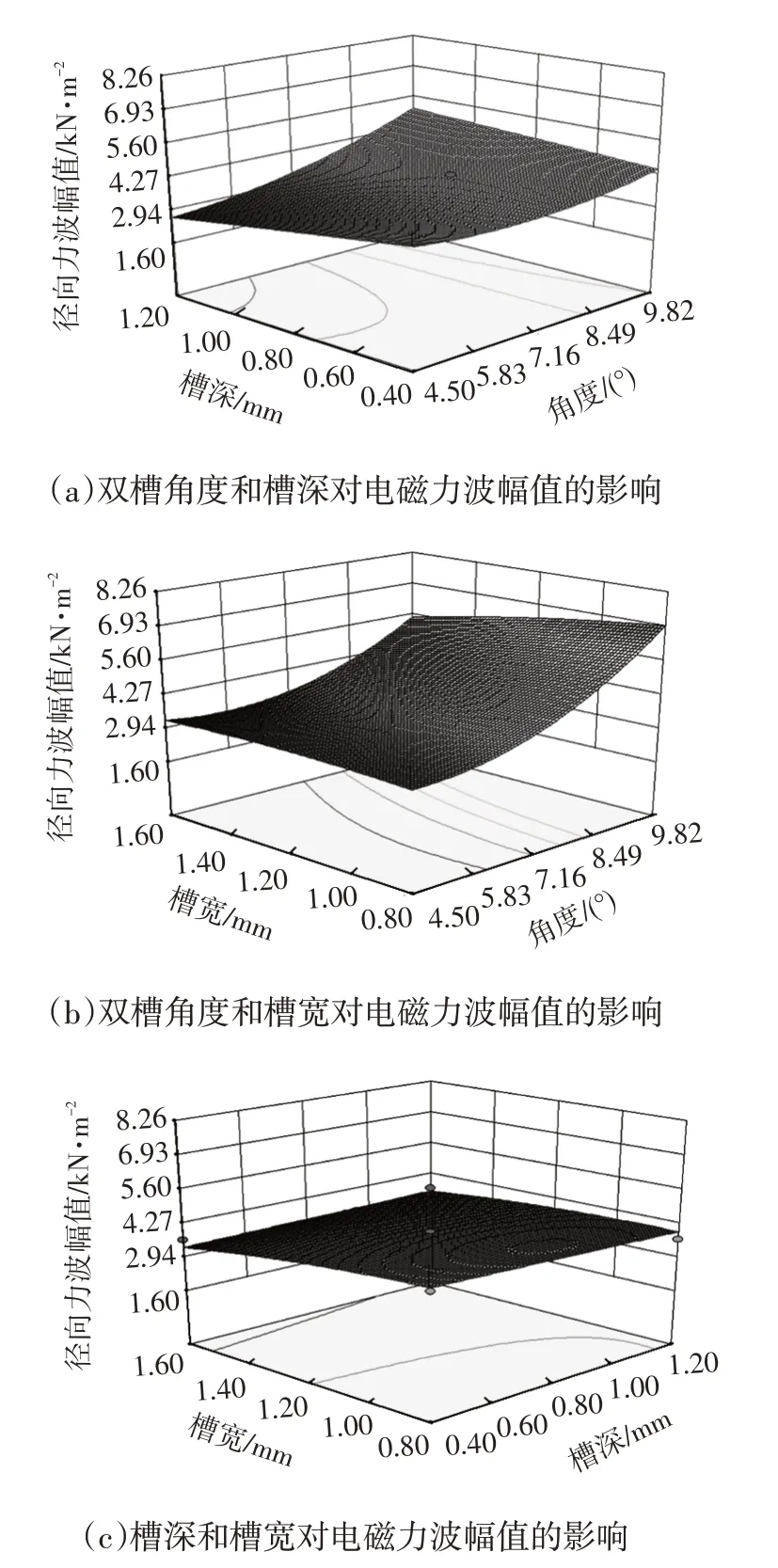
图5 响应曲面交互作用分析

由曲面分析结果可知，为了优化径向电磁力波幅值，应选择较小的双槽角度和槽宽、较大的槽深。利用软件通过曲面响应优化算法得到最佳响应值为双槽角度4°、槽深1.2 mm、槽宽0.8 mm，预测48 阶径向电磁力波幅值响应值为2.298 kN/m。

5 优化前、后电机仿真和试验结果对比

5.1 优化方案仿真对比

基于多因素仿真得到的最优辅助槽参数，建立优化前、后的电机模型，利用Maxwell 仿真软件分析优化前、后电机的性能，结果如图6所示。

图6 优化前、后电机性能对比

由图6a 可知，径向气隙磁密基波幅值几乎不变，结构优化后电机的性能几乎没有受到影响。由图6b可知，优化后电机的输出转矩平均值从170.39 N·m下降到169.14 N·m，输出性能没有显著变化。由图6c 和图6d 可以得到不同空间阶次径向电磁力的不同频率分量对应的径向电磁力波幅值，其中频率为0 的径向电磁力为恒定电磁力，幅值较大但不影响电机的电磁振动噪声，而0 阶电磁力的48 阶径向电磁力波分量是本文关注的电磁力分量，其幅值由优化前的4.540 kN/m下降到2.400 kN/m，降低了47.14%，与多因素仿真得到的最优结果接近，也验证了多因素仿真结果的正确性。

5.2 电机振动噪声试验对比

为验证仿真结果的正确性以及所选优化方案的有效性，在原样机的基础上对电机转子开设辅助槽，其他参数不变，制成优化后样机。

对2台样机在310 N∙m负载下进行匀加速试验，加速段转速为500～11 000 r/min，在相同试验条件下进行振动噪声测试。传感器布点情况如图7所示，试验电机置于试验台架上，在电机轴平面距电机壳体表面0.2 m处布置麦克风，测量电机的近场噪声，电机壳体上布置振动传感器，检测电机壳体振动变化情况。得到优化前、后样机的近场噪声A计权声压级即时频图如图8所示，电机48阶次噪声声压级明显高于其他阶次，优化后48 阶次噪声声压级明显降低。为探究48 阶噪声对整体噪声的贡献量，分别对时频图进行阶次切片分析，结果如图9所示。在7 000 r/min噪声峰值处，总声压级由优化前的96.12 dB(A)下降到了优化后的90.43 dB(A)，48 阶噪声声压级从82.70 dB(A)下降到73.57 dB(A)，48阶噪声对声压级的贡献量从86.04%下降到81.36%，优化效果明显，说明优化后样机能有效改善电机的振动噪声。