控制力约束条件下的喷水推进船鲁棒控制
2022-01-21秦梓荷
曾 宏,秦梓荷,蒋 一,黄 坚
(1.珠海云洲智能科技股份有限公司,广东珠海 519000;2.中国船舶科学研究中心,江苏无锡 214082)
0 引言
近10年来,无人系统的研发得到了极大程度的发展,其中作为核心内容的运动控制问题在控制学界得到了密切的关注。无人艇作为无人驾驶领域的一个重要研究方向,其运动控制的主要研究点包括路径规划、路径跟踪和编队航行等[1-4]。国内外成型的无人艇,大多采用喷水推进滑行艇的基本船体形式,因此重点研究喷水推进无人艇的运动控制具有十分重要的意义。
在控制器设计方面,喷水推进无人艇与常规的螺旋桨推进船舶有一定的差异。与常规固定螺旋桨不同,喷水推进器能为船舶提供矢量推力。通过改变喷口射流方向产生转艏力矩,从而喷水推进船不需要安装舵机,然而推力偏角会产生横向推力,造成纵向推力与转艏力矩具有耦合关系,加大了控制器设计的难度。
针对水面无人艇及无人潜器的运动控制,可使用PID(Proportion Integral Differential)、自适应、反步法和自抗扰等控制方法,且已有大量的研究文献[5-7]。然而,以上文献都只将控制算法执行到控制力/力矩设计的层面,对具体硬件的控制则未加考虑。
要研究喷水推进船的运动控制,首先需要喷水推力大小与主机转速的关系。针对该问题,高双[8]及BA等[9]研究了特定航速下喷水推进器的推力计算问题。然而,虽然喷水推力大小虽然由主机转速直接决定,还受到进水口流速(即船体航速)的影响。喷水推力与转速和航速具有复杂的多元关系,难以通过水动力计算确定不同航速和主机转速下的推力数值。
查阅相关文献可知,目前尚未有学者对喷水推力、主机转速和航速三元关系的计算开展相关研究。为此,本文以解决该问题出发,创建了一种推力-航速-转速三元关系的拟合方法。在此基础上,进一步研究了输入量饱和约束下的喷水推进船航速航向鲁棒控制问题,设计了相应的航速、航向控制律。最后,通过指定航速下的路径跟踪仿真,验证了所提出控制律对航速和航向联合控制时的有效性。
1 喷水推进船舶水面运动模型
船舶的空间运动具有6个自由度,然而在研究水面船舶运动控制的过程中,通常习惯性地忽略船舶的横摇、纵摇和升沉运动。此外,假设船体关于中纵剖面对称(即左右对称),且设随体坐标系的原点位于船体重心处。参考文献[10-11],船舶的水面3自由度运动方程可按如下方式表达:
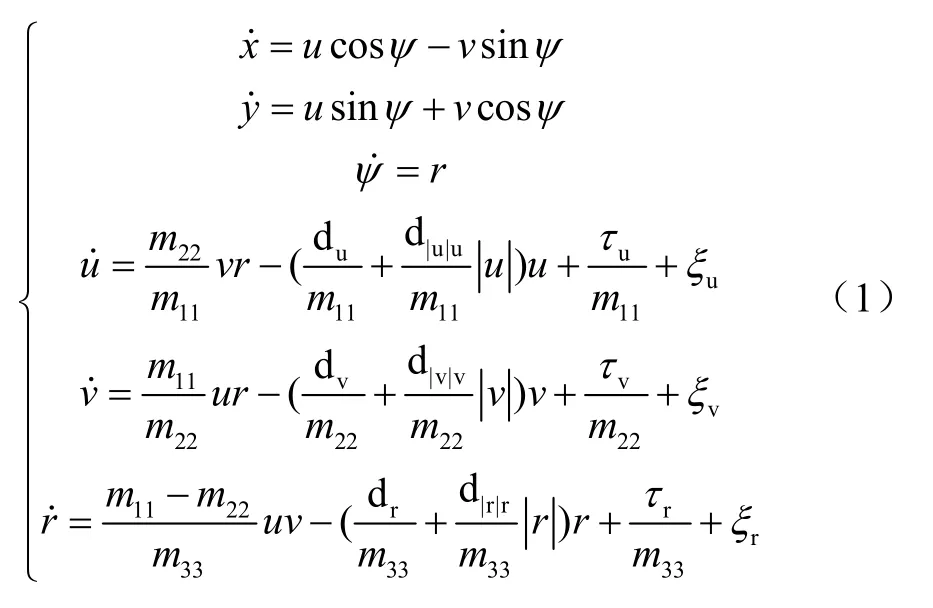
式中:(x,y)为船舶在北东坐标系下的位置;ψ为艏向角;u、v、r分别为船在随体坐标系下前进、横移、转向角的变化速率;转艏力矩τr、纵向推力推力τu、推力τv为主动控制输入量;m11、m22、m33为与船体惯性力相关的运动系数;du、dv、dr、d|u|u、d|v|v和d|r|r等系数与船体运动的流体阻尼相关;ξu、ξv、ξr为环境扰动力在3个自由度的分量,同时符合如下限定条件:外界扰动ξu、ξv、ξr大小有界,且扰动力上界可知,船舶水面运动模型见图1。
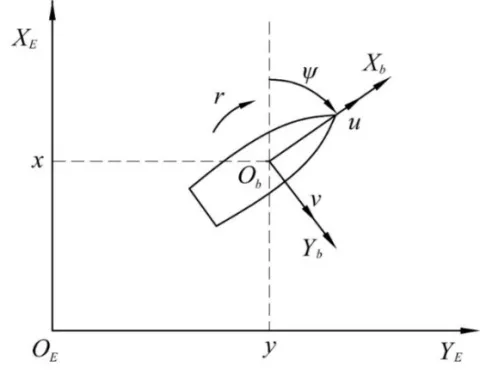
图1 船舶水面运动模型
与螺旋桨动力船舶相比,喷水推进船的控制力形式有明显的区别,且区别在于喷水推进器的矢量推力形式,通过喷水推进器的喷口转动装置代替了传统的舵机。在不考虑倒车斗使用的情况下,喷水推进船的控制力包括喷水推力T和推力偏角产生的转艏力矩N,具体的控制力形式如式(2)所示:

式中:T为喷水推进器的总推力;xT为喷水口到船体重心的纵向距离;δ为喷水推进器的喷口转角,出于简便以及习惯性称呼的原因,在下文的表述中将喷口转角改称为舵角。
式(2)中,虽然喷水推进器有纵向、横向和艏摇3个自由度的控制输入量,但实际上控制输入量只有2个,即推力T和舵角δ,控制系统在本质上仍是欠驱动的。
2 喷水推进器推力函数模型建立
要进行后续的控制律设计和运动控制仿真模拟,首先需要知悉喷水推进器的推力函数关系。对喷水推进器而言,喷水推力大小取决于喷口水流速度,即由泵叶转速n决定(由发动机转速通过减速箱得到,本文中假设减速比为1),但还受船舶航速的影响。
分析可知,喷水推力、船舶航速以及主机功率三者关系具备唯一性。以HJ364型44号叶轮的Hamilton喷水推进器为例,其轴功率Pe和输入转速n之间存在关系Pe= 4 4.5(n/ 1 000)3,且不同轴功率下的航速-推力曲线图谱如图2所示。
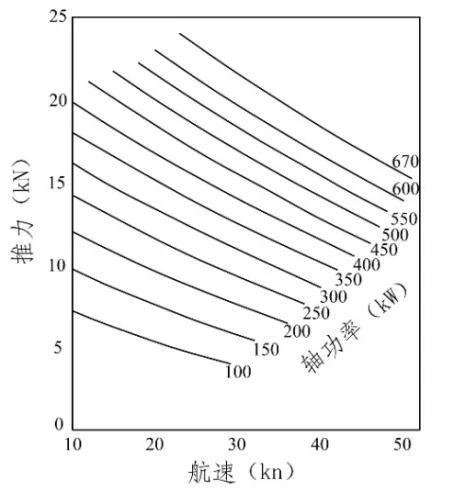
图2 航速-推力曲线图谱
在图2中,功率100 kW、200 kW至600 kW分别对应转速为1.31×103r/min、1.65×103r/min、1.89×103r/min、2.08×103r/min、2.24×103r/min、2.38×103r/min。根据不同航速,提取图2中数据获得如表1所示。
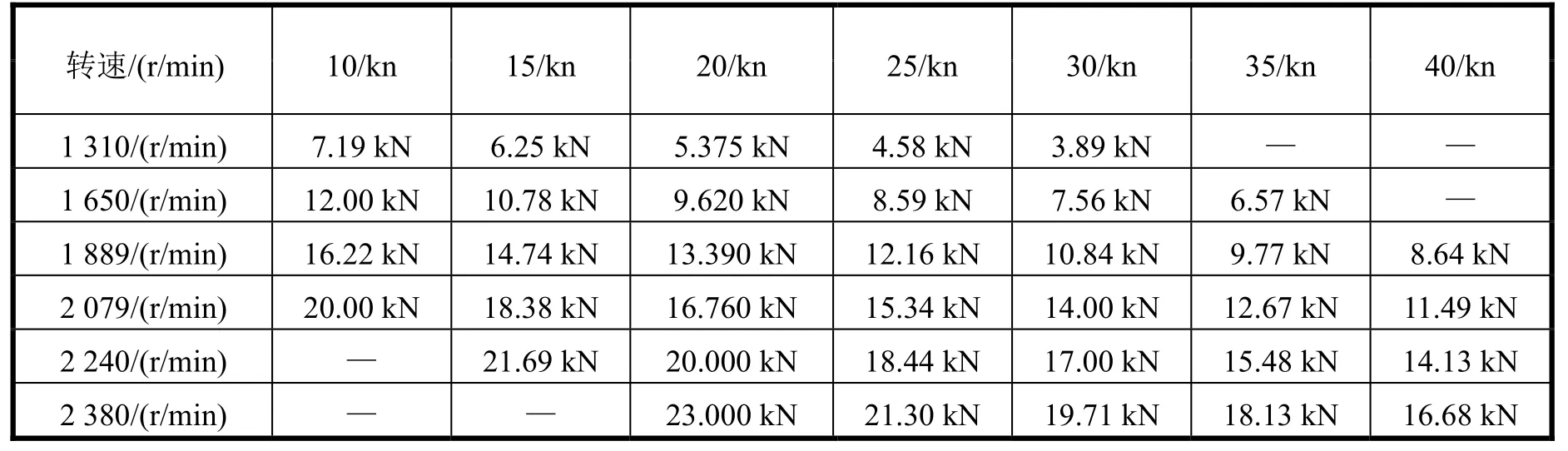
表1 推力-航速-转速关系表
经过反复尝试以及多方案对比,设计得到如下推力函数模型:

式中:f1与f2均为只与vs有关的简单初等函数。
针对表1中的数据,根据航速值重新绘制推力-转速曲线,并按式(3)进行最小二乘拟合,拟合结果如图3所示。

图3 推力-转速特性图谱
图3中实线表示实际值,虚线为拟合曲线。对图3中的函数值进行整理,并对f1与f2分别采用二项式拟合,所得表达式为

结合式(3)与式(5),计算得到表1中各工况下推力的拟合曲线,如图4所示。图4中,实线表示各功率下的实际推力曲线,虚线表示拟合公式的推力计算值,计算值与实际值具有良好的一致性。

图4 拟合推力与实际推力对比图
3 航速航向鲁棒控制算法设计
对于欠驱动的水面船舶而言,通常对航速和航向的控制律进行分离设计,本文中也采用相同的控制器设计策略。考虑到喷水推进器实际推力和外界波浪扰动的不确定性,采用了滑模控制设计航向的鲁棒控制律。航速控制律的设计相对较为简单,不需要使用滑模控制方法。
3.1 航速鲁棒控制律设计
定义期望航速为ud,且航速误差为继而设计如下Lypunov函数:

对式(7)两边求导可得:


根据式(8),设计期望推力控制律为

式中:

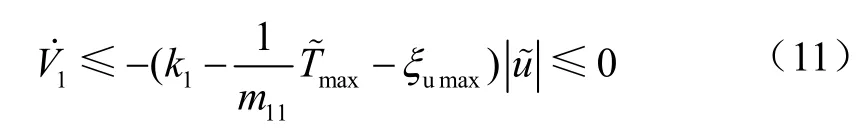
从而Lyapunov函数V1是渐进收敛的,航速误差也将在有限时间内收敛于零。然而式(9)中的符号切换律sgn()有可能导致系统发生抖震现象[12]。为此,改进式(11)的控制律为

式中:
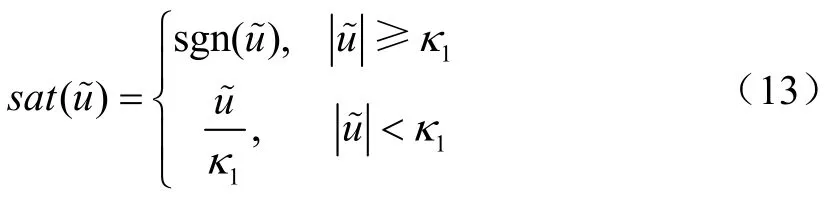
式中:0<κ1<1为切换函数的边界层宽度。
将式(12)代入式(8)可得:

对于式(14),根据的数值大小,可分为2种情况依次讨论。


根据文献[13]可知,V1满足如下的时间函数关系:
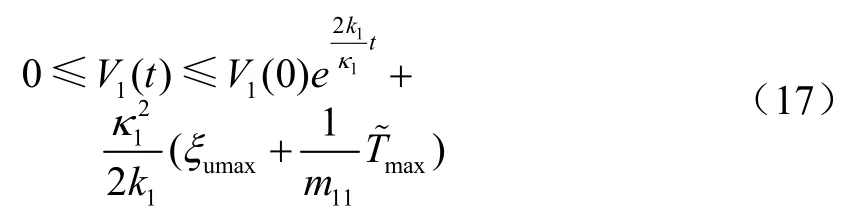
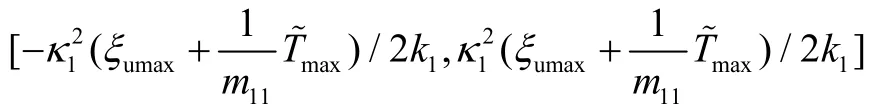
3.2 航向鲁棒控制律
定义为ψ期望艏向角,同时艏向角误差为在此基础上,进一步定义如下了滑模动态面:
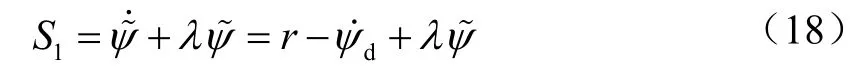
式中:λ为正常数。
定义如下Lyapunov函数:

对上式两边进行求导可得:
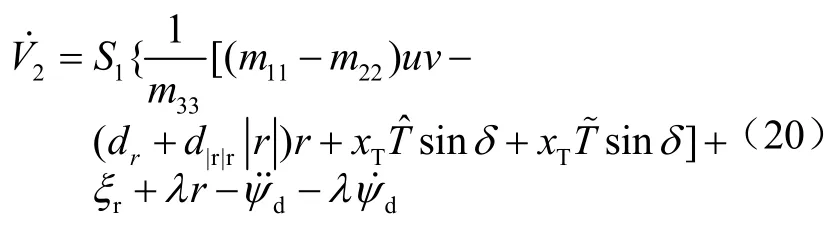
针对上式,设计期望舵角dδ的控制律如下:

其中切换律sat(S1)具有如下格式:
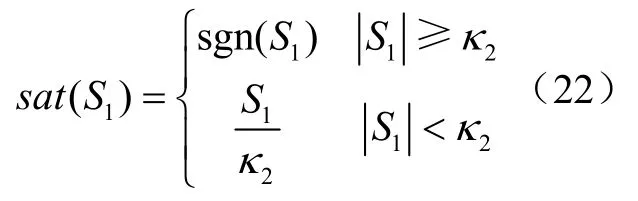
且2κ为小于1的正常数。
将式(21)与式(22)代入式(20)可得:

式中:

同理式(14)至式(17)的证明过程,也可分两种情况推导得到V2满足如下的时间函数关系

则V2将在有限时间内收敛到区间内,通过适当减小κ,并增大k2的取值,可以使滑模面S1逐渐趋近于0。根据滑模理论可知,艏向误差也将趋近于0。
3.3 主机模型和喷口转角模型
喷泵的转速调节模型可以使用发动机调速模型代替。主机模型可以通过一个一阶惯性环节进行描述,则有

式中:˙为主机转速角加速度;为指令转速;Kn为转速上升时间常数。在本文控制器设计过程中,限定主机最大转速为2 300 r/min,最大转速加速度为50。
喷口转动控制可以参照舵机伺服系统,看作一个一阶惯性过程,其运动特性可参照文献[14]表示为如下函数形式:

式中:δ为喷口角;dδ为期望喷口角;Kδ为角度控制增益。喷口角度及角速度存在硬件性能限制:
通过采用式(25)与式(26)的主机和喷口转角模型,结合前文的推力和舵角控制律,即可完成对喷水推进船的航速航向控制与仿真验证。
4 仿真验证与分析
为了验证所提出的控制律能够实现对喷水推进船航速和航向的同时控制,本文进行了指定航速下的路径跟踪控制。仿真中使用Line-of-sight(LOS)导航法进行路径跟踪的艏向规划律设计,具体在文献[15-16]中已经有了详细的论述,本文由于篇幅有限不进行论述。
本文采用文献[17]的无人艇运动模型,通过对水动力系数进行适当整理和转化,可以获得如下的船舶运动参数:m11=2.4×103kg,m22=3.35×103kg,m33=2.49×105kg,du=255 kg/s,d|u|u=50 kg/m,dv=2.92×103kg/s,d|v|v=2.27×103kg/m,dr=1.22×104kg/s,d|r|r=1.2×104kg/rad。
该艇设计水线长5.2 m,排水量1.9 t,喷水口距离船体中心xj=2.01 m,仿真中选取前文中的HJ364喷水推进器,并假设实际推力比估计推力小10%,即T=0.9。控制器中的其他参数取值情况如下:k1=0.8,k2=0.1,κ1=0.05,κ2=0.02,λ=0.25,Kn=20,Kδ=10。
考虑到波浪扰动对航向控制的影响,本文模拟了海浪有义波高1.25m环境下的运动情况。波浪扰动使用文献[18]中的模型进行计算,其 中 ,表示传递函数,且wu、wv、wr均为零均值高斯白噪声,噪声能量谱密度分别为0.01,0.005和0.1。仿真中,u,v,rξ ξ ξ的最大值分别达到了0.1 m/s2、0.04 m/s2和2 (°)/s2,符合实际的航行情况。
无人艇运动初始条件设置为:ψ=135°,u=9 m/s,v=0,r=0,n=1 450 r/min,δ=0°。仿真中设置期望航速ud=10 m/s,路径跟踪及航速航向控制仿真结果如图5~图9所示。图5中虚线表示期望航线,实线为无人艇的实际航行轨迹。

图5 无人艇航行轨迹
图6和图7分别展示了0~200 s时间范围内的无人艇航速和主机转速响应情况。图6中,虚线表示期望航速,实线表示实际航速。在估计推力存在误差的情况下,仍能保证航速达到期望值。

图6 无人艇航速-时间曲线
在图7中,航速在初始阶段有约0.2 m/s的超调量和短期振荡,主要原因是主机转速加速度和一阶操控模型的限制。当航速达到期望值时,无法瞬间下降到适当值,如图8中初始阶段所示。图12中主机转速的小幅振动,原因是为应对外界波浪扰动的补偿量。
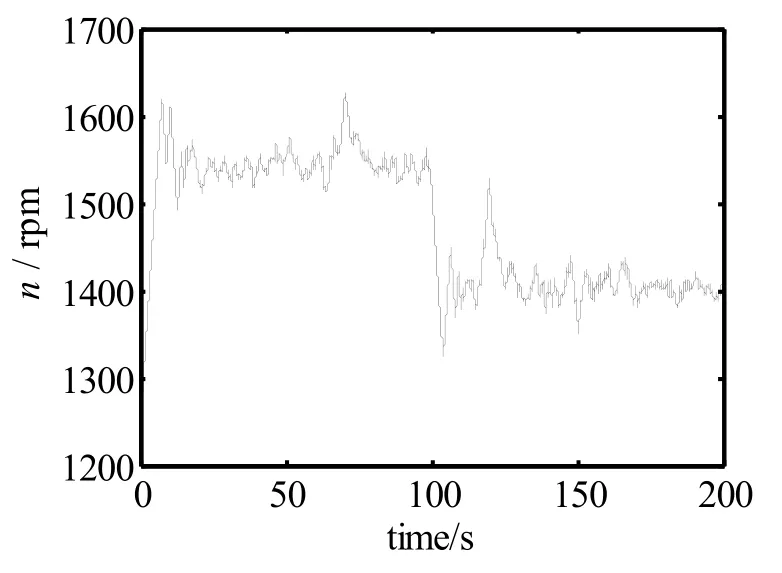
图7 主机转速-时间曲线
图8和图9分别展示了0~200 s时间范围内的无人艇艏向和舵角响应情况。从图8中可以观察出,即使期望航向是时变量,实际航向扔能在舵角控制律的作用下较为理想地达到期望值。艏向在70 s和110 s时间附近存在阶跃情况,原因是在仿真中为了符合实际情况,设置了船舶的艏向角范围为(-180°, 180°]。为使船体在持续环境扰动下仍能保持艏向的稳定性,舵角存在持续性的低频扰动补偿,如图9所示。

图8 艏向时间曲线

图9 舵角时间曲线
综合图5~图9的仿真结果可知,在式(3)推力-转速函数及式(12)、式(21)推力与舵角控制律的联合作用下,能够有效地实现对带有控制力约束的喷水推进船的鲁棒运动控制。
5 结论
本文通过拟合分析的方式,设计得出喷水推力关于主机转速和船舶航速的函数关系式,所得函数具有形式简单易于计算的优点。通过与原始推力图谱对比,拟合函数的推力估计误差小于3.61%,能够满足运动控制的精度需求。在此基础上开展了喷水推进船航速与航向鲁棒控制律设计,控制器设计过程中充分考虑到了控制机构的约束条件,将控制律落脚到主机转速和舵角的具体控制分配层,完成了对喷水推进船的全过程控制。通过一个指定航速下的路径跟踪仿真试验,验证了本文控制方法在应对推力不确定和外界扰动时,同时进行航速与航向鲁棒控制的可行性。
