基于改进ESMD的轴承故障诊断
2022-01-21高志彬
张 明,高志彬
(1. 潍坊工程职业学院,山东潍坊 262500;2. 青岛理工大学,山东青岛 266033)
0 引言
轴承是机械设备常用的零部件设备,能够承受载荷支撑机械旋转体,有效地降低摩擦载荷系数,保证旋转机械的回转精度。轴承运行转速高、载荷大的特点使其极易发生疲劳剥落或点蚀,进而导致轴承失效。相关统计数据表明:含轴承类部件的故障30%与轴承缺陷有关[1],轴承部件故障影响汽车正常行驶,造成经济损失和安全问题,因此轴承故障检测有重要意义,而从轴承振动波中提取出故障特征是故障诊断的关键。
1 轴承故障诊断方法
1.1 轴承振动波
轴承结构体受振源激励产生有清晰物理意义的振动波,通过测取轴承的状态信息,分析运行状态信息,结合故障特征信息识别轴承实时技术转态,识别异常故障并预测异常发展趋势,进而制定合理的维护策略。振动波形易于测量,受外界干扰小,能够有效提取轴承初期的故障特征,轴承故障表现为时域波形振幅显著增大的周期性脉冲波,频谱中包含有故障脉冲频率。
1.2 信号处理方法
利用短时傅立叶变换(Short-Time Fourier Transform,DFFT)和威格纳维尔(WV)分布等时频域分析方法,可以分析非平稳信号性质并在轴承故障检测方面得到应用[2]。由于DFFT仅使用小部分数据分析,因此在处理时变信号时其多分辨率解决方案是有限的[3]。应用WV变换的困难在于卷积运算会在信号中加入交叉项[4],从而影响信号处理精度。ESMD是王金良等[5]在海洋学领域提出的数据处理方法,无需预先取定基函数或窗口长度,所分离出的有限个模态其频率和振幅都是可变的,是数据自适应处理方式,极值点在振动波形中有标志性作用,从而更好地对应物理实际固有振型,在处理非线性、非稳态信号方面有很大的优势。ESMD涉及本征模态分量分解和希尔伯特谱分析,首先将信号分解成一系列不同尺度的数据序列,称为本征模态分量,而后对其进行希尔伯特变换计算瞬时频率。
2 ESMD 的改进
2.1 波形平衡线
模态迭代(分解)过程是为获取表示实际物理振动形式的幅变或幅频调制波形,振幅变化是由外界空气阻尼和激励引起的,而频率变化则是因为平衡点位置的移动所造成,波形平衡位置调整是在分解过程中模态分量间的相互干扰作用所造成。
模态分解迭代过程中极值点拟合外包络线存在不能很好贴合信号的过包络现象,以及切割信号的欠包络现象[6],由此产生的包络均值线误差随着模态分解过程传递积累,改进ESMD的包络线是由波形内部极值中点插值形成,避免上述问题。多项式次幂的升高能够表示复杂函数关系,但拟合函数表达式不利于问题分析与求解[7],在满足需求的前提下应用低次多项式表示相邻数据区间的物理实际关系,为降低插值运算量,应用更加快速的波形平衡线构造方式,进一步查找相邻两极值中点间的等距点,为方便描述将此点命名为“高阶极值中点”,以轴承振动波形中的普遍性情形解释,两相邻极值中点是高低间错排布,两极值中点不相等且不存在3个及以上相邻极值点递增或递减情形,使用线段依次连接各相邻极值中点构造的随机波形近似于原始波动平衡位置,高阶极值中点是在随机波形中再次查找波形平衡位置,由此构造波形平衡线达到最佳时去除该波形视为原始信号脉动量[8]。
2.2 模态分解过程
振动波的包络线满足极点对称,多个相邻的等幅值极点视为一个极值点,极大值点与极小值点间错排布[9]。模态分解过程如下:
1)寻找原始信号数据所有极大值点和所有极小值点,利用线段依次连接两相邻的极值点,即一组极大值点和极小值点,形成锯齿状的折线图,取所有线段中点得到极值中点。
2)原始波形的线段中点为基础,进一步查找高阶极值中点,并以初始和末端多个高阶极值中点平均值补充两端边界点,拟合由边界点和高阶极值中点组成的数据集,构造波形平衡线。
3)原始波形去除均值曲线获取新的振动波形,判断迭代后的波形是否满足本征模态分量定义条件[10],若满足则标记为首个经验模态;若不满足则对新的波形重复上述两步直到满足定义条件。依次获得剩余本征模态分量和余量,最后的余量仅包含有限数量的极值点。
3 试验验证
轴承振动波来自CWRU轴承试验室公开数据,轴承运行转速为1 797 r/min且无负载,外环缺陷和内环缺陷尺寸(面积深度)约为0.178 mm。采用驱动端试验数据,采样点数3 000,采样频率为轴承旋转周期12 kHz,验证改进ESMD在轴承故障诊断过程的有效性,仅对包含主要故障信息的初始模态分量分析实现快速诊断,所有分析过程在Matlab中实现。
3.1 正常轴承
正常轴承的时域波形如图1所示,振动波没有明显的冲击波形,整体变化平稳,振动幅值集中在-0.30~0.25 m/s2。

图1 正常轴承时域波形
3.2 内环故障轴承
轴承内环故障振动波进行模态分解,初始模态分量时域波形图2所示,幅值主要分布在-0.5~0.6 m/s2,比正常轴承振动波形幅值高。

图2 内环故障IMF时域波形
按照故障特征频率计算公式[11]得出内环故障频率是162 Hz。因为轴承系统并非简单的纯滚动运动,对实际振动波处理时,振动波频谱的峰值有时在数值上并不精确等于理论计算值[12]。轴承内环故障振动波形初始模态分量进行希尔伯特变换,包络谱如图3所示故障特征频率162 Hz,并提取到首个模态分量中的多倍故障频率特征。
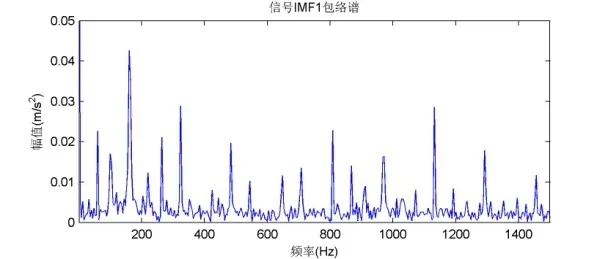
图3 内环故障IMF HT包络谱
3.3 外环故障轴承
轴承外环故障振动波进行模态分解,由图4可知轴承外环故障振动波形初始模态分量中存在故障脉冲信号,振幅值-2.0~2.5 m/s2远高于正常轴承。

图4 外环故障IMF时域波形
外环故障轴承的特征频是107 Hz,同样振动波频谱峰值和理论计算值存在微小误差。轴承外环故障振动波形初始模态分量的希尔伯特谱图5存在外环故障特征频率108 Hz,这与理论值十分接近,同时还可以清晰看出多倍故障特征频率。

图5 外环故障IMF HT包络谱
4 结论
本文针对轴承运行中振动波特性,从极点对称模态分解方法出发,对模态分解过程进行改进。将改进后的ESMD应用到轴承内环和外环故障诊断,可快速有效地分解出振动波形信号中的本征模态分量。然而,在改进ESMD的数学证明有待更深入的研究,从鲁棒性分析和理论依据做详细探讨,完善极点对称模态分解方法的理论体系。
